Zagadnienia
14. Przepływy w sieciach
14.1. Przepływy w sieciach.
Siecią nazywać będziemy skończony graf ![]() wraz z dwiema funkcjami
wraz z dwiema funkcjami ![]() przypisującą każdemu wierzchołkowi liczbę rzeczywistą
przypisującą każdemu wierzchołkowi liczbę rzeczywistą ![]() zwaną potencjałem i
zwaną potencjałem i ![]() przypisującą każdej krawędzi koszt przepływu. Ponieważ zawiera wierzchołki i krawędzie więc, dla uniknięcia nieporozumień, wierzchołki sieci będziemy nazywać węzłami zaś zorientowane krawędzie strzałkami.
przypisującą każdej krawędzi koszt przepływu. Ponieważ zawiera wierzchołki i krawędzie więc, dla uniknięcia nieporozumień, wierzchołki sieci będziemy nazywać węzłami zaś zorientowane krawędzie strzałkami.
Zagadnienie przepływy w sieciach ( o nieograniczonej przepustowości ) polega na znalezieniu schematu przepływu o minimalnych kosztach, wyrównującego potencjały.
Modelem matematycznym takiego zagadnienia będzie:
Jako zmienne wybieramy zbiór ![]() indeksowany strzałkami grafu.
indeksowany strzałkami grafu.
![]() na obszarze opisanym nierównościami:
na obszarze opisanym nierównościami:
![]()
![]() .
.
Zauważmy, macierz opisująca powyższe równania ma wiersze indeksowane węzłami a kolumny, z prawej strony kreski, indeksowane strzałkami ![]() (lub zmiennymi
(lub zmiennymi ![]() ). Ponadto kolumna odpowiadająca strzałce
). Ponadto kolumna odpowiadająca strzałce ![]() ma zera, jedną 1 w wierszu o indeksie
ma zera, jedną 1 w wierszu o indeksie ![]() i jedną -1 w wierszu o indeksie
i jedną -1 w wierszu o indeksie ![]() . W przypadku grafu ukorzenionego strzałką
. W przypadku grafu ukorzenionego strzałką ![]() , dochodzi kolumna o indeksie
, dochodzi kolumna o indeksie ![]() , która ma zera i jedną 1 w wierszu o indeksie
, która ma zera i jedną 1 w wierszu o indeksie ![]()
Jak zsumujemy wszystkie równania, dla grafu nieukorzenionego, lewa strona zredukuje się do 0 i otrzymamy:
![]()
A zatem ten układ równań jest zależny i jeżeli suma potencjałów jest niezerowa to jest sprzeczny. Zagadnienie gdy ![]() nazywamy zrównoważonym.
nazywamy zrównoważonym.
Zajmijmy się teraz zrównoważonym zadaniem przepływu w sieci, która jest grafem spójnym. Okazuje się, że w takim przypadku po ukorzenieniu grafu w dowolnym wierzchołku równania stają się liniowo niezależne a każdy układ bazowy jest wyznaczony przez pewne drzewo spinające. Dokładniej.
Twierdzenie 14.1
Niech ![]() będzie spójnym grafem ukorzenionym w węźle
będzie spójnym grafem ukorzenionym w węźle ![]() wraz z funkcjami potencjału
wraz z funkcjami potencjału ![]() i kosztów
i kosztów ![]() takimi, że
takimi, że ![]() . Wówczas:
. Wówczas:
a) Zbiór równań ![]() jest liniowo niezależny.
jest liniowo niezależny.
b) Jeżeli kolumny o indeksach ![]() są liniowo niezależne i
są liniowo niezależne i ![]() to podgraf
to podgraf ![]() , gdzie
, gdzie ![]() jest ukorzenionym drzewem spinającym.
jest ukorzenionym drzewem spinającym.
Twierdzenie 14.1 w dalszej części będziemy używać poprzez następujący wniosek.
Wniosek 14.1
Niech TS będzie tablicą sympleks opisującą zagadnienie przepływu w sieci spójnej. Wówczas graf powstały przez odrzucenie strzałki indeksujących zmienne niebazowe jest drzewem spinającym.
Do dowodu części b) twierdzenia 14.1 użyjemy następującego lematu.
Lemat 14.1
Niech ![]() przebiegający między wierzchołkami
przebiegający między wierzchołkami
![]() będzie cyklem prostym w sieci
będzie cyklem prostym w sieci ![]() . Wówczas kolumny
. Wówczas kolumny ![]() tablicy sympleks indeksowane tymi krawędziami są liniowo zależne.
tablicy sympleks indeksowane tymi krawędziami są liniowo zależne.
Dowód lematu. Wprowadźmy orientację na cyklu ![]() zgodną z kolejnością węzłów
zgodną z kolejnością węzłów ![]() . To znaczy: Niech strzałka przebiega między węzłami
. To znaczy: Niech strzałka przebiega między węzłami ![]() i
i ![]() , definiujemy
, definiujemy ![]()
Badamy kolumnę ![]() .
.
W j - tym wierszu kolumny ![]() (w wierszu indeksowanym węzłem
(w wierszu indeksowanym węzłem ![]() ) występuje element
) występuje element
![e_{{i,j}}=\left\{\begin{array}[]{rl}1&,p(s_{i})=w_{j}\\
-1&,k(s_{i})=w_{j}\\
0&,p(s_{i})\neq w_{j}\neq k(s_{i})\end{array}\right.=\left\{\begin{array}[]{rl}1&,p(s_{i})=w_{j}\\
-1&,p(s_{i})=w_{{j-1}}\\
0&,p(s_{i})\neq w_{j}\neq k(s_{i})\end{array}\right.](wyklady/op1/mi/mi1554.png)
![e_{{i,j}}=\left\{\begin{array}[]{rl}-\varepsilon _{i}&,i=j\\
\varepsilon _{i}&,i=j+1\\
0&,j\neq i\neq j+1\end{array}\right.](wyklady/op1/mi/mi1542.png)
Zatem w j - tym wierszu kolumny ![]() występuje
występuje ![]() lub
lub ![]() .
.
Dowód twierdzenia.
a) Wybieramy dowolne drzewo spinające ![]() , ukorzenione. Macierz układu równań opisujących obszar dopuszczalny zadany drzewem jest podmacierzą wyjściowego układu więc do wykazania liniowej niezależności możemy przyjąć, że graf jest drzewem spinającym. Dowód przeprowadzimy przez indukcję względem liczby węzłów.
, ukorzenione. Macierz układu równań opisujących obszar dopuszczalny zadany drzewem jest podmacierzą wyjściowego układu więc do wykazania liniowej niezależności możemy przyjąć, że graf jest drzewem spinającym. Dowód przeprowadzimy przez indukcję względem liczby węzłów.
![]() Sieć ma 1 wierzchołek i 1 krawędź wychodzącą z niego. Zatem macierzą układu jest
Sieć ma 1 wierzchołek i 1 krawędź wychodzącą z niego. Zatem macierzą układu jest ![]() o maksymalnym rzędzie.
o maksymalnym rzędzie.
![]() Jeżeli sieć ma co najmniej dwa węzły to ma liść
Jeżeli sieć ma co najmniej dwa węzły to ma liść ![]() , który nie jest korzeniem. Usuwamy liść
, który nie jest korzeniem. Usuwamy liść ![]() i strzałkę
i strzałkę ![]() z nim związaną. Zobaczmy jak zmienia się macierz M układu równań. Wiersz indeksowany liściem
z nim związaną. Zobaczmy jak zmienia się macierz M układu równań. Wiersz indeksowany liściem ![]() ma tylko jedno miejsce różne od 0 -
ma tylko jedno miejsce różne od 0 -![]() w kolumnie o indeksie
w kolumnie o indeksie ![]() . Zatem po usunięciu tego wiersza i kolumny rząd macierzy maleje o 1.
. Zatem po usunięciu tego wiersza i kolumny rząd macierzy maleje o 1.
ad b) Po odrzuceniu korzenia otrzymujemy podsieć ![]() o
o ![]() węzłach i
węzłach i ![]() strzałkach, nie mający cykli. A taka sieć jest drzewem.
strzałkach, nie mający cykli. A taka sieć jest drzewem.
Algorytm sympleks w sieciach.
Algorytm ten będziemy ilustrować przykładem.
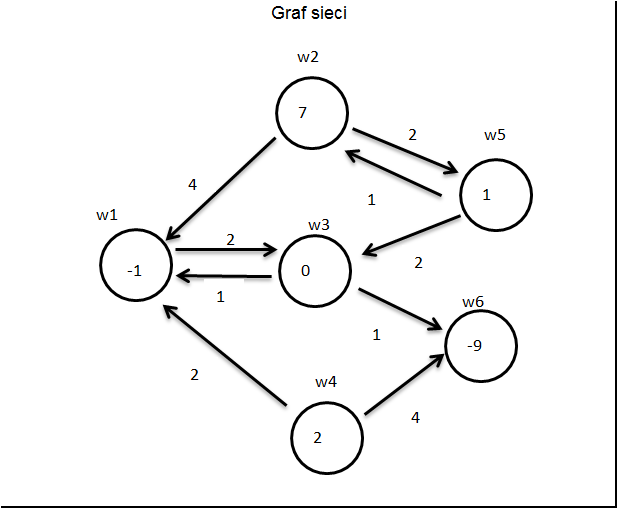
Dane zadanie opisane grafem
Liczby w węzłach opisują potencjały zaś na strzałkach koszty.
Jak widać suma potencjałów jest zerowa więc zadanie jest zbilansowane.
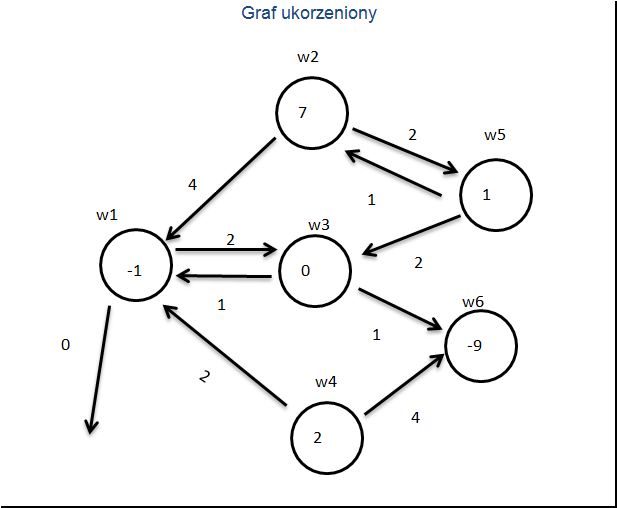
Ukorzeniamy graf w węźle ![]() .
.
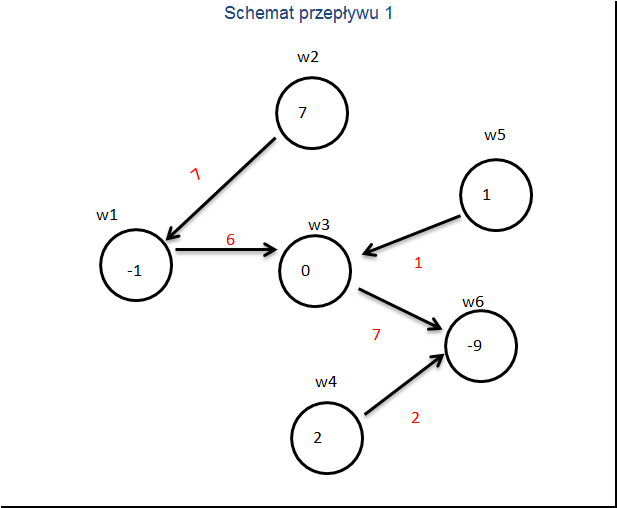
Do rozpoczęcia algorytmu potrzebujemy wierzchołek startowy. Niech będzie nim następujące drzewo spinające:
Czerwone liczby oznaczają wartości zmiennych czyli liczba towaru przepływająca przez strzałkę.
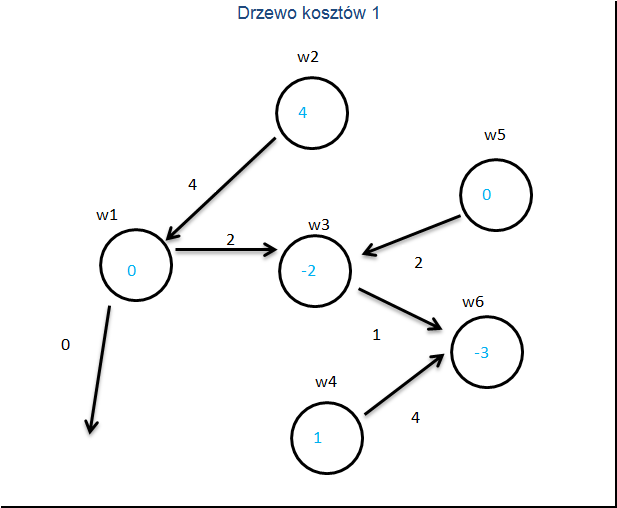
Krok 1 TEST OPTYMALNOŚCI
Budujemy pomocnicze drzewo kosztów. Koszty podróży po strzałkach są te same a liczby w węzłach obrazują koszt spływu jednostki towaru przez korzeń. W przypadku podróży pod prąd koszt strzałki liczymy ze znakiem minus.
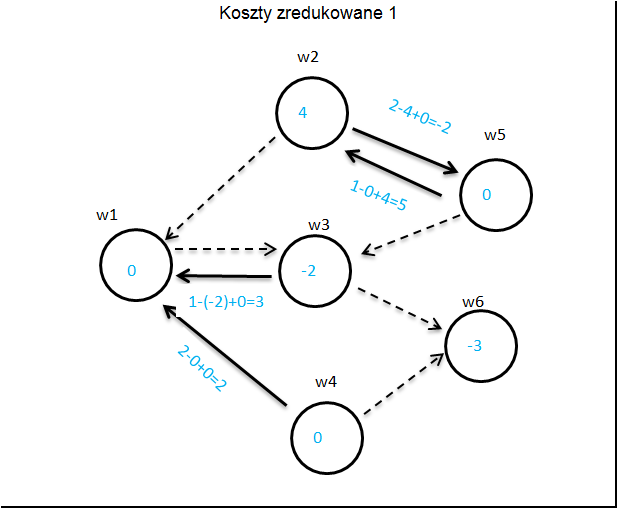
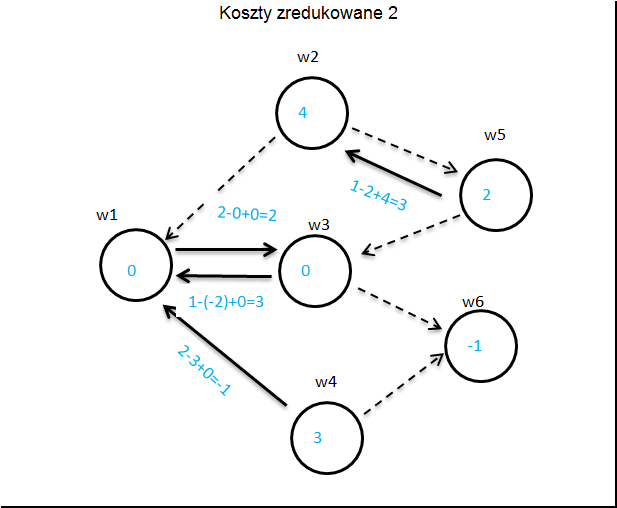
Teraz wyliczamy koszty zredukowane.
Liczymy koszty zredukowane zgodnie z zasadą: Na węźle ![]() umieszczamy liczbę
umieszczamy liczbę ![]() z drzewa kosztów. Następnie koszt każdej strzałki wychodzącej z
z drzewa kosztów. Następnie koszt każdej strzałki wychodzącej z ![]() zmniejszamy o
zmniejszamy o ![]() zaś koszt każdej strzałki przychodzącej do
zaś koszt każdej strzałki przychodzącej do ![]() zwiększamy o
zwiększamy o ![]() . Wartość funkcji celu zmieni się przy tej ope4racji o stałą
. Wartość funkcji celu zmieni się przy tej ope4racji o stałą ![]() . Metoda obliczania wartości węzłów w drzewie kosztów wymusza zerowe koszty strzałek użytych w schemacie przepływu ( zerowe koszty zmiennych bazowych ).
. Metoda obliczania wartości węzłów w drzewie kosztów wymusza zerowe koszty strzałek użytych w schemacie przepływu ( zerowe koszty zmiennych bazowych ).
Koszt zredukowany strzałki ![]() między węzłami
między węzłami ![]() a
a![]() wynosi
wynosi ![]() .
.
Jeżeli wszystkie strzałki mają koszt nieujemny to STOP badany schemat jest optymalny.
Krok 2. WYBÓR KOLUMNY POPRAWIAJĄCEJ
Wybieramy teraz strzałkę o ujemnym koszcie i dołączamy ją do drzewa. W naszym przykładzie jest to strzałka zaznaczona linią przerywaną z ![]() do
do ![]() .
.
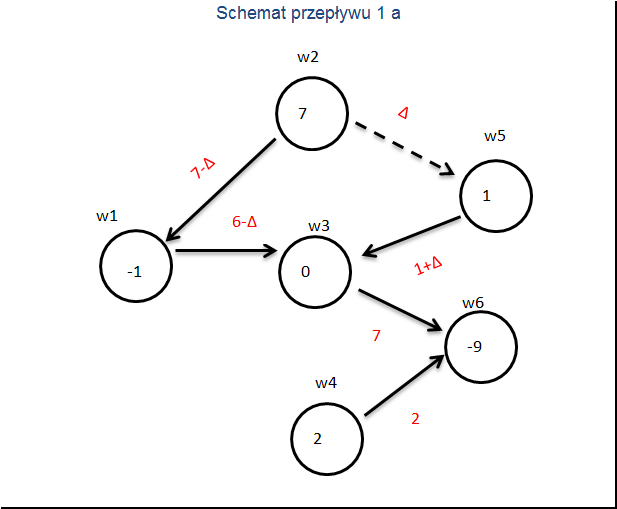
Krok 3. WYBÓR ELEMENTU CENTRALNEGO
Pojawia się cykl po którym staramy się przepchnąć jak najwięcej towaru. Dołączoną strzałką podróżuje ![]() jednostek a pozostałymi strzałkami o
jednostek a pozostałymi strzałkami o ![]() mniej lub więcej w zależności od ich zwrotu.
Ponieważ zmienne są nieujemne jako
mniej lub więcej w zależności od ich zwrotu.
Ponieważ zmienne są nieujemne jako ![]() wybieramy minimum z kosztów strzałek przeciwnie zorientowanych niż dodana. W naszym przykładzie
wybieramy minimum z kosztów strzałek przeciwnie zorientowanych niż dodana. W naszym przykładzie ![]() .
.
Teraz z grafu wyrzucamy jedną ze strzałek po której nie płynie towar. W naszym przykładzie jest to strzałka z ![]() do
do ![]() . W ten sposób otrzymaliśmy nowy schemat przewozu, który jest drzewem a więc wierzchołkiem obszaru dopuszczalnego. Funkcję celu poprawiliśmy o
. W ten sposób otrzymaliśmy nowy schemat przewozu, który jest drzewem a więc wierzchołkiem obszaru dopuszczalnego. Funkcję celu poprawiliśmy o ![]() pomnożone przez koszt dołączonej strzałki. W naszym przykładzie wyrzucamy strzałkę z
pomnożone przez koszt dołączonej strzałki. W naszym przykładzie wyrzucamy strzałkę z ![]() do
do ![]() .
.
GO TO krok 1
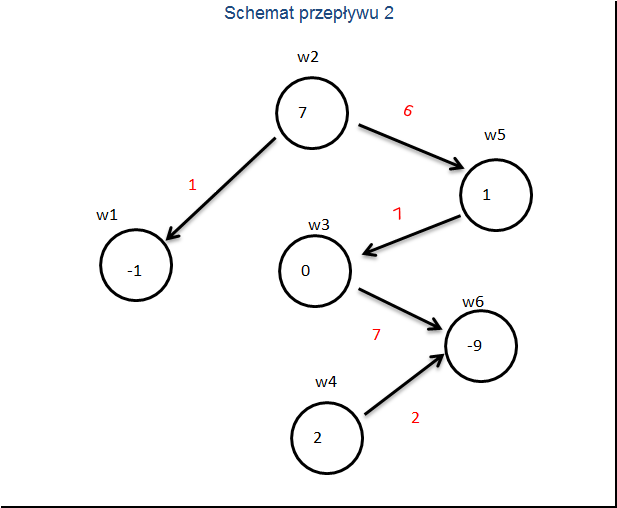
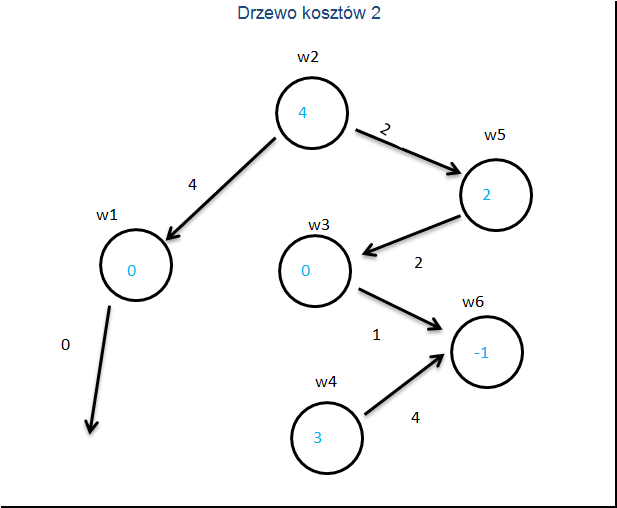
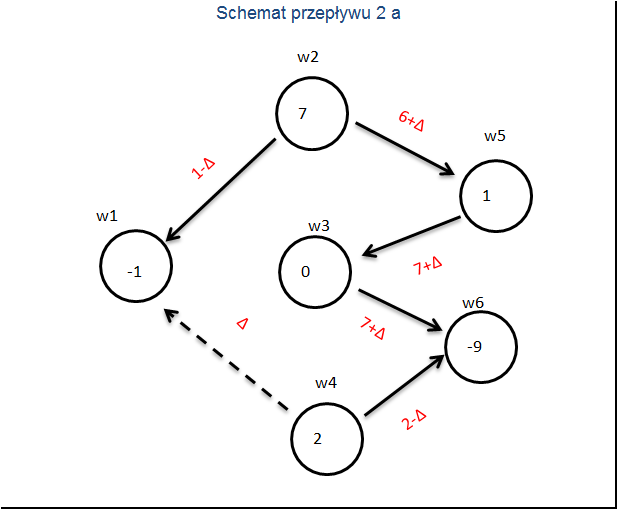
Budujemy drugie drzewo kosztów.
i wyliczamy koszty zredukowane drugiego schematu przepływu.
Tym razem ujemny koszt ma strzałka z ![]() do
do ![]() . Dołączamy ją i otrzymujemy cykl:
. Dołączamy ją i otrzymujemy cykl:
W naszym przykładzie ![]() więc wyrzucamy strzałkę z
więc wyrzucamy strzałkę z ![]() do
do ![]() . Otrzymujemy trzeci schemat przepływu.
. Otrzymujemy trzeci schemat przepływu.
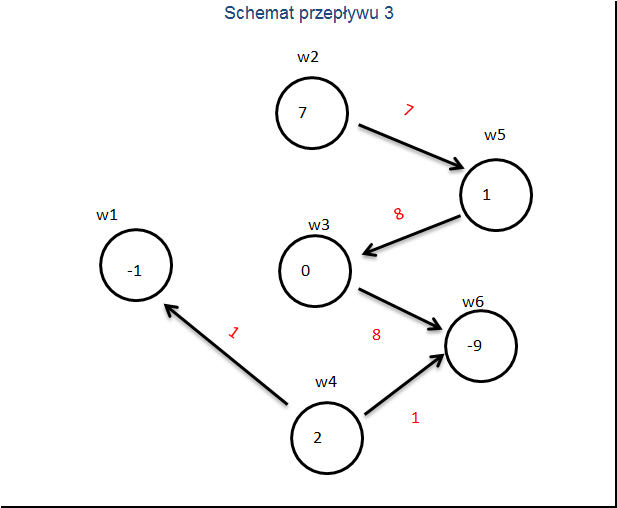
Znowu liczymy koszty zredukowane.
[0.5]KZ3Koszty zredukowane 3
Są one nieujemne więc schemat trzeci jest optymalny.
Dwufazowa metod sympleks.
Dana jest sieć ![]() wraz z potencjałem
wraz z potencjałem ![]() . Wprowadzamy dodatkowy (sztuczny ) węzeł o potencjale 0 i strzałki łączące sztuczny węzeł ze wszystkimi pozostałymi tak skierowane by potencjały mogły się wyrównać. Następnie wprowadzamy sztuczną funkcję celu nadając starym strzałkom koszt 0 a sztucznym koszt 1. Dalej stosujemy prosty algorytm sympleks. Jeżeli nie uda się uzyskać przepływu o koszcie 0 to znaczy, że wyjściowe zadanie jest sprzeczne. W przeciwnym przypadku uzyskamy przepływ będący wierzchołkiem obszaru dopuszczalnego.
. Wprowadzamy dodatkowy (sztuczny ) węzeł o potencjale 0 i strzałki łączące sztuczny węzeł ze wszystkimi pozostałymi tak skierowane by potencjały mogły się wyrównać. Następnie wprowadzamy sztuczną funkcję celu nadając starym strzałkom koszt 0 a sztucznym koszt 1. Dalej stosujemy prosty algorytm sympleks. Jeżeli nie uda się uzyskać przepływu o koszcie 0 to znaczy, że wyjściowe zadanie jest sprzeczne. W przeciwnym przypadku uzyskamy przepływ będący wierzchołkiem obszaru dopuszczalnego.
Przypadek niezbilansowany.
Przypadek niezbilansowany sprowadzamy do zbilansowanego wprowadzając sztuczny węzeł o potencjale przeciwnym do sumy pozostałych potencjałów i strzałki łączące sztuczny węzeł ze wszystkimi pozostałymi. Jeżeli sztuczny węzeł ma potencjał dodatni to wszystkie sztuczne strzałki z niego wychodzą. Jeżeli ujemny to wszystkie sztuczne strzałki mają w nim swój koniec. Dalej stosujemy prosty algorytm sympleks.
Ćwiczenie 14.1
W sieci o strzałkach z nieograniczonymi przepustowościami aktualnie realizowany jest następujący schemat przepływów:
[0.5]ZadPSchemat przepływu
Wyznacz przepływ o minimalnym koszcie za pomocą algorytmu sympleks.
Przykład i zadanie w tym wykładzie pochodzą z egzaminów prof. W. Ogryczaka.
![\begin{figure}[!ht] \ffig[]{}{}{} \caption{.} \end{figure}](wyklady/op1/dk3.png)
![\begin{figure}[!ht] \ffig[]{}{}{} \caption{.} \end{figure}](wyklady/op1/ZadGraf.png)




