Zagadnienia

3.1 Wierzchołki i krawędzie
- Zadania

3. Wierzchołki i krawędzie

3.1. Wierzchołki i krawędzie

Definicja 3.1

Niech $T\in\mathbb{R}^{{n}}$ będzie niepustym podzbiorem. Relatywnym wnętrzem zbioru $T$ nazywamy podzbiór $rint(T)=\{ p\in T\,|\,\exists _{{\varepsilon>0}}\, K(p,\varepsilon)\cap af(T)\subset T\}$ .

Pojęcie relatywnego wnętrza jest praktyczniejsze przy badaniu wielościanów niż zwykłe wnętrze. Np. relatywnym wnętrzem odcinka w przestrzeni trójwymiarowej jest odcinek otwarty mimo, że cały odcinek jest brzegiem.

Stwierdzenie 3.1

Jeżeli $T$ jest niepustym podzbiorem wypukłym w $\mathbb{R}^{n}$ to $rint(T)\neq\emptyset$ .

Dowód zostawiamy czytelnikowi.

Zajmijmy się kluczowym lematem przy opisie ścian wielościanu.

Lemat 3.1

Niech $p$ będzie punktem wielościanu

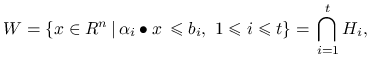$W=\left\{ x\in R^{{n}}\,|\,\alpha _{{i}}\bullet x\,\leq b_{{i}},\ 1\leq i\leq t\right\}=\bigcap _{{\, i=1}}^{{\, t}}H_{i},$

gdzie $H_{i}=\left\{ x\in R^{{n}}\,|\,\alpha _{{i}}\bullet x\,\leq b_{{i}}\right\} S$ są półprzestrzeniami.

Dodatkowo zakładamy, że nierówności są tak ustawione by:

$\alpha _{{i}}\bullet p\,=b_{{i}}$ dla $1\leq i\leq s$ ;

$\alpha _{{i}}\bullet p\,<b_{{i}}$ dla $s<i\leq t$ ;

Oznaczmy literą $j$ liczbę $n-rz\, A_{p}$ czyli wymiar przestrzeni rozwiązań układu jednorodnego opisanego macierzą $A_{p}$ ,

gdzie $A_{p}=\left[\begin{array}[]{c}\alpha _{{1}}\\ \alpha _{{2}}\\ ...\\ \alpha _{{s}}\end{array}\right]$ , jest podmacierzą macierzy opisującej W złożoną z pierwszych s wierszy macierzy opisującej $W$ .

Wówczas:

1) $S=W\cap\ \bigcap\limits _{{i\leq s}}H_{i}^{-}$ jest ścianą wymiaru $j$ , zaś punkt $p$ należy do jej relatywnego wnętrza.

2) Punkt p jest środkiem pewnej j - wymiarowej kuli zawartej w W.

3) Punkt p nie jest środkiem żadnej kuli $j+1$ - wymiarowej zawartej w W.

Niech $V$ będzie zbiorem rozwiązań układu $V=\left\{ x\in R^{{n}}\,|\,\alpha _{{i}}\bullet x\,=b_{{i}},\ 1\leq i\leq s\right\}.$ Ponieważ $p\in V$ i $V$ jest zbiorem rozwiązań układu równań liniowych więc na mocy twierdzenia Kroneckera - Capelli'ego $V$ jest przestrzenią afiniczną wymiaru $n-rz(A_{p})=j$ . Zauważmy dodatkowo $V=\bigcap\limits _{{i\leq s}}H_{i}\ \cap\ \bigcap\limits _{{i\leq s}}H_{i}^{-}$ .

Niech $S_{i}=W\cap\partial H_{i}$ . Wówczas dla $1\leq i\leq s\ S_{i}$ są ścianami $W$ zawierającymi punkt $p$ zatem na mocy lematu 2.1 $S$ jest ścianą wielościanu $W$ . Ponadto $S=W\cap\ \bigcap\limits _{{i\leq s}}H_{i}^{-}=\bigcap\limits _{{i\leq t}}H_{i}\ \cap\ \bigcap\limits _{{i\leq s}}H_{i}^{-}\subset\bigcap\limits _{{i\leq s}}H_{i}\ \cap\ \bigcap\limits _{{i\leq s}}H_{i}^{-}=V$ więc $dim\, S\leq j$ .

Aby wykazać, że $dim\, S=j$ i $p\in rint\, S$ znajdziemy $j-$ wymiarową kulę, zawartą w $S$ o środku w punkcie $p$ .

Niech $\varepsilon _{i}=\rho(p\,;\partial H_{i})$ będzie odległością punktu $p$ od brzegu odpowiedniej półprzestrzeni. Niech $\varepsilon=Min\{\varepsilon _{i}\,|\, s<i\leq t\}$ . Teraz $K=K(p\,;\varepsilon)\cap V\subset W\cap V=S$ jest $j-$ wymiarową kulą o środku $p$ .

Niech $B$ będzie kulą o środku $p$ zawartą w wielościanie $W$ . Wtedy $\forall _{{i\leq s}}B\subset H_{i}$ oraz $p\in\partial H_{i}$ . Na mocy lematu 2.2 $B\subset\bigcap\limits _{{i\leq s}}\,\partial H_{i}=V$ . Stąd $dim\ B\leq j$ .

∎

Stwierdzenie 3.2

Niech $S=W\cap\partial H$ będzie ścianą wielościanu $W$ . Wówczas $S=W\,\cap\ af(S)$ .

Inkluzja $S\subset W\cap af(S)$ jest oczywista.

Ponieważ $S\subset\partial H$ i $\partial H$ jest podprzestrzenią, więc $af(S)\subset\partial H$ . Stąd $W\cap af(S)\subset W\cap\partial H=S$ .

∎

Lemat 3.2

Niech S będzie ścianą wielościanu $W$ , zaś p jej punktem relatywnie wewnętrznym. Wówczas $S=W\cap af\left(K\right)$ , gdzie $K\subset W$ jest kulą o środku w punkcie $p$ , maksymalnego wymiaru.

Niech $S=W\cap\partial H$ . Ponieważ $p\in\partial H$ , więc $K\subset W\cap\partial H=S$ . Stąd $af(S)=af(K)$ i $S=W\cap af(S)=W\cap af(K)$ .

∎

Lemat 3.3

Niech S będzie ścianą wielościanu $W=\bigcap _{{\, i=1}}^{{\, t}}\, H_{i}$ , zaś p jej punktem relatywnie wewnętrznym.

Wówczas $S=W\,\cap\bigcap\limits _{{\{ i|p\in\partial H_{i}\}}}\partial H_{i}=W\,\cap\bigcap\limits _{{\{ i|p\in H_{i}^{-}\}}}\ H_{i}^{-}$ .

Niech $S=W\cap\partial H$ , dla pewnej półprzestrzeni $H\supset W$ . Wówczas

$W=H\cap\bigcap _{{\, i=1}}^{{\, t}}\ H_{i}$ i z dowodu poprzedniego lematu

$S=W\cap\partial H\ \cap\ \bigcap\limits _{{p\in\partial H_{i}}}\ \partial H_{i}\ \subset W\cap\ \bigcap\limits _{{p\in\partial H_{i}}}\partial H_{i}=\overline{S}$ . Do dowodu $S=\overline{S}$ wystarczy zauważyć, że $S$ jest ścianą tego samego wymiaru co $\overline{S}$ , gdyż każda kula o środku w $p$ zawarta w $\overline{S}$ jest zawarta w $S$ .

∎

Lemat 3.4

Niech $W=\bigcap _{{\ i=1}}^{{\ t}}H_{i}\ \subset\mathbb{R}^{n}$ będzie wielościanem.

Jeżeli $W\neq\bigcap _{{\ i=2}}^{{\ t}}H_{i}$ to $W\cap\partial H_{1}\neq\emptyset$ .

Niech $q\in\bigcap _{{i=2}}^{t}H_{i}\setminus W$ zaś $p\in W$ . Oznaczmy przez $q^{{\prime}}$ punkt przecięcia odcinka $\overline{p\ q}$ z $\partial H_{1}$ . Punkty $p$ oraz $q$ leżą po różnych stronach hiperpłaszczyzny $\partial H_{1}$ więc punkt przecięcia odcinka $\overline{p_{i}\ q}$ z $\partial H_{1}$ należy do $W$ .

∎

Lemat 3.5

Niech $W\in\mathbb{R}^{n}$ będzie wielościanem. Wówczas $W$ jest podprzestrzenią afiniczną wtedy i tylko wtedy gdy $W$ nie ma właściwych ścian ( to znaczy ścian różnych od $W$ ).

$\Rightarrow$ Niech $W$ będzie przestrzenią afiniczną zaś $S=W\cap\partial H$ ścianą. Wybierzmy dowolny punkt $p\in S$ . Ponieważ $p\in\ rint\, W$ więc istnieje kula $K$ o środku w punkcie $p$ rozpinająca $W$ . Ale na mocy lematu 1.1 $K\subset\partial H$ więc $W=af(K)\subset\partial H$ i $W=S$ .

$\Leftarrow$

a) Jeżeli $W=\mathbb{R}^{n}$ to jest podprzestrzenią afiniczną.

b) Niech $W=\bigcap _{{\, i=1}}^{{\, t}}H_{i}$ będzie opisem wielościanu $W$ przy pomocy minimalnego zbioru półprzestrzeni. Na mocy lematu 3.4 zbiór $S_{i}=W\cap\partial H_{i}\neq\emptyset$ dla każdego $1\leq i\leq t$ . Zatem są to ściany oraz $W=S_{i}\subset\partial H_{j}$ . Otrzymujemy $W\subset\bigcap _{{i=1}}^{t}\,\partial H_{i}\subset\bigcap _{{i=1}}^{t}\, H_{i}=W$ . Stąd $W=\bigcap _{{i=1}}^{t}\,\partial H_{i}$ jest podprzestrzenią afiniczną.

∎

Bezpośrednio z wniosku 2.1 i lematu 3.2 otrzymujemy:

Twierdzenie 3.1

Niech $W=\bigcap _{{\, i=1}}^{{\, t}}\ H_{i}\ \subset\mathbb{R}^{n}$ będzie wielościanem zaś T podzbiorem $\{ 1,2,3,...,t\}$ . Wówczas

1) $S=\bigcap _{{\, i=1}}^{{\, t}}\ H_{i}\cap\bigcap _{{i\in T}}\ H_{i}^{-}$ jest ścianą lub zbiorem pustym.

2) Każda ściana S wielościanu W jest postaci $S=\bigcap _{{\, i=1}}^{{\, t}}\ H_{i}\cap\bigcap\limits _{{\{ i\,|\, p\in H_{i}\}}}\, H_{i}^{-}$ , gdzie $p$ jest dowolnie ustalonym punktem relatywnego wnętrza S.

Wniosek 3.1

Ściana ściany wielościanu jest ścianą.

Popatrzmy jak poprzednie lematy można zastosować do opisu wierzchołków.

Twierdzenie 3.2

Niech $p$ będzie punktem wielościanu $W\subset R^{n}$ , opisanego układem

$\left\{ x\in R^{{n}}:\begin{array}[]{c}\alpha _{{1}}\bullet x\,\leq b_{{1}}\\ \alpha _{{2}}\bullet x\,\leq b_{{2}}\\ \cdots\\ \alpha _{{t}}\bullet x\,\leq b_{{t}}\end{array}\right.$ .

Dodatkowo zakładamy, że równania są tak ustawione by:

$\alpha _{{i}}\bullet p\,=b_{{i}}$ dla $1\leq i\leq s$ ;

$\alpha _{{i}}\bullet p\,<b_{{i}}$ dla $s<i\leq t$ ;

Wówczas równoważne są warunki:

1) $p$ jest wierzchołkiem wielościanu $W$ .

2) $p$ nie jest środkiem odcinka zawartego w W.

2a) $p$ nie jest nietrywialną kombinacją wypukłą punktów z $W$ .

3) rząd macierzy $A_{p}=n$ gdzie $A_{p}=\left[\begin{array}[]{c}\alpha _{{1}}\\ \alpha _{{2}}\\ ...\\ \alpha _{{s}}\end{array}\right]$ , jest podmacierzą macierzy opisującej W złożoną z pierwszych s wierszy tej macierzy.

Implikacje $1)\Rightarrow 2)\Rightarrow 3)\Rightarrow 1)$ wynikają bezpośrednio z lematu 3.1.

Implikacja $2)\Rightarrow 2a)$ jest oczywista.

Dowód $2a)\Rightarrow 2)$ . Niech $p=\sum _{{i=1}}^{t}\, r_{i}p_{i}$ będzie nietrywialną kombinacją wypukłą punktów z $W$ . To znaczy $\forall _{i}\, r_{i}>0$ i wszystkie punkty są różne. Wtedy $p=r_{1}p_{1}+(1-r_{1})\sum _{{i=2}}^{t}\,\frac{r_{i}}{1-r_{1}}p_{i}$ należy do wnętrza odcinka o końcach $p_{1}$ i $\sum _{{i=2}}^{t}\,\frac{r_{i}}{1-r_{1}}p_{i}$ , a więc jest środkiem pewnego mniejszego odcinka zawartego w $W$ .

∎

Wniosek 3.2

Wielościan ma co najwyżej skończoną liczbę wierzchołków. Dokładniej: Jeżeli $W$ jest wielościanem w $R^{n}$ opisanym przez $t$ półprzestrzeni, to $W$ zawiera co najwyżej $\left(\begin{array}[]{c}t\\ n\end{array}\right)$ wierzchołków.

Algorytm szukania wierzchołków.

Z nierówności opisujących wielościan wybieramy n liniowo

niezależnych. Zamieniamy je na równania i rozwiązujemy otrzymany

układ n równań.

Ponieważ równania są niezależne rozwiązanie jest jednoznaczne.

Jeżeli rozwiązanie spełnia pozostałe nierówności, to otrzymaliśmy

wierzchołek.

Procedurę tą możemy stosować $\left(\begin{array}[]{c}t\\ n\end{array}\right)$ razy.

Analogicznie możemy opisywać krawędzie.

Twierdzenie 3.3

Niech $p$ będzie punktem wielościanu $W\subset R^{n}$ , opisanego układem:

$\left\{\begin{array}[]{c}\alpha _{{1}}\bullet x\,\leq b_{{1}}\\ \alpha _{{2}}\bullet x\,\leq b_{{2}}\\ \cdots\\ \alpha _{{t}}\bullet x\,\leq b_{{t}}\end{array}\right.$ .

Dodatkowo zakładamy, że równania są tak ustawione by:

$\alpha _{{i}}\bullet p\,=b_{{i}}$ dla $1\leq i\leq s$ ;

$\alpha _{{i}}\bullet p\,<b_{{i}}$ dla $s<i\leq t$ ;

Wówczas równoważne są warunki:

1) $p$ jest punktem wewnętrznym krawędzi wielościanu $W$ . $(\, p\in rint(W)\ )$

2) $p$ jest środkiem odcinka zawartego w $W$ , ale nie jest środkiem koła $($ kuli wymiaru 2 $)$ zawartego w $W$ .

3) rząd macierzy $A_{p}=n-1$ gdzie $A_{p}=\left[\begin{array}[]{c}\alpha _{{1}}\\ \alpha _{{2}}\\ ...\\ \alpha _{{s}}\end{array}\right]$ , jest podmacierzą macierzy opisującej $W$ złożoną z pierwszych $s$ wierszy tej macierzy.

Wniosek 3.3

Wielościan ma co najwyżej skończoną liczbę krawędzi. Dokładniej: Jeżeli $W$ jest wielościanem w $R^{n}$ opisanym przez $t$ półprzestrzeni to $W$ zawiera co najwyżej $\left(\begin{array}[]{c}t\\ n-1\end{array}\right)$ krawędzi.

Algorytm szukania krawędzi.

Z nierówności opisujących wielościan wybieramy $n-1$ liniowo

niezależnych. Zamieniamy je na równania i rozwiązujemy otrzymany

układ $n-1$ równań.

Ponieważ równania są niezależne więc rozwiązaniem jest prosta, nazwijmy

ją $l$ . Aby wyliczyć krawędź zawartą w otrzymanej prostej

przedstawiamy ją w postaci parametrycznej $l=q+t\alpha,t\in\mathbb{R}$ .

Wstawiamy równanie prostej

do pozostałych nierówności i

otrzymujemy ograniczenia na $t$ .

Procedurę tą możemy stosować $\left(\begin{array}[]{c}t\\ n-1\end{array}\right)$ razy.

Algorytm szukania krawędzi wychodzących z wierzchołka .

Wypisujemy wszystkie nierówności, które punkt $p$ spełnia jako

równości. Z tego zbioru wybieramy $n-1$ liniowo niezależnych i dalej postępujemy jak w

poprzednim algorytmie.

Twierdzenie 3.4

Niech $\emptyset\neq W\subseteq R^{{n}}$ będzie wielościanem opisanym wzorem W= $\left\{ x\in R^{{n}}\,|\, Ax^{T}\leq b\right\}$ .

Wówczas równoważne są warunki:

1) W zawiera wierzchołek.

2) $rzA=n$ .

3) W nie zawiera prostej.

$1)\Rightarrow 2)$ wniosek z twierdzenia 3.2.

Dowód $2)\Rightarrow 3)$

Przypuśćmy, że $l=\left\{ p+r\alpha\,|\, r\in R\right\}$ jest prostą zawartą w wielościanie $W$ , $(p,\alpha\in R^{{n}})$ . Pokażemy, że prosta $l$ jest zawarta w zbiorze rozwiązań układu równań liniowych o macierzy $[A|b]$ .

$\forall _{{r\in R}}\quad A(p+r\alpha)\leq b$

$A=\overbrace{\left[\begin{array}[]{c}\alpha _{{1}}\\ \alpha _{{2}}\\ ...\\ \alpha _{{t}}\end{array}\right]}^{n}\quad b=\left.\left[\begin{array}[]{c}b_{{1}}\\ b_{{2}}\\ ...\\ b_{{t}}\end{array}\right]\right\} t$

$\forall _{{1\leq i\leq t}}\quad\alpha _{{i}}\bullet(p+r\alpha)\leq b_{{i}}$

$\alpha _{{i}}\bullet p\,+r\alpha _{{i}}\bullet\alpha\leq b_{{i}}$

$r(\alpha _{{i}}\bullet\alpha)\leq b_{{i}}-\alpha _{{i}}\bullet p$

Zatem:

$\forall _{{1\leq i\leq t}}\quad\forall _{{r\in R}}\quad r(\alpha _{{i}}\bullet\alpha)\leq b_{{i}}-\alpha _{{i}}\bullet p\,$ .

Ale $\alpha _{{i}}\bullet\alpha>0\Rightarrow r\leq\frac{b_{{i}}-\alpha _{{i}}\bullet p\,}{\alpha _{{i}}\bullet\alpha}$

$\alpha _{{i}}\bullet\alpha<0\Rightarrow r\geq\frac{b_{{i}}-\alpha _{{i}}\bullet p\,}{\alpha _{{i}}\bullet\alpha}$ .

Co daje $\alpha _{{i}}\bullet\alpha=0$ .

Stąd $\alpha$ jest niezerowym rozwiązaniem jednorodnego układu równań liniowych $A[y]=\theta$ .

Niech $p+r\alpha\in l$ , wtedy $A(p+r\alpha)=rA\alpha+Ap=\theta+b=b$

Skoro wymiar przestrzeni rozwiązań jest $\geq 1$ więc na mocy twierdzenia Kroneckera - Capelli'ego $rzA<n$ .

Sprzeczność.

$3)\Rightarrow 1)$

Niech $S$ będzie ścianą wielościanu $W$ najmniejszego wymiaru. Ponieważ każda ściana $S$ jest ścianą $W$ , więc $S$ nie ma właściwych ścian, a zatem na mocy lematu 3.5 $S$ jest przestrzenią afiniczną. Wielościan $W$ nie zawiera prostej, więc $S$ nie zawiera prostej. Stąd $S$ ma wymiar 0 i jest wierzchołkiem.

∎

Wniosek 3.4

Niech $\emptyset\neq W_{{1}}\subset W_{{2}}$ będą wielościanami. Jeżeli $W_{{2}}$ zawiera wierzchołek to $W_{{1}}$ też zawiera wierzchołek.

$W_{{2}}$ zawiera wierzchołek $\Rightarrow W_{{2}}$ nie zawiera prostej $\Rightarrow W_{{1}}$ nie zawiera prostej $\Rightarrow W_{{1}}$ zawiera wierzchołek.

∎

Wniosek 3.5

Niech $\,\emptyset\neq W=\left\{ x\in R^{{n}}\,|\, Ax=b\ i\ x\geq 0\right\}$ będzie wielościanem.

Wtedy $W$ zawiera wierzchołek.

$W\subset W_{{2}}$ gdzie $W_{{2}}=\left\{ x\in R^{{n}}\,|\, x\geq 0\right\}$ , czyli $\ -x\leq 0$

ale $rz\left[\begin{array}[]{cccc}-1&0&\ldots&0\\ 0&-1&\ldots&0\\ &\vdots&\ldots&\\ 0&0&\ldots&-1\end{array}\right]$ $=n$

Stąd $W_{{2}}$ zawiera wierzchołek, więc $W_{{1}}$ też.

∎

Twierdzenie 3.5

Niech $W\subset\mathbb{R}^{{n}}$ będzie wielościanem z wierzchołkiem. Niech $S$ będzie ścianą wielościanu $W$ . Wówczas $S$ ma wierzchołek i każdy wierzchołek $S$ jest wierzchołkiem $W$ .

$S$ jest wielościanem więc na mocy poprzedniego wniosku zawiera wierzchołek. Przypuśćmy, że $p$ jest wierzchołkiem $S$ . Na mocy wniosku 3.1 $p$ jest ścianą wielościanu $W$ wymiaru 0, a więc wierzchołkiem.

∎

Bezpośrednio stąd wynika.

Wniosek 3.6

Niech $W\subset R^{{n}}$ będzie wielościanem z wierzchołkiem. Wtedy każda krawędź wielościanu $W$ zawiera pewien wierzchołek $W$ .

Zadania

Ćwiczenie 3.1

Niech $W=\bigcap _{{\ i=1}}^{{\ t}}H_{i}\ \subset\mathbb{R}^{n}$ będzie wielościanem. Jeżeli $W\neq\bigcap _{{\ i=2}}^{{\ t}}H_{i}$ to $W\cap\partial H_{1}$ jest ścianą $W$ wymiaru $\geq\ dimW-1$ .

Ćwiczenie 3.2

Niech $S$ będzie skończonym zbiorem punktów przestrzeni $R^{n}$ . Pokazać, że zbiorem wierzchołków $Conv\, S$ jest najmniejszy podzbiór $T\subset S$ , taki że $Conv\, T=Conv\, S$ .

Ćwiczenie 3.3

Pokazać, że jeżeli $W\subset R^{n}$ jest wielościanem wymiaru $k$ , to z każdego wierzchołka wychodzi co najmniej $k$ krawędzi.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Optymalizacja I

Zagadnienia

3. Wierzchołki i krawędzie

3.1. Wierzchołki i krawędzie

Definicja 3.1

Stwierdzenie 3.1

Lemat 3.1

Stwierdzenie 3.2

Lemat 3.2

Lemat 3.3

Lemat 3.4

Lemat 3.5

Twierdzenie 3.1

Wniosek 3.1

Twierdzenie 3.2

Wniosek 3.2

Algorytm szukania wierzchołków.

Twierdzenie 3.3

Wniosek 3.3

Algorytm szukania krawędzi.

Algorytm szukania krawędzi wychodzących z wierzchołka .

Twierdzenie 3.4

Wniosek 3.4

Wniosek 3.5

Twierdzenie 3.5

Wniosek 3.6

Zadania

Ćwiczenie 3.1

Ćwiczenie 3.2

Ćwiczenie 3.3