Zagadnienia
5. Tablice sympleks
5.1. Tablice sympleks
Algorytm sympleks wymaga by obszar dopuszczalny, na którym badamy ekstrema funkcji celu, był wielościanem z wierzchołkiem. Dowolny wielościan możemy ”przerobić” na wielościan z wierzchołkiem przechodząc do zadania równoważnego i zamieniając zmienne tak by były nieujemne.
Jeżeli ![]() to zastępujemy je nową zmienną
to zastępujemy je nową zmienną ![]() , gdzie
, gdzie ![]() .
.
Jeżeli ![]() jest nieograniczone to zastępujemy je różnicą
jest nieograniczone to zastępujemy je różnicą ![]() , gdzie
, gdzie ![]() oraz
oraz ![]() .
.
W szczególności w tym rozdziale będziemy badać wielościany zapisane w postaci kanonicznej czyli ![]() .
.
Opis wierzchołków i krawędzi zadania ![]() w postaci
kanonicznej.
w postaci
kanonicznej.
Niech ![]() będzie
wielościanem. Dodatkowo zakładamy, że równania opisujące
będzie
wielościanem. Dodatkowo zakładamy, że równania opisujące ![]() są
liniowo niezależne -
czyli
są
liniowo niezależne -
czyli ![]() liczba równań.
liczba równań.
Niech ![]() będzie wierzchołkiem
będzie wierzchołkiem ![]() . Ze zbioru równań i ”nierówności
spełnionych jako równości” które spełnia wierzchołek
. Ze zbioru równań i ”nierówności
spełnionych jako równości” które spełnia wierzchołek ![]() wybieramy
wybieramy ![]() liniowo niezależnych w specjalny sposób. Po pierwsze wybieramy
liniowo niezależnych w specjalny sposób. Po pierwsze wybieramy ![]() równań
równań ![]() opisujących wielościan a potem uzupełniamy do
opisujących wielościan a potem uzupełniamy do ![]() liniowo niezależnych równań dodając pewne
liniowo niezależnych równań dodając pewne ![]() .
.
Wynika to z lematu Steinitza o bazie. Dokładniej: ze zbioru równań spełnianych przez ![]() wybieramy dowolnie bazę
wybieramy dowolnie bazę ![]() -
- ![]() liniowo niezależnych równań. Następnie zbiór liniowo niezależny
liniowo niezależnych równań. Następnie zbiór liniowo niezależny ![]() uzupełniamy do bazy równaniami z
uzupełniamy do bazy równaniami z ![]() . Muszą to być równania typu
. Muszą to być równania typu ![]() Otrzymaliśmy układ
Otrzymaliśmy układ ![]() liniowo niezależnych równań z
liniowo niezależnych równań z ![]() niewiadomymi, którego jedynym rozwiązaniem jest punkt
niewiadomymi, którego jedynym rozwiązaniem jest punkt ![]() . Macierz tego układu oznaczmy literą U.
. Macierz tego układu oznaczmy literą U.
Zmienne ![]() nazywamy niebazowymi zaś pozostałe
bazowymi.
nazywamy niebazowymi zaś pozostałe
bazowymi.
Współrzędne niebazowe wierzchołka ![]() są równe
są równe ![]() .
.
Uwaga: Wierzchołek ma co najwyżej ![]() niezerowych współrzędnych.
niezerowych współrzędnych.
Dla ułatwienia przenumerujmy tak zmienne by ![]() były
zmiennymi niebazowymi oraz
były
zmiennymi niebazowymi oraz ![]() zmiennymi bazowymi.
zmiennymi bazowymi.
Wtedy macierz równania opisującego ![]() składa się z 3 części
składa się z 3 części
![]() , gdzie
, gdzie ![]() jest macierzą kwadratową.
jest macierzą kwadratową.
![]() jest odwracalna.
jest odwracalna.
Mnożąc układ równań ![]() z lewej strony przez macierz
z lewej strony przez macierz ![]() otrzymujemy równoważny opis wielościanu
otrzymujemy równoważny opis wielościanu ![]()
![\left[B^{{-1}}N|I\right]x^{T}\,=\, B^{{-1}}b=\left[\begin{array}[]{c}b_{{1}}\\
\vdots\\
b_{{t}}\end{array}\right]](wyklady/op1/mi/mi650.png)
Zaś wierzchołek ma współrzędne
![]() .
.
Podsumowując, każdemu wierzchołkowi, przez wybór zmiennych bazowych przyporządkowujemy układ równań o macierzy zawierającej podmacierz jednostkową.
Definicja 5.1
Tablicą sympleks nazywamy taką macierz rozszerzoną układu
równań ![]() , że
, że ![]() zawiera podmacierz jednostkową rozmiaru t. Dokładniej,
można z macierzy
zawiera podmacierz jednostkową rozmiaru t. Dokładniej,
można z macierzy ![]() tak powykreślać kolumny i poprzestawiać
wiersze by uzyskać macierz jednostkową.
tak powykreślać kolumny i poprzestawiać
wiersze by uzyskać macierz jednostkową.
Tablicę sympleks nazywamy pierwotnie dopuszczalną gdy wszystkie
wyrazy wolne są ![]() . Co zapisujemy
. Co zapisujemy ![]() .
.
Jak pokazaliśmy poprzednio każdemu wierzchołkowi odpowiada co najmniej jedna tablica sympleks pierwotnie dopuszczalna. Dokładniej tyle tablic ile jest możliwości wyboru zmiennych (nie)bazowych.
Stwierdzenie 5.1
Pierwotnie dopuszczalne tablice sympleks opisują wierzchołki.
Niech ![]() będzie tablicą sympleks pierwotnie dopuszczalną. W
macierzy wybieramy kolumny tworzące macierz jednostkową. Zmienne
odpowiadające tym kolumną nazwiemy bazowymi zaś pozostałe
niebazowymi. Zmiennym niebazowym przypisujemy wartość 0. Bazowe
zmienne wyliczamy z układu równań po opuszczeniu zmiennych
niebazowych. Tak więc zmienne bazowe przyjmują wartości wyrazów
wolnych w odpowiedniej kolejności. Otrzymany punkt jest
wierzchołkiem gdyż spełnia
będzie tablicą sympleks pierwotnie dopuszczalną. W
macierzy wybieramy kolumny tworzące macierz jednostkową. Zmienne
odpowiadające tym kolumną nazwiemy bazowymi zaś pozostałe
niebazowymi. Zmiennym niebazowym przypisujemy wartość 0. Bazowe
zmienne wyliczamy z układu równań po opuszczeniu zmiennych
niebazowych. Tak więc zmienne bazowe przyjmują wartości wyrazów
wolnych w odpowiedniej kolejności. Otrzymany punkt jest
wierzchołkiem gdyż spełnia ![]() nierówności jako równania.
nierówności jako równania. ![]() z
równań
z
równań ![]() i
i ![]() z równań
z równań ![]() spełnianych przez zmienne
niebazowe. Dodatkowo równania te są liniowo niezależne.
spełnianych przez zmienne
niebazowe. Dodatkowo równania te są liniowo niezależne.
Twierdzenie 5.1
Niech ![]() będzie
wielościanem. Dodatkowo zakładamy, że równania opisujące
będzie
wielościanem. Dodatkowo zakładamy, że równania opisujące ![]() są
liniowo niezależne -
czyli
są
liniowo niezależne -
czyli ![]() liczba równań. Niech
liczba równań. Niech ![]() będzie wierzchołkiem
będzie wierzchołkiem ![]() . Wówczas:
. Wówczas:
a) Liczba niezerowych współrzędnych wierzchołka ![]() jest nie większa niż liczba równań.
jest nie większa niż liczba równań.
b) Istnieje taka odwracalna podmacierz ![]() macierzy
macierzy ![]() , że
, że ![]() jest tablicą sympleks opisującą wierzchołek
jest tablicą sympleks opisującą wierzchołek ![]() .
.
c) Niech ![]() będzie odwracalną podmacierzą macierzy
będzie odwracalną podmacierzą macierzy ![]() . Wówczas
. Wówczas ![]() jest tablicą sympleks opisującą wierzchołek
jest tablicą sympleks opisującą wierzchołek ![]() wtedy i tylko wtedy gdy macierz
wtedy i tylko wtedy gdy macierz ![]() zawiera wszystkie kolumny
zawiera wszystkie kolumny ![]() , których indeksy są indeksami niezerowych współrzędnych wierzchołka
, których indeksy są indeksami niezerowych współrzędnych wierzchołka ![]() .
.
Stwierdzenie 5.2
Jeżeli w wielościanie ![]() opisanym
opisanym ![]() równaniami wierzchołek
równaniami wierzchołek ![]() ma
ma ![]() niezerowych współrzędnych to jest opisany dokładnie jedną tablicą sympleks.
niezerowych współrzędnych to jest opisany dokładnie jedną tablicą sympleks.
Przykład 5.1
W tablicy sympleks ![\left[\begin{array}[]{ccccccc|c}x_{1}&x_{2}&x_{3}&x_{4}&x_{5}&x_{6}&x_{7}&ww\\
\hline 0&1&5&0&-5&3&0&0\\
1&0&1&1&-2&1&0&1\\
0&0&-6&0&-4&1&1&3\end{array}\right]](wyklady/op1/mi/mi662.png) możemy wybrać kolumny 1, 2 i 7. Niebazowymi
zmiennymi są
możemy wybrać kolumny 1, 2 i 7. Niebazowymi
zmiennymi są ![]() i one przyjmują wartość 0.
Wykreślamy kolumny zmiennych niebazowych i zmienne bazowe
wyliczamy z równania o macierzy
i one przyjmują wartość 0.
Wykreślamy kolumny zmiennych niebazowych i zmienne bazowe
wyliczamy z równania o macierzy ![\left[\begin{array}[]{ccc|c}x_{1}&x_{2}&x_{7}&ww\\
\hline 0&1&0&0\\
1&0&0&1\\
0&0&1&3\end{array}\right]](wyklady/op1/mi/mi707.png) .
Więc
.
Więc ![]() ,
, ![]() i
i ![]() . Wierzchołkiem
jest
. Wierzchołkiem
jest ![]() .
Wybierzmy teraz kolumny 2,
4 i 7. Otrzymamy wierzchołek
.
Wybierzmy teraz kolumny 2,
4 i 7. Otrzymamy wierzchołek ![]() .
.
Algorytm szukania wierzchołków.
| Niech |
| wielościanem. Dodatkowo zakładamy, że równania opisujące |
| liniowo niezależne - czyli |
| Wybieramy maksymalne kwadratowe podmacierze |
| Jeżeli |
| przez |
| Jeżeli otrzymana tablica jest pierwotnie dopuszczalna to opisuje |
| wierzchołek. |
Algorytm opisu krawędzi.
| Niech |
| opisującą wierzchołek |
| wierzchołka. Zaczynamy od wybrania |
| wierzchołek. Nie możemy odrzucać równań z układu |
| pewnej zmiennej niebazowej zamiast |
| Otrzymujemy opis prostej w której zmienna |
| parametrem. Dla ustalenia uwagi przyjmijmy |
![A=[A|b]=\left[\begin{array}[]{ccc|ccccc|c}x_{1}&...&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\
\hline 1&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\
\vdots&\ddots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\
0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]](wyklady/op1/mi/mi589.png) |
| Teraz wyliczamy zmienne bazowe |
| postać |
| Jeżeli wszystkie |
| W przeciwnym |
| przypadku największą wartością |
| dodatnich |
Uwaga 5.1
Liczba ![]() wyznacza długość krawędzi. Jeżeli startujemy z wierzchołka
wyznacza długość krawędzi. Jeżeli startujemy z wierzchołka ![]() i poruszamy się w kierunku
i poruszamy się w kierunku ![]() to
to ![]() jest kolejnym wierzchołkiem. Długością krawędzi jest liczba
jest kolejnym wierzchołkiem. Długością krawędzi jest liczba ![]() .
.
Uwaga 5.2
Jeżeli minimum ![]() to krawędź ma długość 0 ( jest punktem ) i
nazywamy ją krawędzią zdegenerowaną.
to krawędź ma długość 0 ( jest punktem ) i
nazywamy ją krawędzią zdegenerowaną.
Twierdzenie 5.2
Niech ![]() będzie pierwotnie dopuszczalną tablicą sympleks, z ustaloną bazą i opisującą wierzchołek
będzie pierwotnie dopuszczalną tablicą sympleks, z ustaloną bazą i opisującą wierzchołek ![]() . Wówczas
. Wówczas ![]() opisuje
opisuje ![]() krawędzi wychodzących z wierzchołka
krawędzi wychodzących z wierzchołka ![]() i wektory kierunkowe tych krawędzi są liniowo niezależne. Wliczamy krawędzie zdegenerowane zaś
i wektory kierunkowe tych krawędzi są liniowo niezależne. Wliczamy krawędzie zdegenerowane zaś ![]() oznacza liczbę kolumn i
oznacza liczbę kolumn i ![]() liczbę wierszy.
liczbę wierszy.
Ustawmy wektory kierunkowe w macierz a następnie wykreślmy kolumny zmiennych bazowych. Otrzymaliśmy macierz jednostkową ![]() . Zatem wektory były liniowo niezależne.
. Zatem wektory były liniowo niezależne.
Uwaga 5.3
Aby opisać wszystkie krawędzie wychodzące z wierzchołka ![]() należy
użyć wszystkich tablic sympleks opisujących
należy
użyć wszystkich tablic sympleks opisujących ![]() .
.
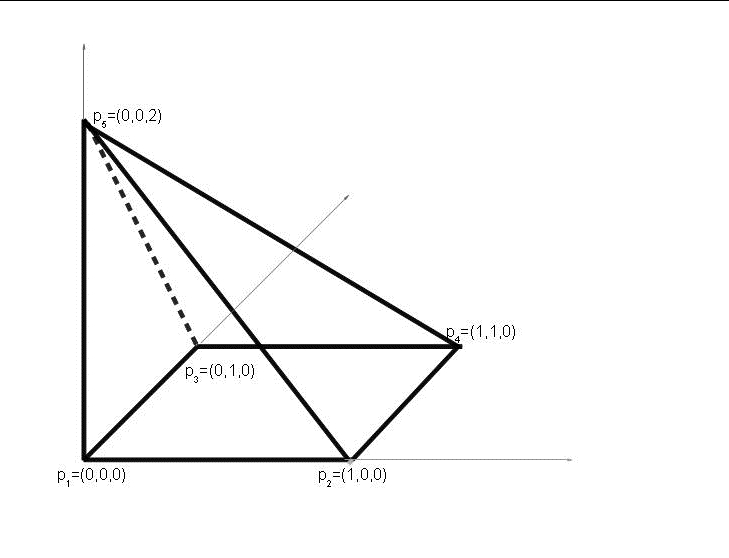
Przykład 5.2
Opiszmy ostrosłup ![]() o podstawie kwadratowej z
wierzchołkami
o podstawie kwadratowej z
wierzchołkami
![]() i o szczycie w punkcie
i o szczycie w punkcie ![]() .
.
![]() jest opisane układem nierówności:
jest opisane układem nierówności:
![]()
![]()
![]()
Przerabiamy nierówności na równania dodając nowe zmienne i otrzymujemy postać kanoniczna:
![]()
![]()
![]()
Zapiszmy w postaci tablicy sympleks:
![TS_{1}=\left[\begin{array}[]{ccccc|c}x_{{1}}&x_{{2}}&x_{{3}}&x_{{4}}&x_{{5}}&ww\\
\hline 2&0&1&1&0&2\\
0&2&1&0&1&2\end{array}\right]](wyklady/op1/mi/mi670.png)
Zmiennymi bazowymi są ![]() i
i ![]() zaś
zaś ![]() opisuje
wierzchołek:
opisuje
wierzchołek:
![]() ,
,
Poruszamy się w kierunku wierzchołka ![]() krawędzią
wyznaczoną przez
krawędzią
wyznaczoną przez ![]() :
:
![TS_{1}=\left[\begin{array}[]{ccccc|c}&&\downarrow&&&\\
x_{{1}}&x_{{2}}&x_{{3}}&x_{{4}}&x_{{5}}&ww\\
\hline 2&0&1&1&0&2\\
0&2&(1)&0&1&2\end{array}\right]](wyklady/op1/mi/mi637.png) .
.
Szukamy elementu centralnego.
![]() zatem możemy
wybrać dowolny element kolumny 3-ciej.
zatem możemy
wybrać dowolny element kolumny 3-ciej.
![TS_{2}=\left[\begin{array}[]{ccccc|c}k_{{1}}&k_{{2}}&&&k_{{3}}&\\
\hline 2&-2&0&1&-1&0\\
0&2&1&0&1&2\end{array}\right]](wyklady/op1/mi/mi613.png) . Zmiennymi bazowymi są teraz
. Zmiennymi bazowymi są teraz
![]() i
i ![]() zaś
zaś ![]() opisuje wierzchołek
opisuje wierzchołek ![]()
Ile krawędzi wychodzi z ![]() ?
?
Z rysunku widać, że 4, zaś tablica ![]() opisuje tylko trzy krawędzie o
wektorach kierunkowych
opisuje tylko trzy krawędzie o
wektorach kierunkowych![]() - krawędź zdegenerowana
(długość 0) gdyż
- krawędź zdegenerowana
(długość 0) gdyż ![]()
![]() w kierunku wierzchołka
w kierunku wierzchołka
![]()
![]() w kierunku wierzchołka
w kierunku wierzchołka
![]()
Wędrując wzdłuż krawędzi zdegenerowanej ![]() znajdujemy nową TS opisującą
znajdujemy nową TS opisującą ![]() .
.
Otrzymujemy ![\left[\begin{array}[]{ccccc|c}k_{{1}}&&&&&\\
\hline(2)&-2&0&1&-1&0\\
0&2&1&0&1&2\end{array}\right]\rightarrow\left[\begin{array}[]{ccccc|c}\hline 1&-1&0&\frac{1}{2}&-\frac{1}{2}&0\\
0&2&1&0&1&2\\
&&B&B&&\end{array}\right]=TS_{3}](wyklady/op1/mi/mi1806.png)
Tablica ![]() opisuje dalej wierzchołek
opisuje dalej wierzchołek ![]() i
krawędzie:
i
krawędzie:
![\left[\begin{array}[]{ccccc|c}&k_{{4}}&&k_{{5}}&k_{{6}}&\\
\hline 1&-1&0&\frac{1}{2}&-\frac{1}{2}&0\\
0&2&1&0&1&2\\
B&&B&&&\end{array}\right]](wyklady/op1/mi/mi1780.png)
![]() w kierunku wierzchołka
w kierunku wierzchołka
![]()
![]() - zdegenerowana
- zdegenerowana ![]()
![]() w kierunku wierzchołka
w kierunku wierzchołka
![]()
Definicja 5.2
Tablicą Sympleks opisującą zadanie programowania liniowego
nazywamy taką macierz, w której pierwszy wiersz reprezentuje
równanie ![]() , pozostałe wiersze równania
, pozostałe wiersze równania
![]() i macierz ta zawiera podmacierz jednostkową. Zwyczajowo
pierwszy wiersz - opisujący funkcję celu jest oddzielony linią
poziomą. Podobnie znak równości przedstawiamy jako linię pionową.
i macierz ta zawiera podmacierz jednostkową. Zwyczajowo
pierwszy wiersz - opisujący funkcję celu jest oddzielony linią
poziomą. Podobnie znak równości przedstawiamy jako linię pionową.
Tablicę sympleks nazywamy dualnie dopuszczalną gdy w wierszu kosztów zredukowanych (nad kreską ) wszystkie
wyrazy są ![]() , dla zadania typu Max lub są
, dla zadania typu Max lub są ![]() , dla zadania typu Min.
, dla zadania typu Min.
Przykład 5.3
Tablicą sympleks dla zadania
Max ![]() , gdy:
, gdy:
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]()
jest
![\left[\begin{array}[]{ccccccc|c}x_{0}&x_{1}&x_{2}&x_{3}&x_{4}&x_{5}&x_{6}&WW\\
1&-2&-6&3&0&0&0&0\\
\hline 0&1&2&-3&1&0&0&3\\
0&2&3&-5&0&1&0&7\\
0&2&-3&-7&0&0&1&8\end{array}\right]](wyklady/op1/mi/mi1785.png)
Funkcję celu zastąpiliśmy równaniem ![]() zaś
podmacierz jednostkowa powstaje z kolumn odpowiadających zmiennym
o indeksach 0,4,5 i 6.
zaś
podmacierz jednostkowa powstaje z kolumn odpowiadających zmiennym
o indeksach 0,4,5 i 6.
Uwaga 5.4
Ponieważ w algorytmie metody sympleks kolumna odpowiadająca zmiennej ![]() nie zmienia się więc zwykle ją pomijamy.
nie zmienia się więc zwykle ją pomijamy.
Zadania
Ćwiczenie 5.1
Poniższe dwie tablice sympleks opisują to samo zadanie PL.
wylicz zmienne od ![]() do
do ![]() .
.
| 1 | 0 | 0 | 2 | -3 | 5 |
| 2 | 1 | 0 | -2 | d | e |
| -3 | a | b | c | 2 | 4 |
| 7 | g | h | 0 | -7 | -3 |
|---|---|---|---|---|---|
| -4 | 1 | 2 | i | 5 | 14 |
| f | 0 | 1 | j | k |
Ćwiczenie 5.2
Wiedząc, że poniższe tablice sympleks dotyczą tego samego zadania programowania liniowego wyznacz nieznane
współczynniki od ![]() do
do ![]() .
.
![\left[\begin{array}[]{ccccc|c}a&b&c&4&-2&-6\\
\hline 3&1&0&d&3&e\\
7&0&1&1&6&f\end{array}\right]](wyklady/op1/mi/mi709.png) oraz
oraz ![\left[\begin{array}[]{ccccc|c}4&g&0&10&0&-2\\
\hline 1&h&0&3&1&2\\
i&-2&1&j&k&3\end{array}\right]](wyklady/op1/mi/mi732.png)
Ćwiczenie 5.3
Wiedząc, że punkt ![]() jest
wierzchołkiem wielościanu
jest
wierzchołkiem wielościanu
![]() , gdzie
, gdzie
![A=\left[\begin{array}[]{cccccc}2&3&-2&1&-1&1\\
2&-1&-5&-3&3&0\\
1&3&0&2&-2&1\end{array}\right]\: b=\left[\begin{array}[]{c}8\\
0\\
7\end{array}\right]](wyklady/op1/mi/mi687.png)
wypisz wszystkie takie macierze ![]() , zawarte w
, zawarte w ![]() , że
, że
![]()
jest tablicą sympleks opisującą ![]() .
.
5.2. Metoda sympleks
Wędrowanie między wierzchołkami, eliminacja Gaussa - Jordana.
W zadaniu PL mamy wierzchołek ![]() opisany tablicą sympleks. Dla
ustalenia uwagi przyjmijmy
opisany tablicą sympleks. Dla
ustalenia uwagi przyjmijmy
![\left[\begin{array}[]{c|ccc|ccccc|c}x_{0}&x_{1}&...&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\
1&0&\ldots&0&-c_{{t+1}}&...&-c_{{i}}&...&-c_{{n}}&b_{0}\\
\hline 0&1&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\
\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\
0&0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]](wyklady/op1/mi/mi683.png)
Zakładamy, że krawędź odpowiadająca zmiennej ![]() jest skończona
i szukamy tablicy sympleks opisującej drugi koniec tej krawędzi.
jest skończona
i szukamy tablicy sympleks opisującej drugi koniec tej krawędzi.
Wyliczamy minimum po wszystkich dodatnich ![]() z liczb
z liczb
![]() czyli liczbę
czyli liczbę
![]() . Wybieramy dowolny współczynnik
. Wybieramy dowolny współczynnik ![]() ,
na którym osiągane jest minimum. Nazywamy go elementem
centralnym. Na następnej tablicy zaznaczony będzie nawiasem.
,
na którym osiągane jest minimum. Nazywamy go elementem
centralnym. Na następnej tablicy zaznaczony będzie nawiasem.
![\left[\begin{array}[]{c|ccccc|ccccc|c}x_{0}&x_{1}&\ldots&x_{j}&\ldots&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\
1&0&\ldots&0&\ldots&0&-c_{{t+1}}&...&-c_{{i}}&...&-c_{{n}}&b_{0}\\
\hline 0&1&\ldots&0&\ldots&0&a_{{1,t+1}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\
\vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\
0&0&\ldots&1&\ldots&0&a_{{j,t+1}}&\ldots&(a_{{j,i}})&\ldots&a_{{j,n}}&b_{j}\\
\vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\
0&0&\ldots&0&\ldots&1&a_{{t,t+1}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]](wyklady/op1/mi/mi626.png)
Teraz j - ty wiersz dzielimy przez ![]() zaś od każdego innego
wiersza
zaś od każdego innego
wiersza ![]() odejmujemy poprawiony j-ty wiersz pomnożony przez
odejmujemy poprawiony j-ty wiersz pomnożony przez
![]() - czyli zerujemy pozostałe miejsca k-tej kolumny.
Otrzymujemy macierz:
- czyli zerujemy pozostałe miejsca k-tej kolumny.
Otrzymujemy macierz:
![\left[\begin{array}[]{c|ccccc|ccccc|c}x_{0}&x_{1}&\ldots&x_{j}&\ldots&x_{t}&x_{{t+1}}&...&x_{i}&...&x_{n}&ww\\
1&0&\ldots&d_{0}&\ldots&0&-c_{{t+1}}^{*}&...&0&...&-c_{{n}}^{*}&b_{0}^{*}\\
\hline 0&1&\ldots&d_{1}&\ldots&0&a_{{1,t+1}}*&...&0&...&a_{{1,n}}^{*}&b_{1}*\\
\vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\
0&0&\ldots&d_{j}&\ldots&0&a_{{j,t+1}}^{*}&\ldots&1&\ldots&a_{{j,n}}^{*}&b_{j}^{*}\\
\vdots&\vdots&\ddots&\vdots&\ddots&\vdots&\vdots&\ddots&\ldots&\ddots&\vdots&\vdots\\
0&0&\ldots&d_{t}&\ldots&1&a_{{t,t+1}}^{*}&\ldots&0&\ldots&a_{{t,n}}^{*}&b_{t}^{*}\end{array}\right]](wyklady/op1/mi/mi729.png) ,
,
gdzie ![]()
Otrzymaliśmy tablicę sympleks. Z bazy wypadła zmienna ![]() a
doszła zmienna
a
doszła zmienna ![]() .
.
Test optymalności i koszty zredukowane. Rozważamy zadanie typu
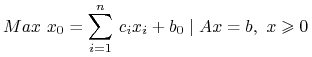 |
opisane tablicą sympleks TS. Oznacza to, że w górnym wierszu TS mamy kolejno liczby
.
Ponieważ jest to tablica sympleks
wszystkie współczynniki ![]() odpowiadające zmiennym bazowym są
równe 0.
odpowiadające zmiennym bazowym są
równe 0.
Jeżeli koszt zredukowany ![]() odpowiadający zmiennej niebazowej
odpowiadający zmiennej niebazowej
![]() jest
jest ![]() (
( ![]() ) to krawędź wyznaczona przez zmienną
) to krawędź wyznaczona przez zmienną
![]() jest poprawiająca. Ponieważ wędrując tą krawędzią zmieniamy
tylko zmienne bazowe nie mające wpływu na funkcję celu i
zwiększamy liczbę
jest poprawiająca. Ponieważ wędrując tą krawędzią zmieniamy
tylko zmienne bazowe nie mające wpływu na funkcję celu i
zwiększamy liczbę ![]() .
.
Jeżeli koszt zredukowany ![]() odpowiadający zmiennej niebazowej
odpowiadający zmiennej niebazowej
![]() jest = 0 (
jest = 0 ( ![]() ) to krawędź wyznaczona przez zmienną
) to krawędź wyznaczona przez zmienną
![]() jest neutralna.
jest neutralna.
Jeżeli koszt zredukowany ![]() odpowiadający zmiennej niebazowej
odpowiadający zmiennej niebazowej
![]() jest
jest ![]() (
( ![]() ) to krawędź wyznaczona przez zmienną
) to krawędź wyznaczona przez zmienną
![]() jest pogarszająca. Ponieważ wędrując tą krawędzią zmieniamy
tylko zmienne bazowe nie mające wpływu na funkcję celu i
zmniejszamy liczbę
jest pogarszająca. Ponieważ wędrując tą krawędzią zmieniamy
tylko zmienne bazowe nie mające wpływu na funkcję celu i
zmniejszamy liczbę
.
Twierdzenie 5.3
Jeżeli w tablicy sympleks opisującej zadanie
![]() wszystkie koszty
zredukowane są
wszystkie koszty
zredukowane są ![]() to tablica ta opisuje wierzchołek
optymalny zadania zaś w prawym górnym rogu tablicy otrzymujemy
optymalną wartość funkcji celu.
to tablica ta opisuje wierzchołek
optymalny zadania zaś w prawym górnym rogu tablicy otrzymujemy
optymalną wartość funkcji celu.
Jeżeli w tablicy sympleks wszystkie koszty zredukowane są ![]() to funkcja celu
to funkcja celu
![]() może być
zapisana tylko przy pomocy zmiennych niebazowych
może być
zapisana tylko przy pomocy zmiennych niebazowych
![]() gdyż dla zmiennych bazowych
gdyż dla zmiennych bazowych ![]() . Funkcja celu
. Funkcja celu ![]() przyjmuje w wierzchołku opisanym tablicą
sympleks wartość
przyjmuje w wierzchołku opisanym tablicą
sympleks wartość ![]() a dla pozostałych punktów wielościanu
a dla pozostałych punktów wielościanu ![]() .
.
Algorytm prosty metody sympleks.
| Rozważamy zadanie typu |
| 0) Start: Dana tablica sympleks pierwotnie dopuszczalna. |
| 1) Test optymalności i wybór kolumny głównej. |
| 1a) Jeżeli wszystkie koszty zredukowane są nieujemne |
| to STOP. Tablica opisuje wierzchołek optymalny. |
| 1b) Jeżeli nie to wybieramy kolumnę |
| zredukowany jest ujemny. |
| 2) Test nieograniczoności i wybór elementu centralnego. |
| 2a) Jeżeli wszystkie elementy kolumny |
| niedodatnie to STOP. Funkcja celu jest nieograniczona. |
| 2b) Jeżeli istnieją |
| że |
| 3) Znajdujemy tablicę sympleks opisującą drugi koniec krawędzi |
| metodą Gaussa - Jordana, GOTO 1). |
Przykład 5.4
Rozwiązujemy zadanie:
Max ![]() , gdy:
, gdy:
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Postacią kanoniczną jest:
Max ![]() , gdy:
, gdy:
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Wierzchołkowi ![]() odpowiada TS
odpowiada TS
![\left[\begin{array}[]{c|cccccc|c}1&-2&-6&3&0&0&0&0\\
\hline 0&(1)&2&-3&1&0&0&3\\
0&2&5&-5&0&1&0&7\\
0&2&-3&-7&0&0&1&8\end{array}\right]](wyklady/op1/mi/mi594.png)
Idziemy krawędzią poprawiająca wyznaczoną przez ![]()
Liczymy ![]() więc jako element centralny wybieramy
więc jako element centralny wybieramy ![]() .
.
Po przekształceniach Gaussa - Jordana Otrzymujemy
![\left[\begin{array}[]{c|cccccc|c}1&0&-2&-3&2&0&0&6\\
\hline 0&1&2&-3&1&0&0&3\\
0&0&1&(1)&-2&1&0&1\\
0&0&-7&-1&-2&0&1&2\end{array}\right]](wyklady/op1/mi/mi588.png)
Tablica ta opisuje wierzchołek ![]()
Idziemy krawędzią poprawiająca wyznaczoną przez ![]()
Liczymy ![]() więc jako
element centralny wybieramy
więc jako
element centralny wybieramy ![]() .
.
Po przekształceniach Gaussa - Jordana Otrzymujemy
![\left[\begin{array}[]{c|cccccc|c}1&0&1&0&-4&3&0&9\\
\hline 0&1&5&0&-5&3&0&6\\
0&0&1&1&-2&1&0&1\\
0&0&-6&0&-4&1&1&3\end{array}\right]](wyklady/op1/mi/mi700.png)
Kolumna odpowiadająca zmiennej ![]() ma ujemny koszt zredukowany
więc na krawędzi przez nią wyznaczonej
ma ujemny koszt zredukowany
więc na krawędzi przez nią wyznaczonej
![]() funkcja celu
funkcja celu ![]() rośnie w nieskończoność.
rośnie w nieskończoność.
5.3. Wymiar zbioru punktów optymalnych.
Twierdzenie 5.4
Niech zadanie ![]() będzie opisane tablicą sympleks pierwotnie i dualnie dopuszczalną. Wówczas zbiór punktów dopuszczalnych zadania ma wymiar nie większy niż liczba zer niebazowych.
będzie opisane tablicą sympleks pierwotnie i dualnie dopuszczalną. Wówczas zbiór punktów dopuszczalnych zadania ma wymiar nie większy niż liczba zer niebazowych.
Przyjmijmy, że tablica sympleks ma ![]() wierszy i
wierszy i ![]() kolumn. Zbiór punktów optymalnych
kolumn. Zbiór punktów optymalnych ![]() jest wielościanem w przestrzeni
jest wielościanem w przestrzeni ![]() opisanym równaniami z tablicy, nierównościami
opisanym równaniami z tablicy, nierównościami ![]() i funkcją celu. Ale jeżeli punkt
i funkcją celu. Ale jeżeli punkt ![]() jest optymalny to jego współrzędne odpowiadające kolumnom poprawiającym muszą być równe zero. Tak więc zbiór punktów optymalnych jest przecięciem stożka opisanego nierównościami
jest optymalny to jego współrzędne odpowiadające kolumnom poprawiającym muszą być równe zero. Tak więc zbiór punktów optymalnych jest przecięciem stożka opisanego nierównościami ![]() i podprzestrzeni
i podprzestrzeni ![]() opisanej równaniami z tablicy i równaniami
opisanej równaniami z tablicy i równaniami ![]() dla
dla ![]() odpowiadających kolumnom poprawiającym. Równania te są liniowo niezależne więc
odpowiadających kolumnom poprawiającym. Równania te są liniowo niezależne więc ![]() . Zatem
. Zatem ![]() .
.
Z twierdzenia 5.4 otrzymujemy bezpośrednio:
Wniosek 5.1
Jeżeli w tablicy sympleks pierwotnie dopuszczalnej wszystkie koszty zredukowane odpowiadające zmiennym niebazowym są ![]() to tablica ta opisuje jedyny wierzchołek
optymalny zadania.
to tablica ta opisuje jedyny wierzchołek
optymalny zadania.
Wniosek 5.2
Jeżeli w tablicy sympleks pierwotnie i dualnie dopuszczalnej każda krawędź neutralna opisywana przez tą tablicę jest niezdegenerowana to wymiar zbioru punktów optymalnych jest równy liczbie tych krawędzi. ( Liczbie zer niebazowych w tablicy sympleks.)
Przyjmijmy, że tablica sympleks opisuje wierzchołek ![]() i wychodzące z niego krawędzie neutralne
i wychodzące z niego krawędzie neutralne ![]() . Wtedy wymiar zbioru punktów optymalnych
. Wtedy wymiar zbioru punktów optymalnych ![]() spełnia warunki:
spełnia warunki: ![]() , gdyż na mocy twierdzenia 5.2 wektory krawędzi są liniowo niezależne. Z drugiej strony
, gdyż na mocy twierdzenia 5.2 wektory krawędzi są liniowo niezależne. Z drugiej strony ![]() na mocy twierdzenia 5.4.
na mocy twierdzenia 5.4.
Wniosek 5.3
Jeżeli tablica sympleks pierwotnie i dualnie dopuszczalna o ![]() wierszach pod kreską ma nad kreską dokładnie
wierszach pod kreską ma nad kreską dokładnie ![]() zer, to:
zer, to:
a) jeżeli krawędź neutralna jest niezdegenerowana to zbiorem punktów optymalnych zadania jest ta krawędź,
b) jeżeli krawędź neutralna jest zdegenerowana to tablica ta opisuje jedyny wierzchołek optymalny zadania.
Ad a) Zbiór punktów optymalnych jest ścianą wielościanu - obszaru dopuszczalnego, zawiera krawędź neutralną opisaną tablicą sympleks i na mocy twierdzenia 5.3 ma wymiar ![]() więc jest tą krawędzią.
więc jest tą krawędzią.
Ad b) Przenumerujmy kolumny tak by tablica sympleks miała postać
![[A|b]=\left[\begin{array}[]{ccc|cccccc|c}0&...&0&0&d_{{t+2}}&...&d_{i}&...&d_{n}&b_{0}\\
\hline 1&\ldots&0&a_{{1,t+1}}&a_{{1,t+2}}&...&a_{{1,i}}&...&a_{{1,n}}&b_{1}\\
\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&a_{{j,i}}&\ddots&\vdots&\vdots\\
0&\ldots&1&a_{{t,t+1}}&a_{{t,t+2}}&\ldots&a_{{t,i}}&\ldots&a_{{t,n}}&b_{t}\end{array}\right]](wyklady/op1/mi/mi1778.png) ,
,
gdzie pierwszych ![]() zmiennych jest bazowych zaś
zmiennych jest bazowych zaś ![]() dla
dla ![]() .
.
Niech ![]() będzie punktem optymalnym. Porównując wartości funkcji celu w punkcie
będzie punktem optymalnym. Porównując wartości funkcji celu w punkcie ![]() opisanym tablicą i w punkcie
opisanym tablicą i w punkcie ![]() otrzymujemy
otrzymujemy ![]() . Więc
. Więc ![]() .
.
Krawędź opisana ![]() -szą kolumną jest zdegenerowana więc istnieje wiersz
-szą kolumną jest zdegenerowana więc istnieje wiersz ![]() taki, że
taki, że ![]() i
i ![]() . Po wstawieniu do
. Po wstawieniu do ![]() -tego równania
-tego równania ![]() otrzymujemy
otrzymujemy ![]() i stąd
i stąd ![]() . W rezultacie punkt
. W rezultacie punkt ![]() spełnia ten sam układ równań co punkt
spełnia ten sam układ równań co punkt ![]() więc
więc ![]() .
.
Przykład 5.5
Jeżeli w tablica sympleks pierwotnie i dualnie dopuszczalna o ![]() wierszach pod kreską ma nad kreską więcej niż
wierszach pod kreską ma nad kreską więcej niż ![]() zer, to wymiar zbioru punktów optymalnych może być każdą liczbą między 0 a liczbą zer niebazowych. Zobaczmy to na przykładzie zadania opisanego tablicą:
zer, to wymiar zbioru punktów optymalnych może być każdą liczbą między 0 a liczbą zer niebazowych. Zobaczmy to na przykładzie zadania opisanego tablicą:
![\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\
\hline 1&0&0&0&0&1&1&1\\
0&1&0&0&0&0&1&2\\
0&0&1&0&\left(1\right)&-2&1&0\\
0&0&0&1&-1&1&1&0\end{array}\right]](wyklady/op1/mi/mi1769.png)
Wierzchołek optymalny ma współrzędne ![]() . Mamy dodatkowo dwie kolumny opisujące zdegenerowane krawędzie neutralne 5-tą i 6-tą. Pokażemy, że zbiór punktów optymalnych jest trójkątem. Po eliminacji Gaussa -
Jordana otrzymujemy inną tablicę opisującą ten sam wierzchołek.
. Mamy dodatkowo dwie kolumny opisujące zdegenerowane krawędzie neutralne 5-tą i 6-tą. Pokażemy, że zbiór punktów optymalnych jest trójkątem. Po eliminacji Gaussa -
Jordana otrzymujemy inną tablicę opisującą ten sam wierzchołek.
![\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\
\hline 1&0&0&0&0&\left(1\right)&1&1\\
0&1&0&0&0&0&1&2\\
0&0&1&0&1&-2&1&0\\
0&0&1&1&0&-1&2&0\end{array}\right]](wyklady/op1/mi/mi1789.png)
Teraz 6-ta kolumna opisuje krawędź niezdegenerowaną. Dochodzimy nią do wierzchołka ![]() opisanego tablicą:
opisanego tablicą:
![\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\
\hline 1&0&0&0&0&1&1&1\\
0&1&0&0&0&0&1&2\\
2&0&1&0&1&0&3&2\\
1&0&\left(1\right)&1&0&0&3&1\end{array}\right]](wyklady/op1/mi/mi1766.png)
Teraz 3-ta kolumna opisuje kolejną krawędź niezdegenerowaną. Dochodzimy nią do wierzchołka ![]() opisanego tablicą:
opisanego tablicą:
![\left[\begin{array}[]{ccccccc|c}0&0&0&0&0&0&3&0\\
\hline(1)&0&0&0&0&1&1&1\\
0&1&0&0&0&0&1&2\\
1&0&0&-1&1&0&0&1\\
1&0&1&1&0&0&3&1\end{array}\right]](wyklady/op1/mi/mi1760.png)
Z tej tablicy możemy dojść do tablicy opisującej wierzchołek ![]() wybierając element centralny w wyznaczonym miejscu.
wybierając element centralny w wyznaczonym miejscu.
Zadania
Ćwiczenie 5.4
Opisz prosty algorytm metody sympleks na przykładzie zadania:
Max ![]() , gdy:
, gdy:
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Ćwiczenie 5.5
Opisz wszystkie punkty optymalne zadania:
![Max\ x_{0}=-4x_{1}+2x_{2}+3x_{3}\\
\begin{array}[]{rl}2x_{1}-x_{2}+x_{3}&\leq 2\\
-6x_{1}+3x_{2}-2x_{3}&\leq 2\\
-7x_{1}+4x_{2}-3x_{3}&\leq 2\end{array}](wyklady/op1/mi/mi634.png)
![]() ,
, ![]() ,
, ![]()