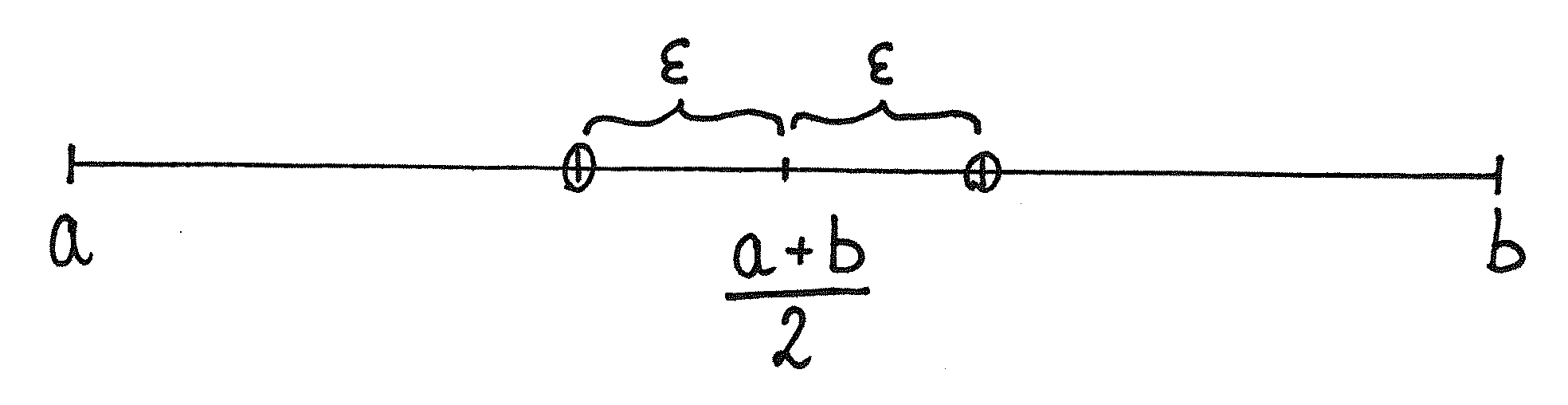12. Metody numeryczne. Optymalizacja bez ograniczeń
W poprzednich rozdziałach budowaliśmy teorię służącą rozwiązywaniu problemów optymalizacyjnych. By być bardziej precyzyjnym, dowiedliśmy twierdzeń, które ułatwiają znalezienie kandydatów na rozwiązania oraz stwierdzenie, czy któryś z nich jest rozwiązaniem. Niestety w obu tych krokach musimy rozwiązywać układy równań nieliniowych. W praktycznych zadaniach optymalizacyjnych układy te mogą nie mieć ”ładnych” rozwiązań lub po prostu nie jesteśmy w stanie ich znaleźć w sposób analityczny. Pozostaje wówczas zastosowanie metod numerycznych, które pozwolą na przybliżenie rozwiązania. W tym i kolejnych rozdziałach opiszemy kilka takich algorytmów numerycznych. Algorytmy te będą raczej atakowały problem optymalizacyjny bezpośrednio (tzn. nie będziemy się starali znaleźć zbioru punktów spełniających warunek konieczny pierwszego rzędu). Będą one krok po kroku tworzyły ciąg punktów zbiegający do rozwiązania. Nie oznacza to jednak, że mnożniki Lagrange'a i metody dualne są nieprzydatne przy tworzeniu algorytmów numerycznych. Wręcz przeciwnie. W przypadku ograniczeń równościowych klasyczne podejście wiedzie właśnie poprzez mnożniki Lagrange'a (tzw. metoda mnożników Lagrange'a), patrz monografie Bazaraa, Sherali, Shetty [3] oraz Bertsekas [4, 5]. My jednak pójdziemy inną drogą, gdyż możemy poświęcić optymalizacji z ograniczeniami zaledwie jeden rozdział.
Na kolejnych stronach będziemy opisywać algorytmy optymalizacyjne oraz analizować ich działanie. Ta analiza powinna zawierać następujące punkty:
zbieżność do rozwiązania (poprawność algorytmu),
warunek końca (kiedy możemy przerwać wykonywanie programu, ponieważ znaleziony punkt jest dostatecznie blisko rozwiązania),
szybkość zbieżności do rozwiązania.
W tym rozdziale opiszemy metody optymalizacyjne na prostej. Będą one konieczne do zaimplementowania algorytmów optymalizacyjnych w wyższym wymiarze, którymi zajmiemy się w roz. 13. Zadania z ograniczeniami rozważymy w roz. 14.
12.1. Optymalizacja bez użycia pochodnych
Zanim przejdziemy do dyskusji właściwego algorytmu, wprowadzimy pojęcie funkcji ściśle quasi-wypukłej i jej własności.
Definicja 12.1
Niech ![]() będzie zbiorem wypukłym. Funkcję
będzie zbiorem wypukłym. Funkcję ![]() nazywamy ściśle quasi-wypukłą, jeśli dla dowolnych
nazywamy ściśle quasi-wypukłą, jeśli dla dowolnych ![]() ,
, ![]() oraz
oraz ![]() zachodzi
zachodzi
Dowód poniższych własności funkcji quasi-wypukłych pozostawiamy jako ćwiczenie.
Lemat 12.1
Funkcja quasi-wypukła ma co najwyżej jedno minimum (lokalne i globalne).
Funkcja ściśle wypukła jest ściśle quasi-wypukła.
Funkcja określona na prostej lub otwartym przedziale jest ściśle quasi-wypukła jeśli jest ściśle malejąca, ściśle rosnąca lub istnieje punkt
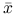 w jej dziedzinie o tej własności, że funkcja jest ściśle malejąca dla
w jej dziedzinie o tej własności, że funkcja jest ściśle malejąca dla 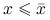 i ściśle rosnąca dla
i ściśle rosnąca dla 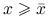 .
.
Okazuje się, że własność ścisłej quasi-wypukłości pozwala na skonstruowanie algorytmu znajdowania minimum funkcji na domkniętym odcinku bez wykorzystania pochodnych. Główna obserwacja znajduje się w poniższym lemacie:
Lemat 12.2
Niech ![]() będzie funkcją ściśle quasi-wypukłą i
będzie funkcją ściśle quasi-wypukłą i ![]() .
.
Jeśli
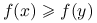 , to
, to 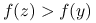 dla każdego
dla każdego 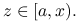
Jeśli
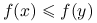 , to
, to 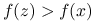 dla każdego
dla każdego ![z\in(y,b].](wyklady/op2/mi/mi1846.png)
Dowód
Udowodnimy punkt (1) przez sprzeczność. Przypuśćmy, że istnieje ![]() o tej własności, że
o tej własności, że ![]() . Wówczas z quasi-wypukłości
. Wówczas z quasi-wypukłości ![]() wynika, że
wynika, że ![]() , co przeczy założeniu, że
, co przeczy założeniu, że ![]() Dowód punktu (2) jest analogiczny.
Dowód punktu (2) jest analogiczny.
Idea algorytmu jest bardzo prosta. Szukając minimum funkcji ściśle quasi-wypukłej ![]() wybieramy mały
wybieramy mały ![]() i porównujemy wartości w punktach
i porównujemy wartości w punktach ![]() i
i ![]() (patrz rys. 12.1). Jeśli
(patrz rys. 12.1). Jeśli ![]() , to minimum znajduje się w przedziale
, to minimum znajduje się w przedziale ![]() . W przeciwnym przypadku jest ono w przedziale
. W przeciwnym przypadku jest ono w przedziale ![]()
Algorytm wygląda następująco:
Inicjalizacja: Wybierz
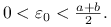 Połóż
Połóż 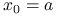 ,
, 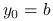 .
.Krok
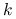 -ty:
-ty:Jeśli
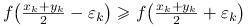 , to
, to 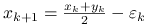 i
i 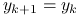 .
.W przeciwnym przypadku
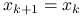 oraz
oraz 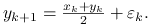
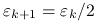 .
.
Koniec: gdy różnica
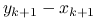 jest dostatecznie mała.
jest dostatecznie mała.
Załóżmy, że istnieje minimum ![]() funkcji
funkcji ![]() na przedziale
na przedziale ![]() (tak być nie musi, patrz zadanie 12.2). Na mocy lematu 12.2 minimum to leży w przedziale
(tak być nie musi, patrz zadanie 12.2). Na mocy lematu 12.2 minimum to leży w przedziale ![]() dla każdego
dla każdego ![]() Długość tego przedziału dąży do zera, co pociąga zbieżność zarówno
Długość tego przedziału dąży do zera, co pociąga zbieżność zarówno ![]() jak i
jak i ![]() do rozwiązania
do rozwiązania ![]() Dowiedliśmy zatem poprawności algorytmu.
Dowiedliśmy zatem poprawności algorytmu.
Jeśli zatrzymamy się w kroku ![]() -tym, to dokładność wyznaczenia punktu minimum zadana jest przez długość przedziału
-tym, to dokładność wyznaczenia punktu minimum zadana jest przez długość przedziału ![]() . Uzasadnia to wybór warunku końca. Niestety, ze względu na brak założeń dotyczących różniczkowalności, nie możemy nic powiedzieć, jak dokładnie przybliżamy wartość funkcji w punkcie minimum.
. Uzasadnia to wybór warunku końca. Niestety, ze względu na brak założeń dotyczących różniczkowalności, nie możemy nic powiedzieć, jak dokładnie przybliżamy wartość funkcji w punkcie minimum.
W zadaniu 12.3 pokażemy, że długość przedziału ![]() zmniejsza się wykładniczo szybko, tzn. istnieje stała
zmniejsza się wykładniczo szybko, tzn. istnieje stała ![]() , taka że
, taka że
Pamiętając, że rozwiązanie ![]() leży w tym przedziale dla każdego
leży w tym przedziale dla każdego ![]() , wnioskujemy, iż zbieżność
, wnioskujemy, iż zbieżność ![]() i
i ![]() do rozwiązania
do rozwiązania ![]() jest wykładnicza.
jest wykładnicza.
12.2. Metoda Newtona
Metoda Newtona służy do znajdowania zer funkcji różniczkowalnej. Stosując ją do funkcji ![]() możemy znaleźć miejsce zerowania się pochodnej funkcji
możemy znaleźć miejsce zerowania się pochodnej funkcji ![]() lub inaczej punkt krytyczny. Jeśli
lub inaczej punkt krytyczny. Jeśli ![]() jest pseudowypukła, to punkt krytyczny pokrywa się z minimum funkcji. W pozostałych przypadkach, znaleziony punkt może być tylko punktem przegięcia funkcji.
jest pseudowypukła, to punkt krytyczny pokrywa się z minimum funkcji. W pozostałych przypadkach, znaleziony punkt może być tylko punktem przegięcia funkcji.
Dla przypomnienia wyprowadzimy metodę Newtona dla znajdowania minimum funkcji. Załóżmy, że funkcja ![]() jest dwukrotnie różniczkowalna. Przybliżamy ją wokół punktu
jest dwukrotnie różniczkowalna. Przybliżamy ją wokół punktu ![]() za pomocą wielomianu Taylora drugiego stopnia:
za pomocą wielomianu Taylora drugiego stopnia:
Zamiast minimalizować funkcję ![]() szukamy minimum jej przybliżenia. Aby miało to sens musimy założyć, że
szukamy minimum jej przybliżenia. Aby miało to sens musimy założyć, że ![]() . Różniczkując prawą stronę po
. Różniczkując prawą stronę po ![]() dostajemy wzór na punkt krytyczny przybliżenia Taylora:
dostajemy wzór na punkt krytyczny przybliżenia Taylora:
Zauważmy, że jeśli w punkcie ![]() zeruje się pochodna
zeruje się pochodna ![]() , to
, to ![]() . To daje nadzieję na poprawność podejścia. Dokładniejsze wyniki podamy po zapisaniu algorytmu:
. To daje nadzieję na poprawność podejścia. Dokładniejsze wyniki podamy po zapisaniu algorytmu:
Inicjalizacja: Wybierz punkt początkowy
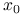 i dokładność
i dokładność 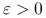 .
.Krok
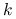 -ty:
-ty: 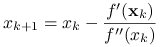
Koniec: gdy
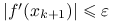 .
.
Powyższy algorytm niesie ze sobą wiele wątpliwości. Po pierwsze, nie jest wcale jasne, czy ciąg ![]() ma granicę. Co więcej, łatwo znaleźć niezdegenerowany przykład, żeby był on rozbieżny (patrz zadanie 12.4). Rozumiemy przez to, że funkcja przyjmuje minimum globalne w pewnym punkcie, lecz nieodpowiedni wybór punktu początkowego
ma granicę. Co więcej, łatwo znaleźć niezdegenerowany przykład, żeby był on rozbieżny (patrz zadanie 12.4). Rozumiemy przez to, że funkcja przyjmuje minimum globalne w pewnym punkcie, lecz nieodpowiedni wybór punktu początkowego ![]() może spowodować, że ciąg
może spowodować, że ciąg ![]() zbiega do nieskończoności. W poniższym lemacie pokazujemy warunek dostateczny, aby taki przypadek nie miał miejsca. Co więcej, w lemacie tym podajemy warunki dostateczne tego, by zbieżność do minimum lokalnego była wykładniczo szybka.
zbiega do nieskończoności. W poniższym lemacie pokazujemy warunek dostateczny, aby taki przypadek nie miał miejsca. Co więcej, w lemacie tym podajemy warunki dostateczne tego, by zbieżność do minimum lokalnego była wykładniczo szybka.
Lemat 12.3
Załóżmy, że ![]() jest funkcją klasy
jest funkcją klasy ![]() na otoczeniu minimum lokalnego
na otoczeniu minimum lokalnego ![]() oraz
oraz ![]() . Wówczas istnieje
. Wówczas istnieje ![]() , taka że dla
, taka że dla ![]() mamy
mamy
Dowód
Z ciągłości ![]() na otoczeniu
na otoczeniu ![]() oraz z tego, że
oraz z tego, że ![]() wynika istnienie
wynika istnienie ![]() o następującej własności:
o następującej własności:
| (12.1) |
Załóżmy, że ![]() . Z definicji
. Z definicji ![]() dostajemy
dostajemy
gdzie w ostatniej równości skorzystaliśmy z równości ![]() . Sprowadzamy prawą stronę do wspólnego mianownika i stosujemy twierdzenie o wartości średniej do różnicy pochodnych:
. Sprowadzamy prawą stronę do wspólnego mianownika i stosujemy twierdzenie o wartości średniej do różnicy pochodnych:
gdzie ![]() należy do przedziału o końcach w
należy do przedziału o końcach w ![]() i
i ![]() . Obkładamy obie strony wartością bezwzględną i stosujemy oszacowanie (12.1) dla
. Obkładamy obie strony wartością bezwzględną i stosujemy oszacowanie (12.1) dla ![]() i
i ![]() .
.
Wniosek 12.1
Przy założeniach powyższego lematu, jeśli ![]() to
to ![]() dla wszystkich
dla wszystkich ![]() .
.
Drugą bolączką metody Newtona jest to, iż zbiega ona do punktu krytycznego, który może również wyznaczać maksimum lokalne lub punkt przegięcia. Założenie pseudowypukłości funkcji ![]() gwarantuje, że punkt krytyczny jest minimum. W pozostałych przypadkach należy zbadać zachowanie funkcji w otoczeniu znalezionego numerycznie punktu krytycznego i na tej podstawie ustalić, czy jest w nim minimum, maksimum lub punkt przegięcia.
gwarantuje, że punkt krytyczny jest minimum. W pozostałych przypadkach należy zbadać zachowanie funkcji w otoczeniu znalezionego numerycznie punktu krytycznego i na tej podstawie ustalić, czy jest w nim minimum, maksimum lub punkt przegięcia.
Pozostaje jeszcze pytanie o warunek końca. Poniższy lemat podaje jego uzasadnienie.
Lemat 12.4
Niech ![]() będzie minimum lokalnym funkcji
będzie minimum lokalnym funkcji ![]() . Załóżmy, że na przedziale
. Załóżmy, że na przedziale ![]() zawierającym
zawierającym ![]() w swoim wnętrzu funkcja
w swoim wnętrzu funkcja ![]() jest dwukrotnie różniczkowalna (niekoniecznie klasy
jest dwukrotnie różniczkowalna (niekoniecznie klasy ![]() ) oraz
) oraz
Wówczas dla każdego ![]() mamy
mamy
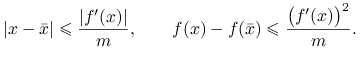 |
Dowód
Ustalmy ![]() . Stosujemy tw. Taylora, tw. 1.10, dwukrotnie (przypomnijmy, że
. Stosujemy tw. Taylora, tw. 1.10, dwukrotnie (przypomnijmy, że ![]() ):
):
gdzie ![]() leżą w przedziale o końcach
leżą w przedziale o końcach ![]() i
i ![]() , a więc również w przedziale
, a więc również w przedziale ![]() . Podstawiamy pierwsze równanie do drugiego:
. Podstawiamy pierwsze równanie do drugiego:
Obkładamy obydwie strony modułem i dzielimy przez ![]() dostając
dostając
Przypomnijmy, że druga pochodna ![]() jest ograniczona z dołu przez
jest ograniczona z dołu przez ![]() na
na ![]() . Zatem
. Zatem ![]() , skąd pierwsza część tezy wynika natychmiastowo.
, skąd pierwsza część tezy wynika natychmiastowo.
Drugą nierówność lematu uzyskujemy znów ze wzoru Taylora:
gdzie ostatnia nierówność wynika z tego, że ![]() . Dowód kończymy mnożąc obie strony nierówności przez
. Dowód kończymy mnożąc obie strony nierówności przez ![]() , obkładając modułem i wstawiając uzyskane wcześniej oszacowanie na
, obkładając modułem i wstawiając uzyskane wcześniej oszacowanie na ![]() .
.
Zwróćmy uwagę, że wszystkie matematyczne wyniki dla metody Newtona zakładają dodatniość drugiej pochodnej, a zatem ścisłą wypukłość. W pozostałych przypadkach ocena wyników i dobór parametrów ![]() pozostaje powierzyć intuicji i doświadczeniom. Nie przeszkadza to wszakże w powszechnym stosowaniu metody Newtona i jej różnych modyfikacji. Zainteresowany czytelnik znajdzie dużo więcej informacji w monografii D. Bertsekas'a [4].
pozostaje powierzyć intuicji i doświadczeniom. Nie przeszkadza to wszakże w powszechnym stosowaniu metody Newtona i jej różnych modyfikacji. Zainteresowany czytelnik znajdzie dużo więcej informacji w monografii D. Bertsekas'a [4].
12.3. Zadania
Ćwiczenie 12.1
Udowodnij lemat 12.1
Ćwiczenie 12.2
Znajdź przykład funkcji ściśle quasi-wypukłej określonej na przedziale domkniętym, która nie przyjmuje swojego infimum, czyli zadanie minimalizacyjne nie ma rozwiązania.
Ćwiczenie 12.3
Wykaż, że w metodzie optymalizacji bez użycia pochodnych długość przedziału ![]() zmniejsza się w sposób wykładniczy, tzn. istnieje stała
zmniejsza się w sposób wykładniczy, tzn. istnieje stała ![]() , taka że
, taka że
Ćwiczenie 12.4
Podaj przykład funkcji ![]() oraz punktu startowego
oraz punktu startowego ![]() , takich żeby ciąg generowany przez metodę Newtona nie miał granicy. Dodatkowo wymagamy, aby funkcja
, takich żeby ciąg generowany przez metodę Newtona nie miał granicy. Dodatkowo wymagamy, aby funkcja ![]() miała minimum globalne w
miała minimum globalne w ![]() .
.
Rozważ funkcję malejącą przy ![]() dążącym do nieskończoności.
dążącym do nieskończoności.
Przeprowadź dowód bez użycia oszacowania na ![]() . Skorzystaj oczywiście z twierdzenia Taylora.
. Skorzystaj oczywiście z twierdzenia Taylora.
Ćwiczenie 12.6
Opracuj szybki algorytm minimalizowania funkcji wypukłej ![]() klasy
klasy ![]() .
.