13. Metody spadkowe
W tym rozdziale przyjrzymy się wielowymiarowym metodom optymalizacji bez ograniczeń. Zakładamy, że ![]() jest funkcją klasy
jest funkcją klasy ![]() . Naszym celem jest znalezienie jej minimum. Wszystkie opisywane metody zbudowane są w oparciu o następujący ogólny schemat. Startujemy z punktu początkowego
. Naszym celem jest znalezienie jej minimum. Wszystkie opisywane metody zbudowane są w oparciu o następujący ogólny schemat. Startujemy z punktu początkowego ![]() , który w naszym przekonaniu znajduje się blisko minimum. W kolejnych krokach generujemy
, który w naszym przekonaniu znajduje się blisko minimum. W kolejnych krokach generujemy ![]() w ten sposób, aby
w ten sposób, aby ![]() . Spodziewamy się, że w ten sposób dojdziemy aż do minimum
. Spodziewamy się, że w ten sposób dojdziemy aż do minimum ![]() . Może się jednak okazać, że punkty skupienia ciągu
. Może się jednak okazać, że punkty skupienia ciągu ![]() nie będą rozwiązaniami. Na kolejnych stronach tego rozdziału zajmiemy się opisem różnych metod konstrukcji ciągu
nie będą rozwiązaniami. Na kolejnych stronach tego rozdziału zajmiemy się opisem różnych metod konstrukcji ciągu ![]() i ich zbieżnością do rozwiązania. Wszystkie wyniki tego rozdziału w oczywisty sposób przenoszą się na przypadek funkcji określonych na zbiorach otwartych w
i ich zbieżnością do rozwiązania. Wszystkie wyniki tego rozdziału w oczywisty sposób przenoszą się na przypadek funkcji określonych na zbiorach otwartych w ![]() .
.
Sformułujmy ściśle problem optymalizacyjny:
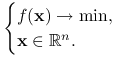 |
Metodami spadkowymi nazywamy takie algorytmy, w których kolejny punkt ![]() zadany jest wzorem
zadany jest wzorem
gdzie ![]() oraz
oraz ![]() jest kierunkiem spadku, tzn.
jest kierunkiem spadku, tzn.
Zauważmy, że dla dostatecznie małych ![]() mamy
mamy ![]() (patrz zadanie 13.1). Możemy więc liczyć, że przy dobrym doborze
(patrz zadanie 13.1). Możemy więc liczyć, że przy dobrym doborze ![]() ciąg punktów
ciąg punktów ![]() będzie zbiegał do minimum. Niestety nie możemy zagwarantować, że będzie to minimum globalne, ale będziemy starać się znaleźć sposób na zapewnienie zbieżności do minimum lokalnego.
będzie zbiegał do minimum. Niestety nie możemy zagwarantować, że będzie to minimum globalne, ale będziemy starać się znaleźć sposób na zapewnienie zbieżności do minimum lokalnego.
W tym rozdziale skupimy się na metodach największego spadku, czyli takich że ![]() jest równoległe do
jest równoległe do ![]() . Metody spadkowe będą również grały pierwsze skrzypce w następnym rozdziale, przy optymalizacji numerycznej z ograniczeniami.
. Metody spadkowe będą również grały pierwsze skrzypce w następnym rozdziale, przy optymalizacji numerycznej z ograniczeniami.
Algorytm opisujący metody największego spadku jest dość prosty:
Inicjalizacja: Wybierz punkt początkowy
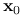 .
.Krok
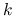 -ty:
-ty:Wybierz krok
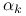 .
.Połóż
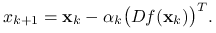
Koniec: gdy
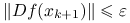 .
.
Pozostaje doprecyzowanie reguł znajdowania kroku ![]() . Reguły te są stosowane dla dowolnych kierunków spadku
. Reguły te są stosowane dla dowolnych kierunków spadku ![]() i w takiej formie je prezentujemy. Czytelnik powinien pamiętać, że w przypadku metod największego spadku
i w takiej formie je prezentujemy. Czytelnik powinien pamiętać, że w przypadku metod największego spadku ![]() .
.
reguła minimalizacji: wybierz
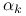 takie że
takie że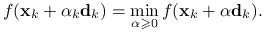
reguła ograniczonej minimalizacji: ustalmy
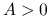 . Wybierz
. Wybierz 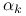 takie że
takie że![f(\mathbf{x}_{k}+\alpha _{k}\mathbf{d}_{k})=\min _{{\alpha\in[0,A]}}f(\mathbf{x}_{k}+\alpha\mathbf{d}_{k}).](wyklady/op2/mi/mi1990.png)
reguła Armijo: ustalmy
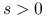 i
i 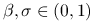 . Połóżmy
. Połóżmy 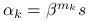 , gdzie
, gdzie 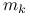 jest najmniejszą liczbą całkowitą nieujemną
jest najmniejszą liczbą całkowitą nieujemną 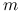 spełniającą nierówność
spełniającą nierówność
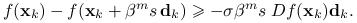
Więcej szczegółów podajemy w poniższych podrozdziałach.
13.1. Reguły minimalizacyjne
Reguła minimalizacji jest dobrze określona, jeśli minimum po prawej stronie istnieje. Do jej implementacji możemy zastosować wówczas metodę Newtona opisaną w poprzednim rozdziale. Ograniczenie przedziału poszukiwań kroku ![]() do
do ![]() ma dwie zalety. Po pierwsze zadanie to ma zawsze rozwiązanie, gdyż minimalizujemy funkcję ciągłą na zbiorze zwartym. Po drugie, możemy zastosować szybsze metody poszukiwania minimum podobne do optymalizacji bez użycia pochodnych opisanej w poprzednim rozdziale.
ma dwie zalety. Po pierwsze zadanie to ma zawsze rozwiązanie, gdyż minimalizujemy funkcję ciągłą na zbiorze zwartym. Po drugie, możemy zastosować szybsze metody poszukiwania minimum podobne do optymalizacji bez użycia pochodnych opisanej w poprzednim rozdziale.
W zadaniu 13.1 dowodzimy, że obie reguły minimalizacyjne wyznaczają krok o tej własności, że ![]() Pozostają jednak dwa pytania: czy warunek końca jest poprawny i czy ciąg
Pozostają jednak dwa pytania: czy warunek końca jest poprawny i czy ciąg ![]() zbiega do minimum.
zbiega do minimum.
W poniższym twierdzeniu dowodzimy, że każdy punkt skupienia ciągu ![]() jest punktem krytycznym, tzn. zeruje się w nim pochodna. Nie jest jednak w ogólności prawdą, że musi w nim być minimum lokalne. Dopiero założenie, że funkcja
jest punktem krytycznym, tzn. zeruje się w nim pochodna. Nie jest jednak w ogólności prawdą, że musi w nim być minimum lokalne. Dopiero założenie, że funkcja ![]() jest pseudowypukła daje nam pewność, że w znalezionym punkcie jest minimum, które dodatkowo jest globalne.
jest pseudowypukła daje nam pewność, że w znalezionym punkcie jest minimum, które dodatkowo jest globalne.
Twierdzenie 13.1
Niech ![]() będzie ciągiem skonstruowanym przy pomocy metody największego spadku z regułą minimalizacji lub minimalizacji ograniczonej. Wówczas każdy punkt skupienia tego ciągu jest punktem krytycznym.
będzie ciągiem skonstruowanym przy pomocy metody największego spadku z regułą minimalizacji lub minimalizacji ograniczonej. Wówczas każdy punkt skupienia tego ciągu jest punktem krytycznym.
Dowód
Dowód przeprowadzimy przez sprzeczność. Niech ![]() będzie punktem skupienia, zaś
będzie punktem skupienia, zaś ![]() podciągiem do niego zbieżnym. Załóżmy, że
podciągiem do niego zbieżnym. Załóżmy, że ![]() Głównym pomysłem dowodu będzie pokazanie, że istnieje stała
Głównym pomysłem dowodu będzie pokazanie, że istnieje stała ![]() , taka że dla dostatecznie dużych
, taka że dla dostatecznie dużych ![]() , tzn. dla
, tzn. dla ![]() dostatecznie bliskich
dostatecznie bliskich ![]() , zachodzi
, zachodzi
czyli możliwe jest zmniejszenie wartości funkcji ![]() w kroku
w kroku ![]() o co najmniej
o co najmniej ![]() Pamiętając, że funkcja
Pamiętając, że funkcja ![]() maleje wzdłuż ciągu
maleje wzdłuż ciągu ![]() mamy
mamy
Przechodząc do granicy z ![]() i korzystając z ciągłości
i korzystając z ciągłości ![]() dostajemy sprzeczność z dodatniością
dostajemy sprzeczność z dodatniością ![]() .
.
Do zakończenia dowodu pozostaje nam udowodnienie istnienia takiej stałej ![]() . Na mocy ciągłości pochodnej (przypomnijmy, że w tym rozdziale zakładamy, że
. Na mocy ciągłości pochodnej (przypomnijmy, że w tym rozdziale zakładamy, że ![]() jest klasy
jest klasy ![]() ) istnieje otoczenie
) istnieje otoczenie ![]() punktu
punktu ![]() , takie że
, takie że
| (13.1) |
Głównym spostrzeżeniem pozwalającym na uzasadnienie powyższej nierówności jest to, że na pewnym otoczeniu ![]() norma pochodnej
norma pochodnej ![]() jest ściśle oddzielona od zera.
jest ściśle oddzielona od zera.
Weźmy ![]() , takie że
, takie że ![]() oraz dodatkowo w przypadku reguły minimalizacji ograniczonej
oraz dodatkowo w przypadku reguły minimalizacji ograniczonej ![]() (zauważmy, że
(zauważmy, że ![]() na mocy (13.1)). Dla
na mocy (13.1)). Dla ![]() punkt
punkt ![]() należy do
należy do ![]() , a więc również do
, a więc również do ![]() . Z twierdzenia o wartości średniej dostajemy
. Z twierdzenia o wartości średniej dostajemy
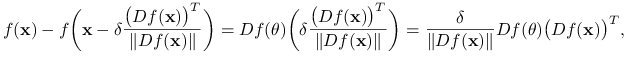 |
gdzie ![]() jest punktem pośrednim, a więc należy do
jest punktem pośrednim, a więc należy do ![]() . Zajmijmy się teraz produktem pochodnych:
. Zajmijmy się teraz produktem pochodnych:
Wstawiamy to oszacowanie do poprzedniego wzoru:
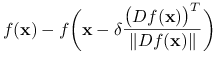 |
|||
gdzie ostatnia nierówność wynika z (13.1). Powyższe oszacowanie jest prawdziwe dla dowolnego ![]() a więc dla
a więc dla ![]() dla dostatecznie dużych
dla dostatecznie dużych ![]() . Możemy zatem przyjąć
. Możemy zatem przyjąć
Powyższe twierdzenie dowodzi poprawności metody największego spadku, lecz nie mówi nic o szybkości zbieżności i o warunku końca. Wzmacniając założenia będziemy mogli dowieść, że zbieżność jest wykładniczo szybka oraz, podobnie jak w lemacie 12.4, warunek końca jest poprawny.
Zdefiniujmy zbiór ![]() , gdzie
, gdzie ![]() jest punktem początkowym.
Oznaczmy przez
jest punktem początkowym.
Oznaczmy przez ![]() najmniejszą wartość własną macierzy drugich pochodnych
najmniejszą wartość własną macierzy drugich pochodnych ![]() , zaś przez
, zaś przez ![]() – jej największą wartość własną.
– jej największą wartość własną.
Lemat 13.1
Załóżmy, że zbiór ![]() jest wypukły, funkcja
jest wypukły, funkcja ![]() jest klasy
jest klasy ![]() na otoczeniu
na otoczeniu ![]() oraz
oraz ![]() . Wówczas punkt minimum
. Wówczas punkt minimum ![]() należy do
należy do ![]() oraz dla dowolnego
oraz dla dowolnego ![]()
Dowód lematu 13.1 pozostawiamy jako ćwiczenie. Zauważmy, że założenie o wypukłości ![]() jest dość naturalne. Jeśli macierz
jest dość naturalne. Jeśli macierz ![]() jest dodatnio określona, to na pewnej kuli
jest dodatnio określona, to na pewnej kuli ![]() o środku w
o środku w ![]() funkcja
funkcja ![]() jest wypukła. Jeśli
jest wypukła. Jeśli ![]() jest jedynym minimum globalnym, to biorąc
jest jedynym minimum globalnym, to biorąc ![]() dostatecznie bliskie
dostatecznie bliskie ![]() dostajemy, że zbiór poziomicowy
dostajemy, że zbiór poziomicowy ![]() jest zawarty w kuli
jest zawarty w kuli ![]() i wnioskujemy dalej, że jest on wypukły.
i wnioskujemy dalej, że jest on wypukły.
Lemat 13.2
Załóżmy, że zbiór ![]() jest wypukły, funkcja
jest wypukły, funkcja ![]() jest klasy
jest klasy ![]() na otoczeniu
na otoczeniu ![]() oraz
oraz ![]() . Oznaczmy
. Oznaczmy ![]() Wówczas dla ciągu
Wówczas dla ciągu ![]() wygenerowanego przy pomocy metody największego spadku z regułą minimalizacji mamy
wygenerowanego przy pomocy metody największego spadku z regułą minimalizacji mamy
zaś dla reguły minimalizacji ograniczonej
gdzie
Dowód
Rozważmy przypadek reguły minimalizacji bez ograniczeń. Z faktu, że ![]() dla każdego
dla każdego ![]() wynika, że
wynika, że ![]() . Na mocy wzoru Taylora, dla
. Na mocy wzoru Taylora, dla ![]() , gdzie
, gdzie ![]() , mamy
, mamy
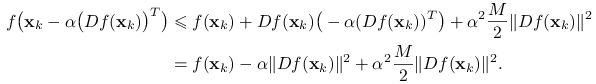 |
(13.2) |
Minimum po prawej stronie przyjmowane jest dla ![]() Przypomnijmy również, że
Przypomnijmy również, że ![]() realizuje minimum po
realizuje minimum po ![]() z lewej strony. Zatem
z lewej strony. Zatem
Odejmijmy od obu stron ![]() i zastosujmy nierówność
i zastosujmy nierówność ![]() wynikającą z lematu 13.1:
wynikającą z lematu 13.1:
Po prostym przekształceniu dostajemy tezę.
Zajmijmy się regułą minimalizacji ograniczonej. Wówczas ![]() realizuje minimum po lewej stronie (13.2) dla
realizuje minimum po lewej stronie (13.2) dla ![]() Minimum po prawej stronie przy ograniczeniu
Minimum po prawej stronie przy ograniczeniu ![]() realizowane jest przez
realizowane jest przez ![]() , patrz rys. 13.1. Postępując teraz identycznie jak powyżej dostajemy tezę.
, patrz rys. 13.1. Postępując teraz identycznie jak powyżej dostajemy tezę.
Podsumujmy. Na mocy lematu 13.1 wiemy, że warunek końca sformułowany jako ograniczenie na normę gradientu funkcji ![]() jest poprawny i daje ograniczenia zarówno na odległość przybliżenia
jest poprawny i daje ograniczenia zarówno na odległość przybliżenia ![]() od punktu minimum, jak i na dokładność wyznaczenia wartości minimalnej funkcji. Zwróćmy uwagę, że czym ”bardziej” ściśle wypukła jest funkcja na otoczeniu
od punktu minimum, jak i na dokładność wyznaczenia wartości minimalnej funkcji. Zwróćmy uwagę, że czym ”bardziej” ściśle wypukła jest funkcja na otoczeniu ![]() , tj. czym większe
, tj. czym większe ![]() , tym ostrzejsza zależność między normą gradientu a odległością od punktu
, tym ostrzejsza zależność między normą gradientu a odległością od punktu ![]() . Lemat 13.2 sugeruje, że zbieżność wartości funkcji jest najszybsza, jeśli funkcja podobnie zachowuje się we wszystkich kierunkach, czyli wartości własne macierzy drugich pochodnych leżą dość blisko siebie. Wówczas iloraz
. Lemat 13.2 sugeruje, że zbieżność wartości funkcji jest najszybsza, jeśli funkcja podobnie zachowuje się we wszystkich kierunkach, czyli wartości własne macierzy drugich pochodnych leżą dość blisko siebie. Wówczas iloraz ![]() jest największy, co korzystnie wpływa na współczynnik kontrakcji
jest największy, co korzystnie wpływa na współczynnik kontrakcji ![]() . A zatem algorytm największego spadku, podobnie jak wszystkie inne metody spadkowe, będzie najlepiej pracował na takich funkcjach, które mają stosunkowo duży iloraz
. A zatem algorytm największego spadku, podobnie jak wszystkie inne metody spadkowe, będzie najlepiej pracował na takich funkcjach, które mają stosunkowo duży iloraz ![]() , lub inaczej,
, lub inaczej, ![]() jest tego samego rzędu co
jest tego samego rzędu co ![]() .
.
13.2. Reguła Armijo
Przypomnijmy regułę Armijo. Kładziemy ![]() , gdzie
, gdzie ![]() jest najmniejszą liczbą całkowitą nieujemną
jest najmniejszą liczbą całkowitą nieujemną ![]() spełniającą nierówność
spełniającą nierówność
Stała ![]() nazywana jest krokiem,
nazywana jest krokiem, ![]() reguluje szybkość zmniejszania kroku (czym mniejsza wartość, tym szybciej krok się zmniejsza), zaś
reguluje szybkość zmniejszania kroku (czym mniejsza wartość, tym szybciej krok się zmniejsza), zaś ![]() odpowiedzialna jest za ostrość warunku: mniejsza wartość osłabia warunek. Zauważmy, że w przypadku metody największego spadku warunek powyższy upraszcza się nieznacznie, ponieważ
odpowiedzialna jest za ostrość warunku: mniejsza wartość osłabia warunek. Zauważmy, że w przypadku metody największego spadku warunek powyższy upraszcza się nieznacznie, ponieważ ![]() :
:
| (13.3) |
Implementacja metody Armijo jest bardzo łatwa. Startujemy z punktu ![]() i sprawdzamy, czy spełniony jest w nim warunek (13.3). Jeśli tak, to kończymy poszukiwanie. W przeciwnym przypadku, rozważamy punkty
i sprawdzamy, czy spełniony jest w nim warunek (13.3). Jeśli tak, to kończymy poszukiwanie. W przeciwnym przypadku, rozważamy punkty ![]() W zadaniu 13.3 pokażemy, że w skończonej liczbie kroków znajdziemy punkt spełniający warunek (13.3), jeśli
W zadaniu 13.3 pokażemy, że w skończonej liczbie kroków znajdziemy punkt spełniający warunek (13.3), jeśli ![]() . Z nierówności (13.3) wynika, że
. Z nierówności (13.3) wynika, że ![]()
Twierdzenie 13.2
Niech ![]() będzie ciągiem punktów skonstruowanych przez zastosowanie metody najmniejszego spadku z regułą Armijo.
będzie ciągiem punktów skonstruowanych przez zastosowanie metody najmniejszego spadku z regułą Armijo.
Jeśli istnieje punkt skupienia
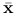 tego ciągu, to jest on punktem krytycznym.
tego ciągu, to jest on punktem krytycznym.Jeśli
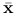 jest punktem krytycznym i macierz
jest punktem krytycznym i macierz 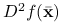 jest dodatnio określona, to istnieje kula
jest dodatnio określona, to istnieje kula 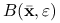 o środku
o środku 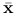 i promieniu
i promieniu 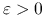 , taka że gdy
, taka że gdy 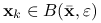 dla pewnego
dla pewnego 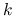 , to ciąg
, to ciąg 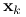 dąży do
dąży do 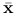 . W szczególności, jeśli w punkcie skupienia
. W szczególności, jeśli w punkcie skupienia 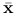 macierz drugich pochodnych jest dodatnio określona, to cały ciąg zmierza do
macierz drugich pochodnych jest dodatnio określona, to cały ciąg zmierza do 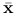 .
.
Dowód
Dowód pierwszej tezy jest niemal identyczny jak dowód twierdzenia 13.1.
Z faktu, że macierz ![]() jest dodatnio określona wynika, że istnieje kula otwarta
jest dodatnio określona wynika, że istnieje kula otwarta ![]() o środku
o środku ![]() , taka że
, taka że ![]() jest wypukła w
jest wypukła w ![]() . Możemy również znaleźć kulę otwartą
. Możemy również znaleźć kulę otwartą ![]() o środku w
o środku w ![]() i mniejszym promieniu niż
i mniejszym promieniu niż ![]() , taką że
, taką że ![]() , jeśli
, jeśli ![]() . Wynika to z ciągłości pochodnej
. Wynika to z ciągłości pochodnej ![]() wokół
wokół ![]() i z tego, że się ona w
i z tego, że się ona w ![]() zeruje. Ciągłość funkcji
zeruje. Ciągłość funkcji ![]() pozwala nam wywnioskować, że istnieje zbiór poziomicowy
pozwala nam wywnioskować, że istnieje zbiór poziomicowy ![]() , dla pewnego
, dla pewnego ![]() , zawarty w
, zawarty w ![]() (zwróć uwagę, że do
(zwróć uwagę, że do ![]() wybieramy punkty z większego zbioru
wybieramy punkty z większego zbioru ![]() , lecz wymagamy by po zastosowaniu warunktu poziomicowego
, lecz wymagamy by po zastosowaniu warunktu poziomicowego ![]() było zawarte w
było zawarte w ![]() ). Zbiór
). Zbiór ![]() ma niepuste wnętrze, bo funkcja
ma niepuste wnętrze, bo funkcja ![]() jest ciągła i
jest ciągła i ![]() . Ponadto jest on oddzielony od brzegu
. Ponadto jest on oddzielony od brzegu ![]() , bo
, bo ![]() ma mniejszy promień. Innymi słowy, jeśli odcinek łączy punkt w
ma mniejszy promień. Innymi słowy, jeśli odcinek łączy punkt w ![]() z punktem spoza
z punktem spoza ![]() , to na tym odcinku jest taki punkt
, to na tym odcinku jest taki punkt ![]() , że
, że ![]() . Wykorzystamy to zaraz. Niech
. Wykorzystamy to zaraz. Niech ![]() . Wówczas
. Wówczas ![]() (bo
(bo ![]() ) oraz
) oraz ![]() . Jeśli teraz
. Jeśli teraz ![]() nie zawiera się w
nie zawiera się w ![]() , to, jak ustaliliśmy powyżej, na odcinku łączącym
, to, jak ustaliliśmy powyżej, na odcinku łączącym ![]() z
z ![]() musi istnieć punkt
musi istnieć punkt ![]() taki że
taki że ![]() . Ale cały ten odcinek leży w
. Ale cały ten odcinek leży w ![]() , na którym to zbiorze funkcja
, na którym to zbiorze funkcja ![]() jest wypukła. Nie może więc istnieć na tym odcinku punkt
jest wypukła. Nie może więc istnieć na tym odcinku punkt ![]() , w którym wartość jest większa niż w obu jego końcach. Sprzeczność! Wykazaliśmy tym samym, że
, w którym wartość jest większa niż w obu jego końcach. Sprzeczność! Wykazaliśmy tym samym, że ![]() . Czyli od pewnego miejsca ciąg
. Czyli od pewnego miejsca ciąg ![]() pozostaje w
pozostaje w ![]() . Jako, że
. Jako, że ![]() jest zwarty, to każdy podciąg
jest zwarty, to każdy podciąg ![]() ma w nim punkt skupienia. Z pierwszej częsci twierdzenia wynika, że jest to punkt krytyczny, a takowy może być tylko jeden w
ma w nim punkt skupienia. Z pierwszej częsci twierdzenia wynika, że jest to punkt krytyczny, a takowy może być tylko jeden w ![]() – jest nim
– jest nim ![]() . Udowodniliśmy więc drugą część twierdzenia.
. Udowodniliśmy więc drugą część twierdzenia.
Poprawność warunku stopu algorytmu pozostaje w mocy, gdyż Lemat 13.1 nie zależy od metody optymalizacyjnej. Teza lematu 13.2 wymaga pewnych zmian, pozostawiając jednak wykładniczą zbieżność (patrz zadanie 13.4).
Jakie zatem są zalety reguły Armijo? Otóż, jak wspomniane zostało wyżej, jest ona prosta w implementacji i nie wymaga stosowania metod optymalizacji funkcji jednej zmiennej. Koszt tego uproszczenia nie jest zwykle również duży, lecz zależy od parametrów ![]() Nie ma niestety reguł doboru tych parametrów – pozostawia się to doświadczeniu i intuicji użytkownika.
Nie ma niestety reguł doboru tych parametrów – pozostawia się to doświadczeniu i intuicji użytkownika.
13.3. Zadania
Ćwiczenie 13.1
Udowodnij, że jeśli ![]() jest kierunkiem spadku w punkcie
jest kierunkiem spadku w punkcie ![]() , to istnieje
, to istnieje ![]() , taka że dla
, taka że dla ![]() mamy
mamy
Ćwiczenie 13.2
Udowodnij lemat 13.1.
Przyjrzyj się dokładnie dowodowi lematu 12.4.
Ćwiczenie 13.3
Wykaż, że jeśli ![]() , to wartość
, to wartość ![]() z reguły Armijo można wyznaczyć w skończonej liczbie kroków (choć różnej dla każdego
z reguły Armijo można wyznaczyć w skończonej liczbie kroków (choć różnej dla każdego ![]() ).
).
Rozważ funkcję ![]() Zastanów się, dlaczego teza nie jest poprawna dla
Zastanów się, dlaczego teza nie jest poprawna dla ![]() .
.
Ćwiczenie 13.4
Zmodyfikuj tezę i dowód lematu 13.2 tak, aby stosował się on do metody Armijo.
Ćwiczenie 13.5
Udowodnij, że w metodzie największego spadku z regułą minimalizacji (bez ograniczenia) kolejne kierunki ![]() są do siebie prostopadłe.
są do siebie prostopadłe.