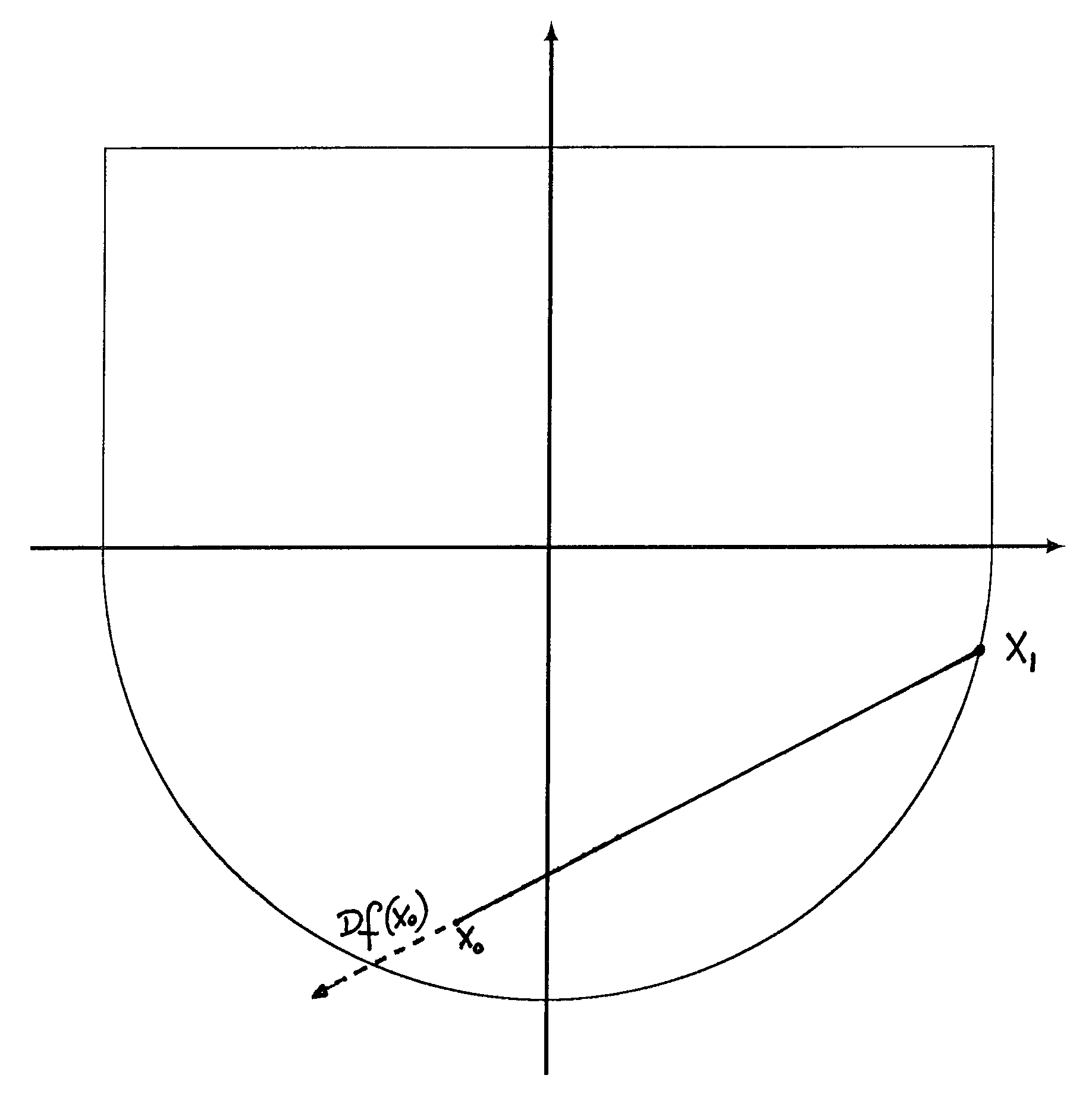Zagadnienia
14. Metody optymalizacji z ograniczeniami
W tym rozdziale skupimy się na metodach numerycznych rozwiązywania problemów optymalizacyjnych z ograniczeniami nierównościowymi. Pokażemy problemy z zastosowaniem metody największego spadku i jej naiwnych modyfikacji oraz zaproponujemy skuteczne aczkolwiek bardziej skomplikowane podejście.
Problem optymalizacyjny na następującą postać:
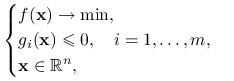 |
(14.1) |
gdzie ![]() . A zatem zbiór punktów dopuszczalnych jest zadany przez
. A zatem zbiór punktów dopuszczalnych jest zadany przez
| (14.2) |
W rozważaniach tego rozdziału będziemy odwoływać się często do pojęcia zbioru kierunków dopuszczalnych zdefiniowanego następująco
14.1. Algorytm Zoutendijk'a dla ograniczeń liniowych
Rozważmy bardzo prostą modyfikację algorytmu największego spadku. Otóż jeśli punkt znajduje się wewnątrz zbioru ![]() , to istnieje możliwość poruszania się wzdłuż kierunku największego spadku aż do uderzenia w brzeg. Jeśli punkt już jest na brzegu, to naturalne jest wybrać taki kierunek ruchu, by pozwalał on na jak największy spadek wartości funkcji celu a jednocześnie na ruch w jego kierunku. Kierunek taki nazywamy dopuszczalnym kierunkiem spadku w punkcie
, to istnieje możliwość poruszania się wzdłuż kierunku największego spadku aż do uderzenia w brzeg. Jeśli punkt już jest na brzegu, to naturalne jest wybrać taki kierunek ruchu, by pozwalał on na jak największy spadek wartości funkcji celu a jednocześnie na ruch w jego kierunku. Kierunek taki nazywamy dopuszczalnym kierunkiem spadku w punkcie ![]() i definiujemy jako kierunek dopuszczalny
i definiujemy jako kierunek dopuszczalny ![]() , taki że
, taki że ![]()
Okazuje się, że pomysł ten działa całkiem dobrze, jeśli ograniczenia są liniowe i nosi nazwę algorytm Zoutendijk'a. Przypomnijmy, że liniowość ograniczeń znacznie upraszcza problem, co pozwoli nam na rozszerzenie analizy w tym podrozdziale do zagadnień z ograniczeniami nierównościowymi i równościowymi, tzn.
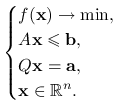 |
(14.3) |
Tutaj ![]() jest macierzą
jest macierzą ![]() ,
, ![]() jest macierzą
jest macierzą ![]() , zaś
, zaś ![]() i
i ![]() Poniższy lemat charakteryzuje zbiór dopuszczalnych kierunków spadku. Jego dowód pozostawiamy jako ćwiczenie.
Poniższy lemat charakteryzuje zbiór dopuszczalnych kierunków spadku. Jego dowód pozostawiamy jako ćwiczenie.
Lemat 14.1
Niech ![]() będzie punktem dopuszczalnym dla zagadnienia (14.3) i załóżmy, że macierz
będzie punktem dopuszczalnym dla zagadnienia (14.3) i załóżmy, że macierz ![]() i wektor
i wektor ![]() mogą być podzielone w zależności od aktywności ograniczeń na
mogą być podzielone w zależności od aktywności ograniczeń na ![]() ,
, ![]() i
i ![]() (z dokładnością do przenumerowania ograniczeń), tzn.
(z dokładnością do przenumerowania ograniczeń), tzn. ![]() oraz
oraz ![]() Wektor
Wektor ![]() jest kierunkiem dopuszczalnym w
jest kierunkiem dopuszczalnym w ![]() , jeśli
, jeśli ![]() oraz
oraz ![]() Jeśli, ponadto,
Jeśli, ponadto, ![]() , to
, to ![]() jest dopuszczalnym kierunkiem spadku.
jest dopuszczalnym kierunkiem spadku.
Jak wybrać najlepszy dopuszczalny kierunek spadku w punkcie ![]() ? Najprościej byłoby rozwiązać zagadnienie
? Najprościej byłoby rozwiązać zagadnienie
| (14.4) |
Ograniczenie na normę wektora ![]() jest konieczne. Jeśli byśmy je opuścili, to dla dowolnego dopuszczalnego kierunku spadku
jest konieczne. Jeśli byśmy je opuścili, to dla dowolnego dopuszczalnego kierunku spadku ![]() jego wielokrotność
jego wielokrotność ![]() ,
, ![]() , jest również kierunkiem spadku. Co więcej,
, jest również kierunkiem spadku. Co więcej, ![]() , czyli
, czyli ![]() i problem powyższy nie ma jednoznacznego rozwiązania.
i problem powyższy nie ma jednoznacznego rozwiązania.
Korzystając z lematu 14.1 powyższe zagadnienie (14.4) można wyrazić jako
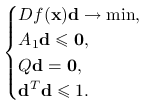 |
Zauważmy, że jedyna nieliniowość związana jest z ograniczeniem na normę wektora ![]() . W praktyce, bez większych strat dla jakości algorytmu, zamienia się ją na ograniczenia liniowe, które pozwalają skorzystać z szybkich metod optymalizacji liniowej (np. algorytmu sympleks – patrz monografie Bazaraa, Jarvis'a, Shetty [2], Gass'a [8] lub Luenberger'a [9]). Najpopularniejsze są następujące dwa zamienniki normy euklidesowej
. W praktyce, bez większych strat dla jakości algorytmu, zamienia się ją na ograniczenia liniowe, które pozwalają skorzystać z szybkich metod optymalizacji liniowej (np. algorytmu sympleks – patrz monografie Bazaraa, Jarvis'a, Shetty [2], Gass'a [8] lub Luenberger'a [9]). Najpopularniejsze są następujące dwa zamienniki normy euklidesowej ![]() :
:
norma
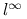 , tzn.
, tzn. 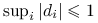 , co zapisuje się jako
, co zapisuje się jako
norma
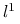 , tzn.
, tzn. 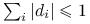 , co zapisuje się jako
, co zapisuje się jako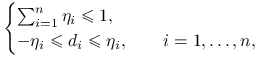
gdzie
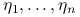 są nowymi zmiennymi (pomocniczymi).
są nowymi zmiennymi (pomocniczymi).
Oto pełny algorytm:
Inicjalizacja: Wybierz punkt początkowy
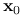 .
.Krok
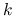 -ty:
-ty:Wybierz kierunek ruchu
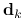 jako rozwiązanie problemu optymalizacyjnego:
jako rozwiązanie problemu optymalizacyjnego: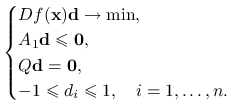
(14.5) Jeśli
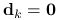 , to zakończ działanie algorytmu. Punkt
, to zakończ działanie algorytmu. Punkt 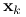 spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.
spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.Połóż
![\alpha _{k}=\text{argmin}_{{\alpha\in[0,A_{k}]}}f(\mathbf{x}_{k}+\alpha\mathbf{d}_{k})](wyklady/op2/mi/mi2023.png) , gdzie
, gdzie 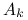 jest największą liczbą o tej własności, że odcinek łączący
jest największą liczbą o tej własności, że odcinek łączący 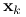 i
i 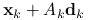 zawarty jest w
zawarty jest w 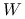 .
.Połóż
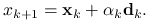
Przyjrzyjmy się jeszcze raz wyborowi kierunku ![]() . Wektor
. Wektor ![]() spełnia wszystkie ograniczenia, a zatem optymalna wartość funkcji celu
spełnia wszystkie ograniczenia, a zatem optymalna wartość funkcji celu ![]() jest co najwyżej równa zeru. Wówczas punkt
jest co najwyżej równa zeru. Wówczas punkt ![]() spełnia warunek konieczny pierwszego rzędu, czego dowodzimy w poniższym lemacie.
spełnia warunek konieczny pierwszego rzędu, czego dowodzimy w poniższym lemacie.
Lemat 14.2
W ![]() spełniony jest warunek konieczny pierwszego rzędu wtw, gdy
spełniony jest warunek konieczny pierwszego rzędu wtw, gdy ![]() .
.
Dowód
Przypomnijmy najpierw notację. Przez ![]() oznaczamy stożek kierunków spadku, tzn.
oznaczamy stożek kierunków spadku, tzn.
zaś przez ![]() – stożek kierunków stycznych dla ograniczeń zlinearyzowanych w punkcie
– stożek kierunków stycznych dla ograniczeń zlinearyzowanych w punkcie ![]() , który dla ograniczeń liniowych danych jest wzorem
, który dla ograniczeń liniowych danych jest wzorem
Zauważmy, że ![]() jest rozwiązaniem zagadnienia (14.5) wtw, gdy
jest rozwiązaniem zagadnienia (14.5) wtw, gdy ![]() . Postępując dalej jak w dowodzie twierdzenia 8.1 dostajemy implikację w lewo. Implikacja w drugą stronę wynika faktu, że na mocy lematu Farkasa, lemat 5.3, istnienie rozwiązania (8.5) pociąga brak rozwiązania (8.4), co jest równoważne temu, że
. Postępując dalej jak w dowodzie twierdzenia 8.1 dostajemy implikację w lewo. Implikacja w drugą stronę wynika faktu, że na mocy lematu Farkasa, lemat 5.3, istnienie rozwiązania (8.5) pociąga brak rozwiązania (8.4), co jest równoważne temu, że ![]()
14.2. Algorytm Zoutendijk'a dla ograniczeń nieliniowych
Zastanówmy się, czy algorytm Zoutendijk'a działa równie dobrze dla ograniczeń nieliniowych:
Inicjalizacja: Wybierz punkt początkowy
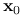 .
.Krok
 -ty:
-ty:Wybierz kierunek ruchu
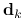 jako rozwiązanie problemu optymalizacyjnego:
jako rozwiązanie problemu optymalizacyjnego: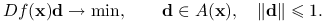
Jeśli
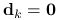 , to zakończ działanie algorytmu. Punkt
, to zakończ działanie algorytmu. Punkt 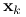 spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.
spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.Połóż
![\alpha _{k}=\text{argmin}_{{\alpha\in[0,A_{k}]}}f(\mathbf{x}_{k}+\alpha\mathbf{d}_{k})](wyklady/op2/mi/mi2023.png) , gdzie
, gdzie 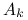 jest największą liczbą o tej własności, że odcinek łączący
jest największą liczbą o tej własności, że odcinek łączący 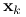 i
i 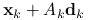 zawarty jest w
zawarty jest w 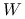 .
.Połóż
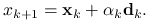
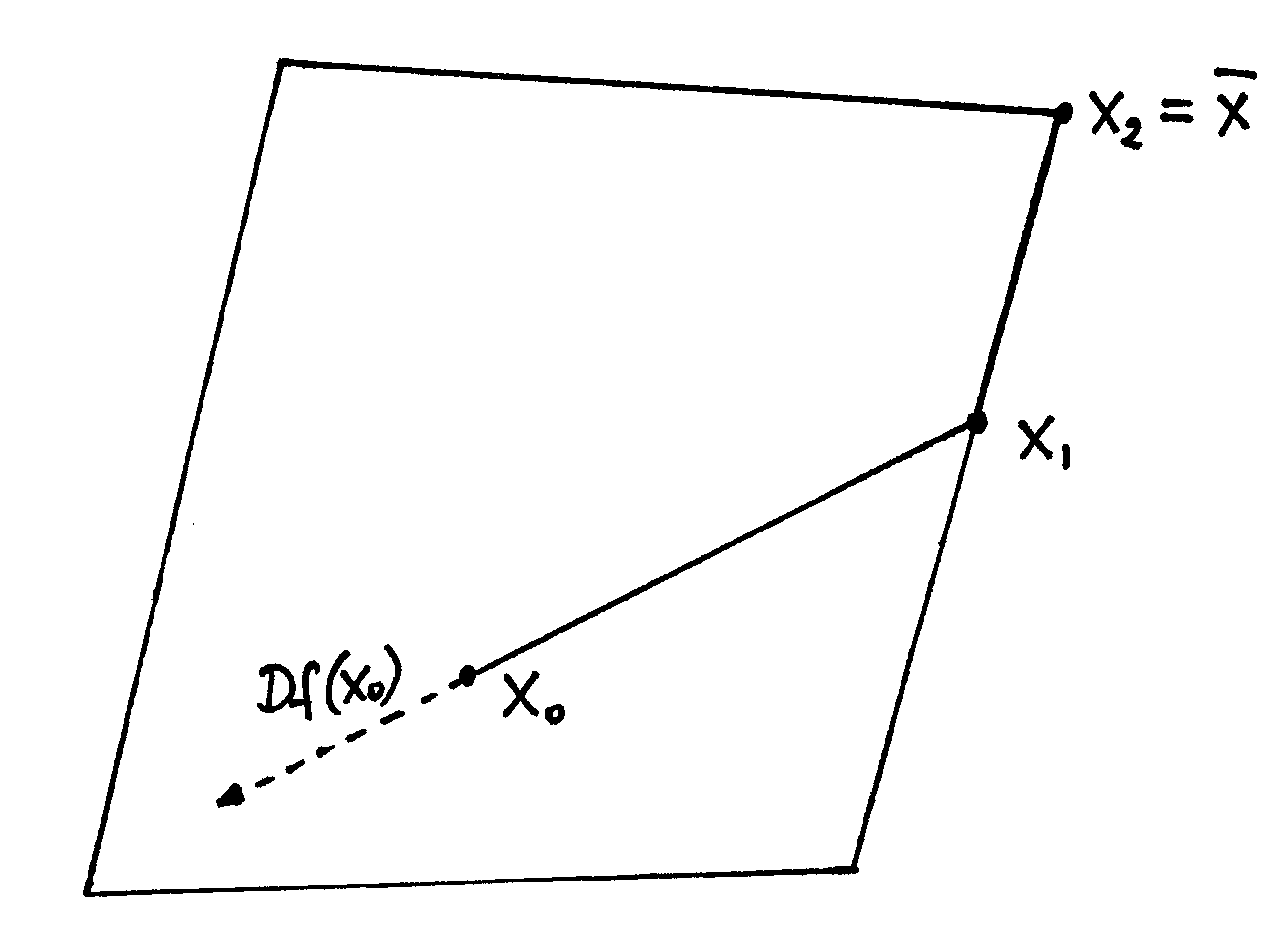
W poniższych przykładach rozważamy minimalizowanie funkcji ![]() na różnych zbiorach. Punkt minimum oznaczamy zawsze przez
na różnych zbiorach. Punkt minimum oznaczamy zawsze przez ![]() . Na rysunku 14.1 widać, że już w kroku drugim osiągamy minimum. Jeśli zbiór
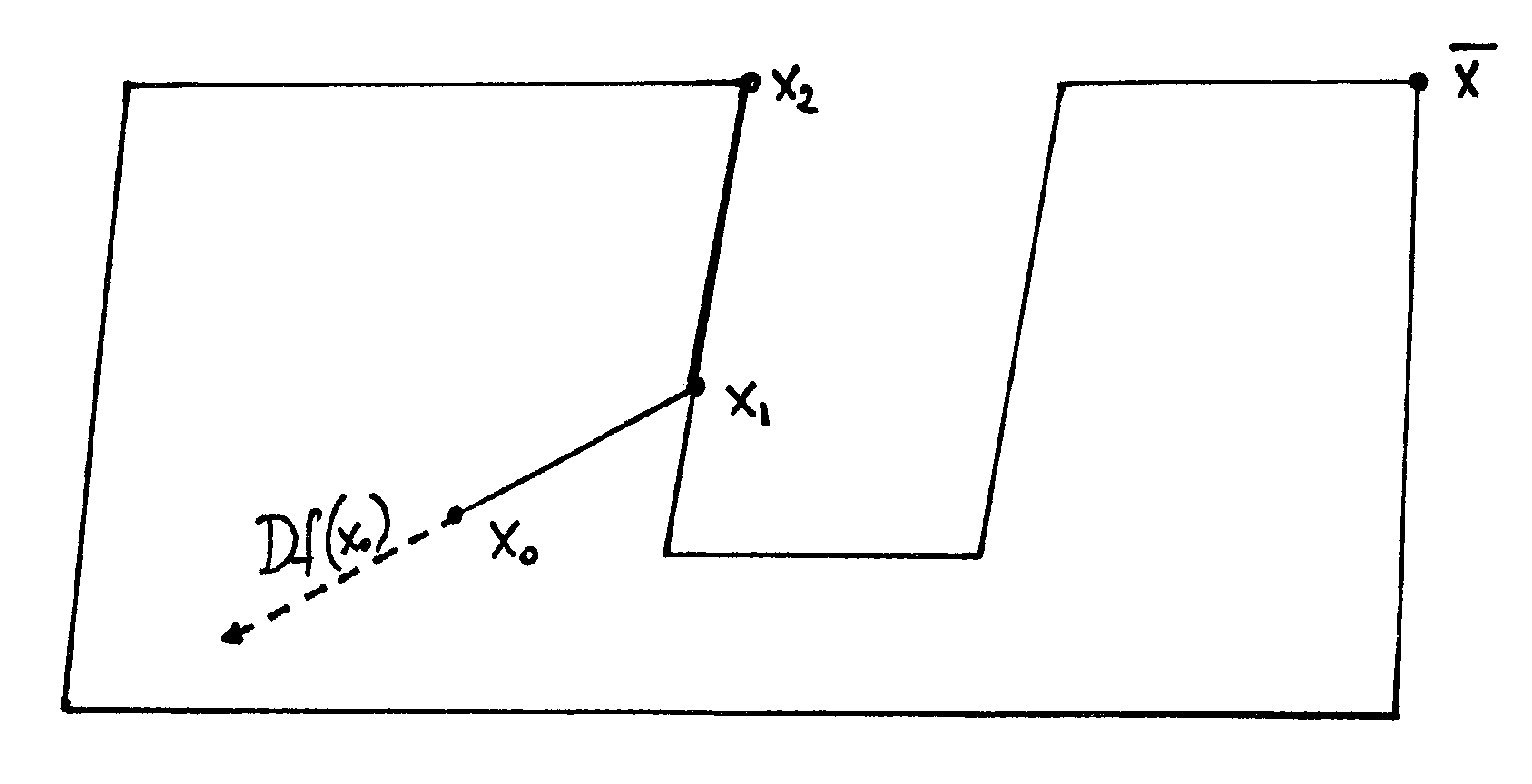
. Na rysunku 14.1 widać, że już w kroku drugim osiągamy minimum. Jeśli zbiór ![]() nie jest wypukły algorytm prowadzi nas w kozi róg, z którego już nie możemy się uwolnić, patrz 14.2. Jest to niestety cecha wszystkich algorytmów tego typu, więc musimy zawsze wymagać, by zbiór punktów dopuszczalnych był wypukły. Czy to już wystarczy? Niestety nie. Na rysunku 14.3 możemy zobaczyć, że nawet w przypadku zbioru wypukłego algorytm nie działa. Problem wyboru kierunku
nie jest wypukły algorytm prowadzi nas w kozi róg, z którego już nie możemy się uwolnić, patrz 14.2. Jest to niestety cecha wszystkich algorytmów tego typu, więc musimy zawsze wymagać, by zbiór punktów dopuszczalnych był wypukły. Czy to już wystarczy? Niestety nie. Na rysunku 14.3 możemy zobaczyć, że nawet w przypadku zbioru wypukłego algorytm nie działa. Problem wyboru kierunku ![]() nie ma rozwiązania, gdyż zbiór
nie ma rozwiązania, gdyż zbiór ![]() nie jest domknięty. Intuicyjnie łatwo jest podać rozwiązanie tego problemu. Należy wybrać taki kierunek
nie jest domknięty. Intuicyjnie łatwo jest podać rozwiązanie tego problemu. Należy wybrać taki kierunek ![]() , aby nie tylko spadek był jak największy, ale również, żeby dość duży fragment półprostej poprowadzonej w tym kierunku zawierał się w zbiorze
, aby nie tylko spadek był jak największy, ale również, żeby dość duży fragment półprostej poprowadzonej w tym kierunku zawierał się w zbiorze ![]() . Co więcej, zależy nam na prostocie, czytaj liniowości, zagadnienia optymalizacyjnego wyznaczającego kierunek
. Co więcej, zależy nam na prostocie, czytaj liniowości, zagadnienia optymalizacyjnego wyznaczającego kierunek ![]() . Rozwiązanie podpowiada następujący lemat, którego dowód pozostawiamy jako ćwiczenie.
. Rozwiązanie podpowiada następujący lemat, którego dowód pozostawiamy jako ćwiczenie.
Lemat 14.3
Niech ![]() będzie punktem dopuszczalnym. Jeśli
będzie punktem dopuszczalnym. Jeśli ![]() ,
, ![]() są różniczkowalne w
są różniczkowalne w ![]() i
i ![]() ,
, ![]() są ciągłe w
są ciągłe w ![]() , to kierunek
, to kierunek ![]() spełniający
spełniający ![]() i
i ![]() ,
, ![]() , jest dopuszczalnym kierunkiem spadku.
, jest dopuszczalnym kierunkiem spadku.
Lemat powyższy podaje tylko warunek dostateczny. Łatwo znaleźć przykład zagadnienia optymalizacyjnego z ograniczeniami nierównościowymi, dla którego jeden z dopuszczalnym kierunków spadku nie spełnia założeń lematu (ćwiczenie 14.5).
Znalezienie wektora ![]() spełniającego
spełniającego ![]() i
i ![]() ,
, ![]() sprowadza się do rozwiązania zagadnienia
sprowadza się do rozwiązania zagadnienia
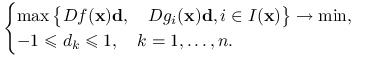 |
Trudną w implementacji funkcję celu można sprowadzić do znacznie prostszej formy problemu optymalizacji liniowej:
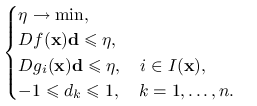 |
(14.6) |
Optymalizacji dokonuje się tutaj względem dwóch zmiennych: ![]() oraz
oraz ![]() Zauważmy, że
Zauważmy, że ![]() , gdyż para
, gdyż para ![]() ,
, ![]() rozwiązuje powyższy układ. Jeśli wartość funkcji celu jest mniejsza od zera, to, na mocy lematu 14.1, rozwiązanie jest dopuszczalnym kierunkiem spadku. Jeśli
rozwiązuje powyższy układ. Jeśli wartość funkcji celu jest mniejsza od zera, to, na mocy lematu 14.1, rozwiązanie jest dopuszczalnym kierunkiem spadku. Jeśli ![]() jest rozwiązaniem i w punkcie
jest rozwiązaniem i w punkcie ![]() spełniony jest warunek liniowej niezależności ograniczeń, to wówczas w
spełniony jest warunek liniowej niezależności ograniczeń, to wówczas w ![]() zachodzi warunek konieczny pierwszego rzędu. Prawdziwa jest również odwrotna implikacja.
zachodzi warunek konieczny pierwszego rzędu. Prawdziwa jest również odwrotna implikacja.
Lemat 14.4
Jeśli w punkcie dopuszczalnym ![]() spełniony jest warunek liniowej niezależności ograniczeń i rozwiązaniem problemu (14.6) jest
spełniony jest warunek liniowej niezależności ograniczeń i rozwiązaniem problemu (14.6) jest ![]() , to w
, to w ![]() zachodzi warunek konieczny pierwszego rzędu. I odwrotnie, jeśli w
zachodzi warunek konieczny pierwszego rzędu. I odwrotnie, jeśli w ![]() spełniony jest warunek konieczny pierwszego rzędu, to rozwiązaniem (14.6) jest
spełniony jest warunek konieczny pierwszego rzędu, to rozwiązaniem (14.6) jest ![]() (nie jest tu konieczne założenie o regularności punktu
(nie jest tu konieczne założenie o regularności punktu ![]() ).
).
Dowód
Jeśli ![]() jest rozwiązaniem, to układ
jest rozwiązaniem, to układ ![]() , gdzie
, gdzie ![]() składa się wierszowo z gradientów
składa się wierszowo z gradientów ![]() i
i ![]() ,
, ![]() , nie ma rozwiązania. Na mocy lematu 6.2 istnieje
, nie ma rozwiązania. Na mocy lematu 6.2 istnieje ![]() ,
, ![]() , dla którego
, dla którego ![]() . Połóżmy
. Połóżmy ![]() i
i ![]() ,
, ![]() Równość
Równość ![]() zapisać można w następujący sposób:
zapisać można w następujący sposób:
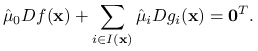 |
Z założenia o liniowej niezależności gradientów ograniczeń aktywnych wnioskujemy, że ![]() . Kładąc
. Kładąc ![]() ,
, ![]() dostajemy wektor mnożników Lagrange'a z warunku koniecznego pierwszego rzędu.
dostajemy wektor mnożników Lagrange'a z warunku koniecznego pierwszego rzędu.
Aby dowieść implikacji odwrotnej, zauważmy, że jeśli w ![]() spełniony jest warunek konieczny pierwszego rzędu, to
spełniony jest warunek konieczny pierwszego rzędu, to ![]() spełnia następujące warunki:
spełnia następujące warunki: ![]() ,
, ![]() i
i ![]() . Na mocy lematu 6.2 nie istnieje
. Na mocy lematu 6.2 nie istnieje ![]() , dla którego
, dla którego ![]() A zatem rozwiązaniem 14.6 jest
A zatem rozwiązaniem 14.6 jest ![]()
Zapiszmy w pełni algorytm zaproponowany przez Zoutendijka dla problemów z nieliniowymi ograniczeniami nierównościowymi:
Inicjalizacja: Wybierz punkt początkowy
 .
.Krok
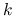 -ty:
-ty:Wybierz kierunek ruchu
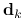 jako rozwiązanie problemu optymalizacyjnego (14.6)
jako rozwiązanie problemu optymalizacyjnego (14.6)
Jeśli
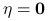 , to zakończ działanie algorytmu. Punkt
, to zakończ działanie algorytmu. Punkt 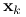 spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.
spełnia warunek konieczny pierwszego rzędu. W przeciwnym przypadku kontynuuj.Połóż
![\alpha _{k}=\text{argmin}_{{\alpha\in[0,A_{k}]}}f(\mathbf{x}_{k}+\alpha\mathbf{d}_{k})](wyklady/op2/mi/mi2023.png) , gdzie
, gdzie 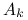 jest największą liczbą o tej własności, że odcinek łączący
jest największą liczbą o tej własności, że odcinek łączący 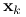 i
i 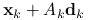 zawarty jest w
zawarty jest w 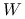 .
.Połóż
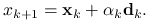
Przykład 14.1
Rozważmy problem optymalizacji z ograniczeniami nieliniowymi:
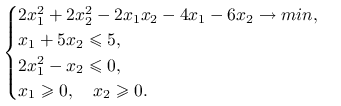 |
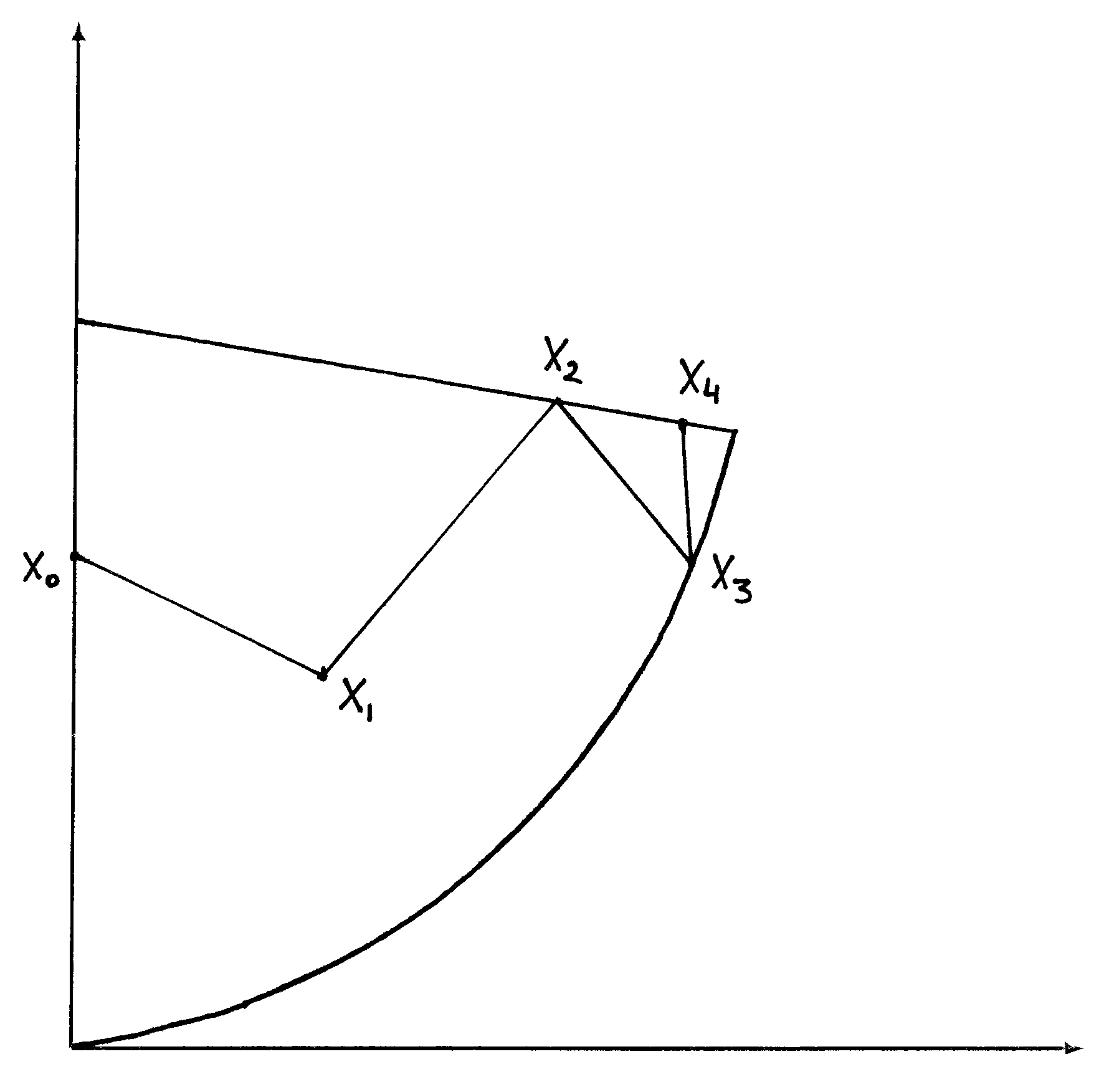
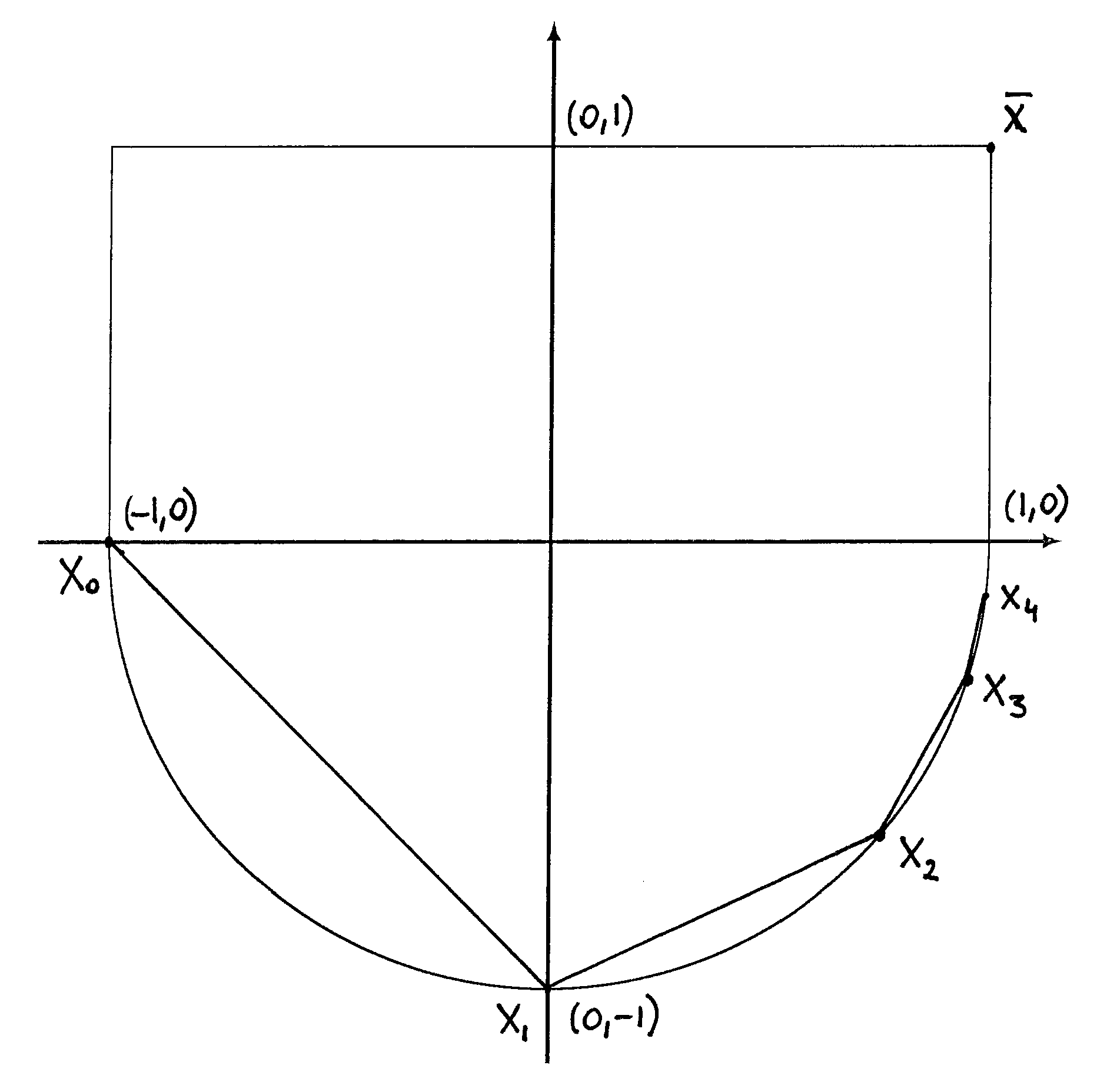
Pokażemy, w jaki sposób postępując iteracje metody Zoutendijka. Weźmy punkt startowy ![]() Dostajemy następujący ciąg punktów:
Dostajemy następujący ciąg punktów:
Widzimy, że ciąg ten dość znacznie oscyluje w zbiorze punktów dopuszczalnych, patrz rys. 14.4. Jest to charakterystyczne zachowanie metody kierunków spadku dla problemów z ograniczeniami.
Algorytm Zoutendijka może polec nawet na dość prostych prostych problemach optymalizacyjnych. Rozważmy minimalizowanie funkcji liniowej ![]() na zbiorze zaznaczonym na rysunku 14.5. Minimum znajduje się w punkcie
na zbiorze zaznaczonym na rysunku 14.5. Minimum znajduje się w punkcie ![]() . Rozpoczynając od punktu
. Rozpoczynając od punktu ![]() , kolejne iteracje algorytmu Zoutendijka wygenerują ciąg punktów zbiegający do
, kolejne iteracje algorytmu Zoutendijka wygenerują ciąg punktów zbiegający do ![]() . Algorytm ten nie pozwoli nam na przybliżenie właściwego rozwiązania
. Algorytm ten nie pozwoli nam na przybliżenie właściwego rozwiązania ![]() . Co więcej, wartość funkcji celu w punkcie
. Co więcej, wartość funkcji celu w punkcie ![]() wynosi
wynosi ![]() , w porównaniu do
, w porównaniu do ![]() W następnym podrozdziale pokażemy jak mała modyfikacja pozwoli naprawić algorytm Zoutendijka.
W następnym podrozdziale pokażemy jak mała modyfikacja pozwoli naprawić algorytm Zoutendijka.
14.3. Modyfikacja Topkis'a-Veinott'a
Topkis i Veinott zaproponowali w roku 1967 niewielką modyfikację wyznaczania kierunku ![]() w algorytmie Zoutendijka:
w algorytmie Zoutendijka:
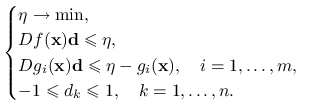 |
(14.7) |
Linia dotycząca warunku na gradienty ograniczeń obejmuje teraz wszystkie ograniczenia. Dla ograniczeń aktywnych, ![]() , mamy
, mamy ![]() , a więc warunki te są identyczne jak w (14.6). W przypadku ograniczeń nieaktywnych
, a więc warunki te są identyczne jak w (14.6). W przypadku ograniczeń nieaktywnych ![]() , czyli prawa strona jest większa niż
, czyli prawa strona jest większa niż ![]() O ile dla dużych wartości
O ile dla dużych wartości ![]() ograniczenie takie jest prawie niezauważalne, to dla ograniczeń, które są ”prawie aktywne”, odgrywa znaczną rolę. Poza tym, z punktu widzenia implementacji, rozwiązuje to kwestię znajdowania zbioru ograniczeń aktywnych (ze względu na niedokładności zapisu liczb, prawie nigdy nie będzie spełniony warunek
ograniczenie takie jest prawie niezauważalne, to dla ograniczeń, które są ”prawie aktywne”, odgrywa znaczną rolę. Poza tym, z punktu widzenia implementacji, rozwiązuje to kwestię znajdowania zbioru ograniczeń aktywnych (ze względu na niedokładności zapisu liczb, prawie nigdy nie będzie spełniony warunek ![]() ).
).
O skuteczności modyfikacji (14.7) świadczy następujące twierdzenie, które podamy bez dowodu:
Twierdzenie 14.1
Załóżmy, że ![]() ,
, ![]() , są klasy
, są klasy ![]() . Jeśli ciąg
. Jeśli ciąg ![]() wygenerowany przez algorytm Zoutendijka z modyfikacją Topkis'a-Veinott'a posiada punkt skupienia, w którym spełniony jest warunek liniowej niezależności, to zachodzi w nim warunek konieczny pierwszego rzędu.
wygenerowany przez algorytm Zoutendijka z modyfikacją Topkis'a-Veinott'a posiada punkt skupienia, w którym spełniony jest warunek liniowej niezależności, to zachodzi w nim warunek konieczny pierwszego rzędu.
14.4. Podsumowanie
Metody numeryczne opisane w tym rozdziale pozwalają na znalezienie aproksymacji punktów, w których spełniony jest warunek konieczny pierwszego rzędu. Twierdzenie 7.6 zagwarantuje dopiero optymalność tych punktów. W szczególności, jeśli ograniczenia są liniowe, to wystarczy założyć pseudowypukłość funkcji ![]() . Zwróćmy uwagę, że wymagaliśmy podobnych założeń w poprzednim rozdziale, dla optymalizacji bez ograniczeń. Wymóg wypukłości okazuje się bardzo naturalnym i, co więcej, koniecznym dla sprawnego działania tych metod.
. Zwróćmy uwagę, że wymagaliśmy podobnych założeń w poprzednim rozdziale, dla optymalizacji bez ograniczeń. Wymóg wypukłości okazuje się bardzo naturalnym i, co więcej, koniecznym dla sprawnego działania tych metod.
14.5. Zadania
Ćwiczenie 14.1
Znajdź graficznie zbiór dopuszczalnych kierunków spadku w punkcie ![]() dla zagadnienia
dla zagadnienia
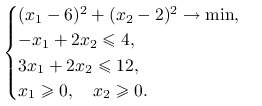 |
Ćwiczenie 14.2
Udowodnij lemat 14.1.
Ćwiczenie 14.3
Rozwiąż następujące zagadnienie optymalizacyjne z ograniczeniami liniowymi:
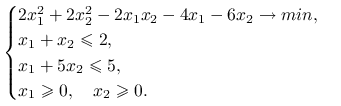 |
Zastosuj algorytm Zoutendijka i weź jako punkt początkowy ![]()
Algorytm kończy się w trzeciej iteracji (optymalna wartość funkcji celu w zagadnieniu poszukiwania kierunku ![]() wynosi wówczas
wynosi wówczas ![]() ).
).
Ćwiczenie 14.4
Udowodnij lemat 14.3.
Ćwiczenie 14.5
Podaj przykład problemu optymalizacyjnego z ograniczeniami nierównościowymi, dla którego istnieje dopuszczalny kierunek spadku, który nie spełnia założeń lematu 14.3.