Zagadnienia
2. Ekstrema funkcji wielu zmiennych
2.1. Notacja i twierdzenia Taylora w wielu wymiarach
W tym podrozdziale przypomnimy krótko twierdzenia Taylora dla funkcji wielu zmiennych. Wprowadźmy najpierw niezbędną notację.
Niech ![]() , gdzie
, gdzie ![]() jest zbiorem otwartym. Przyjmiemy następujące oznaczenia:
jest zbiorem otwartym. Przyjmiemy następujące oznaczenia:
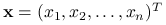 – wektor kolumnowy,
– wektor kolumnowy,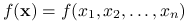 ,
,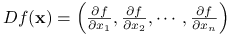 – gradient funkcji
– gradient funkcji  ,
,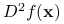 – Hesjan funkcji
– Hesjan funkcji  :
:![D^{2}f(\mathbf{x})=\left(\begin{array}[]{cccc}\frac{\partial^{2}f}{\partial x_{1}^{2}}&\frac{\partial^{2}f}{\partial x_{1}\partial x_{2}}&\cdots&\frac{\partial^{2}f}{\partial x_{1}\partial x_{n}}\\
\frac{\partial^{2}f}{\partial x_{2}\partial x_{1}}&\frac{\partial^{2}f}{\partial x_{2}^{2}}&\cdots&\frac{\partial^{2}f}{\partial x_{2}\partial x_{n}}\\
\vdots&\vdots&\ddots&\\
\frac{\partial^{2}f}{\partial x_{n}\partial x_{1}}&\frac{\partial^{2}f}{\partial x_{n}\partial x_{2}}&\cdots&\frac{\partial^{2}f}{\partial x_{n}^{2}}\\
\end{array}\right).](wyklady/op2/mi/mi293.png)
Definicja 2.1
Funkcja ![]() jest różniczkowalna w punkcie
jest różniczkowalna w punkcie ![]() , jeśli istnieje wektor
, jeśli istnieje wektor ![]() , taki że
, taki że
dla ![]()
Funkcja ![]() jest dwukrotnie różniczkowalna w punkcie
jest dwukrotnie różniczkowalna w punkcie ![]() , jeśli istnieje wektor
, jeśli istnieje wektor ![]() oraz macierz
oraz macierz ![]() , takie że
, takie że
dla ![]()
Uwaga 2.1
Możemy założyć, że macierz ![]() w powyższej definicji jest symetryczna. Wystarczy zauważyć, że
w powyższej definicji jest symetryczna. Wystarczy zauważyć, że
Twierdzenie 2.1
![]()
I) Jeśli funkcja
 jest różniczkowalna w
jest różniczkowalna w 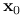 , to
, to 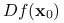 istnieje i
istnieje i 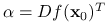 . Odwrotnie, jeśli
. Odwrotnie, jeśli 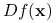 istnieje w pewnym otoczeniu
istnieje w pewnym otoczeniu 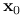 i jest ciągłe w
i jest ciągłe w 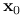 , to
, to  jest różniczkowalna w
jest różniczkowalna w 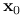 .
.
II) Jeśli hesjan
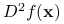 istnieje w pewnym otoczeniu
istnieje w pewnym otoczeniu 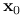 i jest ciągły w
i jest ciągły w 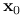 , to
, to  jest dwukrotnie różniczkowalna w
jest dwukrotnie różniczkowalna w 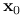 ,
, 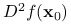 jest macierzą symetryczną oraz
jest macierzą symetryczną oraz 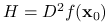 .
.
Dowód powyższego twierdzenia pomijamy. Zainteresowany czytelnik znajdzie go w podręcznikach analizy wielowymiarowej.
Uwaga 2.2
Ilekroć będziemy chcieli wykorzystać drugą pochodną funkcji wielowymiarowej, bedziemy musieli zakładać, że hesjan ![]() jest funkcją ciągłą. Jeśli nie poczynimy takiego założenia, nie będziemy mieli dobrego sposobu na policzenie drugiej pochodnej, a zatem taki rezultat będzie miał małą wartość praktyczną.
jest funkcją ciągłą. Jeśli nie poczynimy takiego założenia, nie będziemy mieli dobrego sposobu na policzenie drugiej pochodnej, a zatem taki rezultat będzie miał małą wartość praktyczną.
Uwaga 2.3
Dla funkcji ![]() określonej na zbiorze otwartym
określonej na zbiorze otwartym ![]() mówimy, że
mówimy, że ![]() jest klasy
jest klasy ![]() (odpowiednio, klasy
(odpowiednio, klasy ![]() ) i piszemy
) i piszemy ![]() (
(![]() ), gdy
), gdy
![]() jest ciągła na
jest ciągła na ![]() oraz
oraz ![]() (odpowiednio,
(odpowiednio, ![]() i
i ![]() ) istnieją
i są ciągłe na
) istnieją
i są ciągłe na ![]() . Gdy rozważany zbiór
. Gdy rozważany zbiór ![]() nie jest otwarty, mówimy że
nie jest otwarty, mówimy że ![]() jest klasy
jest klasy
![]() (odpowiednio, klasy
(odpowiednio, klasy ![]() ) na
) na ![]() , jeśli istnieje
rozszerzenie
, jeśli istnieje
rozszerzenie ![]() funkcji
funkcji ![]() do zbioru otwartego
do zbioru otwartego ![]() zawierającego
zawierającego ![]() takie, że
takie, że ![]() jest klasy
jest klasy ![]() (odpowiednio, klasy
(odpowiednio, klasy ![]() ) na
) na ![]() . W tym wypadku można więc mówić o pochodnych cząstkowych funkcji
. W tym wypadku można więc mówić o pochodnych cząstkowych funkcji ![]() również w
punktach brzegowych zbioru
również w
punktach brzegowych zbioru ![]() . Pochodne te są jednoznacznie określone przez wartości funkcji na
. Pochodne te są jednoznacznie określone przez wartości funkcji na ![]() , jeśli
zachodzi
, jeśli
zachodzi ![]() (wynika to z ciągłości tych pochodnych).
(wynika to z ciągłości tych pochodnych).
Zapiszemy teraz rozwinięcie Taylora rzędu ![]() .
.
Lemat 2.1
Niech ![]() otwarty. Dla funkcji
otwarty. Dla funkcji ![]() klasy
klasy ![]() i punktów
i punktów ![]() takich, że odcinek łączący
takich, że odcinek łączący ![]() z
z ![]() leży w
leży w ![]() zachodzi
zachodzi
gdzie ![]() jest pewnym punktem wewnątrz odcinka łączącego
jest pewnym punktem wewnątrz odcinka łączącego ![]() z
z ![]() .
.
Dowód
Dowód wynika z zastosowania twierdzenia 1.10 do funkcji ![]() ,
, ![]() .
.
Definicja 2.2
Podzbiór ![]() jest wypukły, jeśli
jest wypukły, jeśli
dla każdych ![]() i każdego
i każdego ![]() .
.
Wniosek 2.1
Niech ![]() zbiór otwarty, wypukły oraz
zbiór otwarty, wypukły oraz ![]() klasy
klasy ![]() . Wówczas dla dowolnych
. Wówczas dla dowolnych ![]() mamy
mamy
gdzie ![]() należy do wnętrza odcinka łączącego
należy do wnętrza odcinka łączącego ![]() i
i ![]() , tzn. istnieje
, tzn. istnieje ![]() , taka że
, taka że ![]() .
.
Dowód
Z wypukłości ![]() wynika, że dla każdego
wynika, że dla każdego ![]() odcinek łączący te punkty zawarty jest w
odcinek łączący te punkty zawarty jest w ![]() . Teza wynika teraz z lematu 2.1.
. Teza wynika teraz z lematu 2.1.
2.2. Znikanie gradientu
Będziemy rozważać funkcję ![]() , gdzie
, gdzie ![]() jest podzbiorem w
jest podzbiorem w ![]() mającym niepuste wnętrze
mającym niepuste wnętrze ![]() .
.
Twierdzenie 2.2 (Warunek konieczny I rzędu)
Jeśli funkcja ![]() jest różniczkowalna w punkcie
jest różniczkowalna w punkcie ![]() należącym do wnętrza zbioru
należącym do wnętrza zbioru ![]() oraz
oraz ![]() jest lokalnym minimum (maksimum) funkcji
jest lokalnym minimum (maksimum) funkcji ![]() to
to
Dowód
Z faktu, że ![]() wynika, że funkcja
wynika, że funkcja ![]() , gdzie
, gdzie ![]() jest
jest ![]() -tym wersorem (tj.
-tym wersorem (tj. ![]() ma jedynkę na
ma jedynkę na ![]() -tej współrzędnej i zera poza nią), jest dobrze określona na otoczeniu
-tej współrzędnej i zera poza nią), jest dobrze określona na otoczeniu ![]() . Ma ona również lokalne ekstremum w punkcie
. Ma ona również lokalne ekstremum w punkcie ![]() . Na mocy tw. 1.4 mamy
. Na mocy tw. 1.4 mamy ![]() . W terminach funkcji
. W terminach funkcji ![]() oznacza to, że
oznacza to, że ![]() . Przeprowadzając to rozumowanie dla
. Przeprowadzając to rozumowanie dla ![]() dostajemy tezę..
dostajemy tezę..
Warunek znikania gradientu będzie często używany, zatem użyteczna będzie
Definicja 2.3
Punkt ![]() nazywamy punktem krytycznym funkcji
nazywamy punktem krytycznym funkcji ![]() , jeśli
, jeśli ![]() jest różniczkowalna w
jest różniczkowalna w ![]() oraz
oraz ![]() .
.
Oczywiście, warunek znikania gradientu ![]() nie jest wystarczający na to, by w
nie jest wystarczający na to, by w ![]() znajdowało się lokalne minimum lub maksimum. Do rozstrzygnięcia tego jest potrzebny analog warunku o znaku drugiej pochodnej (tw. 1.6). W przypadku wielowymiarowym ten warunek definiuje się jako dodatnią (ujemną) określoność macierzy drugich pochodnych.
znajdowało się lokalne minimum lub maksimum. Do rozstrzygnięcia tego jest potrzebny analog warunku o znaku drugiej pochodnej (tw. 1.6). W przypadku wielowymiarowym ten warunek definiuje się jako dodatnią (ujemną) określoność macierzy drugich pochodnych.
2.3. Dodatnia i ujemna określoność macierzy
Niech ![]() będzie macierzą symetryczną, tzn.
będzie macierzą symetryczną, tzn. ![]() . Rozważmy formę kwadratową
. Rozważmy formę kwadratową
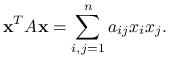 |
Definicja 2.4
Określoność macierzy ![]() lub formy kwadratowej
lub formy kwadratowej ![]() definiujemy następująco:
definiujemy następująco:
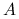 jest nieujemnie określona, co oznaczamy
jest nieujemnie określona, co oznaczamy 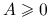 , jeśli
, jeśli
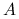 jest dodatnio określona, co oznaczamy
jest dodatnio określona, co oznaczamy 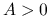 , jeśli
, jeśli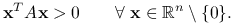
Odwracając nierówności definiujemy niedodatnią określoność i ujemną określoność.
Macierz
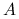 nazywamy nieokreśloną, jeśli istnieją wektory
nazywamy nieokreśloną, jeśli istnieją wektory 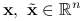 takie, że
takie, że

Zauważmy, że z definicji określoności macierzy, wyliczając wyrażenie ![]() na wersorze
na wersorze ![]() , z jedynką na
, z jedynką na ![]() -tym miejscu, wynikają następujące warunki konieczne odpowiedniej określoności macierzy
-tym miejscu, wynikają następujące warunki konieczne odpowiedniej określoności macierzy ![]() :
:
Jeśli
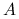 jest dodatnio określona, to
jest dodatnio określona, to
 .
.Jeśli
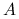 jest nieujemnie określona, to
jest nieujemnie określona, to
 .
.Jeśli
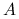 jest ujemnie określona, to
jest ujemnie określona, to
 .
.Jeśli
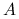 jest niedodatnio określona, to
jest niedodatnio określona, to
 .
.Jeśli
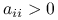 i
i 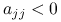 , dla pewnych
, dla pewnych 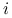 ,
, 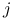 , to
, to
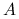 jest nieokreślona.
jest nieokreślona.
Warunki konieczne i dostateczne podane są w poniższym twierdzeniu, którego dowód pomijamy.
Twierdzenie 2.3 (Kryterium Sylvestera)
![]()
I. Forma kwadratowa
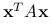 jest dodatnio określona wtedy i tylko wtedy, gdy zachodzi:
jest dodatnio określona wtedy i tylko wtedy, gdy zachodzi: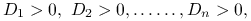
gdzie przez
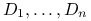 oznaczamy minory główne macierzy
oznaczamy minory główne macierzy 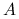 :
:![D_{1}=\det(a_{{11}}),\ D_{2}=\det\left(\begin{array}[]{cc}a_{{11}}&a_{{12}}\\
a_{{21}}&a_{{22}}\end{array}\right),\ldots,D_{n}=\det\left(\begin{array}[]{ccc}a_{{11}}&\ldots&a_{{1n}}\\
\vdots&\ddots&\vdots\\
a_{{n1}}&\ldots&a_{{nn}}\end{array}\right).](wyklady/op2/mi/mi283.png)
Forma kwadratowa
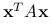 jest ujemnie określona wtedy i tylko wtedy, gdy
jest ujemnie określona wtedy i tylko wtedy, gdy 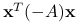 jest dodatnio określona, co przekłada się na ciąg warunków:
jest dodatnio określona, co przekłada się na ciąg warunków:
II. Forma kwadratowa
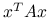 jest nieujemnie określona wtedy i tylko wtedy, gdy dla dowolnych
jest nieujemnie określona wtedy i tylko wtedy, gdy dla dowolnych 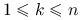 oraz
oraz 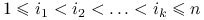 zachodzi
zachodzi![\det\left(\begin{array}[]{cccc}a_{{i_{1}i_{1}}}&a_{{i_{1}i_{2}}}&\ldots&a_{{i_{1}i_{k}}}\\
a_{{i_{2}i_{1}}}&a_{{i_{2}i_{2}}}&\ldots&a_{{i_{2}i_{k}}}\\
\vdots&\vdots&\ddots&\vdots\\
a_{{i_{k}i_{1}}}&a_{{i_{k}i_{2}}}&\ldots&a_{{i_{k}i_{k}}}\end{array}\right)\geq 0](wyklady/op2/mi/mi273.png)
(jest to minor rzędu
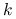 złożony z kolumn
złożony z kolumn  i rzędów
i rzędów  ).
).
Określoność macierzy symetrycznej jest niezależna od bazy, w której jest reprezentowana. W bazie własnej macierz ![]() jest diagonalna z wartościami własnymi na diagonali. Dostajemy zatem następujące warunki równoważne określoności:
jest diagonalna z wartościami własnymi na diagonali. Dostajemy zatem następujące warunki równoważne określoności:
Macierz
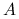 jest dodatnio określona wtw, gdy wszystkie jej wartości własne są dodatnie.
jest dodatnio określona wtw, gdy wszystkie jej wartości własne są dodatnie.Macierz
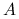 jest nieujemnie określona wtw, gdy wszystkie jej wartości własne są nieujemne.
jest nieujemnie określona wtw, gdy wszystkie jej wartości własne są nieujemne.Macierz
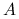 jest ujemnie określona wtw, gdy wszystkie jej wartości własne są ujemne.
jest ujemnie określona wtw, gdy wszystkie jej wartości własne są ujemne.Macierz
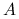 jest niedodatnio określona wtw, gdy wszystkie jej wartości własne są niedodatnie.
jest niedodatnio określona wtw, gdy wszystkie jej wartości własne są niedodatnie.
2.4. Warunki II-go rzędu (kryterium drugiej różniczki)
Twierdzenie 2.4 (Warunek konieczny II rzędu)
Jeśli ![]() jest klasy
jest klasy ![]() na zbiorze otwartym
na zbiorze otwartym ![]() i
i ![]() jest
minimum lokalnym, to macierz
jest
minimum lokalnym, to macierz ![]() jest nieujemnie określona. Podobnie, jeśli
jest nieujemnie określona. Podobnie, jeśli ![]() jest lokalnym maksimum, to
jest lokalnym maksimum, to ![]() jest
niedodatnio określona.
jest
niedodatnio określona.
Twierdzenie 2.5 (Warunek dostateczny II rzędu)
Jeśli ![]() jest klasy
jest klasy ![]() na zbiorze otwartym
na zbiorze otwartym ![]() ,
, ![]() oraz
oraz ![]() jest dodatnio określona
(ujemnie określona) to
jest dodatnio określona
(ujemnie określona) to ![]() ma ścisłe lokalne minimum (lokalne maksimum) w
ma ścisłe lokalne minimum (lokalne maksimum) w ![]() .
.
Dowód twierdzenia 2.4
Niech ![]() będzie minimum lokalnym
będzie minimum lokalnym ![]() . Ustalmy niezerowy wektor
. Ustalmy niezerowy wektor ![]() i funkcję
i funkcję
gdzie ![]() jest z dostatecznie małego otoczenia zera, aby
jest z dostatecznie małego otoczenia zera, aby ![]() . Wtedy funkcja
. Wtedy funkcja ![]() ma lokalne minimum w punkcie
ma lokalne minimum w punkcie ![]() . Ponieważ
. Ponieważ ![]() jest klasy
jest klasy ![]() , funkcja
, funkcja ![]() również jest klasy
również jest klasy ![]() . Z Twierdzenia 1.5 dla przypadku skalarnego wiemy, że skoro
. Z Twierdzenia 1.5 dla przypadku skalarnego wiemy, że skoro ![]() jest lokalnym minimum, to
jest lokalnym minimum, to ![]() . Ze wzorów na pochodną funkcji złożonej mamy
. Ze wzorów na pochodną funkcji złożonej mamy
Z dowolności wektora ![]() wynika nieujemna określoność macierzy
wynika nieujemna określoność macierzy ![]() .
.
Dowód twierdzenia 2.5
Załóżmy najpierw, że ![]() . Określmy funkcję
. Określmy funkcję ![]() wzorem
wzorem
Funkcja ta jest ciągła na mocy ciągłości hesjanu ![]() oraz ćwiczenia 2.2. Istnieje zatem kula
oraz ćwiczenia 2.2. Istnieje zatem kula ![]() , taka że
, taka że ![]() dla
dla ![]() .
.
Ustalmy dowolny ![]() . Na mocy wzoru Taylora, lemat 2.1, mamy
. Na mocy wzoru Taylora, lemat 2.1, mamy
dla pewnego punktu ![]() leżącego na odcinku łączącym
leżącego na odcinku łączącym ![]() i
i ![]() , a zatem i należącego do kuli
, a zatem i należącego do kuli ![]() . Pierwsza pochodna
. Pierwsza pochodna ![]() znika w punkcie
znika w punkcie ![]() , zaś
, zaś
Mamy zatem
gdyż funkcja ![]() jest dodatnia na kuli
jest dodatnia na kuli ![]() . Wnioskujemy więc, że
. Wnioskujemy więc, że ![]() jest ścisłym minimum lokalnym.
jest ścisłym minimum lokalnym.
Dowód przypadku ![]() jest analogiczny.
jest analogiczny.
2.4.1. Ekstrema globalne i określoność drugiej różniczki
Niech teraz ![]() będzie funkcją klasy
będzie funkcją klasy ![]() na zbiorze wypukłym
na zbiorze wypukłym ![]() , oraz klasy
, oraz klasy ![]() na
na ![]() .
.
Twierdzenie 2.6
Jeśli ![]() jest punktem krytycznym
jest punktem krytycznym ![]() , to:
, to:
I)
 jest globalnym minimum,
jest globalnym minimum,II)
 jest globalnym maksimum.
jest globalnym maksimum.
Jeśli dodatkowo ![]() w pierwszym stwierdzeniu (
w pierwszym stwierdzeniu (![]() w drugim stwierdzeniu), to
w drugim stwierdzeniu), to ![]() jest ścisłym globalnym minimum
(maksimum).
jest ścisłym globalnym minimum
(maksimum).
Dowód
Jeśli ![]() , to z wypukłości
, to z wypukłości ![]() cały odcinek łączący
cały odcinek łączący ![]() z
z ![]() (poza punktem
(poza punktem ![]() ) leży w
) leży w ![]() i możemy zastosować wzór Taylora, lemat 2.1, który daje
i możemy zastosować wzór Taylora, lemat 2.1, który daje
gdzie ![]() jest pewnym punktem z odcinka łączącego
jest pewnym punktem z odcinka łączącego ![]() z
z ![]() . Nierówność
. Nierówność ![]() (odpowiednio,
(odpowiednio, ![]() ) oznacza, że drugi człon w powyższym wzorze jest nieujemny (niedodatni), co pociąga obie implikacje w twierdzeniu.
) oznacza, że drugi człon w powyższym wzorze jest nieujemny (niedodatni), co pociąga obie implikacje w twierdzeniu.
W przypadku, gdy w (I) mamy dodatkowo ![]() , odwołamy się do używanej już funkcji
, odwołamy się do używanej już funkcji ![]() ,
, ![]() . Z wypukłości
. Z wypukłości ![]() wynika, że
wynika, że ![]() jest dobrze określona, tzn.
jest dobrze określona, tzn. ![]() dla
dla ![]() . Nasze założenia implikują, że
. Nasze założenia implikują, że ![]() ,
, ![]() oraz
oraz ![]() . Możemy skorzystać z tw. 1.11, które stwierdza, że
. Możemy skorzystać z tw. 1.11, które stwierdza, że ![]() ma ścisłe globalne minimum w
ma ścisłe globalne minimum w ![]() . Zatem
. Zatem ![]() , czyli
, czyli ![]() . Z dowolności
. Z dowolności ![]() wynika, iż
wynika, iż ![]() jest ścisłym minimum globalnym.
jest ścisłym minimum globalnym.
Przypadek ![]() w stwierdzeniu (II) dowodzimy analogicznie.
w stwierdzeniu (II) dowodzimy analogicznie.
2.5. Zadania
Ćwiczenie 2.1
Wykaż, że hesjan funkcji
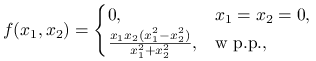 |
nie jest symetryczny w punkcie ![]() .
.
Ćwiczenie 2.2
Niech ![]() ,
, ![]() zwarty oraz
zwarty oraz ![]() ciągła. Udowodnij, że funkcja
ciągła. Udowodnij, że funkcja ![]() zadana wzorem
zadana wzorem
jest ciągła.
Ćwiczenie 2.3
Pochodną kierunkową funkcji ![]() w punkcie
w punkcie ![]() i kierunku
i kierunku ![]() nazywamy granicę
nazywamy granicę
Udowodnij, że ![]() jest przyjmowane dla
jest przyjmowane dla ![]() .
.
Ćwiczenie 2.4
Rozważmy następującą funkcję (czasami zwaną funkcją Peano):
Udowodnij, że funkcja
 ograniczona do każdej prostej przechodzącej przez
ograniczona do każdej prostej przechodzącej przez 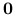 ma w tym punkcie minimum lokalne.
ma w tym punkcie minimum lokalne.Wykaż, że
 jako funkcja wielu zmiennych nie ma ekstremum lokalnego w
jako funkcja wielu zmiennych nie ma ekstremum lokalnego w 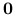 .
.Znajdź wartości własne macierzy drugiej pochodnej
 . Co możesz z nich wywnioskować? Czy tłumaczą one zachowanie funkcji
. Co możesz z nich wywnioskować? Czy tłumaczą one zachowanie funkcji  w
w 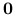 ?
?
Ćwiczenie 2.5
Rozważmy funkcję kwadratową wielu zmiennych:
gdzie ![]() jest macierzą kwadratową, niekoniecznie symetryczną,
jest macierzą kwadratową, niekoniecznie symetryczną, ![]() jest wektorem, zaś
jest wektorem, zaś ![]() stałą. Wyznacz gradient i hesjan (macierz drugiej pochodnej) funkcji
stałą. Wyznacz gradient i hesjan (macierz drugiej pochodnej) funkcji ![]() .
.
Załóż najpierw, że ![]() jest symetryczna. Udowodnij później, że dla każdej macierzy kwadratowej
jest symetryczna. Udowodnij później, że dla każdej macierzy kwadratowej ![]() istnieje macierz symetryczna
istnieje macierz symetryczna ![]() , taka że
, taka że ![]() dla każdego
dla każdego ![]() .
.
Ćwiczenie 2.6
Zbadaj określoność następujących macierzy i porównaj wyniki z ich formą zdiagonalizowaną:
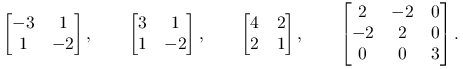 |
Ćwiczenie 2.7
Znajdź ekstrema globalne funkcji
Ćwiczenie 2.8
Niech ![]() będzie przestrzenią probabilistyczną, co między innymi oznacza, że
będzie przestrzenią probabilistyczną, co między innymi oznacza, że ![]() . Dana jest zmienna losowa
. Dana jest zmienna losowa ![]() , tzn. funkcja mierzalna
, tzn. funkcja mierzalna ![]() o tej własności, że
o tej własności, że ![]() . Znajdź wektor
. Znajdź wektor ![]() , taki że
, taki że ![]() jest najmniejsza.
jest najmniejsza.
Zapisz ![]() jako funkcję kwadratową.
jako funkcję kwadratową.
Ćwiczenie 2.9
Niech ![]() i
i ![]() . Załóżmy, że
. Załóżmy, że ![]() jest klasy
jest klasy ![]() na otoczeniu
na otoczeniu ![]() oraz
oraz ![]() . Udowodnij, że jeśli macierz
. Udowodnij, że jeśli macierz ![]() jest nieokreślona, to
jest nieokreślona, to ![]() nie ma ekstremum lokalnego w
nie ma ekstremum lokalnego w ![]() .
.
Ćwiczenie 2.10
Udowodnij nierówność średnich rozwiązując zadanie optymalizacyjne:
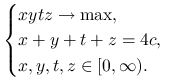 |
Ćwiczenie 2.11
Znajdź minima lokalne funkcji




