Zagadnienia

3.1 Zbiory wypukłe i twierdzenia o oddzielaniu
3.2 Definicja funkcji wypukłej
3.3 Własności funkcji wypukłych
3.4 Charakteryzacje funkcji wypukłej
3.5 Subróżniczka
3.6 Zadania

3. Funkcje wypukłe

3.1. Zbiory wypukłe i twierdzenia o oddzielaniu

Przypomnijmy, za def. 2.2, definicję zbioru wypukłego: zbiór $W\subset\mathbb{R}^{n}$ jest wypukły, jeśli

$\lambda\mathbf{x}+(1-\lambda)\mathbf{y}\in W$

dla każdych $\mathbf{x},\mathbf{y}\in W$ i każdego $\lambda\in[0,1]$ . Równoważnie można wypukłość zdefiniować za pomocą $m$ -tek punktów:

Lemat 3.1

Zbiór $W\subset\mathbb{R}^{n}$ jest wypukły wtw, gdy dla dowolnego $m\ge 2$ , punktów $\mathbf{x}_{1},\ldots,\mathbf{x}_{m}\in W$ oraz liczb $a_{1},\ldots,a_{m}\ge 0$ , takich że $a_{1}+\ldots+a_{m}=1$ mamy

$a_{1}\mathbf{x}_{1}+a_{2}\mathbf{x}_{2}+\ldots+a_{m}\mathbf{x}_{m}\in W.$

Dowód tego lematu pozostawiamy jako ćwiczenie (patrz ćw. 3.3). Udowodnimy natomiast geometryczną własność zbiorów wypukłych, która przyda nam się wielokrotnie.

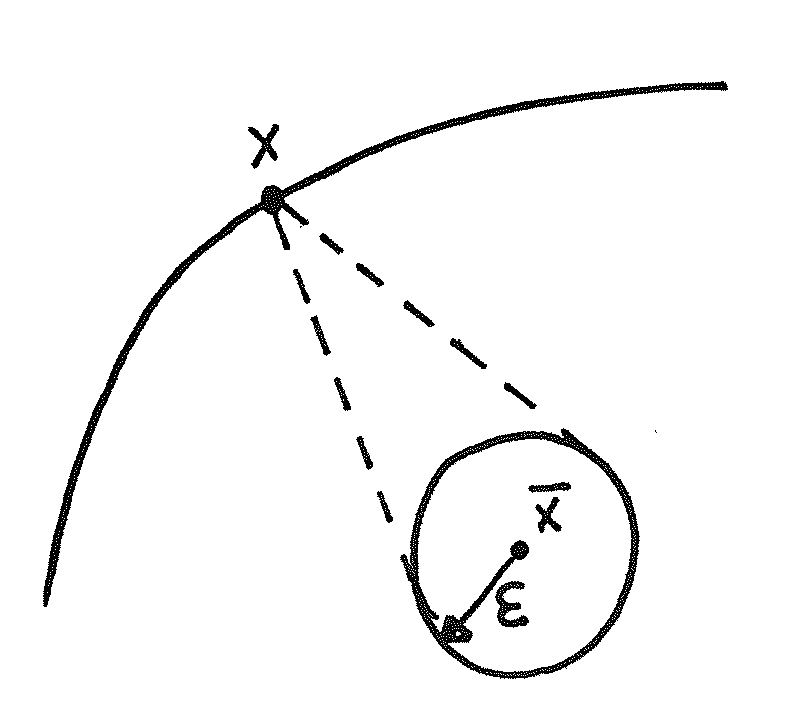
Lemat 3.2

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym o niepustym wnętrzu. Wówczas:

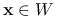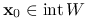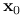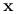I) Dla dowolnego $\mathbf{x}\in W$ oraz $\mathbf{x}_{0}\in\mathop{\rm int}W$ odcinek łączący $\mathbf{x}_{0}$ z $\mathbf{x}$ , z pominięciem punktu 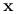$\mathbf{x}$ , należy do wnętrza $W$ :

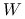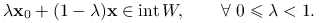
$\lambda\mathbf{x}_{0}+(1-\lambda)\mathbf{x}\in\mathop{\rm int}W,\qquad\forall\ 0\le\lambda<1.$
II) $W\subset\mathop{\rm cl}(\mathop{\rm int}W)$ .

Dowód

Weźmy punkty $\mathbf{x}_{0}$ i $\mathbf{x}$ jak w założeniach lematu. Z otwartości $\mathop{\rm int}W$ wynika, że istnieje kula $B(\mathbf{x}_{0},\varepsilon)\subset\mathop{\rm int}W$ . Połączmy punkty tej kuli z punktem $\mathbf{x}$ . Dostaniemy ,,stożek” o wierzchołku $\mathbf{x}$ i podstawie $B(\mathbf{x}_{0},\varepsilon)$ (patrz rys. 3.1). Stożek ten leży w całości w $W$ . Jego wnętrze zawiera odcinek od $\mathbf{x}_{0}$ do $\mathbf{x}$ bez końca $\mathbf{x}$ . Kończy to zatem dowód (I). Dowód (II) wynika natychmiast z (I).

Rys. 3.1. Stożek o wierzchołku $\mathbf{x}$ i podstawie $B({\bar{\mathbf{x}}},\varepsilon)$ .

∎

Przypomnijmy bez dowodu twierdzenia o oddzielaniu zbiorów wypukłych w przestrzeniach $\mathbb{R}^{n}$ (dowody tych twierdzeń można znaleźć np. w rozdziale 2.4 monografii Bazaraa, Sherali, Shetty [3] lub w rozdziale 11 monografii Rockafellar'a [11]).

Twierdzenie 3.1 (Słabe twierdzenie o oddzielaniu)

Niech $U,V\subset\mathbb{R}^{n}$ będą niespustymi zbiorami wypukłymi, takimi że $U\cap V=\emptyset$ . Wówczas istnieje hiperpłaszczyzna rozdzielająca $U$ od $V$ , tzn. istnieje niezerowy wektor $\mathbf{a}\in\mathbb{R}^{n}$ spełniający

$\mathbf{a}^{T}\mathbf{x}\le\mathbf{a}^{T}\mathbf{y},\qquad\mathbf{x}\in U,\ \mathbf{y}\in V.$

Korzystając z ciągłości odwzorowania liniowego $\mathbf{x}\mapsto\mathbf{a}^{T}\mathbf{x}$ dostajemy bardzo przydatny wniosek, który również będziemy nazywać słabym twierdzeniem o oddzielaniu.

Wniosek 3.1

Niech $U,V\subset\mathbb{R}^{n}$ będą niepustymi zbiorami wypukłymi, takimi że $\mathop{\rm int}U\ne\emptyset$ i $(\mathop{\rm int}U)\cap V=\emptyset$ . Wówczas istnieje hiperpłaszczyzna rozdzielająca $U$ od $V$ , tzn. istnieje niezerowy wektor $\mathbf{a}\in\mathbb{R}^{n}$ spełniający

$\mathbf{a}^{T}\mathbf{x}\le\mathbf{a}^{T}\mathbf{y},\qquad\mathbf{x}\in U,\ \mathbf{y}\in V.$

Twierdzenie 3.2 (Mocne twierdzenie o oddzielaniu)

Niech $U,V\subset\mathbb{R}^{n}$ będą niepustymi zbiorami wypukłymi domkniętymi, $U$ zwarty i $U\cap V=\emptyset$ . Wówczas istnieje hiperpłaszczyzna ściśle rozdzielająca $U$ od $V$ , tzn. istnieje niezerowy wektor $\mathbf{a}\in\mathbb{R}^{n}$ spełniający

$\sup _{{\mathbf{x}\in U}}\mathbf{a}^{T}\mathbf{x}<\inf _{{\mathbf{y}\in V}}\mathbf{a}^{T}\mathbf{y}.$

Uwaga 3.1

Powyższe twierdzenia mają intuicyjną geometryczną interpretację. Dwa rozłączne zbiory wypukłe mogą być rozdzielone hiperpłaszczyzną w ten sposób, iż jeden z nich leży w domkniętej półprzestrzeni po jednej stronie hiperpłaszczyzny, podczas gdy drugi leży po przeciwnej stronie tejże hiperpłaszczyzny. W słabym twierdzeniu nie możemy zagwarantować, iż któryś ze zbiorów leży we wnętrzu półprzestrzeni, tzn. ma puste przecięcie z hiperpłaszczyzną. Silna wersja właśnie to gwarantuje.

Hiperpłaszczyzna, o której mowa w twierdzeniach zadana jest wzorem:

$\{\mathbf{x}\in\mathbb{R}^{n}:\mathbf{a}^{T}\mathbf{x}=\alpha\},$

gdzie $\alpha=\sup _{{\mathbf{x}\in U}}\mathbf{a}^{T}\mathbf{x}$ . Nie musi to być jedyna hiperpłaszczyzna spełniająca warunki słabego/mocnego rozdzielania.

Twierdzenia o oddzielaniu będziemy dowodzić w przeciwnej kolejności niż są podane. Okazuje się bowiem, że łatwiej udowodnić twierdzenie mocne. Później w dowodzie twierdzenia słabego skorzystamy z mocnego oddzielania zbiorów wypukłych.

Dowód twierdzenia 3.2

Określmy funkcję $d:U\times V\to\mathbb{R}$ wzorem $d(\mathbf{x},\mathbf{y})=\|\mathbf{x}-\mathbf{y}\|$ . Z ograniczoności zbioru $U$ wynika, że $d$ jest funkcją koercywną; zbieżność do nieskończoności może się tylko odbywać po argumencie ze zbioru $V$ . Na mocy tw. 1.2 funkcja $d$ jako ciągła i koercywna określona na zbiorze domkniętym $U\times V$ osiąga swoje minimum w pewnym punkcie $(\mathbf{x}_{0},\mathbf{y}_{0})\in U\times V$ . Z faktu, że $U\cap V=\emptyset$ wynika, że $\mathbf{x}_{0}\ne\mathbf{y}_{0}$ . Połóżmy $\mathbf{a}=\mathbf{y}_{0}-\mathbf{x}_{0}$ . Pokażemy, że jest to szukany wektor z tezy twierdzenia.

Udowodnimy, że $\mathbf{a}^{T}\mathbf{y}\ge\mathbf{a}^{T}\mathbf{y}_{0}$ . Niech $\mathbf{y}\in V$ , $\mathbf{y}\ne\mathbf{y}_{0}$ . Zdefiniujmy funkcję

$g(t)=\Big(d\big(\mathbf{x}_{0},\mathbf{y}_{0}+t(\mathbf{y}-\mathbf{y}_{0})\big)\Big)^{2},\qquad t\in\mathbb{R}.$

Rozwijając dostajemy

$g(t)=\|\mathbf{y}_{0}-\mathbf{x}_{0}\|^{2}+2t(\mathbf{y}_{0}-\mathbf{x}_{0})^{T}(\mathbf{y}-\mathbf{y}_{0})+t^{2}(\mathbf{y}-\mathbf{y}_{0})^{T}(\mathbf{y}-\mathbf{y}_{0}).$

Funkcja ta jest różniczkowalna dla $t\in\mathbb{R}$ i $g(0)\le g(t)$ dla $t\in[0,1]$ (na mocy wypukłości $V$ i definicji $\mathbf{y}_{0}$ ). Zatem $g^{{\prime}}(0)\ge 0$ , czyli

$(\mathbf{y}_{0}-\mathbf{x}_{0})^{T}(\mathbf{y}-\mathbf{y}_{0})\ge 0.$

Nierówność ta jest równoważna $\mathbf{a}^{T}\mathbf{y}\ge\mathbf{a}^{T}\mathbf{y}_{0}$ .

Podobnie pokazujemy, że $\mathbf{a}^{T}\mathbf{x}\le\mathbf{a}^{T}\mathbf{x}_{0}$ dla $\mathbf{x}\in U$ . Do zakończenia dowodu wystarczy sprawdzić, że $\mathbf{a}^{T}\mathbf{y}_{0}>\mathbf{a}^{T}\mathbf{x}_{0}$ . Ta nierówność jest równoważna $\|\mathbf{a}\|^{2}>0$ , co zachodzi, gdyż $\mathbf{x}_{0}\ne\mathbf{y}_{0}$ .

∎

Dowód twierdzenia 3.1

Rozważmy zbiór $C=V-U=\{\mathbf{y}-\mathbf{x}:\ \mathbf{x}\in U,\ \mathbf{y}\in V\}$ . Zbiór ten jest wypukły i $\mathbf{0}\notin C$ . Równoważne tezie twierdzenia jest znalezienie wektora niezerowego $\mathbf{a}\in\mathbb{R}^{n}$ oddzielającego $C$ od $\{\mathbf{0}\}$ , tzn. takiego że $\mathbf{a}^{T}\mathbf{x}\ge 0$ dla $\mathbf{x}\in C$ .

Zdefiniujmy zbiory

$A_{\mathbf{x}}=\{\mathbf{a}\in\mathbb{R}^{n}:\ \|\mathbf{a}\|=1,\ \mathbf{a}^{T}\mathbf{x}\ge 0\}.$

Wystarczy pokazać, że $\bigcap _{{\mathbf{x}\in C}}A_{\mathbf{x}}\ne\emptyset$ . Będziemy rozumować przez sprzeczność. Załóżmy więc, że $\bigcap _{{\mathbf{x}\in C}}A_{\mathbf{x}}=\emptyset$ . Niech $B_{\mathbf{x}}=S\setminus A_{\mathbf{x}}$ , gdzie $S$ jest sferą jednostkową $S=\{\mathbf{a}\in\mathbb{R}^{n}:\ \|\mathbf{a}\|=1\}$ . Zbiory $B_{\mathbf{x}}$ , $\mathbf{x}\in C$ , są otwartymi podzbiorami zbioru zwartego $S$ . Z założenia, że przecięcie ich dopełnień w $S$ jest puste, wynika, że rodzina $\{ B_{\mathbf{x}}\} _{{\mathbf{x}\in C}}$ jest pokryciem otwartym $S$ . Na mocy zwartości $S$ istnieje podpokrycie skończone $B_{{\mathbf{x}_{1}}},\ldots,B_{{\mathbf{x}_{k}}}$ , czyli

$A_{{\mathbf{x}_{1}}}\cap\cdots\cap A_{{\mathbf{x}_{k}}}=\emptyset.$

Połóżmy

$\hat{C}=\mathop{\rm conv}\{\mathbf{x}_{1},\ldots,\mathbf{x}_{k}\}=\{\sum _{{i=1}}^{k}\lambda _{i}\mathbf{x}_{i}:\ \lambda _{1},\ldots,\lambda _{k}\ge 0,\ \sum _{{i=1}}^{k}\lambda _{i}=1\}.$

Zbiór $\hat{C}$ jest wypukły i domknięty oraz $\hat{C}\subset C$ . Stąd $\mathbf{0}\notin\hat{C}$ i na mocy mocnego twierdzenia o oddzielaniu zastosowanego do $\hat{C}$ i $\{\mathbf{0}\}$ istnieje wektor $\mathbf{a}\in\mathbb{R}^{n}\setminus\{\mathbf{0}\}$ , taki że

$\mathbf{a}^{T}\mathbf{x}>0,\qquad\mathbf{x}\in\hat{C}.$

W szczególności, $\mathbf{a}^{T}\mathbf{x}_{1}>0,\ldots,\mathbf{a}^{T}\mathbf{x}_{k}>0$ , czyli $\frac{\mathbf{a}}{\|\mathbf{a}\|}\in A_{{\mathbf{x}_{i}}}$ , $i=1,\ldots,k$ , co przeczy założeniu, że przecięcie $\bigcap _{{i=1}}^{k}A_{{\mathbf{x}_{i}}}=\emptyset$ .

∎

3.2. Definicja funkcji wypukłej

Definicja 3.1

Funkcję $f:W\to\mathbb{R}$ , gdzie $W\subset\mathbb{R}^{n}$ wypukły, nazwiemy:

wypukłą, jeśli dla każdego $\mathbf{x},\mathbf{y}\in W$ i $\lambda\in(0,1)$ zachodzi

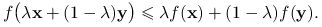
$f\big(\lambda\mathbf{x}+(1-\lambda)\mathbf{y}\big)\le\lambda f(\mathbf{x})+(1-\lambda)f(\mathbf{y}).$
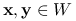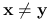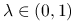ściśle wypukłą, jeśli dla każdego $\mathbf{x},\mathbf{y}\in W$ , $\mathbf{x}\ne\mathbf{y}$ i $\lambda\in(0,1)$ zachodzi

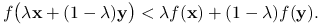
$f\big(\lambda\mathbf{x}+(1-\lambda)\mathbf{y}\big)<\lambda f(\mathbf{x})+(1-\lambda)f(\mathbf{y}).$

Funkcja $f$ jest (ściśle) wklęsła, jeśli $(-f)$ jest (ściśle) wypukła.

Okazuje się, że wystarczy rozważać $\lambda=1/2$ w definicji wypukłości. Zacytujemy najpierw silny wynik noszący nazwisko Sierpińskiego, a później łatwiejszy, który dowiedziemy:

Twierdzenie 3.3

Jeśli funkcja $f:W\to\mathbb{R}$ , gdzie $W\subset\mathbb{R}^{n}$ wypukły, jest mierzalna w sensie Lebesgue'a oraz spełnia

$f\Big(\frac{\mathbf{x}+\mathbf{y}}{2}\Big)\le\frac{f(\mathbf{x})+f(\mathbf{y})}{2},$

to jest wypukła.

Dowód

Patrz dowód tw. Sierpińskiego w [7, str. 12].

∎

My udowodnimy słabszy wynik; założymy mianowicie ciągłość $f$ .

Twierdzenie 3.4

Jeśli funkcja $f:W\to\mathbb{R}$ , gdzie $W\subset\mathbb{R}^{n}$ wypukły, jest ciągła oraz spełnia

$f\Big(\frac{\mathbf{x}+\mathbf{y}}{2}\Big)\le\frac{f(\mathbf{x})+f(\mathbf{y})}{2},$

to jest wypukła.

Dowód

Pokażemy najpierw, przez indukcję po $k$ , że nierówność wypukłości zachodzi dla $\lambda$ postaci $p/2^{k}$ , $p=0,1,\ldots,2^{k}$ . Własność ta jest spełniona dla $k=1$ z założenia twierdzenia. Przeprowadźmy teraz krok indukcyjny. Załóżmy, że nierówność jest prawdziwa dla $k$ . Weźmy $p,q>0$ całkowite, o sumie $p+q=2^{{k+1}}$ . Załóżmy $p\le q$ . Wówczas $p\le 2^{k}\le q$ i możemy napisać:

$\mathbf{z}=\frac{p}{2^{{k+1}}}\mathbf{x}+\frac{q}{2^{{k+1}}}\mathbf{y}=\frac{1}{2}\bigg(\frac{p}{2^{k}}\mathbf{x}+\frac{q-2^{k}}{2^{k}}\mathbf{y}+\mathbf{y}\bigg).$

Mamy zatem

$f(\mathbf{z})\le\frac{1}{2}f\Big(\frac{p}{2^{k}}\mathbf{x}+\frac{q-2^{k}}{2^{k}}\mathbf{y}\Big)+\frac{1}{2}f(\mathbf{y})\le\frac{1}{2}\frac{p}{2^{k}}f(\mathbf{x})+\frac{1}{2}\frac{q-2^{k}}{2^{k}}f(\mathbf{y})+\frac{1}{2}f(\mathbf{y})=\frac{p}{2^{{k+1}}}f(\mathbf{x})+\frac{q}{2^{{k+1}}}f(\mathbf{y}).$

Pierwsza nierówność wynika z założenia twierdzenia, zaś druga – z założenia indukcyjnego. Dowód w przypadku $p\ge q$ jest symetryczny, ze zmienioną rolą $\mathbf{x}$ i $\mathbf{y}$ .

Zbiór punktów postaci $p/2^{k}$ , $k=1,2,\ldots$ , jest gęsty w odcinku $(0,1)$ . Z ciągłości funkcji $f$ otrzymujemy nierówność wypukłości dla dowolnego $\lambda\in(0,1)$ .

∎

Przykład 3.1

Funkcja afiniczna 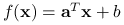$f(\mathbf{x})=\mathbf{a}^{T}\mathbf{x}+b$ jest wypukła i wklęsła.
Norma w 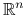$\mathbb{R}^{n}$ jest funkcją wypukłą. Wystarczy skorzystać z nierówności trójkąta.
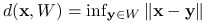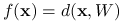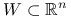Odległość punktu od zbioru definiujmy następująco $d(\mathbf{x},W)=\inf _{{\mathbf{y}\in W}}\|\mathbf{x}-\mathbf{y}\|$ . Odległość punktu od zbioru wypukłego jest funkcją wypukłą: $f(\mathbf{x})=d(\mathbf{x},W)$ dla pewnego zbioru wypukłego $W\subset\mathbb{R}^{n}$ .

3.3. Własności funkcji wypukłych

W tym rozdziale zakładamy, iż funkcja $f:W\to R$ jest określona na niepustym wypukłym podzbiorze $W\subset\mathbb{R}^{n}$ .

Definicja 3.2

Epigrafem funkcji $f:W\to\mathbb{R}$ nazywamy zbiór

$\mathop{\rm epi}(f)=\big\{(\mathbf{x},z)\in W\times\mathbb{R}:z\ge f(\mathbf{x})\big\}.$

Definicja 3.3

Zbiorem poziomicowym funkcji $f:W\to\mathbb{R}$ nazywamy

$W_{\alpha}(f)=\big\{\mathbf{x}\in W:f(\mathbf{x})\le\alpha\big\},\qquad\alpha\in\mathbb{R}.$

Twierdzenie 3.5 (Twierdzenie o epigrafie)

Funkcja $f$ jest wypukła wtedy i tylko wtedy, gdy jej epigraf $\mathop{\rm epi}(f)$ jest wypukłym podzbiorem $\mathbb{R}^{{n+1}}$ .

Twierdzenie 3.6

Jeśli funkcja $f$ jest wypukła, to zbiór poziomicowy $W_{\alpha}(f)$ jest wypukły dla dowolnego $\alpha$ .

Dowód powyższych twierdzeń pozostawiamy czytelnikowi.

Uwaga 3.2

Twierdzenie odwrotne do tw. 3.6 nie jest prawdziwe. Połóżmy $W=\mathbb{R}^{n}$ i weźmy dowolny niepusty wypukły zbiór $A\subset\mathbb{R}^{n}$ . Rozważmy funkcję

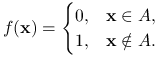$f(\mathbf{x})=\begin{cases}0,&\mathbf{x}\in A,\\ 1,&\mathbf{x}\notin A.\end{cases}$

Każdy zbiór poziomicowy tej funkcji jest wypukły, zaś funkcja nie jest wypukła.

Okazuje się, że wypukłość gwarantuje ciągłość we wnętrzu $\mathop{\rm int}W$ . Rezultat ten nie może być rozszerzony na brzeg $W$ .

Twierdzenie 3.7

Jeśli funkcja $f$ jest wypukła, to jest również ciągła na $\mathop{\rm int}W$ .

Dowód powyższego twierdzenia wykracza poza ramy tego wykładu. Zainteresowany czytelnik może go znaleźć w monografii [10] w rozdziale IV.41.

Twierdzenie 3.8 (Twierdzenie o hiperpłaszczyźnie podpierającej)

Jeśli $f$ jest wypukła, to w każdym punkcie $\bar{\mathbf{x}}\in\mathop{\rm int}W$ istnieje hiperpłaszczyzna podpierająca, tzn. istnieje $\xi\in\mathbb{R}^{n}$ takie że

$f(\mathbf{x})\ge f(\bar{\mathbf{x}})+\xi^{T}(\mathbf{x}-\bar{\mathbf{x}}),\qquad\forall\,\mathbf{x}\in W.$

Jeśli $f$ jest ściśle wypukła, to

$f(\mathbf{x})>f(\bar{\mathbf{x}})+\xi^{T}(\mathbf{x}-\bar{\mathbf{x}}),\qquad\forall\,\mathbf{x}\in W\setminus\{{\bar{\mathbf{x}}}\}.$

Jeśli $f$ jest różniczkowalna w ${\bar{\mathbf{x}}}$ , to w obu powyższych nierównościach możemy przyjąć $\xi=Df({\bar{\mathbf{x}}})^{T}$ .

Dowód tw. 3.8

Na mocy twierdzenia 3.5, epigraf $\mathop{\rm epi}(f)$ jest zbiorem wypukłym. Zastosujemy słabe twierdzenie o oddzielaniu do zbiorów $U=\mathop{\rm epi}(f)$ i $V=\{({\bar{\mathbf{x}}},f({\bar{\mathbf{x}}}))\}$ . Istnieje niezerowy wektor $\mathbf{a}=(\xi,\alpha)\in\mathbb{R}^{n}\times\mathbb{R}$ , takie że

$\xi^{T}\mathbf{x}+\alpha y\le\xi^{T}{\bar{\mathbf{x}}}+\alpha f({\bar{\mathbf{x}}})$

(3.1)

dla $(\mathbf{x},y)\in\mathop{\rm epi}(f)$ . Nierówność ta musi być prawdziwa dla wszystkich $y\ge f(\mathbf{x})$ . Zatem $\alpha\le 0$ . Okazuje się, że $\alpha\ne 0$ . Dowiedziemy tego przez sprzeczność: załóżmy $\alpha=0$ . Wówczas dla dowolnego $\mathbf{x}\in W$ mamy $\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}})\le 0$ . Korzystając z tego, że ${\bar{\mathbf{x}}}$ jest we wnętrzu $W$ , wiemy, że ${\bar{\mathbf{x}}}+\varepsilon\xi\in W$ dla dostatecznie małego $\varepsilon>0$ . Połóżmy $\mathbf{x}={\bar{\mathbf{x}}}+\varepsilon\xi$ . Wtedy $0\ge\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}})=\varepsilon\xi^{T}\xi=\varepsilon\|\xi\|^{2}$ , a zatem $\xi=\mathbf{0}$ . Przeczy to niezerowości wektora $(\xi,\alpha)$ . Wnioskujemy więc, że $\alpha<0$ .

Możemy założyć, że $\alpha=-1$ w nierówności (3.1) (wystarczy podzielić obie strony przez $|\alpha|$ ). Dla dowolnego $\mathbf{x}\in W$ dostajemy zatem

$\xi^{T}\mathbf{x}-f(\mathbf{x})\le\xi^{T}{\bar{\mathbf{x}}}-f({\bar{\mathbf{x}}}),$

co przepisujemy następująco

$f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}}).$

Kończy to dowód pierwszej części twierdzenia.

Załóżmy teraz, że $f$ jest różniczkowalna w ${\bar{\mathbf{x}}}$ . Dla dowolnego $\mathbf{x}\in W$ , $\mathbf{x}\ne{\bar{\mathbf{x}}}$ i $\lambda\in(0,1)$ , z wypukłości mamy

$\displaystyle f(\mathbf{x})-f({\bar{\mathbf{x}}})$	$\displaystyle=\frac{(1-\lambda)f({\bar{\mathbf{x}}})+\lambda f(\mathbf{x})-f({\bar{\mathbf{x}}})}{\lambda}$
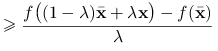	$\displaystyle\ge\frac{f\big((1-\lambda){\bar{\mathbf{x}}}+\lambda\mathbf{x}\big)-f({\bar{\mathbf{x}}})}{\lambda}$	(3.2)
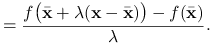	$\displaystyle=\frac{f\big({\bar{\mathbf{x}}}+\lambda(\mathbf{x}-{\bar{\mathbf{x}}})\big)-f({\bar{\mathbf{x}}})}{\lambda}.$

Policzmy granicę, gdy $\lambda$ dąży do zera:

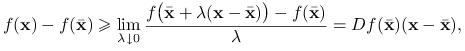$f(\mathbf{x})-f({\bar{\mathbf{x}}})\ge\lim _{{\lambda\downarrow 0}}\frac{f\big({\bar{\mathbf{x}}}+\lambda(\mathbf{x}-{\bar{\mathbf{x}}})\big)-f({\bar{\mathbf{x}}})}{\lambda}=Df({\bar{\mathbf{x}}})(\mathbf{x}-{\bar{\mathbf{x}}}),$

gdzie istnieje granicy i ostatnia równość wynika z różniczkowalności $f$ w punkcie ${\bar{\mathbf{x}}}$ .

Przypuśćmy, że $f$ jest ściśle wypukła. Ustalmy ${\bar{\mathbf{x}}}\in\mathop{\rm int}W$ . Na mocy pierwszej części twierdzenia $f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}})$ dla dowolnego $\mathbf{x}\in W$ . Przypuśćmy, że dla pewnego $\mathbf{x}\in W$ , $\mathbf{x}\ne{\bar{\mathbf{x}}}$ , ta nierówność nie jest ścisła, tj. $f(\mathbf{x})=f({\bar{\mathbf{x}}})+\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}})$ . Ze ścisłej wypukłości dostajemy

$f\Big(\frac{{\bar{\mathbf{x}}}+\mathbf{x}}{2}\Big)<\frac{1}{2}f(\mathbf{x})+\frac{1}{2}f({\bar{\mathbf{x}}})=f({\bar{\mathbf{x}}})+\frac{1}{2}\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}}).$

(3.3)

Z drugiej strony, z istnienia płaszczyzny podpierającej w ${\bar{\mathbf{x}}}$ mamy

$f\Big(\frac{{\bar{\mathbf{x}}}+\mathbf{x}}{2}\Big)\ge f({\bar{\mathbf{x}}})+\xi^{T}\Big(\frac{\mathbf{x}+{\bar{\mathbf{x}}}}{2}-{\bar{\mathbf{x}}}\Big)=f({\bar{\mathbf{x}}})+\xi^{T}\frac{\mathbf{x}-{\bar{\mathbf{x}}}}{2}.$

Dostajemy sprzeczność z nierównością (3.3). Pokazuje to, że dla funkcji ściśle wypukłej $f$ musi być spełniona ścisła nierówność $f(\mathbf{x})<f({\bar{\mathbf{x}}})+\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}})$ jeśli tylko $\mathbf{x}\ne{\bar{\mathbf{x}}}$ .

∎

Prawdziwe jest twierdzenie odwrotne do twierdzenia 3.8 (patrz tw. 3.9).

Wniosek 3.2

Jeśli $f$ wypukła i różniczkowalna w ${\bar{\mathbf{x}}}\in\mathop{\rm int}W$ , to w ${\bar{\mathbf{x}}}$ jest minimum globalne wtw, gdy $Df({\bar{\mathbf{x}}})=0$ .

Dowód

Implikacja w prawą stronę wynika z tw. 1.4. Aby dowieść implikacji przeciwnej, załóżmy $Df({\bar{\mathbf{x}}})=0$ dla pewnego ${\bar{\mathbf{x}}}=0$ . Na mocy tw. 3.8 dla dowolnego $\mathbf{x}\in W$ mamy

$f(\mathbf{x})\ge f(\bar{\mathbf{x}})+Df({\bar{\mathbf{x}}})(\mathbf{x}-\bar{\mathbf{x}})=f({\bar{\mathbf{x}}}),$

co dowodzi, że w punkcie ${\bar{\mathbf{x}}}$ jest minimum globalne.

∎

Poniżej wymieniamy pozostałe własności funkcji wypukłych. Ich dowody pozostawione są jako ćwiczenia.

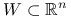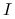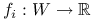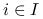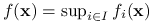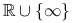Niech $W\subset\mathbb{R}^{n}$ , wypukły, zaś $I$ dowolny zbiór. Jeśli funkcje $f_{i}:W\to\mathbb{R}$ , $i\in I$ , są wypukłe, to $f(\mathbf{x})=\sup _{{i\in I}}f_{i}(\mathbf{x})$ jest wypukła ze zbiorem wartości $\mathbb{R}\cup\{\infty\}$ .
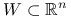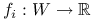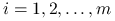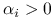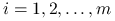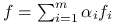Niech $W\subset\mathbb{R}^{n}$ , wypukły. Jeśli funkcje $f_{i}:W\to\mathbb{R}$ , $i=1,2,\ldots,m$ , są wypukłe i $\alpha _{i}>0$ dla $i=1,2,\ldots,m$ , to funkcja $f=\sum _{{i=1}}^{m}\alpha _{i}f_{i}$ jest wypukła. Jeśli jedna z funkcji 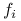$f_{i}$ jest ściśle wypukła, to $f$ jest również ściśle wypukła.
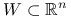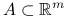Niech $W\subset\mathbb{R}^{n}$ , $A\subset\mathbb{R}^{m}$ wypukłe zbiory. Jeśli funkcja 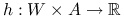$h:W\times A\to\mathbb{R}$ jest wypukła i ograniczona z dołu, to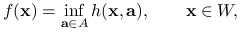

$f(\mathbf{x})=\inf _{{\mathbf{a}\in A}}h(\mathbf{x},\mathbf{a}),\qquad\mathbf{x}\in W,$

jest wypukła.
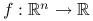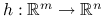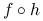Niech $f:\mathbb{R}^{n}\to\mathbb{R}$ wypukła. Jeśli $h:\mathbb{R}^{m}\to\mathbb{R}^{n}$ afiniczna, to złożenie $f\circ h$ jest funkcją wypukłą.
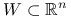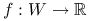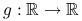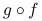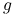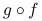Niech $W\subset\mathbb{R}^{n}$ wypukły. Jeśli $f:W\to\mathbb{R}$ jest funkcją wypukłą i $g:\mathbb{R}\to\mathbb{R}$ jest wypukła i niemalejąca, to $g\circ f$ jest funkcją wypukłą. Jeśli dodatkowo $g$ jest rosnąca, zaś $f$ ściśle wypukła, to $g\circ f$ jest ściśle wypukła.
Niech 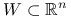$W\subset\mathbb{R}^{n}$ wypukły. Jeśli 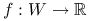$f:W\to\mathbb{R}$ jest funkcją (ściśle) wklęsłą i 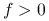$f>0$ , to funkcja 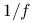$1/f$ jest (ściśle) wypukła.

3.4. Charakteryzacje funkcji wypukłej

Twierdzenie 3.9

Niech $W\subset\mathbb{R}^{n}$ wypukły o niepustym wnętrzu. Jeśli w każdym punkcie ${\bar{\mathbf{x}}}\in\mathop{\rm int}W$ istnieje wektor $\xi\in\mathbb{R}^{n}$ , taki że

$f(\mathbf{x})\ge f(\bar{\mathbf{x}})+\xi^{T}(\mathbf{x}-\bar{\mathbf{x}}),\qquad\forall\,\mathbf{x}\in W,$

to funkcja $f$ jest wypukła. Jeśli nierówność jest ostra dla $\mathbf{x}\ne{\bar{\mathbf{x}}}$ , to $f$ jest ściśle wypukła.

Dowód

Weźmy $\mathbf{x}\in\mathop{\rm int}W$ , $\mathbf{y}\in W$ i $\lambda\in(0,1)$ . Oznaczmy $\mathbf{x}_{\lambda}=\lambda\mathbf{x}+(1-\lambda)\mathbf{y}$ . Chcemy wykazać, że $f(\mathbf{x}_{\lambda})\le\lambda f(\mathbf{x})+(1-\lambda)f(\mathbf{y})$ . Na mocy Lematu 3.2 punkt $\mathbf{x}_{\lambda}$ należy do wnętrza $W$ . Stosując założenie do tego punktu dostajemy $\xi\in\mathbb{R}^{n}$ , takie że

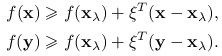$\begin{aligned}\displaystyle f(\mathbf{x})&\displaystyle\ge f(\mathbf{x}_{\lambda})+\xi^{T}(\mathbf{x}-\mathbf{x}_{\lambda}),\\ \displaystyle f(\mathbf{y})&\displaystyle\ge f(\mathbf{x}_{\lambda})+\xi^{T}(\mathbf{y}-\mathbf{x}_{\lambda}).\end{aligned}$

(3.4)

Stąd

$\lambda f(\mathbf{x})+(1-\lambda)f(\mathbf{y})\ge f(\mathbf{x}_{\lambda})+\xi^{T}\big[\lambda(\mathbf{x}-\mathbf{x}_{\lambda})+(1-\lambda)(\mathbf{y}-\mathbf{x}_{\lambda})\big]=f(\mathbf{x}_{\lambda}),$

gdyż wielkości w nawiasie kwadratowym zerują się. Kończy to dowód twierdzenia. Jeśli nierówność w założeniu jest ostra i $\mathbf{x}\ne\mathbf{y}$ , to nierówności (3.4) są ostre i dostajemy warunek ścisłej wypukłości.

∎

Twierdzenie 3.10

Niech $W\subset\mathbb{R}^{n}$ niepusty, otwarty i wypukły, zaś $f:W\to\mathbb{R}$ dwukrotnie różniczkowalna. Wówczas:

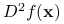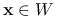I) $f$ jest wypukła wtw, gdy hesjan $D^{2}f(\mathbf{x})$ jest nieujemnie określony dla każdego $\mathbf{x}\in W$ .
II) Jeśli hesjan 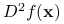$D^{2}f(\mathbf{x})$ jest dodatnio określony dla każdego 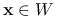$\mathbf{x}\in W$ , to $f$ jest ściśle wypukła.

Analogiczna teza zachodzi w przypadku wklęsłości.

Dowód

Załóżmy najpierw, że hesjan jest nieujemnie określony dla każdego $\mathbf{x}\in W$ . Wówczas, na mocy wniosku 2.1, dla dowolnych ${\bar{\mathbf{x}}},\mathbf{x}\in W$ mamy

$f(\mathbf{x})=f({\bar{\mathbf{x}}})+Df({\bar{\mathbf{x}}})(\mathbf{x}-{\bar{\mathbf{x}}})+\frac{1}{2}(\mathbf{x}-{\bar{\mathbf{x}}})^{T}D^{2}f(\tilde{\mathbf{x}})(\mathbf{x}-{\bar{\mathbf{x}}}),$

gdzie $\tilde{\mathbf{x}}$ jest punktem leżącym na odcinku łączącym ${\bar{\mathbf{x}}}$ z $\mathbf{x}$ . Założenie o nieujemnej określoności hesjanu pociąga nieujemność ostatniego składnika powyższej sumy. Stąd

$f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+Df({\bar{\mathbf{x}}})(\mathbf{x}-{\bar{\mathbf{x}}}).$

(3.5)

Ponieważ powyższa nierówność zachodzi dla dowolnych ${\bar{\mathbf{x}}},\mathbf{x}\in W$ , to $f$ jest wypukła na mocy twierdzenia 3.9.

Jeśli założymy, że hesjan jest dodatnio określony dla każdego punktu $W$ , to nierówność (3.5) jest ostra i twierdzenie 3.9 implikuje ścisłą wypukłość $f$ .

Przejdźmy teraz do dowodu implikacji przeciwnej. Załóżmy, że funkcja $f$ jest wypukła. Ustalmy ${\bar{\mathbf{x}}}\in W$ i $\mathbf{h}\in\mathbb{R}^{n}$ , $\mathbf{h}\ne 0$ . Z otwartości $W$ wynika, że istnieje $\delta>0$ , dla której ${\bar{\mathbf{x}}}+t\mathbf{h}\in W$ , $t\in(-\delta,\delta)$ . Zdefiniujmy funkcję $g(t)=f\big({\bar{\mathbf{x}}}+t\mathbf{h}\big)$ , $t\in(-\delta,\delta)$ . Jest to funkcja jednej zmiennej, dwukrotnie różniczkowalna oraz wypukła. Stosując twierdzenie 3.8 dostajemy

$g(t)\ge g(0)+g^{{\prime}}(0)t,\qquad t\in(-\delta,\delta).$

Na mocy twierdzenie Taylora z resztą w postaci Peano, tw. 1.9, mamy

$g(t)=g(0)+g^{{\prime}}(0)t+\frac{1}{2}g^{{\prime\prime}}(0)t^{2}+o(t^{2}),\qquad t\in(-\delta,\delta).$

Powyższa nierówność i wzór Taylora dają następujące oszacowanie na drugą pochodną

$\frac{1}{2}g^{{\prime\prime}}(0)t^{2}+o(t^{2})\ge 0.$

Dzielimy obie strony przez $t^{2}$ :

$\frac{1}{2}g^{{\prime\prime}}(0)+\frac{o(t^{2})}{t^{2}}\ge 0.$

W granicy przy $t$ dążącym do zera, drugi składnik zanika i pozostaje $g^{{\prime\prime}}(0)\ge 0$ . Co ta nierówność znaczy w terminach funkcji $f$ ? Liczymy:

$g^{{\prime}}(t)=Df({\bar{\mathbf{x}}}+t\mathbf{h})\mathbf{h},\qquad g^{{\prime\prime}}(t)=\mathbf{h}^{T}D^{2}f({\bar{\mathbf{x}}}+t\mathbf{h})\mathbf{h}.$

Stąd $g^{{\prime\prime}}(0)=\mathbf{h}^{T}D^{2}f({\bar{\mathbf{x}}})\mathbf{h}$ .

Powyższe rozumowanie możemy przeprowadzić dla dowolnego $\mathbf{h}\in\mathbb{R}^{n}$ . Wykazaliśmy więc nieujemną określoność $D^{2}f({\bar{\mathbf{x}}})$ .

∎

3.5. Subróżniczka

Zajmiemy się teraz uogólnieniem pojęcia pochodnej na nieróżniczkowalne funkcje wypukłe. Niech $W\subseteq\mathbb{R}^{n}$ będzie zbiorem wypukłym, zaś $f:W\to\mathbb{R}$ funkcją wypukłą.

Definicja 3.4

Wektor $\xi\in\mathbb{R}^{n}$ nazywamy subgradientem funkcji $f$ w punkcie $\mathbf{x}_{0}\in W$ , jeśli

$f(\mathbf{x})\ge f(\mathbf{x}_{0})+\xi^{T}(\mathbf{x}-\mathbf{x}_{0}),\qquad\mathbf{x}\in W.$

Zbiór wszystkich subgradientów $f$ w punkcie $\mathbf{x}_{0}$ nazywamy subróżniczką i oznaczamy $\partial f(\mathbf{x}_{0})$ .

Wniosek 3.3

Jeśli $W\in\mathbb{R}^{n}$ jest zbiorem wypukłym o niepustym wnętrzu, to $f:W\to\mathbb{R}$ jest wypukła wtw, gdy w każdym punkcie zbioru $\mathop{\rm int}W$ istnieje subgradient:

$\partial f(\mathbf{x})\ne\emptyset\qquad\forall\ \mathbf{x}\in\mathop{\rm int}W.$

Dowód

Implikacja w prawą stronę wynika z twierdzenia 3.8, zaś implikacja w stronę lewą – z tw. 3.9.

∎

Lemat 3.3

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym, zaś $f:W\to\mathbb{R}$ funkcją wypukłą. Wówczas subróżniczka $\partial f(\mathbf{x})$ jest zbiorem wypukłym i domkniętym. Jeśli $\mathbf{x}$ jest wewnętrzym punktem $W$ , $\mathbf{x}\in\mathop{\rm int}W$ , to zbiór $\partial f(\mathbf{x})$ jest ograniczony.

Dowód

Dowód wypukłości i domkniętości pozostawiamy jako ćwiczenie (patrz ćw. 3.24). Ustalmy ${\bar{\mathbf{x}}}\in\mathop{\rm int}W$ . Wówczas istnieje $\varepsilon>0$ , taki że kula domknięta $B({\bar{\mathbf{x}}},\varepsilon)$ jest zawarta w $\mathop{\rm int}W$ . Dla dowolnego $\xi\in\partial f({\bar{\mathbf{x}}})$

$f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}}),\qquad\mathbf{x}\in W.$

A zatem

$\sup _{{\mathbf{x}\in B({\bar{\mathbf{x}}},\varepsilon)}}f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+\sup _{{\mathbf{x}\in B({\bar{\mathbf{x}}},\varepsilon)}}\xi^{T}(\mathbf{x}-{\bar{\mathbf{x}}}).$

Lewa strona jest niezależna od $\xi$ oraz, z ciągłości $f$ na $\mathop{\rm int}W$ , skończona. Supremum po prawej stronie jest przyjmowane dla $\mathbf{x}={\bar{\mathbf{x}}}+\varepsilon\xi/\|\xi\|$ i wynosi $\varepsilon\|\xi\|$ . Dostajemy zatem

$\varepsilon\|\xi\|\le\sup _{{\mathbf{x}\in B({\bar{\mathbf{x}}},\varepsilon)}}f(\mathbf{x})-f({\bar{\mathbf{x}}}),$

co dowodzi ograniczoności zbioru $\partial f({\bar{\mathbf{x}}})$ .

∎

Pokażemy teraz związek subróżniczki z pochodnymi kierunkowymi funkcji. Związek ten przyda nam się w dalszych dowodach.

Definicja 3.5

Pochodną kierunkową funkcji $f$ w punkcie ${\bar{\mathbf{x}}}$ w kierunku $\mathbf{d}$ nazywamy granicę

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\lim _{{\lambda\downarrow 0}}\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}.$

Z własności pochodnych jednostronnych dla skalarnych funkcji wypukłych wynikają następujące własności pochodnych kierunkowych:

Lemat 3.4

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym otwartym, zaś $f:W\to\mathbb{R}$ funkcją wypukłą. Wówczas dla każdego $\mathbf{d}\in\mathbb{R}^{n}$ i $\mathbf{x}\in W$

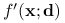I) istnieje pochodna kierunkowa $f^{{\prime}}(\mathbf{x};\mathbf{d})$ .
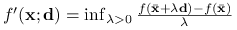II) $f^{{\prime}}(\mathbf{x};\mathbf{d})=\inf _{{\lambda>0}}\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}$ .
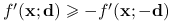III) $f^{{\prime}}(\mathbf{x};\mathbf{d})\ge-f^{{\prime}}(\mathbf{x};-\mathbf{d})$ .

Dowód

Zdefiniujmy funkcję skalarną $g(t)=f(\mathbf{x}+t\mathbf{d})$ dla $t$ , takich że $\mathbf{x}+t\mathbf{d}\in W$ . Z otwartości $W$ wynika, że $g$ jest określona na pewnym otoczeniu zera $(-\delta,\delta)$ . Jest ona także wypukła. Wówczas iloraz różnicowy jest monotoniczny, tzn. dla $-\delta<t_{1}<t_{2}<\delta$ mamy

$\frac{g(t_{1})-g(0)}{t_{1}}\le\frac{g(t_{2})-g(0)}{t_{2}}.$

(3.6)

Z monotoniczności ilorazu różnicowego wynika, że istnieją pochodne lewostronna $g^{{\prime}}(0-)$ i prawostronna $g^{{\prime}}(0+)$ , $g^{{\prime}}(0-)\le g^{{\prime}}(0+)$ oraz

$g^{{\prime}}(0+)=\inf _{{t>0}}\frac{g(t)-g(0)}{t}.$

Wystarczy teraz zauważyć, że $f^{{\prime}}(\mathbf{x};\mathbf{d})=g^{{\prime}}(0+)$ , zaś $f^{{\prime}}(\mathbf{x};-\mathbf{d})=-g^{{\prime}}(0-)$ .

Pozostał nam jeszcze dowód monotoniczności ilorazu różnicowego. Weźmy najpierw $0<t_{1}<t_{2}<\delta$ i zauważmy, że nierówność (3.6) jest równoważna

$g(t_{1})\le\lambda g(t_{2})+(1-\lambda)g(0),$

gdzie $\lambda=t_{1}/t_{2}\in(0,1)$ oraz $\lambda t_{2}+(1-\lambda)0=t_{1}$ . Prawdziwość ostatniej nierówności wynika z wypukłości funkcji $g$ . Przypadek $-\delta<t_{1}<t_{2}<0$ dowodzimy analogicznie. Dla $-\delta<t_{1}<0<t_{2}<\delta$ nierówność (3.6) jest równoważna

$g(0)\le\frac{1}{1+\lambda}g(t_{1})+\frac{\lambda}{1+\lambda}g(t_{2}),\qquad\lambda=-\frac{t_{1}}{t_{2}},$

która wynika z wypukłości $g$ , gdyż $1/(1+\lambda)\in(0,1)$ oraz

$\frac{1}{1+\lambda}t_{1}+\frac{\lambda}{1+\lambda}t_{2}=0.$

∎

Pochodne kierunkowe pozwalają na nową charakteryzację subróżniczki.

Lemat 3.5

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym otwartym, zaś $f:W\to\mathbb{R}$ funkcją wypukłą. Prawdziwa jest następująca równoważność: $\xi\in\partial f({\bar{\mathbf{x}}})$ wtw, gdy

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\ge\xi^{T}\mathbf{d},\qquad\forall\ \mathbf{d}\in\mathbb{R}^{n}.$

Dowód

Ustalmy ${\bar{\mathbf{x}}}\in W$ i $\xi\in\partial f({\bar{\mathbf{x}}})$ . Wówczas dla $\lambda>0$ i $\mathbf{d}\in\mathbb{R}^{n}$ (oczywiście takich, że ${\bar{\mathbf{x}}}+\lambda\mathbf{d}\in W$ ) mamy

$f({\bar{\mathbf{x}}}+\lambda\mathbf{d})\ge f({\bar{\mathbf{x}}})+\lambda\xi^{T}\mathbf{d}.$

Zatem

$\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}\ge\xi^{T}\mathbf{d},$

co implikuje $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\ge\xi^{T}\mathbf{d}$ .

Weźmy teraz wektor $\xi\in\mathbb{R}^{n}$ spełniający warunek $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\ge\xi^{T}\mathbf{d}$ dla każdego $\mathbf{d}\in\mathbb{R}^{n}$ . Na mocy lematu 3.4(II) dla $\lambda>0$ mamy

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\le\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}.$

A zatem

$f({\bar{\mathbf{x}}}+\lambda\mathbf{d})\ge f({\bar{\mathbf{x}}})+\xi^{T}(\lambda\mathbf{d}).$

Z dowolności $\lambda$ i $\mathbf{d}$ wynika, iż $\xi$ jest subgradientem.

∎

Poniższe twierdzenie precyzuje związek pomiędzy subróżniczką i pochodną kierunkową funkcji. Zwróć uwagę na wykorzystanie twierdzenia o oddzielaniu w dowodzie. Metoda polegająca na sprytnym dobraniu rozłącznych zbiorów wypukłych, które można rozdzielić hiperpowierzchnią, będzie wielokrotnie wykorzystywana w dowodzeniu twierdzeń dotyczących funkcji wypukłych.

Twierdzenie 3.11

Niech $f:W\to\mathbb{R}$ będzie funkcją wypukłą zadaną na wypukłym otwartym zbiorze $W\subset\mathbb{R}^{n}$ . Dla dowolnego ${\bar{\mathbf{x}}}\in W$ i $\mathbf{d}\in\mathbb{R}^{n}$ zachodzi

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\max _{{\xi\in\partial f({\bar{\mathbf{x}}})}}\xi^{T}\mathbf{d}.$

Ponadto, funkcja $f$ jest różniczkowalna w ${\bar{\mathbf{x}}}$ wtw, gdy subróżniczka $\partial f({\bar{\mathbf{x}}})$ składa się z jednego subgradientu. Tym subgradientem jest wówczas $Df({\bar{\mathbf{x}}})^{T}$ .

Dowód

Z lematu 3.5 wynika, że $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\ge\xi^{T}\mathbf{d}$ dla $\xi\in\partial f({\bar{\mathbf{x}}})$ . Stąd

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\ge\max _{{\xi\in\partial f({\bar{\mathbf{x}}})}}\xi^{T}\mathbf{d}.$

Udowodnienie przeciwnej nierówności wymaga skorzystania z twierdzenia o oddzielaniu. Zdefiniujmy dwa zbiory:

	$\displaystyle C_{1}$	$\displaystyle=\{(\mathbf{x},z)\in W\times\mathbb{R}:\ z>f(\mathbf{x})\},$
	$\displaystyle C_{2}$	$\displaystyle=\{(\mathbf{x},z)\in W\times\mathbb{R}:\ \mathbf{x}={\bar{\mathbf{x}}}+\lambda\mathbf{d},\ z=f({\bar{\mathbf{x}}})+\lambda f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}),\quad\lambda\ge 0\}.$

Zauważmy, że $C_{1}$ różni się od epigrafu $f$ tylko brzegiem $\{(\mathbf{x},z)\in W\times\mathbb{R}:\ z=f(\mathbf{x})\}$ . Możemy zatem zastosować podobne rozumowanie jak w dowodzie tw. 3.5, aby wykazać, że $C_{1}$ jest zbiorem wypukłym. Zbiór $C_{2}$ jest odcinkiem o początku w punkcie $({\bar{\mathbf{x}}},f({\bar{\mathbf{x}}}))$ i o kierunku $\big(\mathbf{d},f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\big)$ , więc jest wypukły. Można zauważyć, że jest on wykresem liniowego przybliżenia funkcji $f$ wokół punktu ${\bar{\mathbf{x}}}$ wzdłuż odcinka $\{{\bar{\mathbf{x}}}+\lambda\mathbf{d}:\lambda\ge 0\}\cap W$ .

Na mocy lematu 3.4(II) mamy $f^{{\prime}}(\mathbf{x};\mathbf{d})\le\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}$ , czyli

$f({\bar{\mathbf{x}}}+\lambda\mathbf{d})\ge f({\bar{\mathbf{x}}})+\lambda f^{{\prime}}(\mathbf{x};\mathbf{d}).$

Wniskujemy stąd, że zbiory $C_{1}$ i $C_{2}$ są rozłączne. Stosujemy słabe twierdzenie o oddzialniu, tw. 3.1: istnieje niezerowy wektor $(\mu,\gamma)\in\mathbb{R}^{n}\times\mathbb{R}$ , taki że

$\mu^{T}\mathbf{x}+\gamma z\ge\mu^{T}({\bar{\mathbf{x}}}+\lambda\mathbf{d})+\gamma\big(f({\bar{\mathbf{x}}})+\lambda f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\big),\qquad(\mathbf{x},z)\in C_{1},\ \lambda\in[0,L),$

(3.7)

gdzie $L=\sup\{\lambda\ge 0:\ {\bar{\mathbf{x}}}+\lambda\mathbf{d}\in W\}$ . Zauważmy, że $\gamma$ nie może być ujemna, gdyż wtedy lewa strona mogłaby być dowolnie mała ( $z$ może być dowolnie duże). Nie może także być $\gamma=0$ , gdyż wówczas dla każdego $\mathbf{x}\in W$ musiałoby zachodzić $\mu^{T}(\mathbf{x}-{\bar{\mathbf{x}}})\ge\lambda\mu^{T}\mathbf{d}$ . Jest to możliwe tylko, gdy $\mu=\mathbf{0}$ (korzystamy tutaj z faktu, że $W$ jest otwarty). A to przeczy niezerowości wektora $(\mu,\gamma)$ . Dowiedliśmy zatem, że $\gamma>0$ . Dzieląc obie strony nierówności (3.7) przez $\gamma$ możemy założyć, że $\gamma=1$ , czyli

$\mu^{T}\mathbf{x}+z\ge\mu^{T}({\bar{\mathbf{x}}}+\lambda\mathbf{d})+f({\bar{\mathbf{x}}})+\lambda f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}),\qquad(\mathbf{x},z)\in C_{1},\ \lambda\in[0,L).$

Zbiegając z $z$ do $f(\mathbf{x})$ otrzymujemy

$\mu^{T}\mathbf{x}+f(\mathbf{x})\ge\mu^{T}({\bar{\mathbf{x}}}+\lambda\mathbf{d})+f({\bar{\mathbf{x}}})+\lambda f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}),\qquad\mathbf{x}\in W,\ \lambda\in[0,L).$

(3.8)

Kładąc $\lambda=0$ dostajemy

$\mu^{T}(\mathbf{x}-{\bar{\mathbf{x}}})+f(\mathbf{x})\ge f({\bar{\mathbf{x}}}),$

co po przekształeceniu daje

$f(\mathbf{x})\ge f({\bar{\mathbf{x}}})-\mu^{T}(\mathbf{x}-{\bar{\mathbf{x}}}).$

A zatem $-\mu\in\partial f({\bar{\mathbf{x}}})$ . Biorąc w nierówności (3.8) $\lambda>0$ i $\mathbf{x}={\bar{\mathbf{x}}}$ dostajemy

$-\mu^{T}(\lambda\mathbf{d})\ge\lambda f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}),$

czyli

$\sup _{{\xi\in\partial f({\bar{\mathbf{x}}})}}\xi^{T}\mathbf{d}\ge f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}).$

To kończy dowód pierwszej części twierdzenia.

Dowód drugiej części twierdzenia opiera się na dwóch prostych równoważnościach:

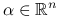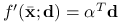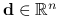Funkcja $f$ jest różniczkowalna w punkcie ${\bar{\mathbf{x}}}$ wtw, gdy istnieje wektor $\alpha\in\mathbb{R}^{n}$ , taki że $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\alpha^{T}\mathbf{d}$ dla każdego $\mathbf{d}\in\mathbb{R}^{n}$ .
Odwzorowanie 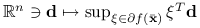$\mathbb{R}^{n}\ni\mathbf{d}\mapsto\sup _{{\xi\in\partial f({\bar{\mathbf{x}}})}}\xi^{T}\mathbf{d}$ jest liniowe wtw, gdy subróżniczka 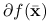$\partial f({\bar{\mathbf{x}}})$ jest jednoelementowa.

Równoważność pierwsza wynika wprost z definicji pochodnej (patrz roz. 2). Jeśli $f$ jest różniczowalna w ${\bar{\mathbf{x}}}$ , jedynym wektorem spełniającym $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\alpha^{T}\mathbf{d}$ jest $\alpha=Df({\bar{\mathbf{x}}})^{T}$ .

Przypuśćmy więc, że funkcja $f$ jest różniczkowalna w ${\bar{\mathbf{x}}}$ . Wówczas $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=Df({\bar{\mathbf{x}}})\mathbf{d}$ , czyli pochodna kierunkowa jest funkcją liniową $\mathbf{d}$ . Na mocy drugiej równoważności subróżniczka jest jednoelementowa. Łatwo już zauważyć, że $\partial f({\bar{\mathbf{x}}})=\{ Df({\bar{\mathbf{x}}})^{T}\}$ . Do dowodu w przeciwną stronę załóżmy, że subróżniczka $\partial f({\bar{\mathbf{x}}})$ składa się z jednego wektora $\alpha\in\mathbb{R}^{n}$ . Wówczas $f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\alpha^{T}\mathbf{d}$ . Na mocy pierwszej równoważności funkcja $f$ jest różniczkowalna w ${\bar{\mathbf{x}}}$ .

∎

Twierdzenie 3.11 wykorzystamy kilkukrotnie w dowodzie poniższego twierdzenia, które będzie użyteczne w znajdowaniu subróżniczek.

Twierdzenie 3.12

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym otwartym, zaś $f_{1},f_{2}:W\to\mathbb{R}$ funkcjami wypukłymi.

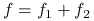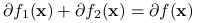I) Niech $f=f_{1}+f_{2}$ . Wówczas $\partial f_{1}(\mathbf{x})+\partial f_{2}(\mathbf{x})=\partial f(\mathbf{x})$ , gdzie

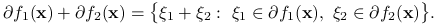
$\partial f_{1}(\mathbf{x})+\partial f_{2}(\mathbf{x})=\big\{\xi _{1}+\xi _{2}:\ \xi _{1}\in\partial f_{1}(\mathbf{x}),\ \xi _{2}\in\partial f_{2}(\mathbf{x})\big\}.$
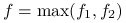II) Niech $f=\max(f_{1},f_{2})$ . Wówczas

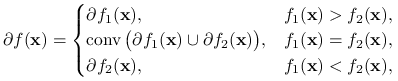
$\partial f(\mathbf{x})=\begin{cases}\partial f_{1}(\mathbf{x}),&f_{1}(\mathbf{x})>f_{2}(\mathbf{x}),\\ \mathop{\rm conv}\big(\partial f_{1}(\mathbf{x})\cup\partial f_{2}(\mathbf{x})\big),&f_{1}(\mathbf{x})=f_{2}(\mathbf{x}),\\ \partial f_{2}(\mathbf{x}),&f_{1}(\mathbf{x})<f_{2}(\mathbf{x}),\end{cases}$

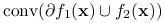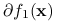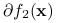gdzie $\mathop{\rm conv}(\partial f_{1}(\mathbf{x})\cup f_{2}(\mathbf{x}))$ jest zbiorem kombinacji wypukłych elementów zbiorów $\partial f_{1}(\mathbf{x})$ i $\partial f_{2}(\mathbf{x})$ .

Dowód

Zaczniemy od dowodu (I). Ustalmy ${\bar{\mathbf{x}}}\in W$ . Niech $\xi _{1}\in\partial f_{1}({\bar{\mathbf{x}}})$ i $\xi _{2}\in\partial f_{2}({\bar{\mathbf{x}}})$ . Wówczas dla $\mathbf{x}\in W$ zachodzi

	$\displaystyle f_{1}(\mathbf{x})$	$\displaystyle\ge f_{1}({\bar{\mathbf{x}}})+\xi _{1}^{T}(\mathbf{x}-{\bar{\mathbf{x}}}),$
	$\displaystyle f_{2}(\mathbf{x})$	$\displaystyle\ge f_{2}({\bar{\mathbf{x}}})+\xi _{2}^{T}(\mathbf{x}-{\bar{\mathbf{x}}}).$

Dodając te nierówności stronami otrzymujemy

$f(\mathbf{x})\ge f({\bar{\mathbf{x}}})+(\xi _{1}+\xi _{2})^{T}(\mathbf{x}-{\bar{\mathbf{x}}}),$

czyli $\xi _{1}+\xi _{2}\in\partial f({\bar{\mathbf{x}}})$ . Dowiedliśmy zawierania $\partial f_{1}({\bar{\mathbf{x}}})+\partial f_{2}({\bar{\mathbf{x}}})\subset\partial f({\bar{\mathbf{x}}})$ . Przypuśćmy, że inkluzja ta jest ostra, tzn. istnieje $\xi\in\partial f({\bar{\mathbf{x}}})$ , taki że $\xi\notin\partial f_{1}({\bar{\mathbf{x}}})+\partial f_{2}({\bar{\mathbf{x}}})$ . Na mocy lematu 3.3 subróżniczki $\partial f_{1}({\bar{\mathbf{x}}})$ i $\partial f_{2}({\bar{\mathbf{x}}})$ są zwartymi zbiorami wypukłymi. A zatem ich suma algebraiczna jest również zbiorem zwartym i wypukłym (patrz ćw. 3.25). Stosujemy silne twierdzenie o oddzielaniu do zbiorów $\{\xi\}$ oraz $\partial f_{1}({\bar{\mathbf{x}}})+\partial f_{2}({\bar{\mathbf{x}}})$ . Dostajemy $\mu\in\mathbb{R}^{n}$ i stałą $b\in R$ , takie że

$\mu^{T}\xi _{1}+\mu^{T}\xi _{2}<b<\mu^{T}\xi,\qquad\forall\ \xi _{1}\in\partial f_{1}({\bar{\mathbf{x}}}),\ \xi _{2}\in\partial f_{2}({\bar{\mathbf{x}}}).$

Bierzemy maksimum po $\xi _{1},\xi _{2}$ po lewej stronie i stosujemy twierdzenie 3.11:

$f_{1}^{{\prime}}({\bar{\mathbf{x}}};\mu)+f_{2}^{{\prime}}({\bar{\mathbf{x}}};\mu)<\xi^{T}\mu\le f^{{\prime}}({\bar{\mathbf{x}}};\mu).$

Z drugiej strony, z własności pochodnych kierunkowych mamy

$f_{1}^{{\prime}}({\bar{\mathbf{x}}};\mu)+f_{2}^{{\prime}}({\bar{\mathbf{x}}};\mu)=f^{{\prime}}({\bar{\mathbf{x}}};\mu).$

Doprowadziliśmy do sprzeczności: $\xi$ o żądanych własnościach nie może istnieć. Kończy to dowód (I).

Dowód (II). Postać subróżniczki $\partial f$ na zbiorach $\{\mathbf{x}\in W:\ f_{1}(\mathbf{x})>f_{2}(\mathbf{x})\}$ i $\{\mathbf{x}\in W:\ f_{1}(\mathbf{x})<f_{2}(\mathbf{x})\}$ jest oczywista. Jedynie przypadek $\{\mathbf{x}\in W:\ f_{1}(\mathbf{x})=f_{2}(\mathbf{x})\}$ wymaga dokładnego dowodu. Ustalmy ${\bar{\mathbf{x}}}\in W$ , dla którego $f_{1}({\bar{\mathbf{x}}})=f_{2}({\bar{\mathbf{x}}})$ . Oznaczmy $A=\mathop{\rm conv}\big(\partial f_{1}({\bar{\mathbf{x}}})\cup\partial f_{2}({\bar{\mathbf{x}}})\big)$ . Dla $i=1,2$ oraz $\mathbf{x}\in W$ mamy

$f(\mathbf{x})-f({\bar{\mathbf{x}}})\ge f_{i}(\mathbf{x})-f({\bar{\mathbf{x}}})=f_{i}(\mathbf{x})-f_{i}({\bar{\mathbf{x}}})\ge\xi _{i}^{T}(\mathbf{x}-{\bar{\mathbf{x}}}),\qquad\forall\ \xi _{i}\in\partial f_{i}({\bar{\mathbf{x}}}).$

Stąd dostajemy $\partial f_{1}({\bar{\mathbf{x}}})\cup\partial f_{1}({\bar{\mathbf{x}}})\subset\partial f({\bar{\mathbf{x}}})$ . Z wypukłości subróżniczki (patrz lemat 3.3) wynika, że $A\subset\partial f({\bar{\mathbf{x}}})$ . Załóżmy teraz, że istnieje $\xi\in\partial f({\bar{\mathbf{x}}})\setminus A$ . Zbiór $A$ jest wypukły i zwarty. Stosujemy silne twierdzenie o oddzielaniu do zbiorów $A$ i $\{\xi\}$ . Dostajemy $\mu\in\mathbb{R}^{n}$ i stałą $b\in R$ , takie że

$\mu^{T}\tilde{\xi}<b<\mu^{T}\xi,\qquad\forall\ \tilde{\xi}\in A.$

W szczególności $\mu^{T}\xi _{i}<b$ dla $\xi _{i}\in\partial f_{i}({\bar{\mathbf{x}}})$ , $i=1,2$ , czyli, na mocy tw. 3.11,

$\max\big(f_{1}^{{\prime}}({\bar{\mathbf{x}}};\mu),f_{2}^{{\prime}}({\bar{\mathbf{x}}};\mu)\big)\le b.$

Podobnie, $b<\xi^{T}\mu\le f^{{\prime}}({\bar{\mathbf{x}}};\mu)$ . Podsumowując:

$\max\big(f_{1}^{{\prime}}({\bar{\mathbf{x}}};\mu),f_{2}^{{\prime}}({\bar{\mathbf{x}}};\mu)\big)<f^{{\prime}}({\bar{\mathbf{x}}};\mu).$

(3.9)

Z drugiej strony, definicja pochodnej kierunkowej daje nam następującą równość (przypomnijmy, że $f({\bar{\mathbf{x}}})=f_{1}({\bar{\mathbf{x}}})=f_{2}({\bar{\mathbf{x}}})$ ):

$\frac{f({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}=\max\bigg(\frac{f_{1}({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda},\frac{f_{2}({\bar{\mathbf{x}}}+\lambda\mathbf{d})-f({\bar{\mathbf{x}}})}{\lambda}\bigg),\qquad\lambda>0.$

Przechodząc z $\lambda$ do zera dostajemy

$f^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=\max\big(f_{1}^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d}),f_{2}^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})\big).$

Biorąc $\mathbf{d}=\mu$ dostajemy sprzeczność z (3.9), a więc nie może istnieć $\xi\in\partial f({\bar{\mathbf{x}}})\setminus A$ .

∎

Twierdzenie 3.13

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym otwartym, $f:W\to\mathbb{R}$ funkcją wypukłą, zaś $A$ będzie macierzą $n\times m$ . Zdefiniujmy $\tilde{W}=\{\mathbf{x}\in\mathbb{R}^{m}:A\mathbf{x}\in W\}$ . Wówczas $\tilde{W}$ jest zbiorem wypukłym otwartym oraz funkcja $F:\tilde{W}\to\mathbb{R}$ zadana wzorem $F(\mathbf{x})=f(A\mathbf{x})$ ma w punkcie $\mathbf{x}\in\tilde{W}$ subróżniczkę zadaną wzorem

$\partial F(\mathbf{x})=A^{T}\partial f(A\mathbf{x}).$

Dowód

Dowód będzie przebiegał podobnie jak dowód poprzedniego twierdzenia. Ustalmy ${\bar{\mathbf{x}}}\in\tilde{W}$ . Weźmy $\xi\in\partial f(A{\bar{\mathbf{x}}})$ . Wówczas

$f(A\mathbf{x})\ge f(A{\bar{\mathbf{x}}})+\xi^{T}(A\mathbf{x}-A{\bar{\mathbf{x}}})=f(A{\bar{\mathbf{x}}})+(A^{T}\xi)^{T}(\mathbf{x}-{\bar{\mathbf{x}}}),$

czyli $A^{T}\xi\in\partial F({\bar{\mathbf{x}}})$ . Stąd mamy zawieranie $A^{T}\partial f(A{\bar{\mathbf{x}}})\subset\partial F({\bar{\mathbf{x}}})$ . Równości tych dwóch zbiorów dowiedziemy przez sprzeczność. Załóżmy, że istnieje $\xi\in\partial F({\bar{\mathbf{x}}})\setminus A^{T}\partial f(A{\bar{\mathbf{x}}})$ . Zbiór $A^{T}\partial f(A{\bar{\mathbf{x}}})$ jest wypukły i domknięty, jako liniowy obraz zbioru wypukłego i domkniętego. Zastosujemy silne twierdzenie o oddzielaniu, aby oddzielić go od zbioru jednoelementowego $\{\xi\}$ . Dostajemy $\mu\in\mathbb{R}^{m}$ oraz $b\in\mathbb{R}$ , takie że

$\mu^{T}A^{T}\tilde{\xi}<b<\mu^{T}\xi,\qquad\forall\ \tilde{\xi}\in\partial f(A{\bar{\mathbf{x}}}).$

Biorąc supremum po $\tilde{\xi}\in\partial f(A{\bar{\mathbf{x}}})$ po lewej stronie i stosując tw. 3.11 otrzymujemy $f^{{\prime}}(A{\bar{\mathbf{x}}};A\mu)\le b$ . Prawą stronę możemy również oszacować przez pochodną kierunkową: $\mu^{T}\xi\le F^{{\prime}}({\bar{\mathbf{x}}};\mu)$ . Podsumowując:

$f^{{\prime}}(A{\bar{\mathbf{x}}};A\mu)<F^{{\prime}}({\bar{\mathbf{x}}};\mu).$

Jednak z własności pochodnych kierunkowych natychmiast wnioskujemy, że $F^{{\prime}}({\bar{\mathbf{x}}};\mathbf{d})=f^{{\prime}}(A{\bar{\mathbf{x}}};A\mathbf{d})$ dla dowolnego $\mathbf{d}\in\mathbb{R}^{m}$ . Mamy zatem sprzeczność. Dowodzi to, iż zbiór $\partial F({\bar{\mathbf{x}}})\setminus A^{T}\partial f(A{\bar{\mathbf{x}}})$ jest pusty.

∎

3.6. Zadania

Ćwiczenie 3.1

Niech $U,V\subset\mathbb{R}^{n}$ będą zbiorami wypukłymi. Wykaż, że

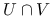$U\cap V$ jest zbiorem wypukłym.
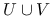$U\cup V$ może nie być zbiorem wypukłym.

Ćwiczenie 3.2

Czy zbiór $\{(x_{1},x_{2},x_{3})\in\mathbb{R}^{3}:\ x_{1}^{6}+x_{1}^{2}+x_{2}x_{3}+x_{3}^{2}\le 1\}$ jest zbiorem wypukłym?

Ćwiczenie 3.3

Udowodnij lemat 3.1.

Ćwiczenie 3.4

Niech

$W_{1}=\{(x_{1},x_{2}):\ x_{2}\ge e^{{-x_{1}}}\},\qquad W_{2}=\{(x_{1},x_{2}):\ x_{2}\le-e^{{-x_{1}}}\}.$

Wykaż, że zbiory $W_{1},W_{2}$ są wypukłe i rozłączne. Znajdź prostą (hiperpłaszczyznę) je dzielącą. Czy istnieje hiperpłaszczyzna dzieląca ściśle te zbiory (w sensie mocnego twierdzenia o oddzielaniu)?

Ćwiczenie 3.5

Niech $W_{1},W_{2}\subset\mathbb{R}^{n}$ będą zbiorami wypukłymi. Udowodnij, że $\inf\{\|\mathbf{x}-\mathbf{y}\|:\ \mathbf{x}\in W_{1},\quad\mathbf{y}\in W_{2}\}>0$ wtw, gdy istnieje hiperpłaszczyzna ściśle (w sensie mocnego tw. o oddzielaniu) oddzielająca te zbiory.

Ćwiczenie 3.6

Niech $\mathbb{X}\subset\mathbb{R}^{n}$ będzie dowolnym zbiorem. Zdefiniujmy zbiór $\tilde{\mathbb{X}}$ jako zbiór takich punktów $\mathbf{x}\in\mathbb{R}^{n}$ , dla których istnieje liczba naturalna $m\in\mathbb{N}$ , zależna od punktu, wektor $[\lambda _{1},\ldots,\lambda _{m}]\in[0,1]^{m}$ o tej własności, że $\sum _{{i=1}}^{m}\lambda _{i}=1$ , oraz $\mathbf{x}_{1},\ldots,\mathbf{x}_{m}\in\mathbb{X}$ i

$\mathbf{x}=\sum _{{i=1}}^{m}\lambda _{i}\mathbf{x}_{i}.$

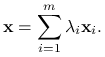Udowodnij, że

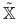$\tilde{\mathbb{X}}$ jest zbiorem wypukłym.
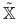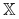$\tilde{\mathbb{X}}$ jest najmniejszym zbiorem wypukłym zawierającym $\mathbb{X}$ .
W definicji zbioru 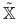$\tilde{\mathbb{X}}$ można założyć, że 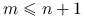$m\le n+1$ , gdzie 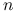$n$ jest wymiarem przestrzeni (Tw. Caratheodory'ego).

Zbiór $\tilde{X}$ nazywa się otoczką wypukłą zbioru $\mathbb{X}$ i oznaczane jest $\text{conv}(\mathbb{X})$ .

Ćwiczenie 3.7

Udowodnij twierdzenie 3.5.

Ćwiczenie 3.8

Udowodnij twierdzenie 3.6.

Ćwiczenie 3.9

Znajdź przykład zbioru $W\subseteq\mathbb{R}^{n}$ i funkcji wypukłej $f:W\to\mathbb{R}$ , która nie jest ciągła na całym zbiorze $W$ .

Wskazówka:

Twierdzenie 3.7 pomoże w wyborze zbioru $W$ .

Ćwiczenie 3.10

Niech $W\subseteq\mathbb{R}^{n}$ będzie zbiorem wypukłym i otwartym, zaś $f:W\to\mathbb{R}$ funkcją różniczkowalną. Udowodnij następującą równoważność: $f$ jest wypukła wtw, gdy

$\big(Df(\mathbf{y})-Df(\mathbf{x})\big)(\mathbf{y}-\mathbf{x})\ge 0,\qquad\forall\,\mathbf{x},\mathbf{y}\in W.$

Ćwiczenie 3.11

Udowodnij: Niech $W\subset\mathbb{R}^{n}$ , wypukły, zaś $I$ dowolny zbiór. Jeśli funkcje $f_{i}:W\to\mathbb{R}$ , $i\in I$ , są wypukłe, to $f(\mathbf{x})=\sup _{{i\in I}}f_{i}(\mathbf{x})$ jest wypukła ze zbiorem wartości $\mathbb{R}\cup\{\infty\}$ .

Ćwiczenie 3.12

Udowodnij: Niech $W\subset\mathbb{R}^{n}$ , wypukły. Jeśli funkcje $f_{i}:W\to\mathbb{R}$ , $i=1,2,\ldots,m$ , są wypukłe i $\alpha _{i}>0$ dla $i=1,2,\ldots,m$ , to funkcja $f=\sum _{{i=1}}^{m}\alpha _{i}f_{i}$ jest wypukła. Jeśli jedna z funkcji $f_{i}$ jest ściśle wypukła, to $f$ jest również ściśle wypukła.

Ćwiczenie 3.13

Udowodnij: Niech $W\subset\mathbb{R}^{n}$ , wypukły, zaś $A\subset\mathbb{R}^{m}$ wypukły, zwarty. Jeśli funkcja $h:W\times A\to\mathbb{R}$ jest wypukła i ciągła, to

$f(\mathbf{x})=\inf _{{\mathbf{a}\in A}}h(\mathbf{x},\mathbf{a}),\qquad\mathbf{x}\in W,$

jest wypukła.

Wskazówka:

Korzystając ze zwartości $A$ i ciągłości $h$ , dla każdego $\mathbf{x}$ istnieje $\mathbf{a}(\mathbf{x})\in A$ realizujący infimum. Dowodzimy teraz z definicji funkcji wypukłej.

Ćwiczenie 3.14

Udowodnij uogólnienie twierdzenia z ćwiczenia 3.13: opuścimy zwartość $A$ i ciągłość $h$ . Niech $W\subset\mathbb{R}^{n}$ , $A\subset\mathbb{R}^{m}$ wypukłe zbiory. Jeśli funkcja $h:W\times A\to\mathbb{R}$ jest wypukła i ograniczona z dołu, to

$f(\mathbf{x})=\inf _{{\mathbf{a}\in A}}h(\mathbf{x},\mathbf{a}),\qquad\mathbf{x}\in W,$

jest wypukła.

Ćwiczenie 3.15

Skonstruuj przykład, który pokaże, że założenie o ograniczoności z dołu nie może być pominięte w twierdzeniu z ćw. 3.14.

Ćwiczenie 3.16

Udowodnij, że funkcja odległości od zbioru wypukłego jest funkcją wypukłą. Podaj przykład wskazujący na konieczność wypukłości zbioru.

Ćwiczenie 3.17

Udowodnij: Niech $f:\mathbb{R}^{n}\to\mathbb{R}$ wypukła. Jeśli $h:\mathbb{R}^{m}\to\mathbb{R}^{n}$ afiniczna, to złożenie $f\circ h$ jest funkcją wypukłą.

Ćwiczenie 3.18

Udowodnij: Niech $W\subset\mathbb{R}^{n}$ , wypukły. Jeśli $f:W\to\mathbb{R}$ jest funkcją wypukłą i $g:\mathbb{R}\to\mathbb{R}$ jest wypukła i niemalejąca, to $g\circ f$ jest funkcją wypukłą. Kiedy $g\circ f$ jest ściśle wypukła?

Stwórz analog powyższego twierdzenia dla funkcji wklęsłych.

Ćwiczenie 3.19

Udowodnij: Niech $W\subset\mathbb{R}^{n}$ wypukły. Jeśli $f:W\to\mathbb{R}$ jest funkcją (ściśle) wklęsłą i $f>0$ , to funkcja $1/f$ jest (ściśle) wypukła.

Ćwiczenie 3.20

Czy jeśli $f:\mathbb{R}^{n}\to\mathbb{R}$ i $g:\mathbb{R}\to\mathbb{R}$ wypukłe, to $g\circ f:\mathbb{R}^{n}\to\mathbb{R}$ jest wypukła?

Ćwiczenie 3.21

Udowodnij, że funkcja $f(x_{1},x_{2})=e^{{x_{1}^{2}-x_{2}}}$ jest wypukła.

Ćwiczenie 3.22

Niech $W\subset\mathbb{R}^{n}$ i funkcja $f:W\to\mathbb{R}$ klasy $C^{2}$ . Załóżmy ponadto, że $D^{2}f(\mathbf{x})\ge 0$ dla każdego $\mathbf{x}\in W$ (tzn. Hesjan jest nieujemnie określony). Rozstrzygnij, który z następujących warunków jest wystarczający, by zdanie

$Df({\bar{\mathbf{x}}})=\mathbf{0}\qquad\implies\qquad\text{w ${\bar{\mathbf{x}}}$ jest globalne minimum}$

było prawdziwe:

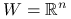$W=\mathbb{R}^{n}$ ,
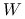$W$ jest wypukły i otwarty,
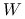$W$ jest wypukły,
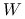$W$ jest otwarty.

Ćwiczenie 3.23

Znajdź przykład zbioru $\mathbb{X}\subset\mathbb{R}^{n}$ oraz funkcji $f:\mathbb{X}\to\mathbb{R}$ klasy $C^{2}$ , takiej że

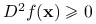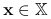$D^{2}f(\mathbf{x})\ge 0$ (tzn. hesjan jest nieujemnie określony) dla każdego $\mathbf{x}\in\mathbb{X}$ ,
istnieje punkt 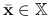${\bar{\mathbf{x}}}\in\mathbb{X}$ , w którym jest minimum lokalne funkcji $f$ , ale nie jest ono globalne.

Ćwiczenie 3.24

Niech $W\subset\mathbb{R}^{n}$ będzie zbiorem wypukłym, zaś $f:W\to\mathbb{R}$ funkcją wypukłą. Udowodnij, że $\partial f(\mathbf{x})$ jest zbiorem wypukłym i domkniętym.

Ćwiczenie 3.25

Niech $A,B\subset\mathbb{R}^{n}$ będą zbiorami wypukłymi zwartymi. Udowodnij, że suma algebraiczna tych zbiorów

$A+B=\{\mathbf{a}+\mathbf{b}:\ \mathbf{a}\in A,\ \mathbf{b}\in B\}$

jest zbiorem zwartym i wypukłym.

Ćwiczenie 3.26

Niech $W\subset\mathbb{R}^{n}$ wypukły otwarty i $f:W\to\mathbb{R}$ wypukła. Wykaż, że $\xi\in\mathbb{R}^{n}$ jest subgradientem $f$ w ${\bar{\mathbf{x}}}\in W$ wtw, gdy odwzorowanie $\mathbf{x}\mapsto\xi^{T}\mathbf{x}-f(\mathbf{x})$ osiąga swoje maksimum w ${\bar{\mathbf{x}}}$ .

Ćwiczenie 3.27

Znajdź subróżniczkę funkcji $\mathbb{R}^{n}\ni\mathbf{x}\mapsto\|\mathbf{x}\|$ .

Ćwiczenie 3.28

Niech $A$ będzie macierzą $n\times n$ symetryczną i nieujemnie określoną. Udowodnij, że $f(\mathbf{x})=\sqrt{\mathbf{x}^{T}A\mathbf{x}}$ , $\mathbf{x}\in\mathbb{R}^{n}$ , jest funkcją wypukłą i znajdź jej subróżniczkę.

Ćwiczenie 3.29

Wykaż, że dla skalarnej funkcji wypukłej $f:(a,b)\to\mathbb{R}$ mamy

$\partial f(x)=[f^{{\prime}}(x-),f^{{\prime}}(x+)],$

gdzie $f^{{\prime}}(x\pm)$ oznaczają prawo- i lewo-stronne pochodne w punkcie $x\in(a,b)$ .

Ćwiczenie 3.30

Niech $f:\mathbb{R}^{n}\to\mathbb{R}$ wypukła, $\mathbf{x},\mathbf{y}\in\mathbb{R}^{n}$ ustalone wektory. Zdefiniujmy $g(t)=f(t\mathbf{x}+(1-t)\mathbf{y})$ , $t\in\mathbb{R}$ . Wykaż, że $g$ jest wypukła oraz

$\partial g(t)=(\mathbf{x}-\mathbf{y})^{T}\partial f\big(t\mathbf{x}+(1-t)\mathbf{y}\big).$

Ćwiczenie 3.31

Wykaż, że funkcja $f(x)=\max(-2x+5,3x^{2}-1)$ jest wypukła na $\mathbb{R}$ i znajdź jej subróżniczkę.

Ćwiczenie 3.32

Niech $f_{W}(\mathbf{x})=\inf _{{\mathbf{y}\in W}}\| x-y\|$ , $\mathbf{x}\in\mathbb{R}^{n}$ , gdzie $W\subset\mathbb{R}^{n}$ jest zbiorem wypukłym. Znajdź subróżniczkę w następujących przypadkach:

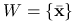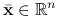$W=\{{\bar{\mathbf{x}}}\}$ dla pewnego ${\bar{\mathbf{x}}}\in\mathbb{R}^{n}$ ,
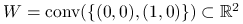$W=\mathop{\rm conv}(\{(0,0),(1,0)\})\subset\mathbb{R}^{2}$ , tzn. 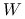$W$ jest odcinkiem,
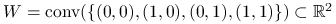$W=\mathop{\rm conv}(\{(0,0),(1,0),(0,1),(1,1)\})\subset\mathbb{R}^{2}$ , tzn. 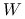$W$ jest kwadratem.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Optymalizacja II

Zagadnienia

3. Funkcje wypukłe

3.1. Zbiory wypukłe i twierdzenia o oddzielaniu

Lemat 3.1

Lemat 3.2

Dowód

Twierdzenie 3.1 (Słabe twierdzenie o oddzielaniu)

Wniosek 3.1

Twierdzenie 3.2 (Mocne twierdzenie o oddzielaniu)

Uwaga 3.1

Dowód twierdzenia 3.2

Dowód twierdzenia 3.1

3.2. Definicja funkcji wypukłej

Definicja 3.1

Twierdzenie 3.3

Dowód

Twierdzenie 3.4

Dowód

Przykład 3.1

3.3. Własności funkcji wypukłych

Definicja 3.2

Definicja 3.3

Twierdzenie 3.5 (Twierdzenie o epigrafie)

Twierdzenie 3.6

Uwaga 3.2

Twierdzenie 3.7

Twierdzenie 3.8 (Twierdzenie o hiperpłaszczyźnie podpierającej)

Dowód tw. 3.8

Wniosek 3.2

Dowód

3.4. Charakteryzacje funkcji wypukłej

Twierdzenie 3.9

Dowód

Twierdzenie 3.10

Dowód

3.5. Subróżniczka

Definicja 3.4

Wniosek 3.3

Dowód

Lemat 3.3

Dowód

Definicja 3.5

Lemat 3.4

Dowód

Lemat 3.5

Dowód

Twierdzenie 3.11

Dowód

Twierdzenie 3.12

Dowód

Twierdzenie 3.13

Dowód

3.6. Zadania

Ćwiczenie 3.1

Ćwiczenie 3.2

Ćwiczenie 3.3

Ćwiczenie 3.4

Ćwiczenie 3.5

Ćwiczenie 3.6

Ćwiczenie 3.7

Ćwiczenie 3.8

Ćwiczenie 3.9

Ćwiczenie 3.10

Ćwiczenie 3.11

Ćwiczenie 3.12

Ćwiczenie 3.13

Ćwiczenie 3.14

Ćwiczenie 3.15

Ćwiczenie 3.16

Ćwiczenie 3.17

Ćwiczenie 3.18

Ćwiczenie 3.19

Ćwiczenie 3.20

Ćwiczenie 3.21

Ćwiczenie 3.22

Ćwiczenie 3.23

Ćwiczenie 3.24

Ćwiczenie 3.25

Ćwiczenie 3.26