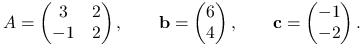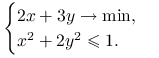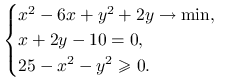Zagadnienia
4. Ekstrema funkcji wypukłej z ograniczeniami
4.1. Problem minimalizacyjny
Niech ![]() będzie niepustym wypukłym podzbiorem
będzie niepustym wypukłym podzbiorem ![]() , zaś
, zaś ![]() będzie funkcją wypukłą. Rozważmy problem minimalizacji funkcji
będzie funkcją wypukłą. Rozważmy problem minimalizacji funkcji ![]() na zbiorze
na zbiorze ![]() :
:
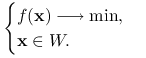 |
(4.1) |
Przypomnijmy, że punktami dopuszczalnymi nazywamy elementy zbioru ![]() . Rozwiązaniem globalnym nazywamy taki punkt
. Rozwiązaniem globalnym nazywamy taki punkt ![]() , że
, że ![]() dla każdego
dla każdego ![]() . Rozwiązaniem lokalnym jest taki punkt
. Rozwiązaniem lokalnym jest taki punkt ![]() , że istnieje
, że istnieje ![]() , dla którego
, dla którego ![]() , jeśli
, jeśli ![]() . Rozwiązanie jest ścisłe, jeśli
. Rozwiązanie jest ścisłe, jeśli ![]() dla
dla ![]() i
i ![]() . Innymi słowy,
. Innymi słowy, ![]() jest rozwiązaniem lokalnym, jeśli
jest rozwiązaniem lokalnym, jeśli ![]() jest minimum funkcji
jest minimum funkcji ![]() na pewnym otoczeniu
na pewnym otoczeniu ![]() .
.
Twierdzenie 4.1
Niech ![]() wypukły,
wypukły, ![]() wypukła. Jeśli
wypukła. Jeśli ![]() będzie rozwiązaniem lokalnym (4.1), to:
będzie rozwiązaniem lokalnym (4.1), to:
I)
 jest rozwiązaniem globalnym,
jest rozwiązaniem globalnym,II) Zbiór rozwiązań globalnych jest wypukły.
III) Jeśli
 jest ściśle wypukła, to
jest ściśle wypukła, to  jest ścisłym rozwiązaniem lokalnym.
jest ścisłym rozwiązaniem lokalnym.IV) Jeśli
 jest ścisłym rozwiązaniem lokalnym, to
jest ścisłym rozwiązaniem lokalnym, to  jest jedynym rozwiązaniem globalnym.
jest jedynym rozwiązaniem globalnym.
Zauważmy, że w powyższym twierdzeniu nie zakładamy różniczkowalności funkcji ![]() .
.
Dowód twierdzenia 4.1
(I): Dowód przez sprzeczność. Przypuśćmy, że istnieje ![]() takie że
takie że ![]() . Ponieważ
. Ponieważ ![]() jest rozwiązaniem lokalnym, to
jest rozwiązaniem lokalnym, to ![]() dla
dla ![]() i
i ![]() . Z wypukłości zbioru
. Z wypukłości zbioru ![]() wynika, iż odcinek łączący
wynika, iż odcinek łączący ![]() i
i ![]() znajduje się w zbiorze
znajduje się w zbiorze ![]() . Ma on więc niepuste przecięcie z kulą
. Ma on więc niepuste przecięcie z kulą ![]() : dla pewnego
: dla pewnego ![]() mamy
mamy ![]() . Z wypukłości
. Z wypukłości ![]() dostajemy
dostajemy
co przeczy lokalnej optymalności ![]() .
.
(II) Pozostawione jako ćwiczenie.
(III) Wynika wprost z definicji ścisłej wypukłości.
(IV) Pozostawione jako ćwiczenie.
∎Dotychczas pokazaliśmy, że warunkiem koniecznym i dostatecznym minimum funkcji wypukłej na zbiorze wypukłym i otwartym jest zerowanie się pochodnej/gradientu. Uogólnimy teraz te wyniki na przypadek dowolnych zbiorów wypukłych.
Twierdzenie 4.2
Niech ![]() wypukły,
wypukły, ![]() wypukła. Jeśli
wypukła. Jeśli ![]() jest różniczkowalna w punkcie
jest różniczkowalna w punkcie ![]() , to mamy następującą równoważność:
, to mamy następującą równoważność:
![]() jest rozwiązaniem (4.1) wtw, gdy
jest rozwiązaniem (4.1) wtw, gdy ![]() dla każdego
dla każdego ![]() .
.
Uwaga 4.1
W sformułowaniu powyższego twierdzenia, jak i w wielu miejscach w dalszej części tych notatek, zastosowany jest następujący skrót myślowy. Aby mówić o różniczkowalności funkcji ![]() w punkcie
w punkcie ![]() , musi być ona określona w pewnym otoczeniu
, musi być ona określona w pewnym otoczeniu ![]() , czyli w kuli
, czyli w kuli ![]() dla pewnego
dla pewnego ![]() . Jeśli
. Jeśli ![]() jest na brzegu
jest na brzegu ![]() , to zakładać będziemy, że
, to zakładać będziemy, że ![]() jest określona na
jest określona na ![]() mimo, że jest to pominięte, dla prostoty notacji, w założeniach twierdzenia.
mimo, że jest to pominięte, dla prostoty notacji, w założeniach twierdzenia.
Uwaga 4.2
Jeśli ![]() , to warunek powyższy sprowadza się do warunku zerowania się pochodnej
, to warunek powyższy sprowadza się do warunku zerowania się pochodnej ![]() .
.
Dowód tw. 4.2
Załóżmy, że ![]() dla każdego
dla każdego ![]() . Ustalmy
. Ustalmy ![]() . Na mocy twierdzenia 3.8
. Na mocy twierdzenia 3.8
Z założenia, drugi składnik jest nieujemny, co pociąga ![]() . Z dowolności
. Z dowolności ![]() dostajemy tezę.
dostajemy tezę.
Załóżmy teraz, że ![]() jest rozwiązaniem (4.1). Ustalmy
jest rozwiązaniem (4.1). Ustalmy ![]() . Zauważmy, że wypukłość
. Zauważmy, że wypukłość ![]() implikuje
implikuje ![]() dla
dla ![]() . Z definicji pochodnej mamy
. Z definicji pochodnej mamy
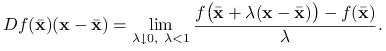 |
Ponieważ w punkcie ![]() jest minimum, to
jest minimum, to ![]() . Stąd
. Stąd ![]() .
.
Z dowodu powyższego twierdzenia dostajemy użyteczny wniosek.
Wniosek 4.1
Jeśli ![]() , gdzie
, gdzie ![]() jest wypukły, jest rozwiązaniem lokalnym (4.1) dla funkcji
jest wypukły, jest rozwiązaniem lokalnym (4.1) dla funkcji ![]() (niekoniecznie wypukłej) różniczkowalnej w
(niekoniecznie wypukłej) różniczkowalnej w ![]() , to
, to ![]() dla każdego
dla każdego ![]() .
.
Przykład 4.1
Rozważmy problem minimalizacyjny:
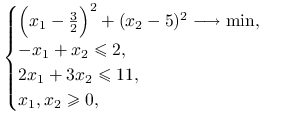 |
Zbiór ![]() zadany jest przez ograniczenia liniowe (patrz rysunek 4.1):
zadany jest przez ograniczenia liniowe (patrz rysunek 4.1):
Łatwo sprawdzić, że jest on wypukły. Funkcja ![]() jest ściśle wypukła: jej hesjan wynosi
jest ściśle wypukła: jej hesjan wynosi
Na mocy tw. 4.1 minimum jest jednoznaczne. Policzmy gradient ![]() :
:
Gradient zeruje się w punkcie ![]() , który jest poza zbiorem
, który jest poza zbiorem ![]() . Minimum należy zatem szukać na brzegu
. Minimum należy zatem szukać na brzegu ![]() . Nie mamy jeszcze narzędzi ułatwiających znalezienie tego punktu. Zgadujemy… Sprawdźmy wierzchołek
. Nie mamy jeszcze narzędzi ułatwiających znalezienie tego punktu. Zgadujemy… Sprawdźmy wierzchołek ![]() . Gradient w tym punkcie wynosi
. Gradient w tym punkcie wynosi ![]() . Zauważmy, że wektory
. Zauważmy, że wektory ![]() są kombinacjami liniowymi dodatnimi wektorów
są kombinacjami liniowymi dodatnimi wektorów ![]() i
i ![]() , tzn.
, tzn. ![]() dla pewnych
dla pewnych ![]() . Wystarczy zatem sprawdzić, że
. Wystarczy zatem sprawdzić, że ![]() i
i ![]() :
:
Na mocy tw. 4.2 minimum jest rzeczywiście w punkcie ![]() .
.
Rozszerzymy teraz twierdzenie 4.2 na klasę funkcji wypukłych nieróżniczkowalnych – skorzystamy z wprowadzonego w poprzednim rozdziale pojęcia subróżniczki.
Twierdzenie 4.3
Niech ![]() wypukły otwarty,
wypukły otwarty, ![]() wypukła. Załóżmy, że zbiór punktów dopuszczalnych
wypukła. Załóżmy, że zbiór punktów dopuszczalnych ![]() jest wypukłym podzbiorem
jest wypukłym podzbiorem ![]() . Mamy następującą równoważność:
. Mamy następującą równoważność:
![]() jest rozwiązaniem (4.1) wtw, gdy istnieje
jest rozwiązaniem (4.1) wtw, gdy istnieje ![]() , takie że
, takie że ![]() dla każdego
dla każdego ![]() .
.
Wniosek 4.2
Niech ![]() wypukły otwarty,
wypukły otwarty, ![]() wypukła. Wówczas
wypukła. Wówczas ![]() ma w
ma w ![]() minimum globalne wtw, gdy
minimum globalne wtw, gdy ![]() .
.
Dowód twierdzenia 4.3
Zacznijmy od łatwiejszej implikacji. Załóżmy, że istnieje ![]() , takie że
, takie że ![]() dla każdego
dla każdego ![]() . Z faktu, że
. Z faktu, że ![]() jest subgradientem wynika, że
jest subgradientem wynika, że
Wystarczy teraz skorzystać z założenia, żeby zauważyć, że ![]() dla
dla ![]() , czyli
, czyli ![]() jest rozwiązaniem (4.1).
jest rozwiązaniem (4.1).
Załóżmy teraz, że ![]() jest rozwiązaniem (4.1). Zdefiniujmy dwa zbiory
jest rozwiązaniem (4.1). Zdefiniujmy dwa zbiory
Oba zbiory są wypukłe, ![]() ma niepuste wnętrze (zbiór
ma niepuste wnętrze (zbiór ![]() ma puste wnętrze, jeśli
ma puste wnętrze, jeśli ![]() ma puste wnętrze). Z faktu, że punkt
ma puste wnętrze). Z faktu, że punkt ![]() jest rozwiązaniem (4.1) wynika, że
jest rozwiązaniem (4.1) wynika, że ![]() . Stosujemy słabe twierdzenie o oddzielaniu: istnieje niezerowy wektor
. Stosujemy słabe twierdzenie o oddzielaniu: istnieje niezerowy wektor ![]() i stała
i stała ![]() , takie że
, takie że
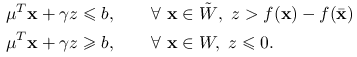 |
(4.2) |
Zanim przejdziemy do analitycznych rozważań popatrzmy na geometryczny obraz. Zauważmy, że zbiory ![]() i
i ![]() ,,stykają” się w punkcie
,,stykają” się w punkcie ![]() . Hiperpłaszczyzna oddzielająca te zbiory musi zatem przechodzić przez ten punkt. Jest ona styczna do wykresu funkcji
. Hiperpłaszczyzna oddzielająca te zbiory musi zatem przechodzić przez ten punkt. Jest ona styczna do wykresu funkcji ![]() – pierwsza grupa współrzędnych
– pierwsza grupa współrzędnych ![]() wektora
wektora ![]() do niej normalnego, z dokładnością do długości i zwrotu, wyznacza subgradient tego odwzorowania w punkcie
do niej normalnego, z dokładnością do długości i zwrotu, wyznacza subgradient tego odwzorowania w punkcie ![]() (a zatem także subgradient
(a zatem także subgradient ![]() ). Z faktu, że ta hiperpłaszczyzna jest również styczna do
). Z faktu, że ta hiperpłaszczyzna jest również styczna do ![]() dostajemy
dostajemy ![]() .
.
Udowodnijmy to teraz analitycznie. Odejmijmy od obu stron nierówności (4.2) ![]() :
:
| (4.3) | ||||
| (4.4) |
gdzie ![]() . Zauważmy najpierw, że
. Zauważmy najpierw, że ![]() nie może być większa od zera. Wówczas, wykorzystując dowolność
nie może być większa od zera. Wówczas, wykorzystując dowolność ![]() , dostajemy sprzeczność z (4.4). Kładąc w (4.4)
, dostajemy sprzeczność z (4.4). Kładąc w (4.4) ![]() i
i ![]() , otrzymujemy
, otrzymujemy ![]() . Wnioskujemy stąd, że niedopuszczalne jest
. Wnioskujemy stąd, że niedopuszczalne jest ![]() : z nierówności (4.3) (pamiętając o otwartości
: z nierówności (4.3) (pamiętając o otwartości ![]() ) dostalibyśmy bowiem
) dostalibyśmy bowiem ![]() , co przeczyłoby niezerowości wektora
, co przeczyłoby niezerowości wektora ![]() . Wykazaliśmy więc, że
. Wykazaliśmy więc, że
Biorąc ![]() , nierówność (4.3) upraszcza się do
, nierówność (4.3) upraszcza się do ![]() dla
dla ![]() . Stąd
. Stąd ![]() . Łącząc to z poprzednio otrzymaną nierównością
. Łącząc to z poprzednio otrzymaną nierównością ![]() dostajemy
dostajemy
Przechodząc w (4.3) z ![]() do
do ![]() mamy
mamy
Dzieląc obie strony przez ![]() i pamiętając, że
i pamiętając, że ![]() dostajemy
dostajemy
co dowodzi, że ![]() . Kładąc
. Kładąc ![]() w (4.4) otrzymujemy
w (4.4) otrzymujemy ![]() . Dzielimy obie strony przez
. Dzielimy obie strony przez ![]() :
:
co kończy dowód.
∎4.2. Funkcje pseudowypukłe
W tym podrozdziale wprowadzimy rodzinę funkcji, dla której spełniony jest warunek:
Okazuje się, że rodzina ta obejmuje nie tylko funkcje wypukłe.
Definicja 4.1
Niech ![]() będzie otwarty i niepusty, zaś
będzie otwarty i niepusty, zaś ![]() – różniczkowalna w
– różniczkowalna w ![]() . Funkcja
. Funkcja ![]() jest pseudowypukła w
jest pseudowypukła w ![]() , jeśli
, jeśli
Funkcja ![]() jest ściśle pseudowypukła w
jest ściśle pseudowypukła w ![]() , jeśli
, jeśli
Funkcja ![]() jest (ściśle) pseudowypukła, jeśli jest ona (ściśle) pseudowypukła w każdym punkcie
jest (ściśle) pseudowypukła, jeśli jest ona (ściśle) pseudowypukła w każdym punkcie ![]() .
.
Funkcja ![]() jest (ściśle) pseudowklęsła, jeśli
jest (ściśle) pseudowklęsła, jeśli ![]() jest (ściśle) pseudowypukła.
jest (ściśle) pseudowypukła.
Uwaga 4.3
Implikacja w definicji pseudowypukłości ma równoważną postać:
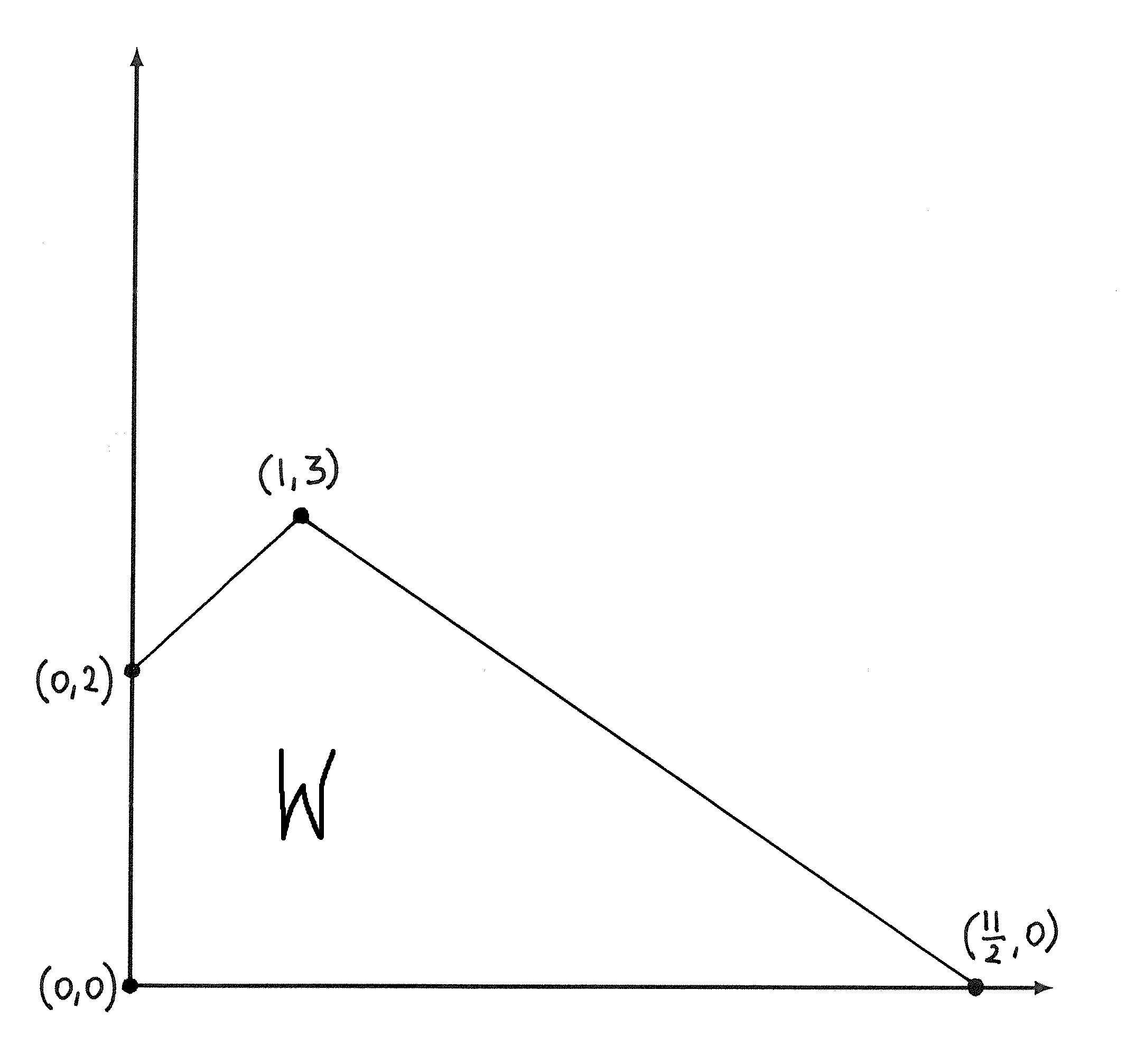
Na rysunku 4.2 znajdują się przykłady jednowymiarowych funkcji pseudowypukłych i pseudowklęsłych.
Lemat 4.1
Niech ![]() , gdzie
, gdzie ![]() wypukły, otwarty i niepusty. Jeśli
wypukły, otwarty i niepusty. Jeśli ![]() jest (ściśle) wypukła i różniczkowalna na
jest (ściśle) wypukła i różniczkowalna na ![]() , to
, to ![]() jest (ściśle) pseudowypukła.
jest (ściśle) pseudowypukła.
Dowód
Załóżmy, że ![]() wypukła. Na mocy tw. 3.8 dla dowolnych
wypukła. Na mocy tw. 3.8 dla dowolnych ![]() mamy
mamy
Jeśli zatem ![]() , to
, to ![]() i
i ![]() jest pseudowypukła. W analogiczny sposób dowodzimy, że ścisła wypukłość pociąga ścisłą pseudowypukłość.
jest pseudowypukła. W analogiczny sposób dowodzimy, że ścisła wypukłość pociąga ścisłą pseudowypukłość.
Lemat 4.2
Niech ![]() , gdzie
, gdzie ![]() , otwarty, niepusty, będzie funkcją pseudowypukłą w
, otwarty, niepusty, będzie funkcją pseudowypukłą w ![]() . Wówczas
. Wówczas ![]() jest minimum globalnym wtw, gdy
jest minimum globalnym wtw, gdy ![]() .
.
Dowód
Identyczny jak dowód wniosku 3.2.
∎Dowód poniższego lematu jest identyczny jak dowód twierdzenia 4.2.
Lemat 4.3
Niech ![]() wypukły,
wypukły, ![]() pseudowypukła. Mamy następującą równoważność:
pseudowypukła. Mamy następującą równoważność:
![]() jest rozwiązaniem (4.1) wtw, gdy
jest rozwiązaniem (4.1) wtw, gdy ![]() dla każdego
dla każdego ![]() .
.
4.3. Maksymalizacja funkcji wypukłej
Definicja 4.2
Punktem ekstremalnym zbioru wypukłego ![]() nazwiemy taki punkt
nazwiemy taki punkt ![]() , który nie jest punktem wewnętrznym żadnego odcinka zawartego w
, który nie jest punktem wewnętrznym żadnego odcinka zawartego w ![]() , tj. jeśli
, tj. jeśli ![]() dla pewnych
dla pewnych ![]() i
i ![]() , to
, to ![]() .
.
Definicja 4.3
Otoczką wypukłą punktów ![]() nazywamy zbiór punktów będących kombinacją wypukłą skończonej liczby spośród punktów
nazywamy zbiór punktów będących kombinacją wypukłą skończonej liczby spośród punktów ![]() .
.
Otoczkę wypukłą można równoważnie definiować jako najmniejszy zbiór wypukły zawierający punkty ![]() .
.
Przedstawimy teraz prostą wersję twierdzenia Kreina-Milmana.
Twierdzenie 4.4
Niech ![]() będzie zbiorem wypukłym i zwartym. Jest on wówczas otoczką wypukłą swoich punktów ekstremalnych.
będzie zbiorem wypukłym i zwartym. Jest on wówczas otoczką wypukłą swoich punktów ekstremalnych.
Przed przejściem do dowodu powyższego twierdzenia wprowadzimy niezbędne pojęcia. Przypomnijmy, że przestrzenią afiniczną nazywamy zbiór ![]() , taki że
, taki że ![]() dla dowolnych
dla dowolnych ![]() i
i ![]() takich że
takich że ![]() . Każda podprzestrzeń afiniczna
. Każda podprzestrzeń afiniczna ![]() może zostać przesunięta tak, aby zawierała
może zostać przesunięta tak, aby zawierała ![]() . Staje się ona wówczas podprzestrzenią liniową. Wymiarem podprzestrzeni afinicznej nazywamy wymiar związanej z nią podprzestrzeni liniowej.
. Staje się ona wówczas podprzestrzenią liniową. Wymiarem podprzestrzeni afinicznej nazywamy wymiar związanej z nią podprzestrzeni liniowej.
Definicja 4.4
Wymiarem zbioru wypukłego ![]() nazywamy wymiar otoczki afinicznej
nazywamy wymiar otoczki afinicznej ![]() , tzn. podprzestrzeni afinicznej generowanej przez U:
, tzn. podprzestrzeni afinicznej generowanej przez U:
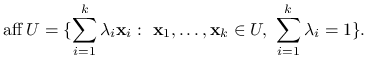 |
Zapiszmy łatwe wnioski z powyższej definicji i rozważań ją poprzedzających:
Wniosek 4.3
![]()
Zbiór wypukły o wymiarze
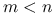 możemy traktować jako podzbiór przestrzeni
możemy traktować jako podzbiór przestrzeni 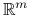 .
.Zbiór wypukły w przestrzeni
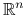 ma niepuste wnętrze wtw, gdy jego wymiar wynosi
ma niepuste wnętrze wtw, gdy jego wymiar wynosi 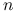 .
.
Dotychczas rozważaliśmy hiperpłaszczyzny podpierające epigraf funkcji wypukłej. Teraz uogólnimy to pojęcie na dowolny zbiór wypukły.
Lemat 4.4
Niech ![]() będzie zbiorem wypukłym o niepustym wnętrzu. Przez punkt brzegowy
będzie zbiorem wypukłym o niepustym wnętrzu. Przez punkt brzegowy ![]() przechodzi wówczas hiperpłaszczyzna, taka że zbiór
przechodzi wówczas hiperpłaszczyzna, taka że zbiór ![]() leży w jednej z wyznaczonych przez nią półprzestrzeni. Hiperpłaszczyznę tą nazywamy hiperpłaszczyzną podpierającą zbiór
leży w jednej z wyznaczonych przez nią półprzestrzeni. Hiperpłaszczyznę tą nazywamy hiperpłaszczyzną podpierającą zbiór ![]() w punkcie
w punkcie ![]() .
.
Dowód
Na mocy słabego twierdzenia o oddzielaniu zastosowanego do ![]() i
i ![]() (zauważmy, że
(zauważmy, że ![]() ) istnieje
) istnieje ![]() , takie że
, takie że ![]() dla każdego
dla każdego ![]() . Szukaną hiperpłaszczyzną jest
. Szukaną hiperpłaszczyzną jest
Zbiór ![]() zawarty jest w półprzestrzeni
zawarty jest w półprzestrzeni ![]() .
.
Dowód twierdzenia 4.4
Przeprowadzimy indukcję po wymiarze ![]() zbioru zwartego i wypukłego
zbioru zwartego i wypukłego ![]() . Przypadki
. Przypadki ![]() (
(![]() jest punktem) i
jest punktem) i ![]() (
(![]() jest odcinkiem) są trywialne. Czas na krok indukcyjny. Załóżmy, że każdy zbiór wypukły i zwarty o wymiarze nie większym od
jest odcinkiem) są trywialne. Czas na krok indukcyjny. Załóżmy, że każdy zbiór wypukły i zwarty o wymiarze nie większym od ![]() jest otoczką wypukłą swoich punktów ekstremalnych. Weźmy zbiór wypukły i zwarty
jest otoczką wypukłą swoich punktów ekstremalnych. Weźmy zbiór wypukły i zwarty ![]() o wymiarze
o wymiarze ![]() . Zbiór ten traktujemy jako podzbiór
. Zbiór ten traktujemy jako podzbiór ![]() . Ma on wówczas niepuste wnętrze. Niech
. Ma on wówczas niepuste wnętrze. Niech ![]() .
.
Przypadek (I): ![]() leży na brzegu
leży na brzegu ![]() . Na mocy lematu 4.4 istnieje hiperpłaszczyzna podpierająca
. Na mocy lematu 4.4 istnieje hiperpłaszczyzna podpierająca ![]() przechodząca przez
przechodząca przez ![]() . Zbiór
. Zbiór ![]() jest wypukły, zwarty i o wymiarze co najwyżej
jest wypukły, zwarty i o wymiarze co najwyżej ![]() . Na mocy założenia indukcyjnego punkt
. Na mocy założenia indukcyjnego punkt ![]() jest kombinacją wypukłą punktów ekstremalnych
jest kombinacją wypukłą punktów ekstremalnych ![]() . Pozostaje już tylko wykazać, że punkty ekstremalne
. Pozostaje już tylko wykazać, że punkty ekstremalne ![]() są punktami ekstremalnymi
są punktami ekstremalnymi ![]() . Wynika to stąd, że żaden punkt
. Wynika to stąd, że żaden punkt ![]() nie może być przedstawiony jako kombinacja wypukła punktów, z których jeden lub oba nie należą do
nie może być przedstawiony jako kombinacja wypukła punktów, z których jeden lub oba nie należą do ![]() .
.
Przypadek (II): ![]() leży we wnętrzu
leży we wnętrzu ![]() . Przeprowadźmy przez
. Przeprowadźmy przez ![]() dowolną prostą. Przecina ona brzeg
dowolną prostą. Przecina ona brzeg ![]() w dwóch punktach
w dwóch punktach ![]() . Z przypadku (I) wiemy, że każdy z punktów
. Z przypadku (I) wiemy, że każdy z punktów ![]() może zostać przedstawiony jako kombinacja wypukła skończonej liczby punktów ekstremalnych
może zostać przedstawiony jako kombinacja wypukła skończonej liczby punktów ekstremalnych ![]() . Punkt
. Punkt ![]() może być zapisany jako kombinacja wypukła
może być zapisany jako kombinacja wypukła ![]() , a więc należy do otoczki wypukłej punktów ekstremalnych
, a więc należy do otoczki wypukłej punktów ekstremalnych ![]() .
.
Poniżej prezentujemy inny dowód twierdzenia 4.4 bazujący częściowo na pomysłach wykorzystywanych w dowodzie ogólnej wersji twierdzenia Kreina-Milmana. W przeciwieństwie do powyższego rozumowania, dowód ten nie jest konstruktywny.
Alternatywny dowód twierdzenia 4.4
Jeśli zbiór ![]() zawarty jest w
zawarty jest w ![]() , to teza twierdzenia jest trywialna. Załóżmy więc, że każdy wypukły zwarty podzbiór
, to teza twierdzenia jest trywialna. Załóżmy więc, że każdy wypukły zwarty podzbiór ![]() jest otoczką wypukłą swoich punktów ekstremalnych. Udowodnimy prawdziwość tego stwierdzenia dla
jest otoczką wypukłą swoich punktów ekstremalnych. Udowodnimy prawdziwość tego stwierdzenia dla ![]() . Niech
. Niech ![]() będzie otoczką wypukłą punktów ekstremalnych
będzie otoczką wypukłą punktów ekstremalnych ![]() . Oczywiście
. Oczywiście ![]() . Przypuśćmy, że istnieje
. Przypuśćmy, że istnieje ![]() . Wówczas możemy znaleźć kulę o środku w
. Wówczas możemy znaleźć kulę o środku w ![]() i dostatecznie małym promieniu, która nie przecina
i dostatecznie małym promieniu, która nie przecina ![]() . Na mocy mocnego twierdzenia o oddzielaniu, tw. 3.2, istnieje wektor
. Na mocy mocnego twierdzenia o oddzielaniu, tw. 3.2, istnieje wektor ![]() , taki że
, taki że ![]() dla
dla ![]() i
i ![]() . Niech
. Niech ![]() . Supremum to jest po całym zbiorze
. Supremum to jest po całym zbiorze ![]() i jest skończone ze zwartości
i jest skończone ze zwartości ![]() . Hiperpłaszczyzna
. Hiperpłaszczyzna ![]() nie przecina
nie przecina ![]() (bo
(bo ![]() ), ale ma punkt wspólny z
), ale ma punkt wspólny z ![]() . Rzeczywiście,
. Rzeczywiście, ![]() jest niepusty, gdyż ze zwartości
jest niepusty, gdyż ze zwartości ![]() wynika, że supremum definiujące
wynika, że supremum definiujące ![]() jest osiągane, czyli istnieje
jest osiągane, czyli istnieje ![]() , dla którego
, dla którego ![]() . Pokażemy, że
. Pokażemy, że ![]() zawiera punkt ekstremalny
zawiera punkt ekstremalny ![]() , co będzie sprzeczne z definicją zbioru
, co będzie sprzeczne z definicją zbioru ![]() . Zbiór
. Zbiór ![]() jest niepustym, zwartym zbiorem wypukłym w przestrzeni afinicznej o wymiarze
jest niepustym, zwartym zbiorem wypukłym w przestrzeni afinicznej o wymiarze ![]() . Zbiór
. Zbiór ![]() możemy traktować jako podzbiór
możemy traktować jako podzbiór ![]() , czyli na mocy założenia indukcyjnego jest on otoczką wypukłą swoich punktów ekstremalnych. Niech
, czyli na mocy założenia indukcyjnego jest on otoczką wypukłą swoich punktów ekstremalnych. Niech ![]() będzie jednym z punktów ekstremalnych
będzie jednym z punktów ekstremalnych ![]() i załóżmy, że jest on kombinacją wypukłą
i załóżmy, że jest on kombinacją wypukłą ![]() ,
, ![]() dla
dla ![]() . Wówczas
. Wówczas ![]() . Z konstrukcji
. Z konstrukcji ![]() wynika, że zarówno
wynika, że zarówno ![]() jak i
jak i ![]() muszą być równe
muszą być równe ![]() , czyli
, czyli ![]() . Z faktu, że
. Z faktu, że ![]() jest punktem ekstremalnym
jest punktem ekstremalnym ![]() wnioskujemy, że
wnioskujemy, że ![]() , czyli
, czyli ![]() jest punktem ekstremalnym
jest punktem ekstremalnym ![]() .
.
Twierdzenie 4.5
Niech ![]() wypukła, ciągła, określona na wypukłym i zwartym zbiorze
wypukła, ciągła, określona na wypukłym i zwartym zbiorze ![]() . Wówczas punkt ekstremalny zbioru
. Wówczas punkt ekstremalny zbioru ![]() jest jednym z rozwiązań globalnych problemu
jest jednym z rozwiązań globalnych problemu
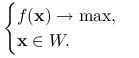 |
Dowód
Funkcja ciągła osiąga swoje kresy na zbiorze zwartym. Powyższy problem maksymalizacyjny ma zatem rozwiązanie ![]() . Na mocy tw. 4.4 punkt
. Na mocy tw. 4.4 punkt ![]() jest kombinacją wypukłą skończonej liczby punktów ekstremalnych,
jest kombinacją wypukłą skończonej liczby punktów ekstremalnych, ![]() , zbioru
, zbioru ![]() , tzn.
, tzn.
dla liczb ![]() takich że
takich że ![]() . Z wypukłości
. Z wypukłości ![]() dostajemy
dostajemy
Z faktu, że ![]() jest maksimum
jest maksimum ![]() na zbiorze
na zbiorze ![]() wynika, że
wynika, że ![]() .
.
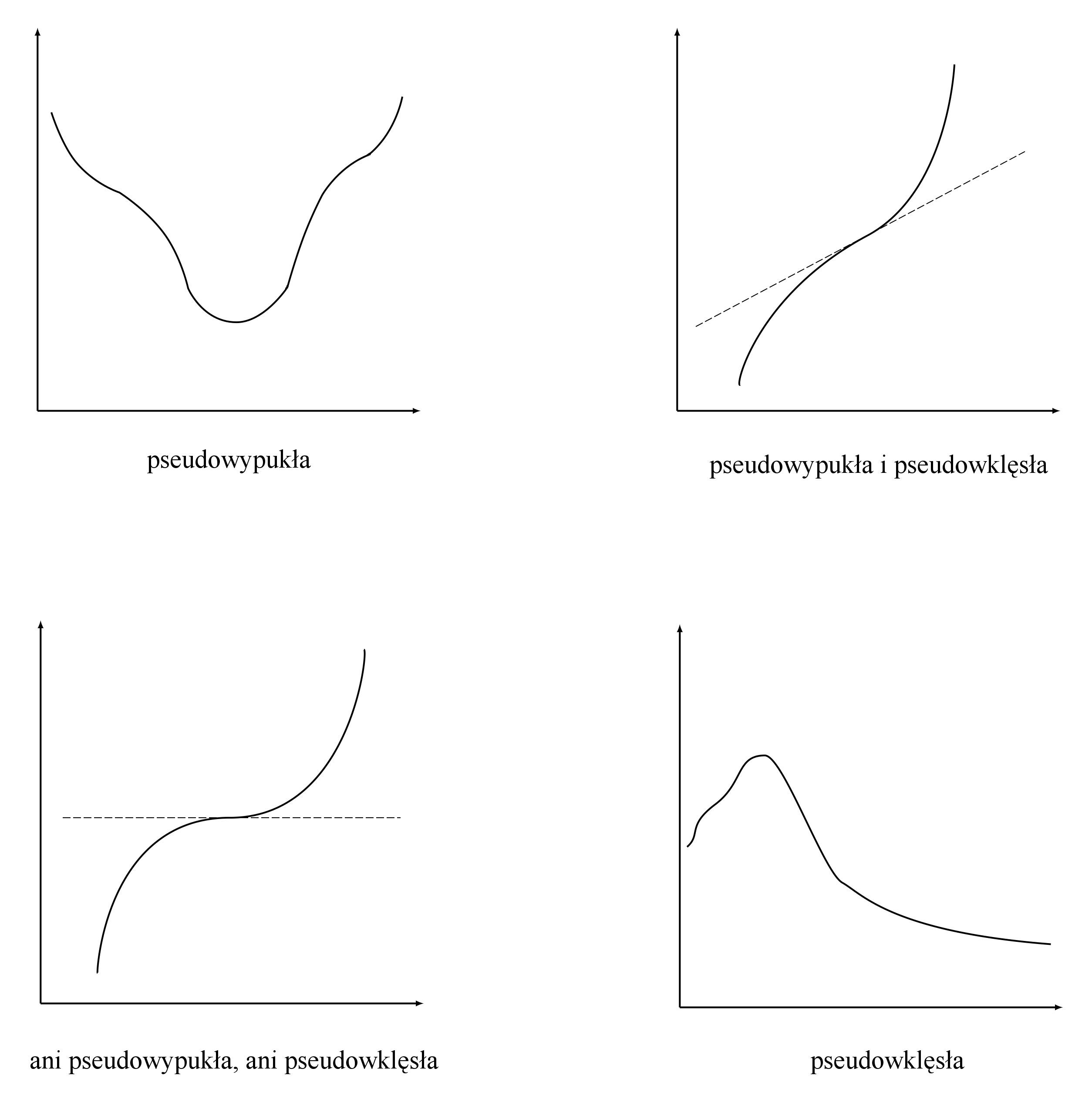
Przykład 4.2
Rozważmy następujące zadanie optymalizacyjne:
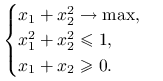 |
Funkcja celu jest wypukła, więc na mocy twierdzenia 4.5 punkt ekstremalny jest rozwiązaniem. Zbiór punktów dopuszczalnych jest kołem przeciętym z półprzestrzenią, czyli zbiorem wypukłym. Zbiór punktów ekstremalnych zaznaczony jest pogrubioną linią na rysunku 4.3. Jest to fragment okręgu. Zmaksymalizujmy więc funkcję celu na całym okręgu i zobaczmy, czy rozwiązanie należy do tego fragmentu okręgu. Podstawiając ![]() do funkcji celu dostajemy
do funkcji celu dostajemy
Rozwiązaniem tego problemu jest ![]() Stąd
Stąd ![]() Para
Para ![]() należy do półokręgu punktów ekstremalnych, więc jest rozwiązaniem, lecz niekoniecznie jedynym. Para
należy do półokręgu punktów ekstremalnych, więc jest rozwiązaniem, lecz niekoniecznie jedynym. Para ![]() nie należy do zbioru punktów dopuszczalnych.
nie należy do zbioru punktów dopuszczalnych.
Twierdzenie 4.5 jest szczególnie użyteczne przy maksymalizacji funkcji wypukłej na zbiorach wielościennych:
Definicja 4.5
Zbiór ![]() nazwiemy zbiorem wielościennym, jeśli jest przecięciem skończonej rodziny półprzestrzeni, tzn.
nazwiemy zbiorem wielościennym, jeśli jest przecięciem skończonej rodziny półprzestrzeni, tzn.
gdzie ![]() ,
, ![]() i
i ![]() .
.
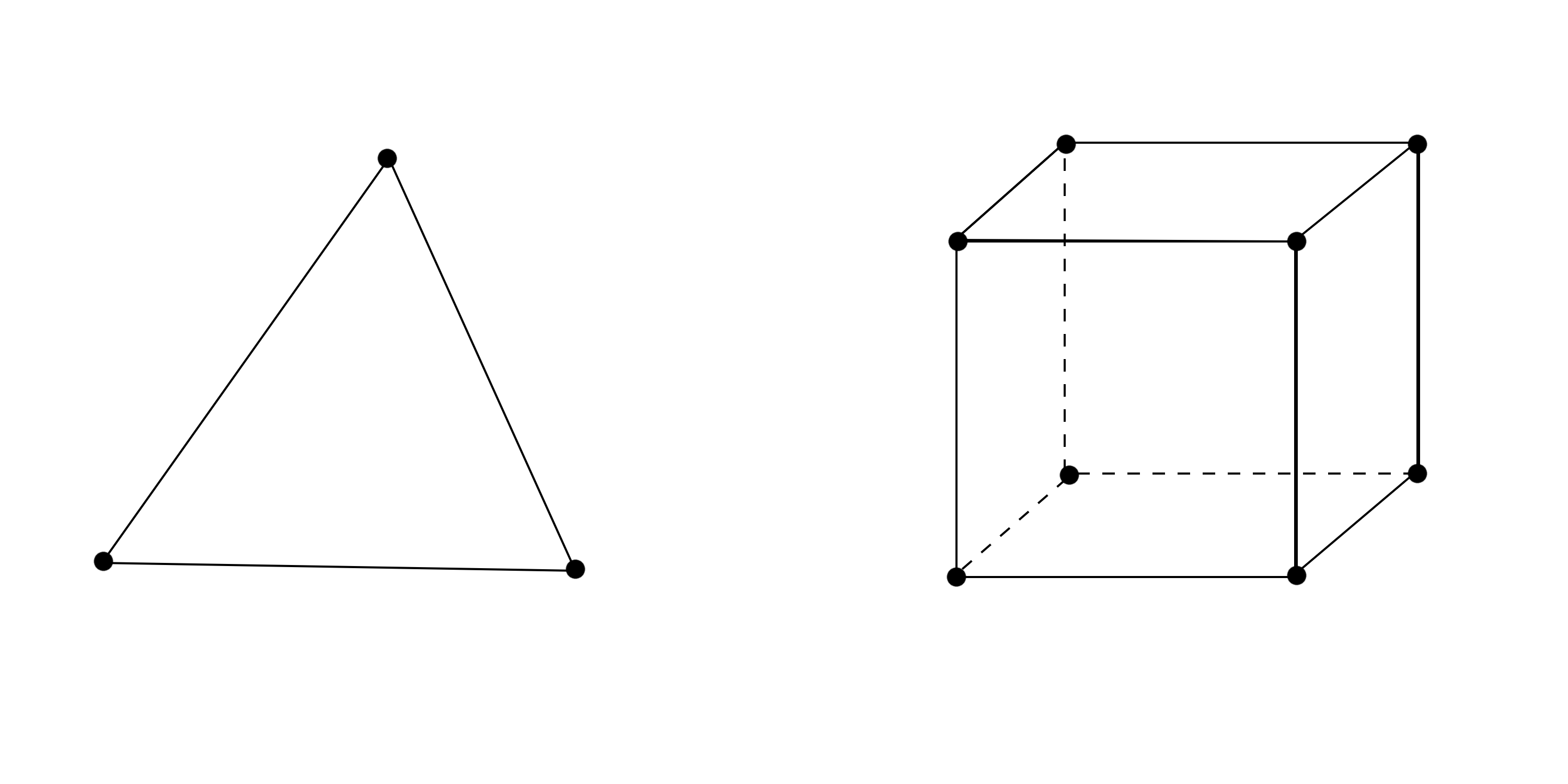
Łatwo można zauważyć, że punktami ekstremalnymi ograniczonych zbiorów wielościennych są ,,wierzchołki” (patrz rys. 4.4).
Lemat 4.5
Zbiór wielościenny jest domknięty i wypukły.
Dowód
Zbiór wielościenny jest domknięty i wypukły jako przecięcie rodziny zbiorów domkniętych i wypukłych.
∎Przykład 4.3
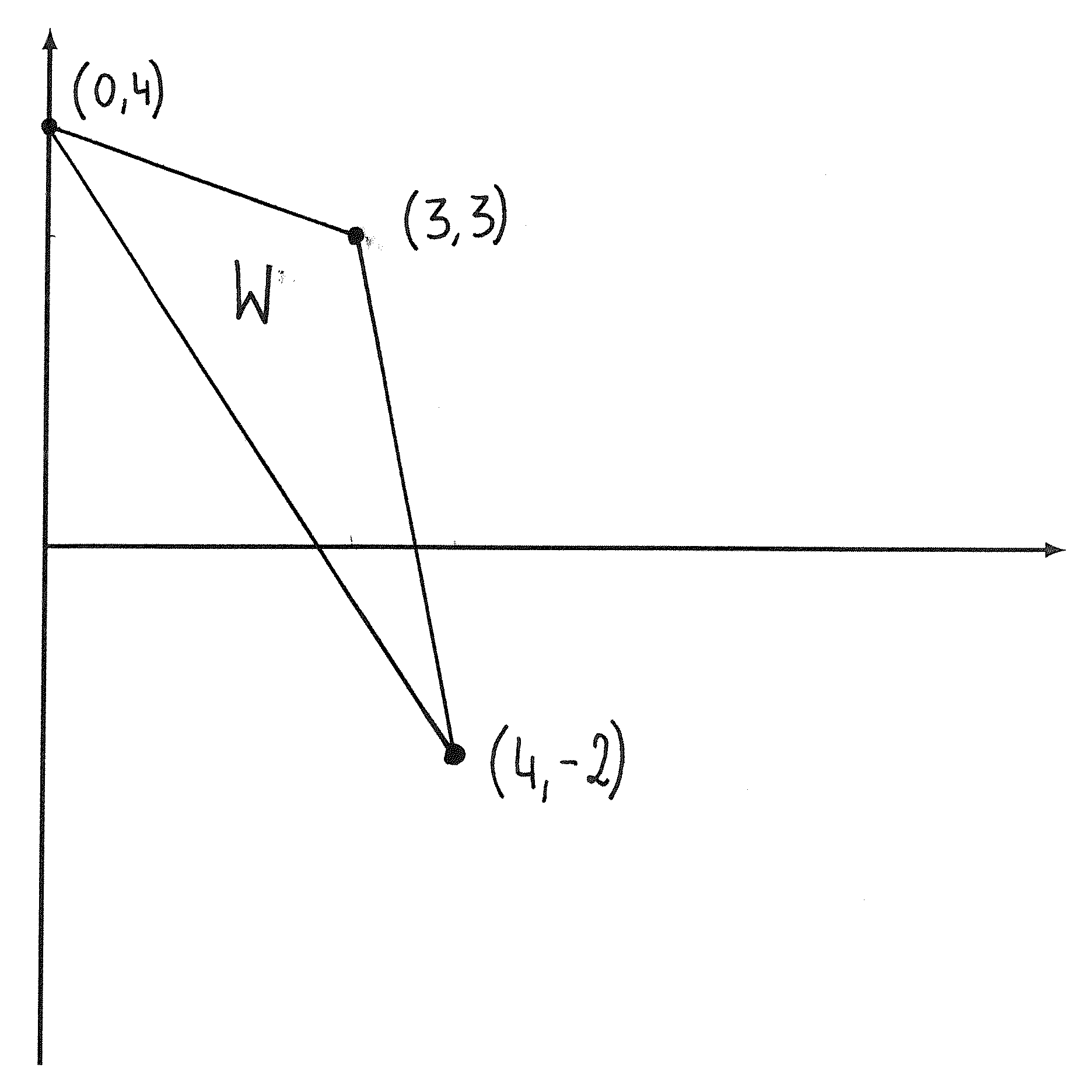
Rozważmy problem optymalizacyjny
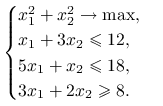 |
Funkcja celu jest wypukła, zaś zbiór punktów dopuszczalnych jest wielościenny. Jego punkty ekstremalne to ![]() ,
, ![]() i
i ![]() , patrz rysunek 4.5. Wartość funkcji celu w tych punktach wynosi odpowiednio:
, patrz rysunek 4.5. Wartość funkcji celu w tych punktach wynosi odpowiednio: ![]() ,
, ![]() i
i ![]() . Rozwiązaniem jest zatem punkt
. Rozwiązaniem jest zatem punkt ![]() . Można łatwo dowieść, że jest to jedyne rozwiązanie tego problemu.
. Można łatwo dowieść, że jest to jedyne rozwiązanie tego problemu.
4.4. Zadania
Ćwiczenie 4.1
Udowodnij, że zbiór rozwiązań globalnych zagadnienia (4.1) jest wypukły dla wypukłego zbioru ![]() i wypukłej funkcji
i wypukłej funkcji ![]() .
.
Ćwiczenie 4.2
Rozważmy zagadnienie (4.1) dla wypukłego zbioru ![]() i wypukłej funkcji
i wypukłej funkcji ![]() . Wykaż, że ścisłe rozwiązanie lokalne jest jedynym rozwiązaniem globalnym.
. Wykaż, że ścisłe rozwiązanie lokalne jest jedynym rozwiązaniem globalnym.
Ćwiczenie 4.3
Udowodnij: Niech ![]() wypukły oraz
wypukły oraz ![]() różniczkowalne. Jeśli zachodzi jeden z poniższych warunków:
różniczkowalne. Jeśli zachodzi jeden z poniższych warunków:
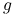 jest wypukła,
jest wypukła, 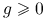 , oraz
, oraz 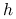 jest wklęsła,
jest wklęsła, 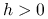 ,
,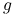 jest wypukła,
jest wypukła, 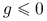 , oraz
, oraz 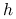 jest wypukła,
jest wypukła, 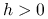 ,
,
to ![]() jest pseudowypukła. Podaj przykład, że
jest pseudowypukła. Podaj przykład, że ![]() nie jest wypukła.
nie jest wypukła.
Ćwiczenie 4.4
Udowodnij: Niech ![]() wypukły oraz
wypukły oraz ![]() różniczkowalne. Jeśli
różniczkowalne. Jeśli ![]() jest wypukła i
jest wypukła i ![]() oraz
oraz ![]() jest wklęsła,
jest wklęsła, ![]() , to
, to ![]() jest pseudowypukła.
jest pseudowypukła.
Ćwiczenie 4.5
Udowodnij, że zbiór minimów funkcji pseudowypukłej ![]() , gdzie
, gdzie ![]() wypukły, jest zbiorem wypukłym.
wypukły, jest zbiorem wypukłym.
Ćwiczenie 4.6
Odpowiedz na następujące pytania:
Czy suma funkcji pseudowypukłych jest pseudowypukła?
Czy jeśli funkcje
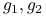 są pseudowypukłe w punkcie
są pseudowypukłe w punkcie 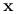 oraz
oraz 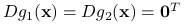 , to funkcja
, to funkcja 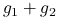 jest pseudowypukła w
jest pseudowypukła w 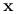 ?
?Czy suma funkcji pseudowypukłej i wypukłej jest pseudowypukła?
Odpowiedzi uzasadnij kontrprzykładami lub dowodami.
Ćwiczenie 4.8
Znaleźć rozwiązania zadania
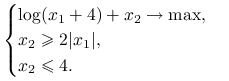 |
Skorzystaj z tw. 4.2.
Ćwiczenie 4.9
Rozwiąż zadanie
![\begin{cases}\frac{e^{{(x_{1}-3)^{2}+x_{2}}}}{\log(x_{2})}\to\min,&\\
x_{2}>1,&\\
x_{1}\in[1,100].&\end{cases}](wyklady/op2/mi/mi762.png) |
Ćwiczenie 4.10
Udowodnij, że ![]() jest punktem ekstremalnym zbioru wypukłego
jest punktem ekstremalnym zbioru wypukłego ![]() wtw, gdy
wtw, gdy ![]() jest zbiorem wypukłym.
jest zbiorem wypukłym.
Ćwiczenie 4.11
Wykaż, że jeśli w punkcie brzegowym ![]() zbioru wypukłego
zbioru wypukłego ![]() istnieje hiperpłaszczyzna podpierająca
istnieje hiperpłaszczyzna podpierająca ![]() , taka że
, taka że ![]() , to punkt
, to punkt ![]() jest punktem ekstremalnym
jest punktem ekstremalnym ![]() .
.
Ćwiczenie 4.12
Zbadaj związek pomiędzy subróżniczką funkcji wypukłej w punkcie ![]() a hiperpłaszczyznami podpierającymi epigraf tej funkcji w tym punkcie.
a hiperpłaszczyznami podpierającymi epigraf tej funkcji w tym punkcie.
Ćwiczenie 4.13
Znaleźć rozwiązanie zadania
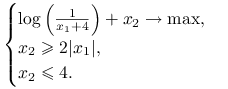 |
Ćwiczenie 4.14
Rozwiąż problem programowania nieliniowego z ograniczeniami:
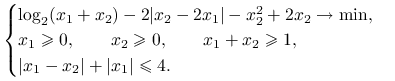 |
Ćwiczenie 4.15
([3, Zadania 3.28, 3.29])
Zdefiniujmy ![]() najstępująco:
najstępująco:
gdzie ![]() jest zbiorem wielościennym,
jest zbiorem wielościennym, ![]() ,
, ![]() .
.
Wykaż, że
 jest wklęsła.
jest wklęsła.
Scharakteryzuj subróżniczkę
 .
.Znajdź subróżniczkę w punktach
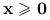 dla
dla