Zagadnienia
5. Warunek konieczny I rzędu
5.1. Stożek kierunków stycznych
Rozważmy problem optymalizacyjny
 |
(5.1) |
gdzie ![]() i
i ![]() . Niech
. Niech ![]() będzie rozwiązaniem lokalnym. Będziemy chcieli powiązać geometrię lokalną zbioru
będzie rozwiązaniem lokalnym. Będziemy chcieli powiązać geometrię lokalną zbioru ![]() w punkcie
w punkcie ![]() z zachowaniem funkcji
z zachowaniem funkcji ![]() , czyli kierunkami spadku jej wartości. Przez lokalną geometrię
, czyli kierunkami spadku jej wartości. Przez lokalną geometrię ![]() rozumiemy zbiór kierunków, w których możemy się poruszyć z punktu
rozumiemy zbiór kierunków, w których możemy się poruszyć z punktu ![]() nie opuszczając
nie opuszczając ![]() .
.
Definicja 5.1
Stożkiem kierunków stycznych ![]() do
do ![]() w punkcie
w punkcie ![]() nazywamy zbiór wektorów
nazywamy zbiór wektorów ![]() takich że
takich że
dla pewnych ![]() ,
, ![]() i
i ![]() .
.
Powyższa definicja mówi, iż kierunek ![]() należy do stożka kierunków stycznych
należy do stożka kierunków stycznych ![]() , jeśli jest on granicą kierunków wyznaczonych przez ciąg punktów dopuszczalnych
, jeśli jest on granicą kierunków wyznaczonych przez ciąg punktów dopuszczalnych ![]() zmierzających to
zmierzających to ![]() Zapisać możemy to formalnie w następujący sposób:
Zapisać możemy to formalnie w następujący sposób:
| (5.2) |
Dowód tej tożsamości oraz poniższego lematu pozostawiamy jako ćwiczenie.
Lemat 5.1
Zbiór
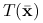 jest stożkiem, tzn.
jest stożkiem, tzn. 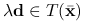 dla dowolnych
dla dowolnych 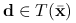 i
i 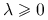 . W szczególności,
. W szczególności, 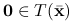 .
.Jeśli
 jest punktem wewnętrznym zbioru
jest punktem wewnętrznym zbioru 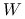 , to
, to 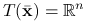 .
.Stożek
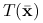 jest domknięty.
jest domknięty.
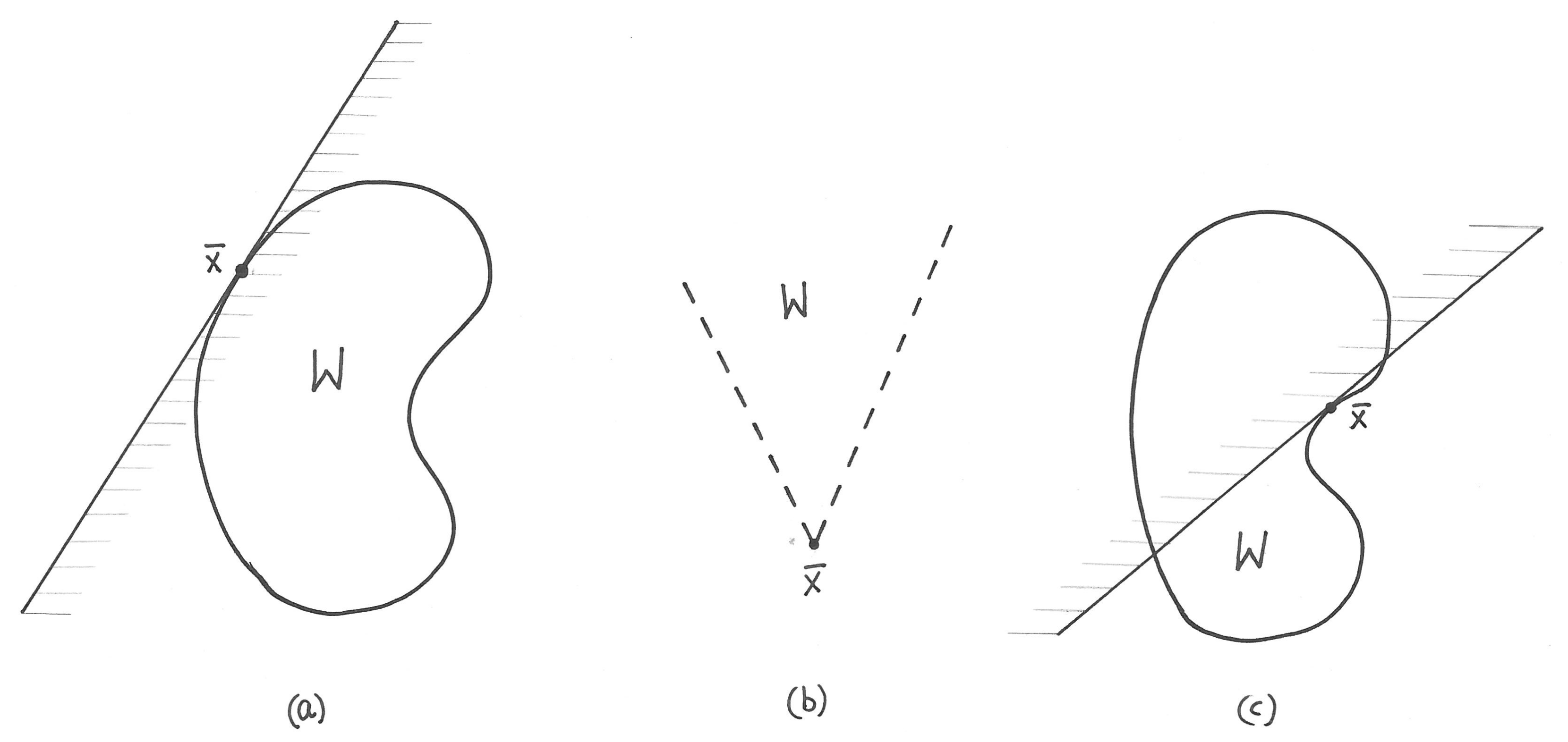
Przykład 5.1
Na rysunku 5.1 znajdują się trzy przykłady zbiorów i stożków do nich stycznych w punkcie ![]() . Stożki te są przesunięte o wektor
. Stożki te są przesunięte o wektor ![]() , by pokazać ich zależność od kształtu zbioru. W przykładzie (a) i (c) zakładamy, że brzeg zbioru
, by pokazać ich zależność od kształtu zbioru. W przykładzie (a) i (c) zakładamy, że brzeg zbioru ![]() jest gładki, więc stożki te są półprzestrzeniami ograniczonymi przez styczną w
jest gładki, więc stożki te są półprzestrzeniami ograniczonymi przez styczną w ![]() . W przykładzie (b) zbiór
. W przykładzie (b) zbiór ![]() to środek narysowanego stożka (bez brzegu). Wówczas stożek kierunków stycznych jest domknięciem zbioru
to środek narysowanego stożka (bez brzegu). Wówczas stożek kierunków stycznych jest domknięciem zbioru ![]() .
.
Jak już wspomnieliśmy, stożek kierunków stycznych jest ściśle związany z rozwiązaniem zagadnienia (5.1). Jeśli w punkcie ![]() funkcja
funkcja ![]() ma minimum lokalne na
ma minimum lokalne na ![]() , to wówczas kierunki spadku wartości funkcji
, to wówczas kierunki spadku wartości funkcji ![]() nie mogą należeć do zbioru kierunków stycznych w punkcie
nie mogą należeć do zbioru kierunków stycznych w punkcie ![]() . Gdyby tak nie było, to poruszając się w kierunku spadku funkcji
. Gdyby tak nie było, to poruszając się w kierunku spadku funkcji ![]() zmniejszalibyśmy jej wartość jednocześnie pozostając w zbiorze
zmniejszalibyśmy jej wartość jednocześnie pozostając w zbiorze ![]() . Intuicje te formalizujemy poniżej.
. Intuicje te formalizujemy poniżej.
Definicja 5.2
Niech ![]() będzie różniczkowalna w
będzie różniczkowalna w ![]() . Zbiorem kierunków spadku funkcji
. Zbiorem kierunków spadku funkcji ![]() w punkcie
w punkcie ![]() nazywamy
nazywamy
Dowód
Weźmy ![]() . Wówczas
. Wówczas ![]() dla pewnego ciągu punktów
dla pewnego ciągu punktów ![]() zbieżnego do
zbieżnego do ![]() oraz ciągu liczb
oraz ciągu liczb ![]() . Z definicji różniczkowalności
. Z definicji różniczkowalności ![]() w
w ![]() mamy
mamy
Z faktu, że ![]() jest rozwiązaniem lokalnym
jest rozwiązaniem lokalnym ![]() dla dostatecznie dużych
dla dostatecznie dużych ![]() . W połączeniu z powyższym wzorem daje to następujące oszacowanie:
. W połączeniu z powyższym wzorem daje to następujące oszacowanie:
Mnożąc obie strony powyższej nierówności przez ![]() dostajemy
dostajemy
Zrobimy teraz sztuczkę, aby rozwiązać problem z ![]() i przejdziemy z
i przejdziemy z ![]() to nieskończoności:
to nieskończoności:
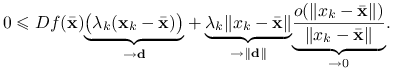 |
Udowodniliśmy zatem, że ![]() , czyli
, czyli ![]() . Kończy to dowód twierdzenia.
. Kończy to dowód twierdzenia.
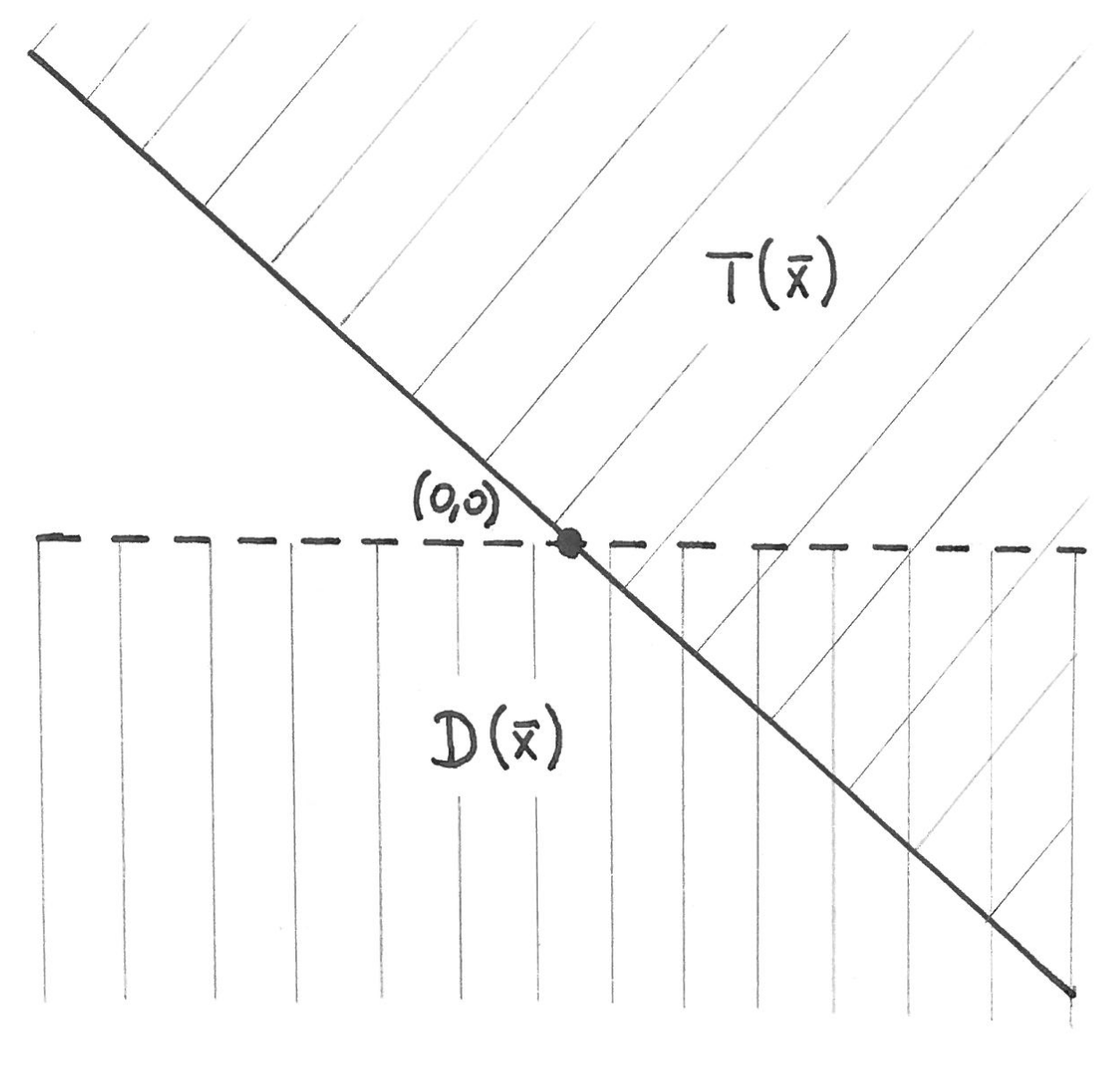
Przykład 5.2
Rozważmy następujący problem optymalizacyjny:
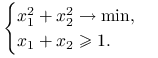 |
Oznaczmy ![]() i
i ![]() . Zbadamy zbiory
. Zbadamy zbiory ![]() i
i ![]() w następujących punktach:
w następujących punktach: ![]() .
.
![{\bar{\mathbf{x}}}=[1,1]^{T}](wyklady/op2/mi/mi988.png) . Punkt ten leży wewnątrz zbioru
. Punkt ten leży wewnątrz zbioru 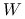 , czyli
, czyli 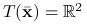 . Zbiór kierunków spadku funkcji
. Zbiór kierunków spadku funkcji  dany jest następująco:
dany jest następująco:![D({\bar{\mathbf{x}}})=\big\{\mathbf{d}\in\mathbb{R}^{2}:\ Df({\bar{\mathbf{x}}})\mathbf{d}<0\big\}=\big\{\mathbf{d}\in\mathbb{R}^{2}:\ [2,2]\mathbf{d}<0\big\}=\big\{\mathbf{d}\in\mathbb{R}^{2}:\ d_{1}+d_{2}<0\big\}.](wyklady/op2/mi/mi929.png)
W oczywisty sposób część wspólna powyższych zbiorów nie jest pusta, czyli w punkcie
![[1,1]^{T}](wyklady/op2/mi/mi909.png) nie ma minimum.
nie ma minimum.-
![{\bar{\mathbf{x}}}=[1,0]^{T}](wyklady/op2/mi/mi974.png) . Punkt ten leży na brzegu zbioru
. Punkt ten leży na brzegu zbioru 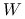 . Łatwo można zauważyć, że
. Łatwo można zauważyć, że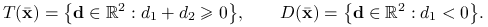
Zbiory te mają niepuste przecięcie (patrz podwójna kratka na rys. 5.2), więc w punkcie
![[1,0]^{T}](wyklady/op2/mi/mi998.png) nie ma minimum.
nie ma minimum. ![{\bar{\mathbf{x}}}=[\frac{1}{2},\frac{1}{2}]^{T}](wyklady/op2/mi/mi914.png) . Zauważmy, że
. Zauważmy, że![T({\bar{\mathbf{x}}})=\big\{\mathbf{d}\in\mathbb{R}^{2}:d_{1}+d_{2}\ge 0\big\},\qquad D({\bar{\mathbf{x}}})=\big\{\mathbf{d}\in\mathbb{R}^{2}:\ [1,1]\mathbf{d}<0\big\}=\big\{\mathbf{d}\in\mathbb{R}^{2}:d_{1}+d_{2}<0\big\}.](wyklady/op2/mi/mi923.png)
Zbiory te mają zatem puste przecięcie, więc w punkcie
![[\frac{1}{2},\frac{1}{2}]^{T}](wyklady/op2/mi/mi960.png) może być minimum.
może być minimum.
Bezpośrednie wykorzystanie twierdzenia 5.1 do szukania kandydatów na rozwiązania zadań z ograniczeniami nie wygląda zachęcająco. Dlatego postaramy się opisać prościej zbiór ![]() oraz warunek
oraz warunek ![]() .
.
5.2. Ograniczenia nierównościowe
Zajmiemy się problemem optymalizacyjnym w następującej formie:
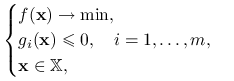 |
(5.3) |
gdzie ![]() jest zbiorem otwartym i
jest zbiorem otwartym i ![]() . A zatem
. A zatem
| (5.4) |
Funkcje ![]() nazywane są ograniczeniami nierównościowymi, zaś cały problem (5.3) zadaniem optymalizacyjnym z ograniczeniami nierównościowymi.
nazywane są ograniczeniami nierównościowymi, zaś cały problem (5.3) zadaniem optymalizacyjnym z ograniczeniami nierównościowymi.
Ustalmy ![]() i załóżmy, że funkcje
i załóżmy, że funkcje ![]() są ciągłe. Wówczas ruch wokół
są ciągłe. Wówczas ruch wokół ![]() ograniczają lokalnie tylko te warunki, dla których
ograniczają lokalnie tylko te warunki, dla których ![]() . W przypadku pozostałych, z ciągłości
. W przypadku pozostałych, z ciągłości ![]() wynika, iż istnieje pewne otoczenie
wynika, iż istnieje pewne otoczenie ![]() , na którym mamy
, na którym mamy ![]() . Okazuje się, że ta obserwacja będzie pełnić ważną rolę w procesie optymalizacji z ograniczeniami nierównościowymi.
. Okazuje się, że ta obserwacja będzie pełnić ważną rolę w procesie optymalizacji z ograniczeniami nierównościowymi.
Definicja 5.3
Zbiorem ograniczeń aktywnych w punkcie ![]() nazywamy zbiór
nazywamy zbiór
Głównym wynikiem tego rozdziału będzie powiązanie własności ograniczeń aktywnych w danym punkcie ![]() z lokalną geometrią tego zbioru wokół
z lokalną geometrią tego zbioru wokół ![]() . W tym celu wprowadźmy następującą definicję.
. W tym celu wprowadźmy następującą definicję.
Definicja 5.4
Niech ![]() i
i ![]() różniczkowalne w
różniczkowalne w ![]() dla ograniczeń aktywnych
dla ograniczeń aktywnych ![]() . Stożkiem kierunków stycznych dla ograniczeń zlinearyzowanych nazywamy zbiór
. Stożkiem kierunków stycznych dla ograniczeń zlinearyzowanych nazywamy zbiór
Stożek kierunków stycznych dla ograniczeń zlinearyzowanych jest zbiorem wielościennym, a zatem wypukłym i domkniętym.
Lemat 5.2
Jeśli ![]() , to
, to
Dowód
Dowód przebiega bardzo podobnie do dowodu twierdzenia 5.1. Weźmy ![]() . Wówczas
. Wówczas ![]() dla pewnego ciągu punktów
dla pewnego ciągu punktów ![]() zbieżnego do
zbieżnego do ![]() oraz ciągu liczb dodatnich
oraz ciągu liczb dodatnich ![]() . Ustalmy
. Ustalmy ![]() . Z definicji różniczkowalności
. Z definicji różniczkowalności ![]() w
w ![]() mamy
mamy
Ograniczenie ![]() -te jest aktywne w
-te jest aktywne w ![]() . Zatem
. Zatem ![]() . Oczywiście,
. Oczywiście, ![]() , ponieważ
, ponieważ ![]() . W połączeniu w powyższym wzorem daje to następujące oszacowanie:
. W połączeniu w powyższym wzorem daje to następujące oszacowanie:
Mnożąc obie strony powyższej nierówności przez ![]() dostajemy
dostajemy
Zrobimy teraz sztuczkę, aby rozwiązać problem ![]() i przejdziemy z
i przejdziemy z ![]() to nieskończoności:
to nieskończoności:
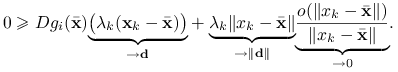 |
Udowodniliśmy zatem, że ![]() . Analogicznie wynik otrzymujemy dla każdego ograniczenia aktywnego
. Analogicznie wynik otrzymujemy dla każdego ograniczenia aktywnego ![]() . A zatem
. A zatem ![]()
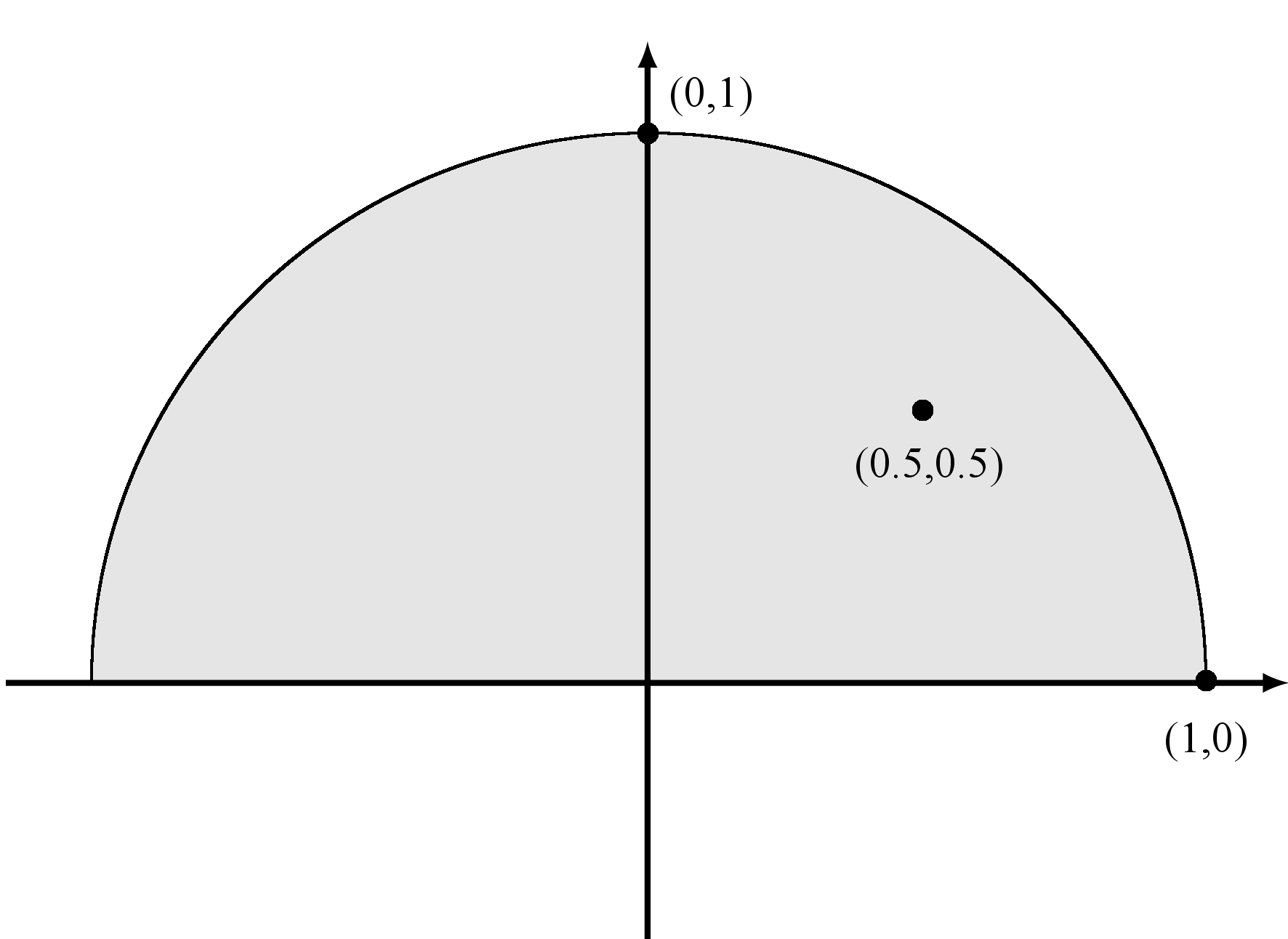
Przykład 5.3
Rozważmy zbiór ![]() , patrz rysunek 5.3. Zapiszmy go w kanonicznej formie (5.4):
, patrz rysunek 5.3. Zapiszmy go w kanonicznej formie (5.4):
Zbadajmy trzy punktu tego zbioru ![]() ,
, ![]() i
i ![]() .
.
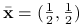 :
: 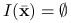 i
i 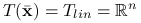 .
.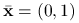 :
: 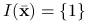 ,
, 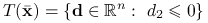 ,
,![T_{{lin}}({\bar{\mathbf{x}}})=\{\mathbf{d}\in\mathbb{R}^{2}:\ Dg_{1}(0,1)\mathbf{d}\le 0\}=\{\mathbf{d}\in\mathbb{R}^{2}:\ [0,2]\mathbf{d}\le 0\}=T({\bar{\mathbf{x}}}).](wyklady/op2/mi/mi920.png)
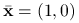 :
: 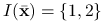 ,
, 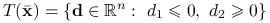 ,
,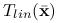
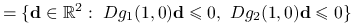
![\displaystyle=\{\mathbf{d}\in\mathbb{R}^{2}:\ [2,0]\mathbf{d}\le 0,\ [0,-1]\mathbf{d}\le 0\}=T({\bar{\mathbf{x}}}).](wyklady/op2/mi/mi989.png)
Przykład 5.4
Rozważmy ten sam zbiór ![]() co w powyższym przykładzie, lecz zapiszmy go nieco inaczej:
co w powyższym przykładzie, lecz zapiszmy go nieco inaczej:
Zmianie uległo drugie ograniczenie: z ![]() na
na ![]() . Nowy opis zbioru
. Nowy opis zbioru ![]() odpowiada ograniczeniom
odpowiada ograniczeniom ![]() ,
, ![]() . Rozważmy zbiory
. Rozważmy zbiory ![]() i
i ![]() w punkcie
w punkcie ![]() . Stożek kierunków stycznych jest identyczny, gdyż zbiór się nie zmienił:
. Stożek kierunków stycznych jest identyczny, gdyż zbiór się nie zmienił:
Natomiast stożek kierunków stycznych dla ograniczeń zlinearyzowanych jest następujący:
Widzimy zatem, że nie zawsze zachodzi równość pomiędzy ![]() i
i ![]() .
.
5.3. Warunki konieczne Kuhna-Tuckera
W lemacie 5.2 wykazaliśmy, że ![]() . Pokazaliśmy w przykładach, że dość często mamy równość tych dwóch zbiorów. Okazuje się, że to bardzo ważna własność, która będzie punktem wyjścia dla całej teorii optymalizacji nieliniowej Kuhna-Tucker'a. Zanim jednak przejdziemy do głównego twierdzenia dowiedziemy pomocniczy, lecz bardzo ważny lemat.
. Pokazaliśmy w przykładach, że dość często mamy równość tych dwóch zbiorów. Okazuje się, że to bardzo ważna własność, która będzie punktem wyjścia dla całej teorii optymalizacji nieliniowej Kuhna-Tucker'a. Zanim jednak przejdziemy do głównego twierdzenia dowiedziemy pomocniczy, lecz bardzo ważny lemat.
Lemat 5.3 (Farkas (1901))
Niech ![]() będzie macierzą
będzie macierzą ![]() i
i ![]() . Wówczas dokładnie jeden z układów ma rozwiązanie:
. Wówczas dokładnie jeden z układów ma rozwiązanie:
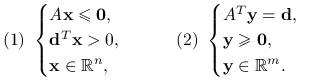 |
Dowód
Pokażemy najpierw, że jeśli układ (2) ma rozwiązanie, to układ (1) go nie ma. Weźmy zatem ![]() spełniające (2). Zatem
spełniające (2). Zatem ![]() . Wstawiamy to do układu (1) i otrzymujemy
. Wstawiamy to do układu (1) i otrzymujemy
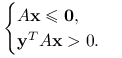 |
Pierwsza nierówność oznacza, że każda współrzędna wektora ![]() jest niedodatnia. Ponieważ współrzędne
jest niedodatnia. Ponieważ współrzędne ![]() są nieujemne, to iloczyn skalarny
są nieujemne, to iloczyn skalarny ![]() jest niedodatni. Przeczy to drugiej nierówności, a zatem dowodzi, że (1) nie ma rozwiązania.
jest niedodatni. Przeczy to drugiej nierówności, a zatem dowodzi, że (1) nie ma rozwiązania.
Załóżmy teraz, że układ (2) nie ma rozwiązania. Zdefiniujmy zbiór
Łatwo sprawdzić, że jest to zbiór wypukły i domknięty. Z faktu, że układ (2) nie ma rozwiązania wynika, że ![]() . Zastosujmy więc mocne twierdzenia o oddzielaniu, tw. 3.2 do zbiorów
. Zastosujmy więc mocne twierdzenia o oddzielaniu, tw. 3.2 do zbiorów ![]() i
i ![]() . Istnieje więc wektor
. Istnieje więc wektor ![]() taki że
taki że
Pokażemy, że ![]() jest rozwiązaniem układu (1). Oznaczmy
jest rozwiązaniem układu (1). Oznaczmy ![]() . Ponieważ
. Ponieważ ![]() , to
, to ![]() , co pociąga
, co pociąga ![]() . Pozostaje tylko udowodnić, że
. Pozostaje tylko udowodnić, że ![]() . Przypuśćmy, że
. Przypuśćmy, że ![]() -ta współrzędna
-ta współrzędna ![]() jest dodatnia. Z definicji zbioru
jest dodatnia. Z definicji zbioru ![]() wynika, że dla dowolnego
wynika, że dla dowolnego ![]() zachodzi
zachodzi ![]() . Zdefiniujmy ciąg
. Zdefiniujmy ciąg ![]() , gdzie
, gdzie ![]() jest na
jest na ![]() -tej współrzędnej. Na mocy założenia o dodatniości
-tej współrzędnej. Na mocy założenia o dodatniości ![]() dostajemy
dostajemy
co przeczy temu, że ![]() . Sprzeczność ta dowodzi, że
. Sprzeczność ta dowodzi, że ![]() .
.
Twierdzenie 5.2 (Twierdzenie Kuhna-Tuckera)
Niech ![]() będzie rozwiązaniem lokalnym (5.3). Jeśli funkcje
będzie rozwiązaniem lokalnym (5.3). Jeśli funkcje ![]() oraz
oraz ![]() ,
, ![]() , są różniczkowalne w
, są różniczkowalne w ![]() oraz
oraz ![]() , to istnieje
, to istnieje ![]() , takie że
, takie że
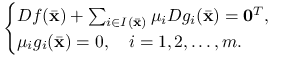 |
(5.5) |
Często tezę powyższego twierdzenia zapisuje się biorąc sumę po wszystkich ![]() :
:
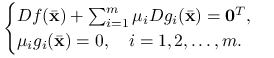 |
Jest to naginanie notacji, gdyż funkcje opisujące ograniczenia nieaktywne nie muszą być różniczkowalne w punkcie ![]() . Z drugiej strony są one mnożone przez zerowe współczynniki
. Z drugiej strony są one mnożone przez zerowe współczynniki ![]() . Jest to pewne usprawiedliwienie powyższej notacji, którą należy rozumieć tak, jak zapisane zostało w twierdzeniu 5.2.
. Jest to pewne usprawiedliwienie powyższej notacji, którą należy rozumieć tak, jak zapisane zostało w twierdzeniu 5.2.
Dowód twierdzenia 5.2
Na mocy twierdzenia 5.1 mamy ![]() . Dalej, korzystając z założenia, dostajemy
. Dalej, korzystając z założenia, dostajemy ![]() , co innymi słowy oznacza, że nie istnieje rozwiązanie
, co innymi słowy oznacza, że nie istnieje rozwiązanie ![]() układu
układu
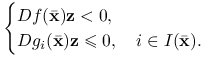 |
Stosujemy lemat Farkasa z ![]() i macierzą
i macierzą ![]() złożoną wierszowo z gradientów ograniczeń aktywnych
złożoną wierszowo z gradientów ograniczeń aktywnych ![]() ,
, ![]() . Istnieje zatem
. Istnieje zatem ![]() takie że
takie że ![]() lub inaczej
lub inaczej
Zdefiniujmy ![]() następująco:
następująco: ![]() i
i ![]() . Wówczas powyższa równość jest równoważna następującej
. Wówczas powyższa równość jest równoważna następującej
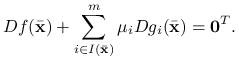 |
Z definicji ![]() oczywiste jest, że
oczywiste jest, że ![]() .
.
Uwaga 5.1
Założenia twierdzenia Kuhna-Tuckera są trywialnie spełnione, gdy ![]() , tzn. gdy
, tzn. gdy ![]() . Wówczas warunki (5.5) sprowadzają się do
. Wówczas warunki (5.5) sprowadzają się do
Na zakończenie zwróćmy jeszcze raz uwagę na tezę twierdzenia Kuhna-Tuckera. Warunki (5.5) nazywane są warunkami koniecznymi pierwszego rzędu. Wektor ![]() będzie pojawiał się jeszcze wiele razy na tym wykładzie. Nadajmy mu zatem nazwę:
będzie pojawiał się jeszcze wiele razy na tym wykładzie. Nadajmy mu zatem nazwę:
Definicja 5.5
Wektor ![]() spełniający (5.5) nazywa się wektorem mnożników Lagrange'a w punkcie
spełniający (5.5) nazywa się wektorem mnożników Lagrange'a w punkcie ![]() .
.
5.4. Zadania
Ćwiczenie 5.1
Wykaż, że zbiór ![]() dla
dla ![]() jest stożkiem.
jest stożkiem.
Ćwiczenie 5.2
Udowodnij, że stożek kierunków stycznych ![]() jest zbiorem domkniętym.
jest zbiorem domkniętym.
Ćwiczenie 5.3
Udowodnij tożsamość (5.2).
Ćwiczenie 5.4
Znajdź stożek kierunków stycznych do zbioru ![]() w punkcie
w punkcie ![]() , gdy
, gdy
Ćwiczenie 5.5
Udowodnić, że dla zadania
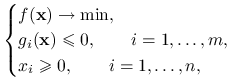 |
warunek konieczny pierwszego rzędu przyjmuje postać:
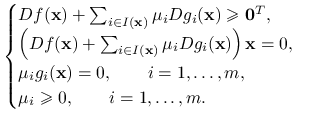 |
Nierówność dla wektorów oznacza nierówność po współrzędnych.