Zagadnienia

9.1 Warunki drugiego rzędu
9.2 Podsumowanie
9.3 Przykład
9.4 Zadania

9. Warunki drugiego rzędu

W tym rozdziale przedstawimy warunki konieczne i dostateczne drugiego rzędu, tzn. warunki sformułowane w języku drugich pochodnych oraz podsumujemy dotychczasową wiedzę dotyczącą rozwiązywania problemów optymalizacyjnych z ograniczeniami mieszanymi.

9.1. Warunki drugiego rzędu

Rozważmy problem optymalizacyjny z ograniczeniami mieszanymi (8.1). Załóżmy, że pewnym punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest warunek pierwszego rzędu, tzn. istnieją wektory $\mu\in[0,\infty)^{m}$ i $\lambda\in\mathbb{R}^{l}$ , takie że

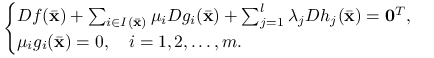$\begin{cases}Df({\bar{\mathbf{x}}})+\sum _{{i\in I({\bar{\mathbf{x}}})}}\mu _{i}Dg_{i}({\bar{\mathbf{x}}})+\sum _{{j=1}}^{l}\lambda _{j}Dh_{j}({\bar{\mathbf{x}}})=\mathbf{0}^{T},&\\ \mu _{i}g_{i}({\bar{\mathbf{x}}})=0,\quad i=1,2,\ldots,m.&\end{cases}$

Definicja 9.1

Funkcją Lagrange'a nazywamy funkcję

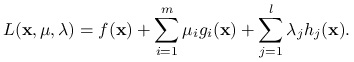$L(\mathbf{x},\mu,\lambda)=f(\mathbf{x})+\sum _{{i=1}}^{m}\mu _{i}g_{i}(\mathbf{x})+\sum _{{j=1}}^{l}\lambda _{j}h_{j}(\mathbf{x}).$

Możemy teraz zapisać warunek pierwszego rzędu w skróconej formie:

$D_{x}L({\bar{\mathbf{x}}},\mu,\lambda)=\mathbf{0}^{T},\qquad\text{oraz}\qquad\mu _{i}g_{i}({\bar{\mathbf{x}}})=0,\quad i=1,2,\ldots,m,$

gdzie $D_{x}$ oznacza różniczkowanie względem zmiennej $\mathbf{x}\in\mathbb{R}^{n}$ .

Definicja 9.2

Zbiór

$I^{*}({\bar{\mathbf{x}}})=\big\{ i\in I({\bar{\mathbf{x}}}):\ \mu _{i}>0\big\}$

nazywamy zbiorem ograniczeń nierównościowych mocno aktywnych.

Zbiór

$I^{0}({\bar{\mathbf{x}}})=I({\bar{\mathbf{x}}})\setminus I^{*}({\bar{\mathbf{x}}})$

nazywamy zbiorem ograniczeń nierównościowych słabo aktywnych.

Twierdzenie 9.1 (Warunek konieczny drugiego rzędu)

Załóżmy, że punkt ${\bar{\mathbf{x}}}$ jest lokalnym rozwiązaniem problemu z ograniczeniami mieszanymi i spełniony jest w nim warunek liniowej niezależności. Niech $\mu$ , $\lambda$ będą mnożnikami Lagrange'a z warunku pierwszego rzędu. Jeśli $f$ , $g_{i}$ , $i\in I({\bar{\mathbf{x}}})$ oraz $h_{j}$ , $j=1,\ldots,l$ , są klasy $C^{2}$ w otoczeniu ${\bar{\mathbf{x}}}$ , to

$\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}\ge 0$

dla każdego $\mathbf{d}\in\mathbb{R}^{n}$ spełniającego

		$\displaystyle Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad i\in I({\bar{\mathbf{x}}}),$
		$\displaystyle Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad j=1,\ldots,l.$

Dowód

Ustalmy $\mathbf{d}\in\mathbb{R}^{n}$ jak w warunkach twierdzenia. Na mocy twierdzenia 8.5 istnieje $\varepsilon>0$ i krzywa $\mathbf{y}:(-\varepsilon,\varepsilon)\to\mathbb{R}^{n}$ klasy $C^{2}$ o następujących własnościach: $\mathbf{y}(0)={\bar{\mathbf{x}}}$ , $y^{{\prime}}(0)=\mathbf{d}$ , oraz dla $t\in(-\varepsilon,\varepsilon)$ mamy $h_{j}(y(t))=0$ , $j=1,\ldots,l$ , i $g_{i}(y(t))=0$ , $i\in I({\bar{\mathbf{x}}}).$ Wynika stąd, że funkcja $F(t):=L(y(t),\mu,\lambda)$ równa jest $f(y(t))$ dla $t$ w otoczeniu $0$ . Z ciągłości ograniczeń nieaktywnych wnioskujemy, że $y(t)\in W$ dla $t$ w otoczeniu $0$ . Zatem $F$ ma minimum lokalne w $0$ , gdyż $y(0)$ jest minimum lokalnym $f$ na $W.$ Na mocy założeń, $F$ jest klasy $C^{2}$ . Istnienie minimum w zerze implikuje, że $F^{{\prime\prime}}(0)\ge 0$ , a więc

$0\le\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}+D_{x}L({\bar{\mathbf{x}}},\mu,\lambda)y^{{\prime\prime}}(0).$

To kończy dowód, gdyż w punkcie ${\bar{\mathbf{x}}}$ spełnione są warunki pierwszego rzędu: $D_{x}L({\bar{\mathbf{x}}},\mu,\lambda)=\mathbf{0}^{T}$ .

∎

Bez dowodu pozostawiamy następujące uogólnienie powyższego twierdzenia:

Twierdzenie 9.2

Przy założeniach tw. 9.1 następująca nierówność

$\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}\ge 0$

zachodzi dla każdego $\mathbf{d}\in\mathbb{R}^{n}$ spełniającego

		$\displaystyle Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad i\in I^{*}({\bar{\mathbf{x}}}),$
		$\displaystyle Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}\le 0,\quad i\in I^{0}({\bar{\mathbf{x}}}),$
		$\displaystyle Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad j=1,\ldots,l.$

Podamy teraz warunek dostateczny istnienia rozwiązania lokalnego. Zwróćmy uwagę na to, że warunek ten implikuje, iż rozwiązanie jest ścisłe. Pozostaje więc szara strefa, gdzie jest spełniony warunek konieczny drugiego rzędu, lecz nie zachodzi warunek dostateczny drugiego rzędu. Podobnie jak w przypadku optymalizacji bez ograniczeń, na to nie ma niestety rady.

Twierdzenie 9.3 (Warunek dostateczny drugiego rzędu)

Załóżmy, że w punkcie ${\bar{\mathbf{x}}}\in W$ spełniony jest warunek pierwszego rzędu, tzn. istnieją wektory $\mu\in[0,\infty)^{m}$ i $\lambda\in\mathbb{R}^{l}$ , takie że

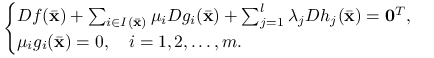(9.1)

Załóżmy ponadto, że funkcje $g_{i}$ , $i\in I^{*}({\bar{\mathbf{x}}})$ , oraz $h_{j}$ , $j=1,\ldots,l,$ są dwukrotnie różniczkowalne w ${\bar{\mathbf{x}}}$ . Jeśli

$\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}>0$

dla każdego $\mathbf{d}\in\mathbb{R}^{n}\setminus\mathbf{0}$ spełniającego

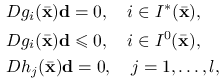$\begin{aligned}\displaystyle&\displaystyle Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad i\in I^{*}({\bar{\mathbf{x}}}),\\ \displaystyle&\displaystyle Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}\le 0,\quad i\in I^{0}({\bar{\mathbf{x}}}),\\ \displaystyle&\displaystyle Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad j=1,\ldots,l,\end{aligned}$

(9.2)

to ${\bar{\mathbf{x}}}$ jest ścisłym rozwiązaniem lokalnym.

Zanim przejdziemy do dowodu podkreślmy, iż w powyższym twierdzeniu nie zakłada się regularności punktu ograniczeń.

Dowód twierdzenia 9.3

Przeprowadzimy dowód przez zaprzeczenie. Załóżmy mianowicie, że ${\bar{\mathbf{x}}}$ nie jest ścisłym rozwiązaniem lokalnym. Istnieje zatem ciąg punktów dopuszczalnych $\mathbf{x}_{k}\in W$ , takich że $\mathbf{x}_{k}\ne{\bar{\mathbf{x}}}$ oraz $f(\mathbf{x}_{k})\le f({\bar{\mathbf{x}}})$ . Zdefiniujmy

$\mathbf{d}_{k}=\frac{\mathbf{x}_{k}-{\bar{\mathbf{x}}}}{\|\mathbf{x}_{k}-{\bar{\mathbf{x}}}\|},\qquad\text{oraz}\qquad\lambda _{k}=\|\mathbf{x}_{k}-{\bar{\mathbf{x}}}\|.$

Wówczas $\mathbf{x}_{k}={\bar{\mathbf{x}}}+\lambda _{k}\mathbf{d}_{k}$ . Zauważmy, że $\lim _{{k\to\infty}}\lambda _{k}=0$ . Z faktu $\|\mathbf{d}_{k}\|=1$ wynika, że istnieje podciąg $\mathbf{d}_{{k_{n}}}$ zbieżny do pewnego $\mathbf{d}$ o normie jednostkowej. Aby uprościć notację zakładamy, że od początku $\mathbf{d}_{k}$ był zbieżny do $\mathbf{d}$ . Oczywiście z definicji $\lambda _{k}$ wynika, że $\lim _{{k\to\infty}}\lambda _{k}=0.$

W dalszej części dowodu wykażemy dwie własności $\mathbf{d}$ : (a) $\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}\le 0$ oraz (b) $\mathbf{d}$ spełnia warunki (9.2). A to przeczy założeniom twierdzenia.

Rozpocznijmy od dowodu własności (a). Z definicji drugiej pochodnej:

$L(\mathbf{x},\mu,\lambda)=L({\bar{\mathbf{x}}},\mu,\lambda)+D_{x}L({\bar{\mathbf{x}}},\mu,\lambda)(\mathbf{x}-{\bar{\mathbf{x}}})+\frac{1}{2}(\mathbf{x}-{\bar{\mathbf{x}}})^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)(\mathbf{x}-{\bar{\mathbf{x}}})+o(\|\mathbf{x}-{\bar{\mathbf{x}}}\|^{2}).$

Przypomnijmy, że $L(\mathbf{x}_{k},\mu,\lambda)\le L({\bar{\mathbf{x}}},\mu,\lambda)$ , bo $f(\mathbf{x}_{k})\le f({\bar{\mathbf{x}}})$ oraz $g_{i}(\mathbf{x}_{k})\le g_{i}({\bar{\mathbf{x}}})$ dla $i\in I({\bar{\mathbf{x}}})$ . Z warunku pierwszego rzędu (9.1) wynika również, że $D_{x}L({\bar{\mathbf{x}}},\mu,\lambda)=\mathbf{0}^{T}$ . Zatem

$(\mathbf{x}_{k}-{\bar{\mathbf{x}}})^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)(\mathbf{x}_{k}-{\bar{\mathbf{x}}})+o(\|\mathbf{x}_{k}-{\bar{\mathbf{x}}}\|^{2})\le 0.$

Przypomnijmy, że $\mathbf{x}_{k}={\bar{\mathbf{x}}}+\lambda _{k}\mathbf{d}_{k}$ . Wstawiając tą reprezentację do powyższego wzoru dostajemy:

$\lambda _{k}^{2}\mathbf{d}_{k}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}_{k}+o(\lambda _{k}^{2}\|\mathbf{d}_{k}\|^{2})\le 0.$

Dzielimy obie strony przez $\lambda _{k}^{2}$ :

$\mathbf{d}_{k}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}_{k}+\frac{o(\lambda _{k}^{2}\|\mathbf{d}_{k}\|^{2})}{\lambda _{k}^{2}}\le 0.$

Przypomnijmy, że $\|\mathbf{d}_{k}\|=1$ . A zatem w granicy, gdy $k\to\infty$ , drugi składnik powyższej sumy dąży do $0$ . Korzystając z faktu, że $\lim _{{k\to\infty}}\mathbf{d}_{k}=\mathbf{d}$ dostajemy

$\mathbf{d}^{T}D^{2}_{x}L({\bar{\mathbf{x}}},\mu,\lambda)\mathbf{d}\le 0,$

co kończy dowód faktu (a).

W dowodzie własności (b) zastosujemy podobne podejście jak powyżej. Z różniczkowalności funkcji $f$ w punkcie ${\bar{\mathbf{x}}}$ mamy

$f(\mathbf{x}_{k})=f({\bar{\mathbf{x}}})+Df({\bar{\mathbf{x}}})(\mathbf{x}_{k}-{\bar{\mathbf{x}}})+o(\|\mathbf{x}_{k}-{\bar{\mathbf{x}}}\|).$

Przypomnijmy, że $f(\mathbf{x}_{k})\le f({\bar{\mathbf{x}}})$ , co implikuje

$Df({\bar{\mathbf{x}}})(\mathbf{x}_{k}-{\bar{\mathbf{x}}})+o(\|\mathbf{x}_{k}-{\bar{\mathbf{x}}}\|)\le 0.$

Korzystając znów z reprezentacji $\mathbf{x}_{k}={\bar{\mathbf{x}}}+\lambda _{k}\mathbf{d}_{k}$ dostajemy

$Df({\bar{\mathbf{x}}})\mathbf{d}_{k}+\frac{o(\lambda _{k}\|\mathbf{d}_{k}\|)}{\lambda _{k}}\le 0.$

Zatem w granicy, przy $k\to\infty$ , otrzymujemy $Df({\bar{\mathbf{x}}})\mathbf{d}\le 0$ . Zauważając, że $g_{i}(\mathbf{x}_{k})\le g_{i}({\bar{\mathbf{x}}})=0$ dla $i\in I({\bar{\mathbf{x}}})$ i postępując podobnie jak powyżej dostajemy $Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}\le 0$ , $i\in I({\bar{\mathbf{x}}})$ . Analogicznie również dowodzimy, że $Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0$ dla $j=1,\ldots,l.$

Pomnóżmy obie strony pierwszej równości w (9.1) przez $\mathbf{d}$ :

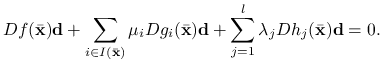$Df({\bar{\mathbf{x}}})\mathbf{d}+\sum _{{i\in I({\bar{\mathbf{x}}})}}\mu _{i}Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}+\sum _{{j=1}}^{l}\lambda _{j}Dh_{j}({\bar{\mathbf{x}}})\mathbf{d}=0.$

Suma ta składa się z wyrazów nieujemnych. Ponieważ sumują się one do zera, to wszystkie muszą być zerowe. W szczególności

$Df({\bar{\mathbf{x}}})\mathbf{d}=0,\qquad\text{oraz}\qquad Dg_{i}({\bar{\mathbf{x}}})\mathbf{d}=0,\quad i\in I^{*}({\bar{\mathbf{x}}}).$

Dowiedliśmy zatem, że $\mathbf{d}$ spełnia warunki (9.2).

∎

9.2. Podsumowanie

Opiszemy teraz ogólny algorytm postępowania w przypadku rozwiązywania problemów optymalizacyjnych z ograniczeniami mieszanymi.

Krok 1. Szukamy punktów podejrzanych:

	$\displaystyle A_{1}=\{\mathbf{x}\in X:$	$\displaystyle\text{w punkcie $\mathbf{x}$ \textbf{nie} zachodzi warunek regularności}\},$
	$\displaystyle A_{2}=\{\mathbf{x}\in X:$	w punkcie $\mathbf{x}$ zachodzi warunek regularności
		$\displaystyle\text{i spełnione są warunki pierwszego rzędu}\}.$

Krok 2. Sprawdzamy, czy w punktach ze zbiorów $A_{1},A_{2}$ spełnione są założenia tw. 7.6, tzw. warunki dostateczne pierwszego rzędu. Jeśli tak, to w punktach tych są rozwiązania globalne. Pozostałe kroki podejmujemy, jeśli

nie znaleźliśmy żadnego rozwiązania globalnego, lub
chcemy znaleźć wszystkie rozwiązania globalne, lub
chcemy znaleźć wszystkie rozwiązania lokalne.

Usuwamy ze zbiorów $A_{1},A_{2}$ punkty, które są rozwiązaniami globalnymi. Oznaczmy nowe zbiory $A^{{\prime}}_{1},A^{{\prime}}_{2}$ .

Krok 3. Eliminujemy ze zbioru $A^{{\prime}}_{2}$ te punkty, gdzie nie zachodzi warunek konieczny drugiego rzędu. Pozostałe punkty oznaczamy $A^{{\prime\prime}}_{2}.$

Krok 4. W każdym punkcie ze zbioru $A^{{\prime}}_{1}\cap A^{{\prime\prime}}_{2}$ sprawdzamy warunek dostateczny drugiego rzędu. Punkty, w których jest spełniony, są rozwiązaniami lokalnymi.

Krok 5. Optymalność punktów ze zbioru $A^{{\prime}}_{1}\cap A^{{\prime\prime}}_{2}$ , w których nie jest spełniony warunek dostateczny drugiego rzędu sprawdzamy innymi metodami.

9.3. Przykład

W tym podrozdziale opiszemy bardzo dokładnie rozwiązanie następującego problemu optymalizacyjnego:

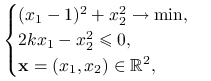$\begin{cases}(x_{1}-1)^{2}+x_{2}^{2}\to\min,&\\ 2kx_{1}-x_{2}^{2}\le 0,&\\ \mathbf{x}=(x_{1},x_{2})\in\mathbb{R}^{2},&\end{cases}$

gdzie $k>0$ jest parametrem.

Zauważmy, że w każdym punkcie, gdzie aktywne jest ograniczenie, spełniony jest warunek liniowej niezależności ograniczeń: pierwsza pochodna ograniczenia wynosi $[2k,-2x_{2}]\ne\mathbf{0}^{T}$ . Wynika stąd, że $A_{1}=\emptyset.$

Funkcja Lagrange'a dla powyższego problemu ma postać:

$L(x_{1},x_{2};\mu)=(x_{1}-1)^{2}+x_{2}^{2}+\mu(2kx_{1}-x_{2}^{2}).$

Zapiszmy warunek pierwszego rzędu:

		$\displaystyle[2(x_{1}-1),2x_{2}]+\mu[2k,-2x_{2}]=\mathbf{0}^{T},$		(9.3)
		$\displaystyle\mu(2kx_{1}-x_{2}^{2})=0,$		(9.4)
		$\displaystyle\mu\ge 0.$

Sprawdźmy, czy możliwe jest $\mu=0$ . Wówczas z równania (9.3) dostajemy

$2(x_{1}-1)=0,\qquad 2x_{2}=0,$

co pociąga $x_{1}=1,$ $x_{2}=0.$ Punkt ten nie jest dopuszczalny: nie spełnia warunku nierównościowego dla żadnego $k>0$ . Wnioskujemy zatem, że $\mu>0$ i warunek konieczny pierwszego rzędu może być spełniony tylko w punktach, w których ograniczenie nierównościowe jest aktywne:

$2kx_{1}-x_{2}^{2}=0.$

(9.5)

Rozpiszmy równanie (9.3):

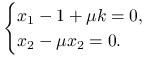$\begin{cases}x_{1}-1+\mu k=0,&\\ x_{2}-\mu x_{2}=0.&\end{cases}$

Z drugiego równania wynika, że albo $\mu=1$ albo $x_{2}=0.$ Jeśli $x_{2}=0,$ to z (9.5) dostajemy $x_{1}=0.$ Punkt $(0,0)$ wraz z mnożnikiem Lagrange'a $\mu=1/k$ spełnia warunek pierwszego rzędu.

Rozważmy teraz przypadek $\mu=1$ . Wówczas z równania $x_{1}-1+\mu k=0$ dostajemy $x_{1}=1-k.$ Jeśli $k>1$ , to $x_{1}<0$ i równanie (9.5) nie ma rozwiązania. Dla $k=1$ dostajemy punkt $(0,0)$ , zaś dla $k\in(0,1)$ dwa punkty

$x_{1}=1-k,\qquad x_{2}=\pm\sqrt{2k(1-k)}.$

Podsumowując: $A_{1}=\emptyset$ oraz

		$\displaystyle A_{2}=\{(0,0)\}\qquad\text{dla}\quad k\ge 1,$
		$\displaystyle A_{2}=\big\{(0,0),\big(1-k,\sqrt{2k(1-k)}\big),\big(1-k,-\sqrt{2k(1-k)}\big)\big\}\qquad\text{dla}\quad 0<k<1.$

Funkcja $g_{1}(x_{1},x_{2})=2kx_{1}-x_{2}^{2}$ nie jest quasi-wypukła, wiec nie możemy skorzystać z twierdzenia 7.6 stwierdzającego dostateczność warunku pierwszego rzędu. Zatem $A^{{\prime}}_{2}=A_{2}$ .

Przechodzimy do kroku 3 i sprawdzamy warunek konieczny drugiego rzędu dla punktów z $A^{{\prime}}_{2}$ . Rozważmy najpierw punkt $(0,0).$ Odpowiada mu mnożnik Lagrange'a $\mu=1/k.$ Pierwsza pochodna funkcji Lagrange'a ma postać:

$D_{x}L(x_{1},x_{2},1/k)=[(2(x_{1}-1)+2,2x_{2}(1-\frac{1}{k})].$

Macierz drugich pochodnych to;

$D^{2}_{x}L(x_{1},x_{2},1/k)=\begin{bmatrix}2,&0\\ 0,&2(1-\frac{1}{k})\end{bmatrix}.$

Na mocy twierdzenia wystarczy sprawdzić, że

$\mathbf{d}^{T}\begin{bmatrix}2,&0\\ 0,&2(1-\frac{1}{k})\end{bmatrix}\mathbf{d}\ge 0$

dla wektorów $\mathbf{d}\in\mathbb{R}^{2}\setminus\mathbf{0}$ spełniających $Dg_{1}(0,0)\mathbf{d}=[2k,0]\mathbf{d}=0$ , czyli takich że $d_{1}=0.$ Wstawiając do powyższej nierówności dostajemy $(1-\frac{1}{k})d_{2}^{2}\ge 0.$ Nierówność ta zachodzi dla $k\ge 1$ : w punkcie $(0,0)$ może być rozwiązanie lokalne. Dla $k<1$ nierówność nie zachodzi, więc w $(0,0)$ nie ma rozwiązania lokalnego.

Załóżmy teraz $0<k<1$ i rozważmy dwa pozostałe punkty. W obu przypadkach mnożnik Lagrange'a $\mu=1$ . Mamy zatem

		$\displaystyle D_{x}L(x_{1},x_{2},1)=[(2(x_{1}-1)+2k,0],$
		$\displaystyle D^{2}_{x}L(x_{1},x_{2},1)=\begin{bmatrix}2,&0\\ 0,&0\end{bmatrix}.$

Macierz drugich pochodnych jest nieujemnie określona, więc warunek konieczny drugiego rzędu jest spełniony w obu punktach. Podsumowując:

		$\displaystyle A^{{\prime\prime}}_{2}=\{(0,0)\}\qquad\text{dla}\quad k\ge 1,$
		$\displaystyle A^{{\prime\prime}}_{2}=\big\{\big(1-k,\sqrt{2k(1-k)}\big),\big(1-k,-\sqrt{2k(1-k)}\big)\big\}\qquad\text{dla}\quad 0<k<1.$

Przechodzimy do sprawdzenia warunku dostatecznego drugiego rzędu. W przypadku $k>1$ macierz drugich pochodnych funkcji Lagrange'a jest dodatnio określona, więc na mocy tw. 9.3 w punkcie $(0,0)$ jest ścisłe rozwiązanie lokalne. Niestety nie możemy nic powiedzieć o punkcie $(0,0)$ , gdy $k=1.$

Rozważmy przypadek $0<k<1.$ Zajmijmy się punktem ${\bar{\mathbf{x}}}=\big(1-k,\sqrt{2k(1-k)}\big).$ Musimy sprawdzić warunki tw. 9.3:

$\mathbf{d}^{T}\begin{bmatrix}2,&0\\ 0,&0\end{bmatrix}\mathbf{d}=2d_{1}^{2}>0$

dla $\mathbf{d}\in\mathbb{R}^{2}\setminus\mathbf{0}$ spełniającego $[2k,-2\sqrt{2k(1-k)}]\mathbf{d}=0,$ czyli $d_{1}=\frac{1}{k}\sqrt{2k(1-k)}d_{2}.$ A zatem jeśli $\mathbf{d}\ne\mathbf{0}$ , to $d_{1}\ne 0$ i w punkcie ${\bar{\mathbf{x}}}$ spełniony jest warunek dostateczny drugiego rzędu: ${\bar{\mathbf{x}}}$ jest ścisłym rozwiązaniem lokalnym. Analogicznie dowodzimy, że punkt $\big(1-k,-\sqrt{2k(1-k)}\big)$ jest również ścisłym rozwiązaniem lokalnym.

Pozostaje jeszcze przypadek $k=1.$ Choć $(0,0)$ jest rozwiązaniem globalnym, to nie udało nam się tego pokazać korzystając z teorii Kuhna-Tuckera. Łatwo można to jednak udowodnić bezpośrednio.

9.4. Zadania

Ćwiczenie 9.1

Rozwiąż geometrycznie i analitycznie zadanie minimalizacji $x_{2}$ na zbiorze $W=\{(x_{1},x_{2}):\ x_{1}+x_{2}\ge 2,\ x_{1}^{2}+x_{2}^{2}\le 2\}.$

Ćwiczenie 9.2

Niech $A$ będzie macierzą $m\times n$ o pełnym rzędzie (tzn. o rzędzie równym $\min(m,n)$ ). Udowodnij, że rzut na jądro $\ker A$ jest przekształceniem liniowym zadanym wzorem

$I-A^{T}(AA^{T})^{{-1}}A.$

W dowodzie wykorzystaj fakt, że rzeczony rzut, to taki punkt zbioru $\ker A$ , który jest najmniej oddalony od rzutowanego punktu.

Ćwiczenie 9.3

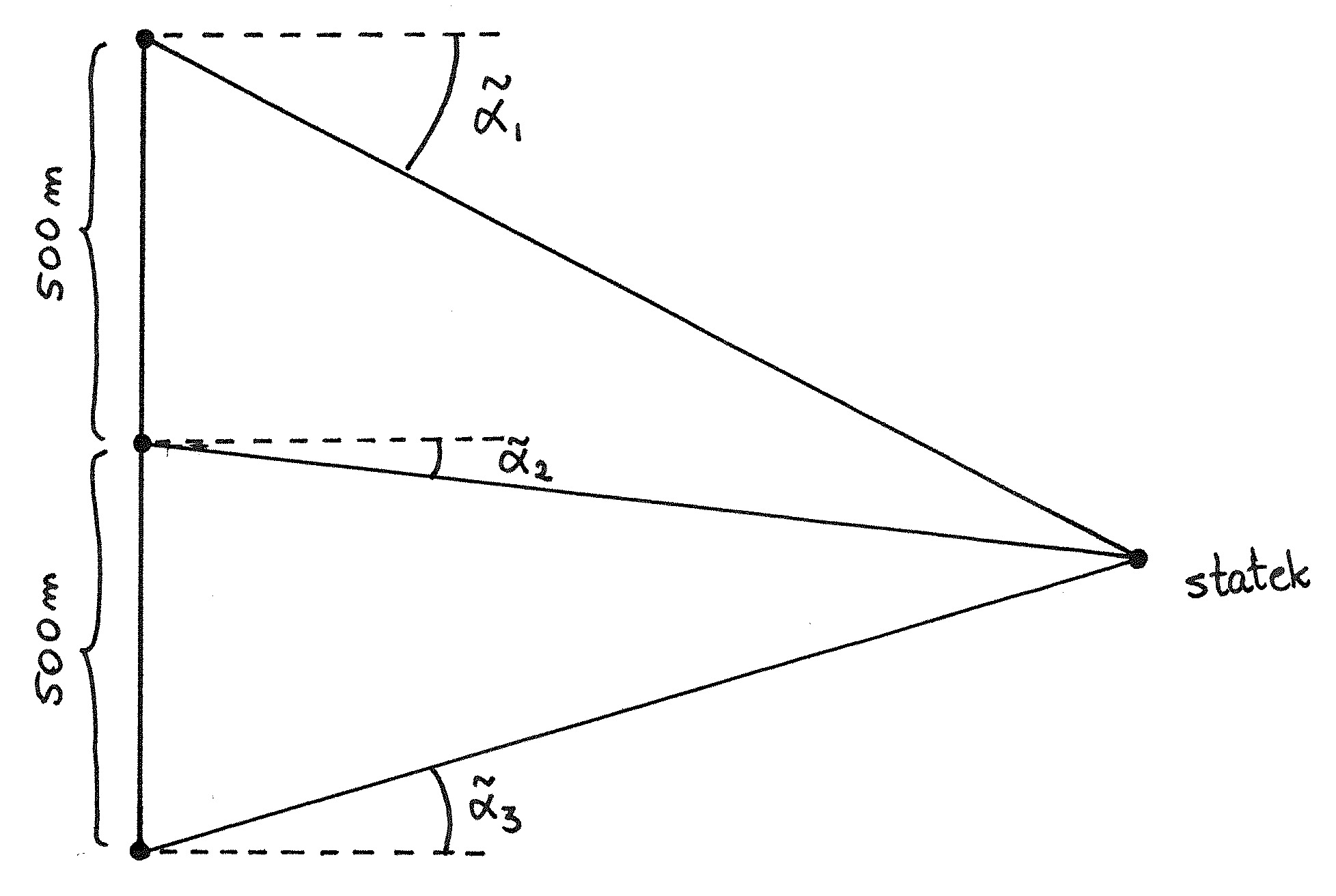
$Rysunek pomocniczy do zadania \ref{exe:ch9:statek}$

Rys. 9.1. Położenie punktów pomiarowych.

Na brzegu będącym prostym odcinkiem co $500$ metrów stoją trzy stacje pomiarowe, patrz rys. 9.1. Każda z nich mierzy kąt między prostą prostopadłą do brzegu a prostą przechodzącą przez punkt pomiarowy i statek. Wyniki obserwacji są następujące:

$\tilde{\alpha}_{1}=0.083,\qquad\tilde{\alpha}_{2}=0.024,\qquad\tilde{\alpha}_{3}=-0.017.$

Pomiary te są obarczone małymi błędami. Skoryguj je tak, aby były zgodne tzn. wskazywały na ten sam punkt na płaszczyźnie i korekta była jak najmniejsza w sensie średniokwadratowym (suma kwadratów różnic pomiędzy zmierzonymi kątami i skorygowanymi kątami). Znajdź położenie statku względem punktów pomiarowych. W obliczeniach przyjmij, że $tg(\alpha)\approx\alpha$ dla małych kątów $\alpha$ .

Ćwiczenie 9.4

Metalowa belka ma przekrój trapezoidalny. Pole tego przekroju ze względów wytrzymałościowych musi wynosić $S$ . Górna i boczna powierzchnia musi zostać zabezpieczona antykorozyjnie. Ustal tak kształt przekroju, aby powierzchnia do zabezpieczenia antykorozyjnego była jak najmniejsza.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Optymalizacja II