10. Wykład X, 4.XII.2009

Pod koniec Wykładu IX poznaliśmy już pewne zastosowanie fundamentalnego Twierdzenia 9.2 (pochodzącego od Karusha i Kuhna-Tuckera, podanego w Wykładzie IX w w formacie `wteddy' w wersji z obiektami wklęsłymi/wypukłymi), co prawda zastosowanie dość odległe od analizy portfelowej.
Nasuwa się przy tej okazji pytanie, czy może czytelnik umie rozwiązać Ćwiczenie 9.5 (Wykład IX) bez Twierdzenia 9.2? Jeśli nie, to skromniejsze pytanie mogłoby brzmieć tak: czy w rozwiązaniu Ćwiczenia 9.5 podanym w Wykładzie IX koniecznych jest dziesięć warunków nierównościowych? Np zmniejszenie ilości węzłów z pięciu do trzech dałoby tylko sześć warunków nierównościowych, lecz (chyba) byłoby to wylanie dziecka razem z kąpielą.

Pora teraz na zastosowanie bliższe nurtowi (i nazwie) wykładu. Przez chwilę będzie znowu o modelach $\pm$ doskonale skorelowanych.

Czytelnik nabierze wprawy w posługiwaniu się Twierdzeniem 9.2, rozwiązując samodzielnie (względnie śledząc rozwiązanie ukryte pod dodatkowym kliknięciem) następujące proste

Ćwiczenie 10.1

W modelu $\pm$ doskonale skorelowanym z Przykładu 3.1 w Wykładzie III, w aspekcie M [z którym związany jest Rysunek 3.2; w Wykładzie III jeszcze nie znaliśmy aspektu B] znaleźć wszystkie portfele minimalnego ryzyka, przy czym specjalnie stosując w tym celu Twierdzenie 9.2.

Wskazówka:

Chodzi o minimalizację wariancji portfela $x\in\Delta^{4}$ , która w tym modelu $\pm$ doskonale skorelowanym wyraża się, jeśli pamiętamy to jeszcze z Wykładu III, wzorem $(4x_{1}+x_{2}-x_{3}-4x_{4})^{2}$ . To minimum jest bardzo łatwo znaleźć tak po prostu, przy czym osiągane jest ono w punktach przecięcia płaszczyzny krytycznej z sympleksem $\Delta^{4}$ (porównaj Przykład 6.2). Teraz chodzi nam o uzyskanie tego samego jeszcze raz, wprost z twierdzenia K-KT.

Rozwiązanie:

Po odpowiednim wyspecyfikowaniu Twierdzenia 9.2, zresztą bardzo podobnym do tego, które rozwijane jest niżej w tym wykładzie w kontekście relatywnego minimum ryzyka, szukamy portfeli $x=(x_{1},\, x_{2},\, x_{3},\, x_{4})^{{\text{T}}}\in\Delta^{4}$ , dla których istnieje $\lambda=\lambda(x)\in\mathbb{R}$ takie, że: po pierwsze (używając nie całej, tylko połowy wariancji)

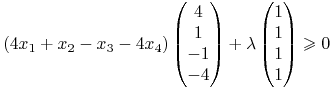$(4x_{1}+x_{2}-x_{3}-4x_{4})\begin{pmatrix}4\\ 1\\ -1\\ -4\end{pmatrix}+\lambda\begin{pmatrix}1\\ 1\\ 1\\ 1\end{pmatrix}\ge 0$

(10.1)

jako wektor w $\mathbb{R}^{4}$ (= nieujemność każdej składowej wektora po lewej stronie), oraz, po drugie, iloczyn skalarny wektora stojącego po lewej stronie (10.1) z wektorem $x$ jest zero:

$(4x_{1}+x_{2}-x_{3}-4x_{4})^{2}+\lambda=0$

(10.2)

(warunek komplementarności przy przyjętej specyfikacji twierdzenia). Dodajmy teraz stronami na przykład dwie środkowe nierówności w (10.1).²⁷albo dwie skrajne, albo wszystkie cztery Dostajemy nieujemność współczynnika $\lambda$ . Lecz (10.2) daje niedodatniość $\lambda$ . Zatem $\lambda=0$ , więc też, znowu z (10.2), $4x_{1}+x_{2}-x_{3}-4x_{4}=0$ . Ryzyko w aspekcie M minimalizują więc te portfele Markowitza, które … mają zerowe ryzyko. (Porównaj też jeszcze raz Przykład 6.2.) Niby nic, lecz ,,wycisnęliśmy tę” informację z Twierdzenia 9.2!

Już w tym rozwiązaniu wychodzą cechy charakterystyczne twierdzenia K-KT. Po bliższym przyjrzeniu się okazuje się, że jedna część jego tezy, tu zapisana jako (10.1), ciągnie niejako szukany współczynnik Lagrange'a (w ćwiczeniu jest on tylko jeden) w jedną stronę. Natomiast druga część tezy, tu (10.2), ciągnie ten współczynnik w drugą stronę. W efekcie wyłania się jakaś równowagowa wartość takiego współczynnika, która de facto jest zakodowanym opisem ekstremów. Nie przypadkiem w literaturze francuskojęzycznej, np w [25], twierdzenie K-KT jest nazywane twierdzeniem o punkcie siodłowym.

Ćwiczenie 10.2

Znaleźć przy pomocy Twierdzenia 9.2 wszystkie portfele minimalnego ryzyka w aspekcie M w dowolnym modelu $\pm$ doskonale skorelowanym.

Naszym głównym celem w Wykładzie X jest zastosowanie Twierdzenia Karusha-Kuhna-Tuckera 9.2 (w przyszłości będziemy już pisać tylko krótko `K-KT') do zautomatyzowanego poszukiwania portfeli relatywnie minimalnego ryzyka w modelach Markowitza, które bliższe są warunkom giełdowym niż modele $\pm$ doskonale skorelowane.

Dla (niezdegenerowanych) modeli Blacka w Wykładzie VI polegało to na dość standardowym zastosowaniu wiedzy z AM II, bo dwa warunki ograniczające były tylko równościowe. W efekcie gładko dostaliśmy (w Twierdzeniu 6.1) wszystkie portfele krytyczne Blacka układające się na prostej krytycznej Blacka.

Teraz jednak dochodzi $k$ ograniczeń nierównościowych związanych z leżeniem portfeli w sympleksie $\Delta^{k}$ (nieujemność składowych portfeli, brak krótkiej sprzedaży), co komplikuje sytuację. Jest to jakościowo nowy problem. Czym teraz zastąpiona zostanie prosta krytyczna Blacka?

Zgodnie z tradycją przyjętą w analizie portfelowej, współczynniki Lagrange'a związane z warunkami równościowymi $e^{{\text{T}}}x=1$ , $\mu^{{\text{T}}}x=E$ (wartości $E$ nie będą teraz dowolne, tylko ograniczone do powłoki wypukłej wartości oczekiwanych stóp zwrotu ze spółek numer $1,\, 2,\dots,\, k$ ) piszemy jako, odpowiednio, $\lambda$ i $-\lambda _{E}$ , zaś nierówności $x_{i}\ge 0$ ( $i=1,\, 2,\dots,\, k$ ) kodujemy jako $a_{{i+2}}^{{\text{T}}}x\le b_{{i+2}}$ , gdzie $a_{{i+2}}=[0,\dots,\underset{\underset{i}{\uparrow}}{-1},\dots,\, 0]^{{\text{T}}}$ , $b_{{i+2}}=0$ , $i=1,\, 2,\dots,\, k$ . Jako funkcję $f$ bierzemy

$f(y)=\frac{1}{2}y^{{\text{T}}}\Sigma\, y,\quad y\in G=\mathbb{R}^{k},$

która dla $\Sigma\ge 0$ jest wypukła i różniczkowalna w każdym punkcie $y$ , zaś jej gradient to $\nabla f(y)=\Sigma y$ . Twierdzenie K-KT zastosowane w tej sytuacji mówi, że $x$ spełniający wymienione warunki jest globalnym minimum $f$ przy podanych warunkach (ograniczeniach) $\Longleftrightarrow$ istnieją $\lambda,\lambda _{E}\in\mathbb{R}$ takie, że

$\Sigma x+\lambda e-\lambda _{E}\mu\ge 0\ \text{ jako wektor w }\mathbb{R}^{k}\ \ \underline{\text{oraz}}\ \ x^{{\text{T}}}(\Sigma x+\lambda e-\lambda _{E}\mu)=0\ (\text{warunek komplementarności})\,.$

Podamy teraz warunek dostateczny, przy którym takie portfele relatywnie minimalnego ryzyka istnieją i są jednoznacznie wyznaczone dla każdej wartości $E\in[\underset{1\le i\le k}{\min}\mu _{i},\,\underset{1\le i\le k}{\max}\mu _{i}]$ . Jest on trochę za silny (mógłby być trochę osłabiony), co w praktyce jednak nie przeszkadza, bo przy estymacji wartości oczekiwanych z historycznych danych giełdowych praktycznie nigdy nie dostaniemy pary równych wartości. W zamian zaś pozwala zręcznie opisać procedurę poszukiwania.

Mianowicie, w dalszym ciągu zakładamy, że $\Sigma>0$ oraz

$\ne\big(\mu _{1},\,\mu _{2},\dots,\,\mu _{k}\big)\,$

(10.3)

tzn. wszystkie wartości oczekiwane $\mu _{i}$ są różne. Te założenia będą obowiązywać do odwołania. (Zauważamy, że są to silniejsze założenia niż dawna informacja (5.2), która wystarczała w teorii Blacka. Przy różnych pod-zestawach zmiennych będziemy w obecnym algorytmie wracać do (5.2).)

Algorytm prowadzący do rozwiązania nie mówi od razu, dla jakich konkretnie wartości $E$ rozwiązanie znajdziemy na konkretnej ścianie sympleksu. Całość poszukiwań dzielimy (niestety lub stety) na etapy, których jest

$\binom{k}{0}+\binom{k}{1}+\binom{k}{2}+\cdots+\binom{k}{k-2}\,=\, 2^{k}-k-1\,.$

(10.4)

Etap $\emptyset$ . Szukanie wśród portfeli $x\in\Delta^{k}\colon x_{1}>0,\,\, x_{2}>0,\,\dots,\, x_{k}>0$ .
Warunek komplementarności pociąga wtedy wektorową równość

$\Sigma x+\lambda e-\lambda _{E}\mu\,=\, 0,$

co łącznie z dwoma ograniczeniami równościowymi w problemie zapisujemy przy pomocy tzw. macierzy Lagrange'a, tu wymiaru $k+2$ :

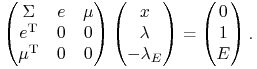$\begin{pmatrix}\Sigma&e&\mu\\ e^{{\text{T}}}&0&0\\ \mu^{{\text{T}}}&0&0\end{pmatrix}\begin{pmatrix}x\\ \lambda\\ -\lambda _{E}\end{pmatrix}=\begin{pmatrix}0\\ 1\\ E\end{pmatrix}.$

Dawne założenie (5.2) oczywiście wynika z (10.3), więc dostajemy tu jedyne rozwiązanie $(x,\,\lambda,\,\lambda _{E})(E)$ , na temat którego rozwiązujemy następnie układ nierówności $x_{1}(E)>0,\,\, x_{2}(E)>0,\,\dots,\,\, x_{k}(E)>0$ . Wynikiem jest jakiś przedział otwarty wartości $E$ (być może pusty) i odpowiadające portfele $x(E)$ . Macierz Lagrange'a, która tu została przywołana i użyta, to tylko przeformułowanie i pewne uzwarcenie metody Blacka i noblistów z Wykładu VI. Portfele $x(E)$ ewentualnie wyłaniające się w tym etapie są tożsame z portfelami Blacka (6.2) z Wykładu VI leżącymi wewnątrz sympleksu $\Delta^{k}$ . Na dalszych etapach tak już być nie musi (i najczęściej nie będzie); jednak patrz też Ćwiczenia 11.1 i 11.2 oraz Uwaga 11.2 w Wykładzie XI. Uzwarcenie metody dawane przez macierz Lagrange'a będzie nam pomocne w dalszych etapach.
Wreszcie nazwa tego etapu, $\emptyset$ , oznacza, że pusty jest w nim zbiór indeksów zmiennych, które przyjmujemy za zero.

Ogólniej, etap OUT, gdzie $\text{OUT}\subset\{ 1,\, 2,\dots,\, k\}$ , $0\le\#(\text{OUT})\le k-2$ , polega na szukaniu
$x\in\Delta^{k}\colon x_{j}=0$ dla $j\in\text{OUT}$ , natomiast $x_{i}>0$ dla $i\in\text{IN}\overset{\text{def}}{=}\{ 1,\, 2,\dots,\, k\}\,\,\backslash\,\,\text{OUT}$ , spełniających warunki w omawianej tu wersji twierdzenia K-KT, tzn.

$(\Sigma x+\lambda e-\lambda _{E}\mu)_{i}=0\ \text{ dla }\ i\in\text{IN},\qquad(\Sigma x+\lambda e-\lambda _{E}\mu)_{i}\ge 0\ \text{dla }\ i\in\text{OUT}$

(10.5)

dla jakichś $\lambda,\,\lambda _{E}\in\mathbb{R}$ . Równości w (10.5) wynikają z warunku komplementarności, zaś nierówności w (10.5) wynikają z warunku na gradient minimalizowanej funkcji. Oznacza to konkretnie, że w takim etapie OUT najpierw rozwiązujemy układ $2+\#(\text{IN})\ge 2+2=4$ równań liniowych

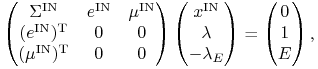$\begin{pmatrix}\Sigma^{{\text{IN}}}&e^{{\text{IN}}}&\mu^{{\text{IN}}}\\ (e^{{\text{IN}}})^{{\text{T}}}&0&0\\ (\mu^{{\text{IN}}})^{{\text{T}}}&0&0\end{pmatrix}\begin{pmatrix}x^{{\text{IN}}}\\ \lambda\\ -\lambda _{E}\end{pmatrix}=\begin{pmatrix}0\\ 1\\ E\end{pmatrix},$

(10.6)

gdzie $\Sigma^{{\text{IN}}}$ to macierz $\Sigma$ po wyrzuceniu wierszy i kolumn o numerach z OUT oraz $e^{{\text{IN}}}$ , $\mu^{{\text{IN}}}$ to wektory $e,\,\mu$ po odrzuceniu składowych o numerach z OUT.

Ważne jest, że $\Sigma^{{\text{IN}}}>0$ oraz $\mu^{{\text{IN}}}\nparallel e^{{\text{IN}}}$ , a więc stosuje się teoria Blacka i współautorów, tyle, że w wymiarze $\#(\text{IN})$ , nie zaś $k$ . Tu właśnie pracuje zestaw założeń (10.3), $\Sigma>0$ i $\#(\text{IN})\ge 2$ .

Ćwiczenie 10.3

Uzasadnić, że istotnie, założenia $\Sigma>0$ i $\#(\text{IN})\ge 2$ pociągają $\Sigma^{{\text{IN}}}>0$ .

Uzasadnić też, że założenia (10.3) i $\#(\text{IN})\ge 2$ pociągają $\mu^{{\text{IN}}}\nparallel e^{{\text{IN}}}$ .

Tym sposobem wiemy, że rozwiązania $(x^{{\text{IN}}},\,\lambda,\,\lambda _{E})(E)$ układu (10.6) istnieją i są jedyne. Z pomocą przyszedł nam, dosyć niespodziewanie, Wykład VI.
Mając już te rozwiązania, rozwiązujemy następnie ze względu na $E$ układ nierówności

$\left\{\begin{array}[]{ll}x_{i}(E)>0,&\hbox{$i\in\text{IN}$,}\\ \big(\Sigma x(E)+\lambda(E)e-\lambda _{E}(E)\mu\big)_{j}\ge 0,&\hbox{$j\in\text{OUT}$.}\end{array}\right.$

W wyniku otrzymujemy przecięcie $k$ półprostych domkniętych i/lub otwartych, czyli, ogólnie rzecz biorąc, przedział postaci $(\ )$ , lub $(\ \,]$ , lub $[\ \,)$ , lub $[\ \,\,]$ , albo też $\emptyset$ .

Definicja 10.1

Przedział ten będziemy w dalszym ciągu nazywać $E(\text{IN})$ ; uprości nam to w przyszłości przedstawienie kluczowego dla tych wykładów Algorytmu Prostej Krytycznej (skrót nazwy angielskiej, nieomalże powszechnie przyjętej, to: CLA).

Tak przebiegamy wszystkie $2^{k}-k-1$ etapów, w których $\#(\text{IN})\ge 2$ . (Przypominamy, że takie ograniczenie z dołu na liczebność zbiorów IN było ważne i gwarantowało, oczywiście przy założeniu (10.3), nierównoległość zredukowanych wektorów $\mu^{{\text{IN}}}$ oraz $e^{{\text{IN}}}$ , a w efekcie możliwość stosowania na każdym etapie OUT klasycznej teorii Blacka i współautorów.)

Przykład 10.1 (ważny; wracamy do niego już po raz czwarty, za każdym razem w innym kontekście, po Wykładach: V (Przykład 5.2), VII (Ćwiczenie 7.3) i IX (Przykład 9.1))

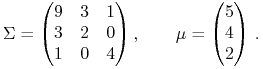$\Sigma=\begin{pmatrix}9&3&1\\ 3&2&0\\ 1&0&4\end{pmatrix},\qquad\mu=\begin{pmatrix}5\\ 4\\ 2\end{pmatrix}\,.$

Etap $\text{OUT}=\emptyset$ . Nieostre nierówności stają się (warunek komplementarności!) równościami – w tym etapie szukamy ewentualnych punktów prostej krytycznej leżących wewnątrz sympleksu standardowego. Rozwiązujemy zatem równanie (patrz Twierdzenie 5.1)

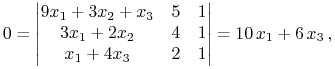$0=\begin{vmatrix}9x_{1}+3x_{2}+x_{3}&5&1\\ 3x_{1}+2x_{2}&4&1\\ x_{1}+4x_{3}&2&1\end{vmatrix}=10\, x_{1}+6\, x_{3}\,,$

oczywiście z zerowym skutkiem. Ten etap nic nie daje, bo prosta krytyczna nie przechodzi tu przez wnętrze sympleksu: $E(\{ 1,\, 2,\, 3\})=\emptyset$ .²⁸Zamiast liczyć wyznacznik, można sobie przypomnieć, że prosta krytyczna muska tylko trójkąt w wierzchołku $e_{2}$ – patrz pierwszy z filmików w Wykładzie V.

Etap $\text{OUT}=\{ 1\}$ , w którym $x_{1}=0$ , $x_{2}>0$ , $x_{3}>0$ . Piszemy odpowiedni układ równań (10.6)

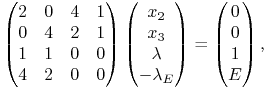$\begin{pmatrix}2&0&4&1\\ 0&4&2&1\\ 1&1&0&0\\ 4&2&0&0\end{pmatrix}\begin{pmatrix}x_{2}\\ x_{3}\\ \lambda\\ -\lambda _{E}\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 1\\ E\end{pmatrix},$

którego rozwiązania to

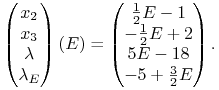$\begin{pmatrix}x_{2}\\ x_{3}\\ \lambda\\ \lambda _{E}\end{pmatrix}(E)=\begin{pmatrix}\frac{1}{2}E-1\\ -\frac{1}{2}E+2\\ 5E-18\\ -5+\frac{3}{2}E\end{pmatrix}.$

Dodatniość $x_{2}$ i $x_{3}$ oznacza, że $E\in(2,\, 4)$ . Co teraz z pierwszą nierównością $3x_{2}+x_{3}+\lambda-5\lambda _{E}\ge 0$ , która też musi być spełniona przez portfele relatywnie minimalnego ryzyka? Po podstawieniu rozwiązań jest to nierówność $4\ge E$ , spełniona przez $E$ ze wskazanego przedziału otwartego. Wniosek: $E(\{ 2,\, 3\})=(2,\, 4)$ .

Etap $\text{OUT}=\{ 2\}$ , w którym $x_{1}>0$ , $x_{2}=0$ , $x_{3}>0$ . Odpowiedni układ równań (10.6) to teraz

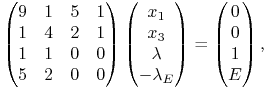$\begin{pmatrix}9&1&5&1\\ 1&4&2&1\\ 1&1&0&0\\ 5&2&0&0\end{pmatrix}\begin{pmatrix}x_{1}\\ x_{3}\\ \lambda\\ -\lambda _{E}\end{pmatrix}=\begin{pmatrix}0\\ 0\\ 1\\ E\end{pmatrix},$

którego rozwiązania to z kolei

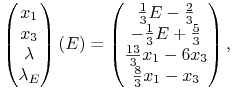$\begin{pmatrix}x_{1}\\ x_{3}\\ \lambda\\ \lambda _{E}\end{pmatrix}(E)=\begin{pmatrix}\frac{1}{3}E-\frac{2}{3}\\ -\frac{1}{3}E+\frac{5}{3}\\ \frac{13}{3}x_{1}-6x_{3}\\ \frac{8}{3}x_{1}-x_{3}\end{pmatrix},$

gdzie celowo $\lambda$ i $\lambda _{E}$ zostały uzależnione `tylko' od $x_{1},\, x_{3}$ . Dodatniość $x_{1}$ i $x_{3}$ oznacza, że $E\in(2,\, 5)$ . Co tym razem z drugą nierównością $3x_{1}+\lambda-4\lambda _{E}\ge 0$ ? Po podstawieniu rozwiązań jej lewa strona to $-\frac{10}{3}x_{1}-2x_{3}$ , a więc wielkość ujemna. Wniosek: $E(\{ 1,\, 3\})=\emptyset$ .

Jeśli chodzi o etap $\text{OUT}=\{ 3\}$ , to analogiczne rachunki dają w efekcie $E(\{ 1,\, 2\})=(4,\, 5)$ . Zatem, podsumowując, z całego przedziału $[E_{{\min}},\, E_{{\max}}]=[2,\, 5]$ dostajemy tutaj $(2,\, 4)\cup(4,\, 5)$ . Jest to cały $[E_{{\min}},\, E_{{\max}}]$ bez trzech węzłów wyróżnionych, w terminologii wprowadzanej w Twierdzeniu 10.1 na końcu tego wykładu.

Ćwiczenie 10.4

Skoro, w tym jednym modelu, dla wszystkich, lub prawie wszystkich wartości $E$ znaleźliśmy portfele relatywnie minimalnego ryzyka w aspekcie M, bez trudu możemy już wskazać portfele, które przechodzą na granicę minimalną $F_{{\min}}$ w tym modelu i aspekcie. Należy to zrobić teraz, po czym porównać odpowiedź z łamaną efektywną w tym samym modelu, będącą przedmiotem Ćwiczenia 7.3 w Wykładzie VII. Zbiór portfeli wyłaniający się z bieżącego ćwiczenia to przykład łamanej portfeli relatywnie minimalnego ryzyka ilustrujący Twierdzenie 10.1 poniżej.

Zanim sformułujemy zapowiadane twierdzenie ogólne, przyjrzymy się jeszcze autentycznie przełomowemu przykładowi modelu Markowitza w wymiarze 4, pochodzącemu od K. Więcha [29], w którym każdy etap OUT przynosi niepusty zbiór rozwiązań $E$ . Przykład ten był (tylko) anonsowany w Wykładzie VII. Mianowicie

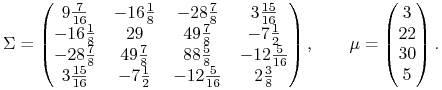$\Sigma=\begin{pmatrix}9\frac{7}{16}&-16\frac{1}{8}&-28\frac{7}{8}&3\frac{15}{16}\\ -16\frac{1}{8}&29&49\frac{7}{8}&-7\frac{1}{2}\\ -28\frac{7}{8}&49\frac{7}{8}&88\frac{5}{8}&-12\frac{5}{16}\\ 3\frac{15}{16}&-7\frac{1}{2}&-12\frac{5}{16}&2\frac{3}{8}\end{pmatrix},\qquad\mu=\begin{pmatrix}3\\ 22\\ 30\\ 5\end{pmatrix}.$

(10.7)

Wówczas po wykonaniu wszystkich $11=2^{4}-4-1$ etapów OUT uzyskuje się następujące rozwiązania:

Przedział wartości $E$	Skrajne wartości parametru $\lambda _{E}$	Etap OUT
$(3,\, 5)$	$\lambda _{E}(3+)=-\frac{11}{4}$	$\{ 2,3\}$
$(3,\, 5)$	$\lambda _{E}(5-)=-\frac{25}{32}$	$\{ 2,3\}$
$\left(5,\frac{38}{7}\right]$	$\lambda _{E}(5+)=-\frac{47}{80}$	$\{ 1,2\}$
$\left(5,\frac{38}{7}\right]$	$\lambda _{E}\left(\frac{38}{7}\right)=-\frac{1423}{2800}$	$\{ 1,2\}$
$\left(\frac{38}{7},\,\frac{6020}{1051}\right)$	$\lambda _{E}\left(\frac{6020}{1051}\right)=-\frac{1951}{4204}$	$\{ 1\}$
$\left[\frac{6020}{1051},\,\frac{8288}{1287}\right]$	$\lambda _{E}\left(\frac{8288}{1287}\right)=-\frac{1801}{5148}$	$\{ 1,3\}$
$\left(\frac{8288}{1287},\,\frac{73178}{9335}\right]$	$\lambda _{E}\left(\frac{73178}{9335}\right)=-\frac{13067}{74680}$	$\{ 3\}$
$\left(\frac{73178}{9335},\,\frac{10177}{1129}\right)$	$\lambda _{E}\left(\frac{10177}{1129}\right)=-\frac{941}{18064}$	$\emptyset$
$\left[\frac{10177}{1129},\,\frac{993}{101}\right)$	$\lambda _{E}\left(\frac{933}{101}\right)=\frac{599}{14544}$	$\{ 2\}$
$\left[\frac{993}{101},\,\frac{645}{64}\right]$	$\lambda _{E}\left(\frac{645}{64}\right)=\frac{865}{9216}$	$\{ 2,4\}$
$\left(\frac{645}{64},\,\frac{7499}{587}\right)$	$\lambda _{E}\left(\frac{7499}{587}\right)=\frac{5341}{9392}$	$\{ 4\}$
$\left[\frac{7499}{587},\, 22\right)$	$\lambda _{E}(22-)=\frac{19}{8}$	$\{ 3,4\}$
$(22,\, 30)$	$\lambda _{E}(22+)=\frac{167}{64}$	$\{ 1,4\}$
$(22,\, 30)$	$\lambda _{E}(30-)=\frac{155}{32}$	$\{ 1,4\}$

Nawet w tej chwili (w roku akademickim 2009/10) przykład ten wygląda wspaniale, a co dopiero w roku 2001, gdy się pojawił. Proszę np zwrócić uwagę, jaką formalną symetrię środkową ma ciąg typów przedziałów wartości $E$ w lewej kolumnie:

$(\ \ )\leftarrow(\ \ ]\leftarrow(\ \ )\leftarrow[\ \ ]\leftarrow(\ \ ]\leftarrow(\ \ )\rightarrow[\ \ )\rightarrow[\ \ ]\rightarrow(\ \ )\rightarrow[\ \ )\rightarrow(\ \ )\,.$

Ćwiczenie 10.5 (sprawdzające)

Narysować wykres funkcji

$(3,\, 30)\ni E\longmapsto\lambda _{E}(E)\,,$

której węzły wykresu są zakodowane w powyższej tabeli. (Pomiędzy węzłami, jak wynika z opisu etapów algorytmu, funkcja $\lambda _{E}$ jest liniowa. Ogólnie jest więc ona kawałkami liniowa.)

Rozwiązanie:

Zadanie to jest rozwiązane w ostatnim Wykładzie XV (Rysunek 15.2). Wszystkie dane do rysunku są jednak dostępne już teraz i każdy czytelnik może wykonać własną wersję wykresu.

Ogólne twierdzenie na temat zbiorów portfeli relatywnie minimalnego ryzyka w modelach Markowitza musi … poczekać jeszcze chwilę, bo właśnie teraz nadarza się najlepsza okazja, by ugruntować jednocześnie i model Więcha i twierdzenie K-KT.
Portfeli minimalnego ryzyka szukaliśmy dotąd przy pomocy tego twierdzenia w modelach $\pm$ doskonale skorelowanych (Ćwiczenia 10.1 i 10.2 powyżej). Natomiast w modelach niezdegenerowanych – jak ten koronny przykład Więcha – jeszcze nie.

Ćwiczenie 10.6

W modelu Więcha znaleźć, oczywiście w aspekcie M, portfel $\widetilde{x}_{{\min}}$ o najmniejszej wariancji. (Jest to równocześnie, warto wiedzieć, portfel efektywny w aspekcie M o najmniejszej wartości oczekiwanej; więcej o tych sprawach będzie w Wykładzie XI.)

Wskazówka:

Zastosować algorytm bazujący na twierdzeniu K-KT, tym razem z jednym ograniczeniem równościowym $e^{{\text{T}}}x=1$ zamiast dwóch i z czterema ograniczeniami nierównościowymi $x_{i}\ge 0$ , $i=1,\, 2,\, 3,\, 4$ .

Rozwiązanie:

Inne niż sugerowane we wskazówce rozwiązanie, mniej eleganckie (zo to wykorzystujące Tabelę powyżej), jest podane w Przykładzie 11.2.

Twierdzenie 10.1 (nt zbioru portfeli relatywnie minimalnego ryzyka w modelach Markowitza)

$\bullet$ Przy założeniach $\Sigma>0$ oraz (10.3), portfele relatywnie minimalnego ryzyka w modelu Markowitza tworzą łamaną Ł o nie więcej niż $2^{k}-k-1$ rozłącznych bokach. Każdy bok jest odcinkiem $(\ )$ lub $(\ \,]$ lub $[\ \,)$ lub $[\ \,\,]$ , i każdy leży w innej ścianie sympleksu $\Delta^{k}$ (będącej krawędzią, bądź trójkątem, bądź czworościanem, bądź …, bądź wnętrzem $\Delta^{k}$ ). Portfele na różnych bokach Ł mają więc różne składy jakościowe, a na danym boku niezmienny skład jakościowy.

$\bullet\bullet$ Nie wszystkie końce boków łamanej Ł należą do Ł. Takich wyróżnionych przez nienależenie wierzchołków Ł zawsze jest nie mniej niż dwa i nie więcej niż $k$ – są to niektóre z wierzchołków sympleksu $\Delta^{k}$ , przy czym zawsze – wierzchołki o najmniejszej i największej wartości oczekiwanej. Te wyróżnione wierzchołki łamanej Ł odpowiadają wartościom parametru $E\in\left[\underset{1\le i\le k}{\min}(\mu _{i}),\,\underset{1\le i\le k}{\max}(\mu _{i})\right]$ , które pozostają nieobsłużone po wykonaniu wszystkich $2^{k}-k-1$ etapów OUT dla $\text{OUT}\subset\{ 1,\, 2,\dots,\, k\}$ , $\#\text{OUT}\le k-2$ . Takie wartości $E$ nazywamy węzłami wyróżnionymi.

$\bullet\bullet\bullet$ Po domknięciu w wierzchołkach wyróżnionych łamana $\overline{\text{Ł}}$ jest łamaną spójną. Ł, czy też częściej $\overline{\text{Ł}}$ , jest nazywana łamaną wierzchołkową w danym modelu Markowitza (dużo rzadziej nazywa się ją ”łamaną portfeli relatywnie minimalnego ryzyka”).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Analiza Portfelowa i Rynki Kapitałowe 1

10. Wykład X, 4.XII.2009

Ćwiczenie 10.1

Ćwiczenie 10.2

Ćwiczenie 10.3

Definicja 10.1

Przykład 10.1 (ważny; wracamy do niego już po raz czwarty, za każdym razem w innym kontekście, po Wykładach: V (Przykład 5.2), VII (Ćwiczenie 7.3) i IX (Przykład 9.1))

Ćwiczenie 10.4

Ćwiczenie 10.5 (sprawdzające)

Ćwiczenie 10.6

Twierdzenie 10.1 (nt zbioru portfeli relatywnie minimalnego ryzyka w modelach Markowitza)