11. Wykład XI, 11.XII.2009
Dowodzimy teraz Twierdzenia 10.1, jednego z kilku najważniejszych w wykładach z APRK1.
Zgodnie z algorytmem opisanym w Wykładzie X, wykonujemy
wszystkie ![]() etapów szukania rozwiązań problemu
portfeli relatywnie minimalnego ryzyka, indeksowanych podzbiorami
etapów szukania rozwiązań problemu
portfeli relatywnie minimalnego ryzyka, indeksowanych podzbiorami
![]() ,
, ![]() .29Czasem,
szczególnie gdy wymiar
.29Czasem,
szczególnie gdy wymiar ![]() jest 3 lub 4, wygodniej jest indeksować uzupełniającymi
zbiorami OUT; najzwyklejsze przejście do uzupełnień w zbiorze
wszystkich indeksów. W danym etapie IN, dla
jest 3 lub 4, wygodniej jest indeksować uzupełniającymi
zbiorami OUT; najzwyklejsze przejście do uzupełnień w zbiorze
wszystkich indeksów. W danym etapie IN, dla ![]() [przedział – patrz Definicja 10.1 w Wykładzie X – który
może też być pusty; wtedy nic w takim etapie IN nie dostajemy]
otrzymujemy jednoznacznie wyznaczony portfel
[przedział – patrz Definicja 10.1 w Wykładzie X – który
może też być pusty; wtedy nic w takim etapie IN nie dostajemy]
otrzymujemy jednoznacznie wyznaczony portfel ![]() leżący na ścianie IN,
przy czym przyporządkowanie
leżący na ścianie IN,
przy czym przyporządkowanie ![]() jest liniowe.
jest liniowe.
W tym momencie portfel ![]() nie jest jeszcze zdefiniowany dla
jakiejkolwiek wartości
nie jest jeszcze zdefiniowany dla
jakiejkolwiek wartości ![]() , która nie wyłania się
z algorytmu w Wykładzie X, a są takie – będziemy mieli tego
przykłady, patrz część
, która nie wyłania się
z algorytmu w Wykładzie X, a są takie – będziemy mieli tego
przykłady, patrz część ![]() w twierdzeniu.
Remedium na to jest proste:
w twierdzeniu.
Remedium na to jest proste:
-
a) funkcja
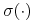 osiąga minimum na zbiorze
osiąga minimum na zbiorze
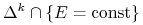 ,
, ![E\in[E_{{\min}},\, E_{{\max}}]](wyklady/pk1/mi/mi1262.png) ,
,
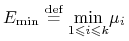 ,
,
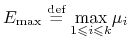 (jako funkcja ciągła na zbiorze zwartym) oraz
(jako funkcja ciągła na zbiorze zwartym) oraz
-
b) punkt realizujący to minimum jest jedyny, gdyż
 jest
ściśle wypukła (patrz Ćwiczenie 6.4 w Wykładzie VI;
argumenty nie muszą być zawężane do sympleksu
jest
ściśle wypukła (patrz Ćwiczenie 6.4 w Wykładzie VI;
argumenty nie muszą być zawężane do sympleksu 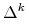 ,
mogłyby też być z całej przestrzeni
,
mogłyby też być z całej przestrzeni 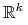 ), więc zawsze, na przykład,
), więc zawsze, na przykład,
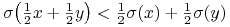 dla
dla 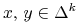 ,
, 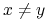 . (Dwa różne portfele
minimalizujące ryzyko przy tej samej wartości oczekiwanej
produkowałyby trzeci portfel o tej samej wartości
oczekiwanej i mniejszym ryzyku.)
. (Dwa różne portfele
minimalizujące ryzyko przy tej samej wartości oczekiwanej
produkowałyby trzeci portfel o tej samej wartości
oczekiwanej i mniejszym ryzyku.)
Ten jedyny punkt wymieniony w b) i dotyczący danej wartości
![]() nazywamy
nazywamy ![]() . Nie wywołuje to
kolizji z poprzednio nadanymi nazwami: dla wartości
. Nie wywołuje to
kolizji z poprzednio nadanymi nazwami: dla wartości ![]() wyłaniających
się z algorytmu w Wykładzie X, odrobinę starszy
wyłaniających
się z algorytmu w Wykładzie X, odrobinę starszy ![]() i teraz
nowy
i teraz
nowy ![]() to jeden i ten sam portfel leżący w
to jeden i ten sam portfel leżący w ![]() .30W istocie
do jedynego portfela
.30W istocie
do jedynego portfela ![]() wygenerowanego w punkcie b) powyżej dochodzi się
przy słabszych założeniach, niż w Twierdzeniu 10.1.
Wystarczałoby tylko
wygenerowanego w punkcie b) powyżej dochodzi się
przy słabszych założeniach, niż w Twierdzeniu 10.1.
Wystarczałoby tylko ![]() , dające ścisłą wypukłość funkcji ryzyka.
Nawet w zupełnie skrajnym wypadku
, dające ścisłą wypukłość funkcji ryzyka.
Nawet w zupełnie skrajnym wypadku ![]() ,
gdy dziedzina rozważanej funkcji ryzyka kurczy się do punktu. Tylko
wtedy …. jest bardzo mało interesujących wartości
,
gdy dziedzina rozważanej funkcji ryzyka kurczy się do punktu. Tylko
wtedy …. jest bardzo mało interesujących wartości ![]() – tylko
jedna, więc też w ogóle tylko jeden portfel
– tylko
jedna, więc też w ogóle tylko jeden portfel ![]() .
.
Uwaga terminologiczna jest taka, że portfel Markowitza ![]() ,,prawie zawsze” jest czymś innym niż portfel Blacka
,,prawie zawsze” jest czymś innym niż portfel Blacka ![]() ,
(6.2), z Twierdzenia 6.1 w Wykładzie VI,
i nowe oznaczenie ma o tym przypominać. Czasem jednak
,
(6.2), z Twierdzenia 6.1 w Wykładzie VI,
i nowe oznaczenie ma o tym przypominać. Czasem jednak ![]() może być portfelem
może być portfelem ![]() ; na przykład wtedy,
gdy początkowy etap
; na przykład wtedy,
gdy początkowy etap ![]() w algorytmie wnosi niepusty
wkład do zbioru portfeli relatywnie minimalnego ryzyka.
Można to łatwo doprecyzować:
w algorytmie wnosi niepusty
wkład do zbioru portfeli relatywnie minimalnego ryzyka.
Można to łatwo doprecyzować:
Ćwiczenie 11.1
Uzasadnić, że ![]() .
.
W sytuacji jak w tym ćwiczeniu, dany portfel relatywnie
minimalnego ryzyka ma po prostu dwie nazwy: starą ![]() z Wykładu VI i nową
z Wykładu VI i nową ![]() z bieżącego wykładu.
z bieżącego wykładu.
Wracając do meritum dowodu Twierdzenia 10.1, podstawowym
pytaniem jest, czy przedziały ![]() są, dla różnych
zbiorów IN, parami rozłączne.
są, dla różnych
zbiorów IN, parami rozłączne.
Odpowiedź brzmi: tak, właśnie z powodu jednoznaczności
rozwiązań problemu portfeli relatywnie minimalnego ryzyka.
![]() dla
dla
![]() , bo rozwiązanie, będąc
jedynym, nie może leżeć na dwu różnych ścianach.
, bo rozwiązanie, będąc
jedynym, nie może leżeć na dwu różnych ścianach.
Wobec tego ![]() to cały przedział
to cały przedział ![]() z wyjątkiem co najwyżej
z wyjątkiem co najwyżej ![]() wartości odpowiadających zbiorom IN
jednoelementowym, dla których opisana metoda znajdowania portfela
wartości odpowiadających zbiorom IN
jednoelementowym, dla których opisana metoda znajdowania portfela
![]() nie działa (lecz gdzie rozwiązania wcale nie muszą trafiać).
nie działa (lecz gdzie rozwiązania wcale nie muszą trafiać).
Istotnie, na jakimkolwiek poziomie ![]() odpowiadające mu jedyne rozwiązanie
odpowiadające mu jedyne rozwiązanie ![]() musi leżeć na jakiejś
ścianie sympleksu, i nie można wykluczyć, że jest to ściana
0-wymiarowa. Jeśli rzeczywiście jakiś wierzchołek
musi leżeć na jakiejś
ścianie sympleksu, i nie można wykluczyć, że jest to ściana
0-wymiarowa. Jeśli rzeczywiście jakiś wierzchołek ![]() (
(![]() ), to takiej wartości
), to takiej wartości ![]() nie uzyskuje się z algorytmu.
nie uzyskuje się z algorytmu.
Liczby ze zbioru ![]() to właśnie węzły wyróżnione z treści twierdzenia.31Że
nie muszą to być wszystkie
to właśnie węzły wyróżnione z treści twierdzenia.31Że
nie muszą to być wszystkie ![]() wartości
wartości ![]() , pokazuje przykład:
, pokazuje przykład:
![]() , w którym
, w którym ![]() ,
,
![]() ,
, ![]() ,
,
![]() , a zatem węzły wyróżnione to tylko
, a zatem węzły wyróżnione to tylko ![]() oraz
oraz ![]() .
.
Widać też, że ![]() oraz
oraz ![]() zawsze są węzłami wyróżnionymi:
dla jakiejkolwiek co najmniej 1-wymiarowej ściany IN (tj
zawsze są węzłami wyróżnionymi:
dla jakiejkolwiek co najmniej 1-wymiarowej ściany IN (tj ![]() )
przedział
)
przedział ![]() jest – przy założeniu (10.3) –
rozłączny z kresami dolnym i górnym wartości parametru
jest – przy założeniu (10.3) –
rozłączny z kresami dolnym i górnym wartości parametru ![]() na tej ścianie,
więc na pewno rozłączny z liczbami
na tej ścianie,
więc na pewno rozłączny z liczbami ![]() oraz
oraz ![]() .
.
Natomiast węzły niewyróżnione to, z definicji, wszystkie te
wartości ![]() , które są końcami jakichś
przedziałów
, które są końcami jakichś
przedziałów ![]() ,
, ![]() , uwaga:
leżącymi w
, uwaga:
leżącymi w ![]() .
.
Definiujemy teraz łamaną Ł jako
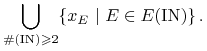 |
Jest to suma nie więcej niż ![]() rozłącznych odcinków
różnych typów na końcach:
rozłącznych odcinków
różnych typów na końcach: ![]() ,
, ![]() ,
, ![]() lub
lub ![]() .
Jak są one położone względem siebie w
.
Jak są one położone względem siebie w ![]() ? Dlaczego Ł,
po domknięciu, jest spójną łamaną?
? Dlaczego Ł,
po domknięciu, jest spójną łamaną?
Niech, dla ustalenia uwagi, ![]() i albo
i albo ![]() – węzeł wyróżniony z podchodzącym
do niego z lewej przedziałem
– węzeł wyróżniony z podchodzącym
do niego z lewej przedziałem ![]() , przy czym oczywiście
, przy czym oczywiście
![]() ; np
; np ![]() w przykładzie Więcha, kiedy to
w przykładzie Więcha, kiedy to ![]() oraz
oraz ![]() .
.
Albo też![]() – węzeł niewyróżniony z
podchodzącym do niego z lewej przedziałem
– węzeł niewyróżniony z
podchodzącym do niego z lewej przedziałem ![]() .
(W tym drugim przypadku oczywiście
.
(W tym drugim przypadku oczywiście ![]() i
i ![]() już z konieczności należy do odpowiedniego przedziału
już z konieczności należy do odpowiedniego przedziału ![]() podchodzącego do
podchodzącego do ![]() z prawej.) Np
z prawej.) Np ![]() w przykładzie Więcha, kiedy to
w przykładzie Więcha, kiedy to ![]() oraz
oraz ![]() .
.
Pokażemy, że w każdym przypadku portfele ![]() dążą
do
dążą
do ![]() gdy
gdy ![]() ,
co już da potrzebną ciągłość łamanej wierzchołkowej Ł.
,
co już da potrzebną ciągłość łamanej wierzchołkowej Ł.
Dla ![]() trochę mniejszych niż
trochę mniejszych niż ![]() portfele
portfele ![]() leżą na ścianie
leżą na ścianie ![]() i mamy konkretne, afiniczne
względem
i mamy konkretne, afiniczne
względem ![]() , wzory na
, wzory na ![]() ,
, ![]() ,
, ![]() .
Niech
.
Niech
Oczywiście ![]() ,
, ![]() ,
,
![]() , przy czym
, przy czym
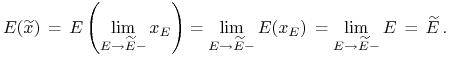 |
Portfele relatywnie minimalnego ryzyka ![]() dla
dla
![]() spełniały warunki dawane przez
twierdzenie K-T:
spełniały warunki dawane przez
twierdzenie K-T:
| (11.1) |
Przechodząc w (11.1) z ![]() do
do ![]() ,
mamy oczywiście
,
mamy oczywiście
![\left\{\begin{array}[]{ll}\Sigma\widetilde{x}+\widetilde{\lambda}e-\widetilde{\lambda}_{E}\mu\ge 0\,,&\\
\widetilde{x}^{{\text{T}}}\Big(\Sigma\widetilde{x}+\widetilde{\lambda}e-\widetilde{\lambda}\mu\Big)=0\,.&\end{array}\right.](wyklady/pk1/mi/mi1197.png) |
(11.2) |
Z twierdzenia K-KT, ![]() jest zatem
portfelem relatywnie minimalnego ryzyka w
jest zatem
portfelem relatywnie minimalnego ryzyka w ![]() mającym wartość oczekiwaną
mającym wartość oczekiwaną ![]() , czyli
, czyli
![]() .
Dowód twierdzenia jest zakończony.
.
Dowód twierdzenia jest zakończony.
Uwaga 11.1 (po dowodzie)
Uzyskane w tym dowodzie wartości współczynników Lagrange'a
![]() i
i ![]() nie muszą być
określone jednoznacznie. Są jednoznaczne dla wartości
nie muszą być
określone jednoznacznie. Są jednoznaczne dla wartości ![]() – węzłów niewyróżnionych (bo wtedy mamy jednoznaczność dla
– węzłów niewyróżnionych (bo wtedy mamy jednoznaczność dla
![]() na ścianie IN takiej, że
na ścianie IN takiej, że
![]() , i w
szczególności dla
, i w
szczególności dla ![]() ; patrz
też Wniosek 15.1 w Wykładzie XV).
; patrz
też Wniosek 15.1 w Wykładzie XV).
Nie muszą natomiast być jednoznaczne dla wartości ![]() – węzłów wyróżnionych, porównaj np różne granice jednostronne
współczynników
– węzłów wyróżnionych, porównaj np różne granice jednostronne
współczynników ![]() w
w ![]() lub 22 w
przykładzie Więcha. (Patrz też Wniosek 15.2 w
Wykładzie XV.)
lub 22 w
przykładzie Więcha. (Patrz też Wniosek 15.2 w
Wykładzie XV.)
Uwaga 11.2
W warunkach Twierdzenia 10.1 mamy jednoznaczność łamanej
wierzchołkowej Ł. Możemy oglądać dosyć imponujące przykłady łamanych:
na Rysunku 7.5 w Wykładzie VII (złożona tylko z portfeli efektywnych,
więc tożsama z łamaną efektywną), czy na Rysunku 15.1 w Wykładzie XV
(ilustrującym przykład Więcha). Trzeba jednak pamiętać, że tę jednoznaczność
mamy przy założeniach Twierdzenia 10.1. Gdy macierz
kowariancji jest tylko nieujemnie określona, wtedy może zatracać się
jednoznaczność spójnej łamanej obsługującej – po obłożeniu odwzorowaniem
![]() – całą granicę
– całą granicę ![]() w aspekcie M.
w aspekcie M.
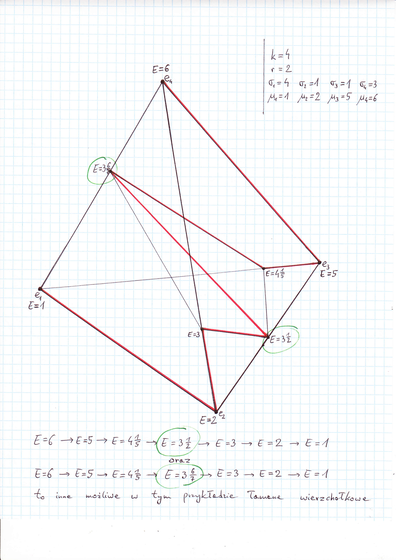
Dla przykładu, oto rysunek sympleksu ![]() , który należy
oglądać razem z Rysunkiem 3.3 w Wykładzie III. Jedną z takich
możliwych łamanych jest łamana narysowana tu na czerwono (ma ona
7 boków). Niżej na rysunku wskazane są dwie inne (każda z nich
ma 6 boków). Możliwa jest jeszcze inna łamana, najprostsza z
nich wszystkich, mająca 5 boków:
, który należy
oglądać razem z Rysunkiem 3.3 w Wykładzie III. Jedną z takich
możliwych łamanych jest łamana narysowana tu na czerwono (ma ona
7 boków). Niżej na rysunku wskazane są dwie inne (każda z nich
ma 6 boków). Możliwa jest jeszcze inna łamana, najprostsza z
nich wszystkich, mająca 5 boków:
![]() .
.
[W wersji pdf rysunek nie mieści się tutaj, za to otwiera następną stronę.]
Tym samym mamy już przykład, gdy po osłabieniu założeń Twierdzenia 10.1
zatraca się jednoznaczność łamanej Ł. Trzeba jednak też wspomnieć,
że jednoznaczna łamana Ł obsługująca ![]() może istnieć
i przy osłabionych założeniach. Już Przykład 4.2 w Wykładzie IV
był/jest taki! Jednoznaczna łamana w nim to
może istnieć
i przy osłabionych założeniach. Już Przykład 4.2 w Wykładzie IV
był/jest taki! Jednoznaczna łamana w nim to ![]() ; patrz też dolna część Rysunku 4.6
w Wykładzie IV.
; patrz też dolna część Rysunku 4.6
w Wykładzie IV.
Ćwiczenie 11.2
Dla portfeli relatywnie minimalnego ryzyka położonych na boku
![]() łamanej implicite
obecnej w Przykładach 4.2 i 7.1, a więc portfeli spełniających w szczególności
odpowiednie warunki K-KT przy relatywnej minimalizacji ryzyka portfeli Markowitza,
znaleźć wszystkie możliwe wartości współczynnika Lagrange'a
łamanej implicite
obecnej w Przykładach 4.2 i 7.1, a więc portfeli spełniających w szczególności
odpowiednie warunki K-KT przy relatywnej minimalizacji ryzyka portfeli Markowitza,
znaleźć wszystkie możliwe wartości współczynnika Lagrange'a ![]() we
wspomnianych warunkach K-KT.
we
wspomnianych warunkach K-KT.
Z opisu łamanej widzimy, że w ćwiczeniu chodzi o etap ![]() .
Wspomniany bok łamanej jest rozwiązaniem – wkładem tego właśnie etapu do całej
konstrukcji łamanej. Bierzemy dowolny punkt
.
Wspomniany bok łamanej jest rozwiązaniem – wkładem tego właśnie etapu do całej
konstrukcji łamanej. Bierzemy dowolny punkt ![]() z tego boku. Układ równań
z tego boku. Układ równań
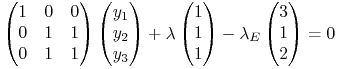 |
ma więc, przy jakichś współczynnikach ![]() i
i ![]() , rozwiązanie
(i to w liczbach dodatnich, co bez znaczenia). Zatem rząd macierzy tego
układu równań liniowych i rząd macierzy rozszerzonej o kolumnę wyrazów
wolnych – są równe (twierdzenie Kroneckera-Capellego):
, rozwiązanie
(i to w liczbach dodatnich, co bez znaczenia). Zatem rząd macierzy tego
układu równań liniowych i rząd macierzy rozszerzonej o kolumnę wyrazów
wolnych – są równe (twierdzenie Kroneckera-Capellego):
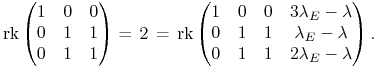 |
Stąd ![]() , czyli
, czyli ![]() .
We wszystkich portfelach na tym boku warunki K-T wymuszają jedną jedyną
wartość
.
We wszystkich portfelach na tym boku warunki K-T wymuszają jedną jedyną
wartość ![]() (mimo, że portfele te, jak wiemy, nie są efektywne
w aspekcie M).
(mimo, że portfele te, jak wiemy, nie są efektywne
w aspekcie M).
Uwaga 11.3
Łamana wierzchołkowa jest zbudowana z portfeli ![]() . W zasadzie
wiemy już, z Ćwiczenia 11.2 powyżej, kiedy
. W zasadzie
wiemy już, z Ćwiczenia 11.2 powyżej, kiedy ![]() . Jednak tamta
wiedza jest mało operatywna: co to znaczy, że
. Jednak tamta
wiedza jest mało operatywna: co to znaczy, że ![]() ?
Nie należy sądzić, że jest tak tylko wtedy, gdy prosta krytyczna
Blacka idzie przez wnętrze sympleksu
?
Nie należy sądzić, że jest tak tylko wtedy, gdy prosta krytyczna
Blacka idzie przez wnętrze sympleksu ![]() , względnie gdy
muska jeden z wierzchołków
, względnie gdy
muska jeden z wierzchołków ![]() . Prosta krytyczna może
przecież nie spotykać wnętrza całego sympleksu, tylko wnętrze
jakiejś mniej-wymiarowej jego ściany! Przykład takiej sytuacji
jest w ćwiczeniu tu poniżej.
. Prosta krytyczna może
przecież nie spotykać wnętrza całego sympleksu, tylko wnętrze
jakiejś mniej-wymiarowej jego ściany! Przykład takiej sytuacji
jest w ćwiczeniu tu poniżej.
Ćwiczenie 11.3
W jednym z klasycznych przykładów używanych do ilustrowania wykładów z APRK1,
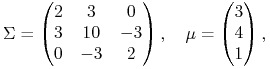 |
prosta krytyczna Blacka trafia w portfel ![]() , przez który
wchodzi do wnętrza trójkąta
, przez który
wchodzi do wnętrza trójkąta ![]() , po czym wychodzi zeń
przez wnętrze ściany
, po czym wychodzi zeń
przez wnętrze ściany ![]() . Zmienić wartość
współczynnika
. Zmienić wartość
współczynnika ![]() na taką, by prosta krytyczna w zmienionym modelu zawierała bok
na taką, by prosta krytyczna w zmienionym modelu zawierała bok
![]() .32ma to związek z zadaniem
na egzaminie z APRK1 na Wydziale MIM UW w III.2009
.32ma to związek z zadaniem
na egzaminie z APRK1 na Wydziale MIM UW w III.2009
Szukamy – Twierdzenie 5.1 w Wykładzie V –
wartości ![]() takiej, by portfel
takiej, by portfel ![]() był krytyczny, tzn.
by trzeci wiersz macierzy kowariancji był liniowo zależny od
wektorów
był krytyczny, tzn.
by trzeci wiersz macierzy kowariancji był liniowo zależny od
wektorów ![]() oraz
oraz ![]() :
:
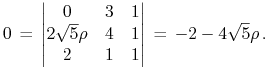 |
Stąd ![]() .
(Nie zapominamy też sprawdzić, czy w ogóle dostajemy wtedy
macierz przydatną w analizie portfelowej – tu owszem, tak.
Tą odpowiedzią w ćwiczeniu jest
.
(Nie zapominamy też sprawdzić, czy w ogóle dostajemy wtedy
macierz przydatną w analizie portfelowej – tu owszem, tak.
Tą odpowiedzią w ćwiczeniu jest ![]() .)
.)
Przykłady węzłów wyróżnionych i niewyróżnionych w łamanych wierzchołkowych w Twierdzeniu 10.1.
-
a) Dla przykładu pojawiającego się w Ćwiczeniu 11.3 powyżej jeszcze przed zmianą współczynnika korelacji
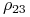 ,
,
![E\big(\{ 2,\, 3\}\big)=(1,\, 2]](wyklady/pk1/mi/mi1212.png) ,
, 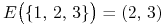 ,
,
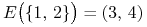 ,
, 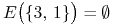 .
Zatem wszystkie trzy wartości oczekiwane
.
Zatem wszystkie trzy wartości oczekiwane 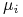 są węzłami
wyróżnionymi, natomiast wartość 2 jest węzłem niewyróżnionym.
są węzłami
wyróżnionymi, natomiast wartość 2 jest węzłem niewyróżnionym.
-
b) Dla Przykładu 4.1 w Wykładzie IV, bardzo dobrze wtedy rozpracowanego (patrz też Rysunek 4.7),
![E\big(\{ 2,3\}\big)=(1,\,\frac{4}{3}]](wyklady/pk1/mi/mi1288.png) ,
,
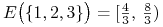 ,
, 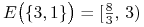 ,
,
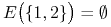 . Zatem węzły wyróżnione to tylko
. Zatem węzły wyróżnione to tylko
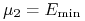 oraz
oraz 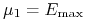 . Dochodzą do nich jeszcze
dwa węzły niewyróżnione
. Dochodzą do nich jeszcze
dwa węzły niewyróżnione 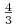 i
i 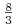 .
.
Stwierdzenie 11.1
W modelu Markowitza ![]() ,
, ![]() , spełniającym założenie
(10.3), funkcja
, spełniającym założenie
(10.3), funkcja ![]() jest ściśle wypukła.
jest ściśle wypukła.
Niech ![]() , obie wartości wzięte ze wskazanego przedziału, oraz
, obie wartości wzięte ze wskazanego przedziału, oraz
![]() ,
, ![]() . Wtedy wystarczy porównać ryzyka portfeli
. Wtedy wystarczy porównać ryzyka portfeli
![]() oraz
oraz ![]() , z których drugi też leży w
, z których drugi też leży w
![]() i ma taką samą wartość oczekiwaną
i ma taką samą wartość oczekiwaną ![]() jak pierwszy.
Z definicji pierwszego portfela mamy pierwszą (nieostrą) nierówność w
jak pierwszy.
Z definicji pierwszego portfela mamy pierwszą (nieostrą) nierówność w
zaś druga (ostra) nierówność spowodowana jest ścisłą wypukłością
funkcji ![]() , już dobrze
znaną z Ćwiczenia 6.4 (Wykład VI).
, już dobrze
znaną z Ćwiczenia 6.4 (Wykład VI).
Założenie (10.3) w Stwierdzeniu 11.1 jest nadmiarowe – porównaj wcześniej w tym wykładzie przypis nr 2; w wersji html – przypis nr 30. Jest ono jednak eksponowane celowo dla utrzymania przejrzystości całej sytuacji, ponieważ pojawiło się już w Twierdzeniu 10.1, pomagając uprościć jego [niedawno przeprowadzony] dowód.
Wniosek 11.1
Przy tych samych założeniach co w Stwierdzeniu 11.1, również
funkcja ![]() jest
ściśle wypukła.
jest
ściśle wypukła.
Istotnie, jest to złożenie funkcji ściśle wypukłej ze Stwierdzenia 11.1
z funkcją ![]() , która jest rosnąca i ściśle wypukła na dodatniej
półosi prostej rzeczywistej.
, która jest rosnąca i ściśle wypukła na dodatniej
półosi prostej rzeczywistej.
Stwierdzenie 11.2
Przy założeniu ![]() , w aspekcie M istnieje jeden
jedyny portfel
, w aspekcie M istnieje jeden
jedyny portfel ![]() minimalizujący ryzyko wśród wszystkich
portfeli Markowitza. Oznaczamy go
minimalizujący ryzyko wśród wszystkich
portfeli Markowitza. Oznaczamy go ![]() .
.
Istotnie. Jego istnienie wynika z twierdzenia Weierstrassa. Jego jedyność wynika ze ścisłej wypukłości ryzyka portfeli przy dodatniej macierzy kowariancji.
Przykład 11.1
W przykładzie Więcha w Wykładzie X już znaleźliśmy (my = ci, którzy
wykonali Ćwiczenie 10.6) taki portfel ![]() , drogą
,,przeczesania” wielu etapów przy sprawdzaniu warunków K-KT.
, drogą
,,przeczesania” wielu etapów przy sprawdzaniu warunków K-KT.
Teraz, w sytuacji ogólnej, będziemy używać tego samego symbolu na
portfel o najmniejszym ryzyku w aspekcie M: ![]() .
.
Obserwacja. 11.1 Funkcja
![]() jest ściśle rosnąca.
jest ściśle rosnąca.
Przedział ![]() jest maksymalnym przedziałem rosnącości funkcji
jest maksymalnym przedziałem rosnącości funkcji
![]() .
.
Istotnie, punkt ![]() jest punktem
globalnego minimum funkcji ze Stwierdzenia 11.1. Funkcja
ściśle wypukła, poczynając od miejsca swojego globalnego minimum,
jest ściśle rosnąca. Przy tym maksymalność podanego przedziału
jest od razu widoczna.
jest punktem
globalnego minimum funkcji ze Stwierdzenia 11.1. Funkcja
ściśle wypukła, poczynając od miejsca swojego globalnego minimum,
jest ściśle rosnąca. Przy tym maksymalność podanego przedziału
jest od razu widoczna.
Stwierdzenie 11.3
(a) Przy założeniu ![]() portfel
portfel ![]() jest
zawsze efektywny w aspekcie M.
jest
zawsze efektywny w aspekcie M.
(b) Przy założeniach ![]() i (10.3), portfele efektywne
w aspekcie M to spójna część łamanej
i (10.3), portfele efektywne
w aspekcie M to spójna część łamanej ![]() zaczynająca się w
zaczynająca się w ![]() i kończąca się w
i kończąca się w ![]() .
.
Dowód (a). Gdyby punkt ![]() leżał w cieniu jakiegoś punktu
leżał w cieniu jakiegoś punktu ![]() ,
, ![]() ,
to byłoby
,
to byłoby
przy czym co najmniej jedna z tych nierówności byłaby ostra. Jednak
pierwsza nierówność jest tu z konieczności równością ![]() , i to równością ryzyk dwóch różnych
portfeli. W takiej sytuacji średnia arytmetyczna tych portfeli,
również leżąca w
, i to równością ryzyk dwóch różnych
portfeli. W takiej sytuacji średnia arytmetyczna tych portfeli,
również leżąca w ![]() , miałaby ryzyko mniejsze od minimalnego
możliwego, sprzeczność. (Drugiej nieostrej nierówności w ogóle
tu nie użyliśmy.)
, miałaby ryzyko mniejsze od minimalnego
możliwego, sprzeczność. (Drugiej nieostrej nierówności w ogóle
tu nie użyliśmy.)
Dowód (b).
Portfele ![]() dla
dla ![]() są oczywiście zdominowane przez
są oczywiście zdominowane przez ![]() , bo
, bo
![]() . Nie są więc efektywne
(patrz specyfikacja po ogólnej Definicji 7.2 w Wykładzie VII).
. Nie są więc efektywne
(patrz specyfikacja po ogólnej Definicji 7.2 w Wykładzie VII).
Co dla ![]() ? Gdyby jakiś portfel
? Gdyby jakiś portfel
![]() dominował wtedy portfel
dominował wtedy portfel ![]() , tzn. byłoby
, tzn. byłoby
| (11.3) |
i co najmniej jedna z tych nierówności była ostra, to:
-
gdyby to pierwsza nierówność w (11.3) była ostra, wtedy, używając drugiej nierówności w (11.3) oraz Obserwacji 11.1, mielibyśmy
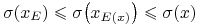 ,33druga
w tym ciągu nierówności dlatego, że portfele
,33druga
w tym ciągu nierówności dlatego, że portfele 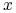 oraz
oraz 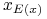 mają
tę samą wartość oczekiwaną
mają
tę samą wartość oczekiwaną 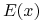 , zaś portfel
, zaś portfel 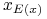 minimalizuje
ryzyko przy ustalonej wartości oczekiwanej
minimalizuje
ryzyko przy ustalonej wartości oczekiwanej 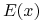 a więc dokładnie
przeciwnie, niż mówi pierwsza (teraz, pamiętamy, ostra) nierówność
w (11.3).
a więc dokładnie
przeciwnie, niż mówi pierwsza (teraz, pamiętamy, ostra) nierówność
w (11.3).
Stąd wniosek, że hipotetyczny portfel ![]() dominujący portfel
dominujący portfel
![]() nie istnieje, więc ten ostatni jest efektywny (jeszcze
raz Definicja 7.2 i jej specyfikacja).
nie istnieje, więc ten ostatni jest efektywny (jeszcze
raz Definicja 7.2 i jej specyfikacja).
Definicja 11.1
Część łamanej wierzchołkowej ![]() , złożoną z portfeli
efektywnych w aspekcie M i dokładnie opisaną w Stwierdzeniu 11.3,
nazywamy łamaną efektywną. Jest to domknięta i spójna część łamanej
, złożoną z portfeli
efektywnych w aspekcie M i dokładnie opisaną w Stwierdzeniu 11.3,
nazywamy łamaną efektywną. Jest to domknięta i spójna część łamanej
![]() – jej [chciałoby się powiedzieć] podłamana.
– jej [chciałoby się powiedzieć] podłamana.
Teraz już innymi oczami odczytujemy hasło pod Rysunkiem 7.5 w Wykładzie VII. Inaczej też zapewne odbieramy garść informacji historycznych podaną na końcu tamtego Wykładu VII.
Jak szukać łamanych efektywnych? W praktyce konkretnie i skutecznie
szuka się łamanej efektywnej [w danym modelu spełniającym założenia
Twierdzenia 10.1] analizując wszystkie funkcje
![]() uzyskiwane na kolejnych etapach algorytmu szukania
łamanej wierzchołkowej podanego na Wykładzie X. Trzeba tylko wyrazić
rosnącość ściśle wypukłej funkcji
uzyskiwane na kolejnych etapach algorytmu szukania
łamanej wierzchołkowej podanego na Wykładzie X. Trzeba tylko wyrazić
rosnącość ściśle wypukłej funkcji ![]() na maksymalnym możliwym
przedziale, uchwyconą w Obserwacji 11.1, przez znak jej pochodnej –
w punktach (prawie wszystkich), gdzie jest różniczkowalna. Pomocna
w tym będzie, oczywiście, Obserwacja 6.1 z Wykładu VI.
na maksymalnym możliwym
przedziale, uchwyconą w Obserwacji 11.1, przez znak jej pochodnej –
w punktach (prawie wszystkich), gdzie jest różniczkowalna. Pomocna
w tym będzie, oczywiście, Obserwacja 6.1 z Wykładu VI.
Na jej podstawie, w punktach wewnętrznych wszystkich niepustych
przedziałów ![]() , czyli we wszystkich punktach
, czyli we wszystkich punktach ![]() przedziału
przedziału
![]() bez co najwyżej
bez co najwyżej ![]() punktów, funkcja
punktów, funkcja
![]() jest różniczkowalna i jej pochodna wynosi
jest różniczkowalna i jej pochodna wynosi ![]() ,
gdzie
,
gdzie ![]() wzięta jest z teorii Blacka na odpowiednim
przedziale
wzięta jest z teorii Blacka na odpowiednim
przedziale ![]() .
.![]() Jeśli w jakimś takim punkcie odpowiednia funkcja
Jeśli w jakimś takim punkcie odpowiednia funkcja
![]() ma miejsce zerowe, wtedy portfel
ma miejsce zerowe, wtedy portfel ![]() rozpoczynający łamaną efektywną, a więc i cała ta łamana, są już
znalezione.
rozpoczynający łamaną efektywną, a więc i cała ta łamana, są już
znalezione.![]() Jeśli nie, to jeden z węzłów (nie wiemy w tej chwili:
wyróżniony czy niewyróżniony, w tym momencie nie ma to znaczenia)
rozgranicza znaki funkcyj
Jeśli nie, to jeden z węzłów (nie wiemy w tej chwili:
wyróżniony czy niewyróżniony, w tym momencie nie ma to znaczenia)
rozgranicza znaki funkcyj ![]() : na lewo od niego
odpowiednie funkcje obcięte do wnętrz przedziałów
: na lewo od niego
odpowiednie funkcje obcięte do wnętrz przedziałów ![]() są ujemne, zaś na prawo od niego są dodatnie. Od tego więc węzła
aż do
są ujemne, zaś na prawo od niego są dodatnie. Od tego więc węzła
aż do ![]() rozciąga się maksymalny przedział rosnącości funkcji
rozciąga się maksymalny przedział rosnącości funkcji
![]() , czyli łamana efektywna zaczyna się w punkcie (portfelu)
, czyli łamana efektywna zaczyna się w punkcie (portfelu)
![]() .
.
Poniżej (Przykład 11.2) prześledzimy te stwierdzenia na koronnym dla
nas przykładzie Więcha podanym w Wykładzie X. Na jego temat jest tam
dokładna Tabela z wszystkimi funkcjami ![]() wraz z ich
dziedzinami.
wraz z ich
dziedzinami.
Uwaga 11.4
Czytelnik ma prawo zapytać, co dzieje się z różniczkowalnością funkcji
![]() w węzłach, wyróżnionych i niewyróżnionych, których –
jak wiemy – łącznie jest zawsze nie więcej niż
w węzłach, wyróżnionych i niewyróżnionych, których –
jak wiemy – łącznie jest zawsze nie więcej niż ![]() ? Wyczerpujące
odpowiedzi będą podane w Wykładzie XV w sekcji `Uzasadnienie poprawności
algorytmu CLA'. Różniczkowalność okaże się mieć miejsce
zawsze w węzłach niewyróżnionych (Wniosek 15.1).
Zaś węzły wyróżnione w Wykładzie XV okażą się być rzędnymi
punktów, w których granica minimalna w aspekcie M – przy
warunkach niezdegenerowania przyjmowanych w algorytmie CLA – ma
punkty załamania (kinki, Wniosek 15.2).
? Wyczerpujące
odpowiedzi będą podane w Wykładzie XV w sekcji `Uzasadnienie poprawności
algorytmu CLA'. Różniczkowalność okaże się mieć miejsce
zawsze w węzłach niewyróżnionych (Wniosek 15.1).
Zaś węzły wyróżnione w Wykładzie XV okażą się być rzędnymi
punktów, w których granica minimalna w aspekcie M – przy
warunkach niezdegenerowania przyjmowanych w algorytmie CLA – ma
punkty załamania (kinki, Wniosek 15.2).
Natomiast przy ogólnych założeniach Twierdzenia 10.1 mogą
też pojawiać się węzły wyróżnione niedające załamań granicy
minimalnej: węzły wyróżnione – punkty gładkości. W Ćwiczeniu 11.3
wcześniej w bieżącym wykładzie podany już był przykład takiej patologii:
przed zmianą współczynnika ![]() , wartość
, wartość ![]() jest
tam węzłem wyróżnionym i też rzędną punktu gładkości na
jest
tam węzłem wyróżnionym i też rzędną punktu gładkości na ![]() .
I także po zmianie wartości
.
I także po zmianie wartości ![]() węzeł
węzeł ![]() pozostaje
wyróżniony i gładki!34Nasuwa się pytanie, co dzieje się
z tym węzłem w tak zwanym międzyczasie – ?
pozostaje
wyróżniony i gładki!34Nasuwa się pytanie, co dzieje się
z tym węzłem w tak zwanym międzyczasie – ?
Przykład 11.2
Możliwe jest inne (przynajmniej formalnie; tak, czy inaczej posługujemy
się funkcjami ![]() pochodzącymi z zastosowań twierdzenia K-KT)
rozwiązanie Ćwiczenia 10.6 z Wykładu X. Operujemy już teraz bogatszą
terminologią pochodzącą z Twierdzenia 10.1 i z bieżącego wykładu:
pochodzącymi z zastosowań twierdzenia K-KT)
rozwiązanie Ćwiczenia 10.6 z Wykładu X. Operujemy już teraz bogatszą
terminologią pochodzącą z Twierdzenia 10.1 i z bieżącego wykładu:
Łamana efektywna w łamanej Ł zaczyna się na ścianie ![]() ,
gdyż podczas etapu
,
gdyż podczas etapu ![]() odpowiednia funkcja
odpowiednia funkcja ![]() zmienia znak w punkcie wewnętrznym przedziału
zmienia znak w punkcie wewnętrznym przedziału ![]() – patrz
właśnie Tabela w Wykładzie X. (Innymi słowy, z dwu możliwości
– patrz
właśnie Tabela w Wykładzie X. (Innymi słowy, z dwu możliwości ![]() i
i ![]() wydzielonych powyżej, zachodzi ta pierwsza.) Z podanych
w Tabeli skrajnych argumentów i wartości
wydzielonych powyżej, zachodzi ta pierwsza.) Z podanych
w Tabeli skrajnych argumentów i wartości ![]() w tym etapie
znajdujemy miejsce zerowe
w tym etapie
znajdujemy miejsce zerowe ![]() .
Tę wartość
.
Tę wartość ![]() podstawiamy do prostej krytycznej ściany
podstawiamy do prostej krytycznej ściany ![]() :
:
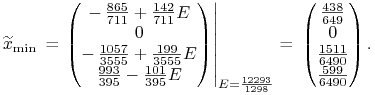 |
Ćwiczenie 11.4
Narysować łamaną efektywną w przykładzie Więcha.
Spojrzeć na Rysunek 15.1, trzymając w ręku Przykład 11.2.
Łamana wierzchołkowa to – w pierwotnej teorii Markowitza – odpowiednik prostej krytycznej Blacka. Może ona być naprawdę skomplikowana; wskazywaliśmy już odpowiednie rysunki uzasadniające tę tezę. W wykładach, dosyć paradoksalnie, najpierw poznaje się prostą Blacka, zaś łamaną wierzchołkową – będącą powrotem do źródeł teorii portfelowej! – dopiero poźniej.
Natomiast łamana efektywna to, oczywiście, odpowiednik półprostej
efektywnej Blacka, takiej jak np pokazana na Rysunku 7.6 w Wykładzie VII.
Jest ona obiektem dość finezyjnym, budowanym w oparciu o dość subtelne
pojęcie efektywności portfela. Czasem potrafi być nawet całą łamaną
wierzchołkową (jak na Rysunku 7.5 w przykładzie Krzyżewskiego),
czasem tylko jednym portfelem ![]() , np gdy
, np gdy
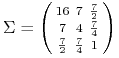 ,
, ![]() .35Mniejsza
już być nie może: portfel
.35Mniejsza
już być nie może: portfel ![]() zawsze jest efektywny w
aspekcie M. No i otwarte pozostaje ,,Ćwiczenie” 7.5 …
zawsze jest efektywny w
aspekcie M. No i otwarte pozostaje ,,Ćwiczenie” 7.5 …
Poznaliśmy już zmodyfikowany model Tobina (Black ![]() ”
”![]() ”),
zaś teraz poznamy oryginalny model Tobina: dołączenie banku
oferującego bezryzykowną stopę zwrotu
”),
zaś teraz poznamy oryginalny model Tobina: dołączenie banku
oferującego bezryzykowną stopę zwrotu ![]() (obowiązującą w obie
strony, pracownicy banku żywią się powietrzem) do podstawowego
modelu Markowitza.
(obowiązującą w obie
strony, pracownicy banku żywią się powietrzem) do podstawowego
modelu Markowitza.
Jeśli inwestor mający ![]() środków własnych dopożycza jeszcze
środków własnych dopożycza jeszcze
![]() środków z banku, wtedy przeznacza na zakup akcji
środków z banku, wtedy przeznacza na zakup akcji
![]() i jego bilans budżetowy to
i jego bilans budżetowy to
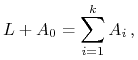 |
(11.4) |
gdzie ![]() to kwota, za którą kupuje akcje spółki nr
to kwota, za którą kupuje akcje spółki nr ![]() . Jeśli
zaś kwotę
. Jeśli
zaś kwotę ![]() wziętą ze swojego kapitału
wziętą ze swojego kapitału ![]() lokuje on w banku,
natomiast za resztę kupuje akcje spółek, wtedy jego bilans wygląda
lokuje on w banku,
natomiast za resztę kupuje akcje spółek, wtedy jego bilans wygląda
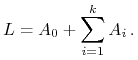 |
(11.5) |
Równania (11.4), (11.5) zapisujemy przejrzyściej w postaci
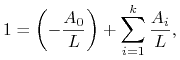 |
(11.6) |
względnie
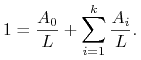 |
(11.7) |
W sytuacji (11.6) oznaczamy ![]() , zaś w
sytuacji (11.7)
, zaś w
sytuacji (11.7) ![]() . Ponadto kładziemy
. Ponadto kładziemy
![]() ,
, ![]() i w ten sposób portfele
w modelu Tobina to
i w ten sposób portfele
w modelu Tobina to ![]() -tki
-tki ![]() ,
w których
,
w których
Ujemne ![]() , porównaj (11.6), oznaczają dopożyczanie środków
w banku, natomiast dodatnie nieprzekraczające jedynki
, porównaj (11.6), oznaczają dopożyczanie środków
w banku, natomiast dodatnie nieprzekraczające jedynki ![]() , porównaj
(11.7), oznaczają lokowanie [części] własnych środków w banku.
, porównaj
(11.7), oznaczają lokowanie [części] własnych środków w banku.
Jaki zbiór tworzą tutaj portfele dopuszczalne ![]() ?
W zmodyfikowanym modelu Tobina w Wykładzie VIII była to, jak pamiętamy,
hiperpłaszczyzna
?
W zmodyfikowanym modelu Tobina w Wykładzie VIII była to, jak pamiętamy,
hiperpłaszczyzna ![]() , a teraz? Patrząc na opis powyżej,
widać od razu, że ten zbiór to
, a teraz? Patrząc na opis powyżej,
widać od razu, że ten zbiór to
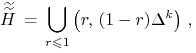 |
(11.8) |
a więc pewien nieograniczony stożek w ![]() zbudowany nad
sympleksem
zbudowany nad
sympleksem ![]() , czyli pewien nieograniczony
wielowymiarowy (dokładnie:
, czyli pewien nieograniczony
wielowymiarowy (dokładnie: ![]() -wymiarowy) hiper-ostrosłup.
-wymiarowy) hiper-ostrosłup.
Teoria opisująca ten model jest częściowo podobna do teorii Tobina
w sytuacji Blacka. Tamta prowadziła do pojęcia portfela ![]() optymalnego w modelu Blacka ze względu na panującą stopę bezryzykowną
optymalnego w modelu Blacka ze względu na panującą stopę bezryzykowną ![]() .
Ta obecna prowadzi do pojęcia portfela
.
Ta obecna prowadzi do pojęcia portfela ![]() optymalnego
w modelu Markowitza ze względu na panującą stopę bezryzykowną
optymalnego
w modelu Markowitza ze względu na panującą stopę bezryzykowną ![]() ,
,
tzn. maksymalizującego wśród portfeli ![]() współczynnik
Sharpe'a
współczynnik
Sharpe'a ![]() (porównaj Wykład IX i też Wykład I), gdzie
teraz zakłada się jedynie, że
(porównaj Wykład IX i też Wykład I), gdzie
teraz zakłada się jedynie, że ![]() ;
; ![]() jest zdefiniowane na początku tego wykładu.
jest zdefiniowane na początku tego wykładu.
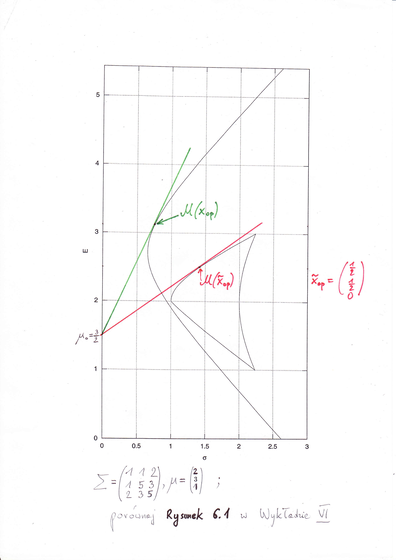
Różnica może być zasadnicza, bo [chciałoby się powiedzieć: tradycyjne] portfele Markowitza stanowią tylko drobną cząstkę wszystkich portfeli Blacka, i podobnie jest po przyłożeniu do portfeli mapy Markowitza. Niech za ilustrację posłuży następujący przykład [w wersji pdf rysunek przeskakuje na następną stronę]:
Maksima współczynników Sharpe'a w aspektach M i B różnią się, w tym przykładzie i przy tej stopie bezryzykownej, bardzo.
Ćwiczenie 11.5
Dla danych (6.1) użytych do wygenerowania Rysunku 11.2 powyżej
[w wersji pdf: poniżej], narysować zbiór osiągalny w modelu Tobina z tymi
właśnie parametrami, tzn. zbiór ![]() .
.
Użyć w tym celu informacji (11.8). Część pracy (rysowania zbioru osiągalnego) jest już na Rysunku 11.2 … wykonana.
Matematyczne instrumentarium prowadzące do opisu ![]() ,
znacznie finezyjniejsze niż w przypadku portfeli
,
znacznie finezyjniejsze niż w przypadku portfeli ![]() , będzie
przedstawione w końcowej części Wykładu XIII i na początku Wykładu XIV,
poprzez Twierdzenie 14.1, aż do Twierdzenia 14.2 włącznie.
W tej chwili podamy tylko motywację i sam goły wynik
– algorytm prowadzący do znalezienia
, będzie
przedstawione w końcowej części Wykładu XIII i na początku Wykładu XIV,
poprzez Twierdzenie 14.1, aż do Twierdzenia 14.2 włącznie.
W tej chwili podamy tylko motywację i sam goły wynik
– algorytm prowadzący do znalezienia ![]() .
.
Czy można jakoś ,,zgadnąć” taki algorytm, gdy chwilowo mamy
tylko wzór na portfel ![]() z Wykładu IX? Pytanie zaiste
karkołomne. Być może wzór zastąpić równaniem, bo przy rozgrywaniu
analogii [prosta Blacka versus łamana wierzchołkowa],
przed wzorem na portfele
z Wykładu IX? Pytanie zaiste
karkołomne. Być może wzór zastąpić równaniem, bo przy rozgrywaniu
analogii [prosta Blacka versus łamana wierzchołkowa],
przed wzorem na portfele ![]() mieliśmy równanie uwikłane na te
portfele, i właśnie tamto równanie zostało (dzięki czarodziejskiej
różdżce – Twierdzeniu 9.2) w coś przemienione.
mieliśmy równanie uwikłane na te
portfele, i właśnie tamto równanie zostało (dzięki czarodziejskiej
różdżce – Twierdzeniu 9.2) w coś przemienione.
Tak więc ![]() zapisujemy jako
zapisujemy jako ![]() ,
gdzie
,
gdzie ![]() , albo też
, albo też
| (11.9) |
To teraz spójrzmy z bliska na tamte równania uwikłane
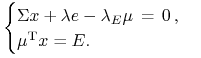 |
na portfel ![]() leżący w hiperpłaszczyźnie
leżący w hiperpłaszczyźnie ![]() .
.
I spójrzmy, co z nich zrobili czarodzieje K-KT:36nie dosłownie oni, lecz oni byli ,,ojcami założycielami”, patrz [12]
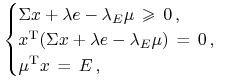 |
by znaleźć portfel ![]() . Równości
zamienili nierównościami i dla równowagi dodali warunek
komplementarności.
. Równości
zamienili nierównościami i dla równowagi dodali warunek
komplementarności.
Przypomnijmy jeszcze, że pierwszy problem rozwiązywał się
zupełnie standardowo (słynny układ dwóch równań liniowych o
niezerowym wyznaczniku), natomiast drugi – grając umiejętnie
nierównościami i komplementarnymi do nich równościami –
kawałkami sprowadzał się do pierwszego. Kawałkami ze względu
na wartości parametru ![]() . Takie spojrzenie na drugi problem
to właśnie wynik zastosowania twierdzenia K-KT.
. Takie spojrzenie na drugi problem
to właśnie wynik zastosowania twierdzenia K-KT.
Zaryzykujmy więc, chwyćmy różdżkę i przemieńmy (11.9) w … coś takiego
| (11.10) |
Tak jest, równości znowu zamienione nieostrymi nierównościami
i dla równowagi dodany warunek komplementarności …
Okaże się, że portfel ![]() istotnie jest
normalizacją rozwiązania (lub rozwiązań) problemu (11.10),
choć nie zawsze taki portfel będzie jedyny. Macierze
istotnie jest
normalizacją rozwiązania (lub rozwiązań) problemu (11.10),
choć nie zawsze taki portfel będzie jedyny. Macierze ![]() będą przy tym jak najbardziej dopuszczalne, choć w takich częściowo
zdegenerowanych sytuacjach sposób dochodzenia do
zagadnienia (11.10) będzie inny i delikatniejszy niż
gdy
będą przy tym jak najbardziej dopuszczalne, choć w takich częściowo
zdegenerowanych sytuacjach sposób dochodzenia do
zagadnienia (11.10) będzie inny i delikatniejszy niż
gdy ![]() . (Sam problem (11.10) czasami bywa nazywany
liniowym zagadnieniem komplementarności.)
. (Sam problem (11.10) czasami bywa nazywany
liniowym zagadnieniem komplementarności.)
W najciekawszych sytuacjach, gdy ![]() , na rozwiązanie będzie
się ,,polować” algorytmicznie i etapami, przez sprowadzanie
do (11.9), i następnie sprawdzanie znaków różnych wyrażeń,
umiejętnie grając na każdym etapie nierównościami i równoważącymi
je komplementarnymi równościami.
, na rozwiązanie będzie
się ,,polować” algorytmicznie i etapami, przez sprowadzanie
do (11.9), i następnie sprawdzanie znaków różnych wyrażeń,
umiejętnie grając na każdym etapie nierównościami i równoważącymi
je komplementarnymi równościami.
Trzeba będzie rozważać szerszą klasę funkcji niż tylko różniczkowalne
funkcje wklęsłe i wypukłe, która będzie dobrze pasować do współczynnika
Sharpe'a (czy raczej ten współczynnik do niej). Klasę jakby
stworzoną dla potrzeb analizy portfelowej,
Wystarczy już tej meta-analizy portfelowej. Chcemy wiedzieć, jak konkretnie rozwiązywać problem (11.10).
Zasadniczo – ten problem trzeba atakować w całości i próbować
wydobyć, czy wyłuskać z niego preportfel(e) ![]() i później dalej
– portfel(e)
i później dalej
– portfel(e) ![]() . Kłopotem jest możliwe
częściowe zdegenerowanie macierzy
. Kłopotem jest możliwe
częściowe zdegenerowanie macierzy ![]() ; Przykład 11.3 poniżej
jest na ten temat. Inny przypadek takiego całościowego szukania
rozwiązań (11.10), też przy zdegenerowanej macierzy
; Przykład 11.3 poniżej
jest na ten temat. Inny przypadek takiego całościowego szukania
rozwiązań (11.10), też przy zdegenerowanej macierzy ![]() ,
wystąpi potem w Ćwiczeniu 14.2, z kontunuacją też w Ćwiczeniu 14.3
(w Wykładzie XIV). Będzie to jednak już po zakończeniu dyskusji
poprawności (11.10).
,
wystąpi potem w Ćwiczeniu 14.2, z kontunuacją też w Ćwiczeniu 14.3
(w Wykładzie XIV). Będzie to jednak już po zakończeniu dyskusji
poprawności (11.10).
W międzyczasie, w sytuacji ![]() , przyjdzie nam wykonać w Wykładzie
XIV solidną pracę przygotowawczą. Chodzi o konstrukcję wypukłej dziedziny
dla pre-współczynnika Sharpe'a gdy
, przyjdzie nam wykonać w Wykładzie
XIV solidną pracę przygotowawczą. Chodzi o konstrukcję wypukłej dziedziny
dla pre-współczynnika Sharpe'a gdy ![]() (osobna sekcja w Wykładzie
XIV).37najwytrwalsi czytelnicy będą mieli satysfakcję estetyczną,
jak harmonijne jest tamto zastosowanie do analizy portfelowej funkcji
ogólniejszych niż wklęsłe różniczkowalne
(osobna sekcja w Wykładzie
XIV).37najwytrwalsi czytelnicy będą mieli satysfakcję estetyczną,
jak harmonijne jest tamto zastosowanie do analizy portfelowej funkcji
ogólniejszych niż wklęsłe różniczkowalne
Natomiast sytuacja będzie (i jest) dużo bardziej klarowna, gdy macierz
kowariancji ![]() jest dodatnio określona. Wtedy (pre)portfela
jest dodatnio określona. Wtedy (pre)portfela ![]() o nieujemnych składowych (lecz nie wszystkich równych zero!) szukać
będziemy etapami. Coś znaleźć musimy, bo portfel optymalny istnieje
z ogólnych powodów analityczno-topologicznych. Oto opis etapów
algorytmu.
o nieujemnych składowych (lecz nie wszystkich równych zero!) szukać
będziemy etapami. Coś znaleźć musimy, bo portfel optymalny istnieje
z ogólnych powodów analityczno-topologicznych. Oto opis etapów
algorytmu.
-
Etap
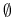 . Szukamy
. Szukamy 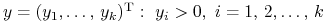 .
.
To oznacza (komplementarność!), że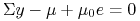 ,
albo, macierz
,
albo, macierz 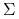 jest teraz odwracalna,
jest teraz odwracalna, 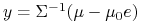 ,
dokładnie jak w zmodyfikowanym Tobinie. Teraz jednak musimy dodatkowo
sprawdzić, czy
,
dokładnie jak w zmodyfikowanym Tobinie. Teraz jednak musimy dodatkowo
sprawdzić, czy  . Jeśli tak, pre-portfel
. Jeśli tak, pre-portfel
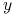 jest znaleziony. Jeśli nie, przechodzimy do
jest znaleziony. Jeśli nie, przechodzimy do
-
Etap 1. Szukamy
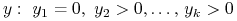 ,
a więc
,
a więc 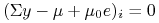 dla
dla 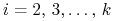 z warunku komplementarności, natomiast
z warunku komplementarności, natomiast 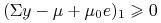 .
Rozwiązujemy ze względu na
.
Rozwiązujemy ze względu na 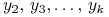 (można, bo wyznacznik
odpowiedniego układu
(można, bo wyznacznik
odpowiedniego układu 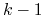 równań liniowych jest tutaj dodatni, a więc
różny od zera; patrz też niżej opis ogólnego etapu OUT), po czym sprawdzamy:
tutaj
równań liniowych jest tutaj dodatni, a więc
różny od zera; patrz też niżej opis ogólnego etapu OUT), po czym sprawdzamy:
tutaj 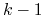 ostrych i jedną nieostrą nierówność. Spełnione lub nie;
w drugim przypadku przechodzimy do dalszych etapów.
ostrych i jedną nieostrą nierówność. Spełnione lub nie;
w drugim przypadku przechodzimy do dalszych etapów.Spróbujmy te potencjalnie możliwe dalsze etapy opisać łącznie, podobnie jak to już zrobiliśmy przy szukaniu portfeli wierzchołkowych
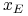 w Wykładzie X.
w Wykładzie X.
-
Etap OUT, gdzie
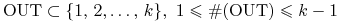 .
.
Szukamy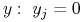 dla
dla 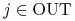 ,
, 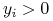 dla
dla
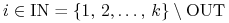 (musi być
co najmniej jedna składowa
(musi być
co najmniej jedna składowa 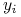 , tj podzbiory IN mają tutaj co najmniej
1 element – różnica w stosunku do podobnego szukania obiektów
, tj podzbiory IN mają tutaj co najmniej
1 element – różnica w stosunku do podobnego szukania obiektów 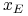 ).
Tzn., zawsze z warunku komplementarności, szukamy wektora dodatnich
rozwiązań układu
).
Tzn., zawsze z warunku komplementarności, szukamy wektora dodatnich
rozwiązań układu 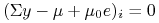 ,
,  takich,
że
takich,
że  dla
dla 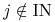 .
.Rozwiązać taki układ da się zawsze, gdyż można go zapisać w zwarty sposób przy pomocy oznaczeń wprowadzonych w Wykładzie X:
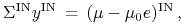
przy czym wyznacznik macierzy
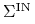 jest jednym z minorów
centralnych macierzy
jest jednym z minorów
centralnych macierzy 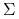 , a więc jest dodatni, bo cały ten algorytm
jest, przypominamy, przy założeniu
, a więc jest dodatni, bo cały ten algorytm
jest, przypominamy, przy założeniu 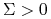 (hasło: twierdzenie Sylvestera
z wykładu GALu, patrz też Wykład II). Także – akcentujemy to jeszcze
raz – dla jednoelementowych zbiorów aktywnych indeksów IN: na głównej
przekątnej macierzy
(hasło: twierdzenie Sylvestera
z wykładu GALu, patrz też Wykład II). Także – akcentujemy to jeszcze
raz – dla jednoelementowych zbiorów aktywnych indeksów IN: na głównej
przekątnej macierzy 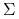 stoją same dodatnie liczby.
stoją same dodatnie liczby.Czytelnik może jednak w tym miejscu zapytać: skoro i tam w Wykładzie X, i teraz tu w opisie nowego algorytmu, używa sie tych samych, zawsze odwracalnych macierzy
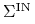 , dlaczego zatem tam pojawiało
się więcej ograniczeń na zbiory IN ?!
, dlaczego zatem tam pojawiało
się więcej ograniczeń na zbiory IN ?!Odpowiedź jest w teorii Blacka i współautorów (Wykład VI), na której, ściana po ścianie, oparty jest poprzedni algorytm. Nie szło w nim tylko o odwracalność macierzy, lecz także o jednoznaczne wyznaczanie współczynników [Lagrange'a]
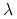 i
i 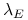 . Dlatego potrzebne są co najmniej dwuelementowe
zbiory IN. I dlatego nie dostaje się tam od razu całej spójnej
łamanej wierzchołkowej
. Dlatego potrzebne są co najmniej dwuelementowe
zbiory IN. I dlatego nie dostaje się tam od razu całej spójnej
łamanej wierzchołkowej 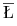 , tylko uboższą
o kilka(naście) wierzchołków Ł – i trzeba osobno pracować
z węzłami wyróżnionymi i ,,ich” portfelami na łamanej.
, tylko uboższą
o kilka(naście) wierzchołków Ł – i trzeba osobno pracować
z węzłami wyróżnionymi i ,,ich” portfelami na łamanej.Wracając do rozwiązania układu
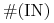 równań w obecnym
algorytmie: otwarta jest sprawa spełniania przez takie rozwiązanie
układu nierówności: ostrych na miejscach o numerach z IN i nieostrych
na miejscach o numerach z OUT. Trzeba to każdorazowo sprawdzać, i
w przypadku niespełniania zwyczajnie przechodzić do następnego
etapu poszukiwań preportfela.
równań w obecnym
algorytmie: otwarta jest sprawa spełniania przez takie rozwiązanie
układu nierówności: ostrych na miejscach o numerach z IN i nieostrych
na miejscach o numerach z OUT. Trzeba to każdorazowo sprawdzać, i
w przypadku niespełniania zwyczajnie przechodzić do następnego
etapu poszukiwań preportfela.Po przebiegnięciu wszystkich
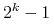 (lub mniej) etapów,
mamy wreszcie preportfel
(lub mniej) etapów,
mamy wreszcie preportfel 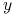 , a wraz z nim portfel optymalny
, a wraz z nim portfel optymalny
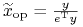 .
.
Przykład 11.3
To właśnie portfela ![]() szuka
się w Zadaniu 3 z kolokwium w dniu 18.XII.2009 – patrz następny
Wykład XII.
szuka
się w Zadaniu 3 z kolokwium w dniu 18.XII.2009 – patrz następny
Wykład XII.
Macierz kowariancji w tamtym zadaniu jest tylko nieujemnie
określona, więc podany tu wyżej algorytm nie stosuje się. Jednak
cała sytuacja jest już na tyle dobrze rozpoznana w trakcie dotychczasowych
wykładów (patrz w szczególności Przykład 7.1), że po wstępnej
analizie od razu wiadomo, na jakim boku trójkąta ![]() należy szukać portfela optymalnego.38i poza tym, generalnie,
na kolokwiach i egzaminach pisemnych z APRK1 można mieć ze sobą
jednostronnie zapisaną kartkę formatu A4 z wzorami, rysunkami,
przykładami, czymkolwiek
należy szukać portfela optymalnego.38i poza tym, generalnie,
na kolokwiach i egzaminach pisemnych z APRK1 można mieć ze sobą
jednostronnie zapisaną kartkę formatu A4 z wzorami, rysunkami,
przykładami, czymkolwiek