13. Wykład XIII, 8.I.2010
Zanim podamy uzasadnienie algorytmicznej40w sytuacjach
niezdegenerowanych metody dochodzenia do portfeli optymalnych
![]() opisanej w Wykładzie XI, pierwszą połowę
tego wykładu chcemy poświęcić alternatywnemu spojrzeniu
na optymalność portfeli w aspekcie M. W tym spojrzeniu
[dominujący w głównym nurcie analizy portfelowej] współczynnik Sharpe'a
zostaje zastąpiony tzw. oczekiwaną użytecznością inwestora.
opisanej w Wykładzie XI, pierwszą połowę
tego wykładu chcemy poświęcić alternatywnemu spojrzeniu
na optymalność portfeli w aspekcie M. W tym spojrzeniu
[dominujący w głównym nurcie analizy portfelowej] współczynnik Sharpe'a
zostaje zastąpiony tzw. oczekiwaną użytecznością inwestora.
Jest to podejście pochodzące od J. von Neumanna i O. Morgensterna –
ich podstawowe dzieło poświęcone tej tematyce to [24]. Podejście
to wykładane jest bardziej systematycznie na kursach mikroekonomii
(także na Wydziale MIM UW; również na WNE, SGH, w Szkole Koźmińskiego,
na LSE …). Dla ogólnego i zgrubnego wyrobienia sobie poglądu na tę
dziedzinę bardzo godny polecenia jest przeglądowy artykuł [15]
dobrze nam znanych autorów Kuhna i Tuckera w zeszycie BAMS
upamiętniającym J. von Neumanna.
Podejście z funkcjami użyteczności prowadzi, przy szukaniu portfeli
– teraz optymalnych w sensie oczekiwanej użyteczności danego
inwestora! – do bardzo naturalnego, kolejnego już w tych wykładach,
użycia twierdzenia K-KT (czyli Twierdzenia 9.2 z Wykładu IX).
Z tego (i z innych) powodu(ów) warto zrobić taki détour.
Gdzie wobec tego w tej chwili jesteśmy? Po Wykładzie XI tkwimy w pewnym
rozkroku, jeśli tak można powiedzieć: jesteśmy w trakcie maksymalizowania
współczynnika Sharpe'a w aspekcie M, lecz wykracza to poza
optymalizację najbardziej przez nas lubianych [różniczkowalnych]
funkcji wklęsłych i wypukłych. Mamy już zasygnalizowane – koniec
Wykładu XI – co należy robić; przy tym przy ![]() – czysto
algorytmicznie.
– czysto
algorytmicznie.
Podczas, gdy ta nowa (dla nas) mgła osiada,41właśnie dlatego
nowy algorytm był podany od razu z marszu w Wykładzie XI – by w
międzyczasie miało co osiadać jest najlepszy moment, by przypomnieć
słowa dawnej oceny twierdzenia K-KT, wypowiedziane przez Góreckiego
i Turowicza w Wiadomościach Matematycznych XII.1 (i przytoczone w
Wykładzie IX w akapicie poprzedzającym Twierdzenie 9.2).
Twierdzenie było zaiste doniosłe. Kuhn i Tucker nadali swojej pracy
[14] taki, a nie inny tytuł celowo. Chcieli oni wyjść poza
rozwiązywanie bardzo wtedy modnych zadań programowania liniowego
(liniowa funkcja celu i liniowe ograniczenia równościowe i nierównościowe)
– i zdołali to zrobić, zaś przed nimi i niezależnie – uczynił to
Karush w [11]. Dlatego nonlinear programming.
Zapowiedziane powyżej zastosowanie twierdzenia K-KT w teorii
użyteczności jest dość świeże w wykładach z APRK1 na Wydziale MIM UW
– datuje się dopiero od roku akademickiego 2007/08.
W podejściu von Neumanna i Morgensterna uważa się (albo: przyjmuje),
że każdy inwestor ma swoją funkcję użyteczności ![]() , którą mierzy
czy ocenia możliwy zysk
, którą mierzy
czy ocenia możliwy zysk ![]() danego scenariusza inwestycyjnego.
Powszechnie przyjmuje się – patrz np już pierwszy rozdział w [1]
– że funkcje użyteczności
danego scenariusza inwestycyjnego.
Powszechnie przyjmuje się – patrz np już pierwszy rozdział w [1]
– że funkcje użyteczności ![]() spełniają trzy aksjomaty (tj, że
inwestorzy tylko po takie funkcje sięgają w swoich podświadomościach,
albo dokładniej: tylko po takie funkcje sięgają ich podświadomości):
spełniają trzy aksjomaty (tj, że
inwestorzy tylko po takie funkcje sięgają w swoich podświadomościach,
albo dokładniej: tylko po takie funkcje sięgają ich podświadomości):
-
A1.
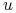 jest rosnąca (inwestor jest nienasycony, ang.
nonsatiation),
jest rosnąca (inwestor jest nienasycony, ang.
nonsatiation), 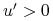 ;
;
-
A2.
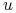 jest wklęsła (inwestor ma awersję do ryzyka,
ang. risk aversion),
jest wklęsła (inwestor ma awersję do ryzyka,
ang. risk aversion), 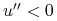 ;
;
-
A3.
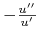 jest malejąca (inwestor ma malejącą
bezwzględną awersję do ryzyka, ang. decreasing absolute
risk awersion).42wielkość
jest malejąca (inwestor ma malejącą
bezwzględną awersję do ryzyka, ang. decreasing absolute
risk awersion).42wielkość 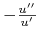 bywa nazywana
miarą Pratta-Arrowa awersji do ryzyka, czyli: w A3 postuluje się
malejącość tej właśnie miary
bywa nazywana
miarą Pratta-Arrowa awersji do ryzyka, czyli: w A3 postuluje się
malejącość tej właśnie miary
Dyskutuje się jeszcze jeden (uzupełniający) aksjomat A4, dotyczący zachowania się względnej awersji do ryzyka inwestora, porównaj [1, strony 24–26], co do zasadności którego nie ma jednak pełnej zgody wśród ekonomistów. Jeden z najbardziej wśród nich znanych, Bawa, ujął to w roku 1975 następująco: ”… decreasing absolute risk aversion is the most restrictive class of utility functions acceptable to most economists.”
Taki ![]() jest zmienną losową z wachlarza (czasem mówi się też:
uniwersum) możliwych scenariuszy inwestycyjnych (biznesowych)
jest zmienną losową z wachlarza (czasem mówi się też:
uniwersum) możliwych scenariuszy inwestycyjnych (biznesowych)
![]() . Zwykle są one wszystkie
określone na tej samej przestrzeni probabilistycznej
. Zwykle są one wszystkie
określone na tej samej przestrzeni probabilistycznej ![]() .
Oczekiwana użyteczność danego scenariusza
.
Oczekiwana użyteczność danego scenariusza ![]() , oznaczana
, oznaczana ![]() ,
to wartość oczekiwana zmiennej losowej
,
to wartość oczekiwana zmiennej losowej ![]() :
:
| (13.1) |
dla ![]() . W teorii użyteczności przyjmuje się,
że inwestor dąży do maksymalizacji oczekiwanej użyteczności
. W teorii użyteczności przyjmuje się,
że inwestor dąży do maksymalizacji oczekiwanej użyteczności
![]() :
:
Jednak na takim poziomie ogólności nie jest to wszystko zbyt … użyteczne. Liczenie oczekiwanych użyteczności zależy przecież od całkowania po trudnych do dokładniejszego sprecyzowania przestrzeniach probabilistycznych. Także problem istnienia scenariusza maksymalizującego oczekiwaną użyteczność jest w ogólności trudny.
Teoria użyteczności sama staje się użyteczna gdy oczekiwana
użyteczność ![]() zależy tylko od kilku dyskretnych parametrów
związanych ze zmienną losową
zależy tylko od kilku dyskretnych parametrów
związanych ze zmienną losową ![]() . Najlepiej – jedynie od wartości
oczekiwanej
. Najlepiej – jedynie od wartości
oczekiwanej ![]() i odchylenia standardowego
i odchylenia standardowego ![]() :
:
| (13.2) |
przy czym, powtórzmy, ![]() cały czas spełnia
(13.1), z funkcją użyteczności
cały czas spełnia
(13.1), z funkcją użyteczności ![]() spełniającą
A1 – A3 +
spełniającą
A1 – A3 +
Przykład 13.1
Wachlarz możliwych scenariuszy inwestycyjnych to zbiór zmiennych
losowych, wyrażających np możliwy zysk z jakiejś dużej planowanej
inwestycji (określonych na tej samej przestrzeni probabilistycznej)
mających rozkłady normalne ![]() , przy podaniu jakichś
rozsądnych przedziałów, z których brane są wartości parametrów
, przy podaniu jakichś
rozsądnych przedziałów, z których brane są wartości parametrów
![]() oraz
oraz ![]() . Natomiast funkcja użyteczności inwestora to
. Natomiast funkcja użyteczności inwestora to
![]() ,
, ![]() , gdzie
, gdzie ![]() jest stałą, która może
podlegać kalibracji (albo: zależy od inwestora).
jest stałą, która może
podlegać kalibracji (albo: zależy od inwestora).
Taka funkcja użyteczności inwestora jest rosnąca (A1) i wklęsła (A2),
choć już bezwzględna awersja do ryzyka takiego inwestora jest stała
(równa ![]() ), nie zaś malejąca – lokujemy się więc na obrzeżach
aksjomatu A3, wystawiając trochę na szwank słowa Bawy.
), nie zaś malejąca – lokujemy się więc na obrzeżach
aksjomatu A3, wystawiając trochę na szwank słowa Bawy.
Jaka jest tutaj oczekiwana użyteczność ![]() ? Po krótkim
i pouczającym rachunku – czytelnik jest zachęcany do wykonania go
samodzielnie – okazuje się być idealna, uzasadniając ex post
cały przykład. Po prostu i nawet bez żadnych przybliżeń (o których
wspomina się niżej, gdy mowa o ogólnym stosowaniu aksjomatów A1 – A3),
? Po krótkim
i pouczającym rachunku – czytelnik jest zachęcany do wykonania go
samodzielnie – okazuje się być idealna, uzasadniając ex post
cały przykład. Po prostu i nawet bez żadnych przybliżeń (o których
wspomina się niżej, gdy mowa o ogólnym stosowaniu aksjomatów A1 – A3),
![]() , jak w (13.2).
, jak w (13.2).
Zatem na poziomicach tej funkcji jedynie od argumentów
![]() i
i ![]() , po rozwikłaniu,
, po rozwikłaniu,
![]() .
Są to funkcje rosnące i wypukłe; nie może być lepiej.
.
Są to funkcje rosnące i wypukłe; nie może być lepiej.
Jak naturalny jest, w teorii użyteczności na styku z analizą portfelową, warunek (13.2), niech świadczy następujący dłuższy cytat z jednej z najważniejszych prac w analizie portfelowej [23]. (Dodajmy, że `individuals' uczestniczący w grze akcjami na giełdzie pojawiają się tam, jak deus ex machina, dopiero w cytowanym twierdzeniu, na dziewiątej stronie pracy.)
Theorem I (a mutual fund theorem). Given m assets satisfying conditions […], there are two portfolios (”mutual funds”) constructed from these m assets, such that all risk-averse individuals, who choose their portfolios so as to maximize utility functions dependent only on the mean and variance of their portfolios, will be indifferent in choosing between portfolios from among the m original assets or these two funds.
To prove Theorem I, it is sufficient to show that any portfolio on the efficient frontier can be attained by a linear combination of two specific portfolios because an optimal portfolio for any individual (as described in the theorem) will be an efficient portfolio.
Podczas kursu APRK2 przedstawiana jest dosyć szeroka klasa rozkładów
zmiennych losowych ![]() , dla których (13.2) ma miejsce.
Teraz musimy się zadowolić tylko stroną praktyczną – zakładać
(13.2) i rozważać konkretne sytuacje związanie z
maksymalizowaniem pewnych funkcji od
, dla których (13.2) ma miejsce.
Teraz musimy się zadowolić tylko stroną praktyczną – zakładać
(13.2) i rozważać konkretne sytuacje związanie z
maksymalizowaniem pewnych funkcji od ![]() ,
gdzie w domyśle
,
gdzie w domyśle ![]() ,
, ![]() dla
dla ![]() .
Przy tym w analizie portfelowej, jak już wspominaliśmy w Wykładzie VII,
wachlarz
.
Przy tym w analizie portfelowej, jak już wspominaliśmy w Wykładzie VII,
wachlarz ![]() to
to ![]() w aspekcie M, względnie
w aspekcie M, względnie ![]() w aspekcie B.
w aspekcie B.
Co więcej można powiedzieć o pojawiających się w taki sposób
funkcjach ![]() ? Dokładniej, co można powiedzieć o
poziomicach takich funkcji, czyli krzywych obojętności
inwestora (ang. indifference curves)?
? Dokładniej, co można powiedzieć o
poziomicach takich funkcji, czyli krzywych obojętności
inwestora (ang. indifference curves)?
Otóż wymienione wcześniej aksjomaty A1 – A3 implikują,43po pewnych
dodatkowych przybliżeniach, w tym: bliskich zaproponowaniu pewnej formy
aksjomatu A4, porównaj też [1] że rozwikłania związków ![]() , tzn. funkcje
, tzn. funkcje ![]() , są rosnące i wypukłe.
, są rosnące i wypukłe.
Właśnie te własności funkcji ![]() są implicite zakładane
w konkretnych zadaniach pojawiających się od pewnego
czasu w kursie APRK1.
są implicite zakładane
w konkretnych zadaniach pojawiających się od pewnego
czasu w kursie APRK1.
Przykład 13.2 (z kolokwium z APRK1 w XII. 2007)
Niech dane (13.6) (na których później jeszcze będzie ćwiczony
i utrwalany algorytm dochodzenia do portfeli optymalnych) definiują taki
model Markowitza, w którym inwestor dodatkowo zna swoją funkcję
oczekiwanej użyteczności ![]() zależną tylko od
zależną tylko od ![]() i
i ![]() danego portfela (czyli scenariusza inwestycyjnego),
danego portfela (czyli scenariusza inwestycyjnego),
| (13.3) |
Należy wyznaczyć portfel optymalny dla tego inwestora,
tj portfel optymalny ze względu na tę funkcję oczekiwanej
użyteczności – po prostu portfel, który ma maksymalną oczekiwaną
użyteczność wśród wszystkich portfeli Markowitza.
Chcemy zatem zmaksymalizować funkcję
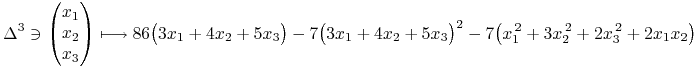 |
(13.4) |
i w pierwszej chwili nie wydaje się to łatwe. Przedstawimy dwa zupełnie różne rozwiązania. Pierwsze opiera się o dodatkową ,,tajemną” wiedzę, która dopiero później znajdzie wyjaśnienie.
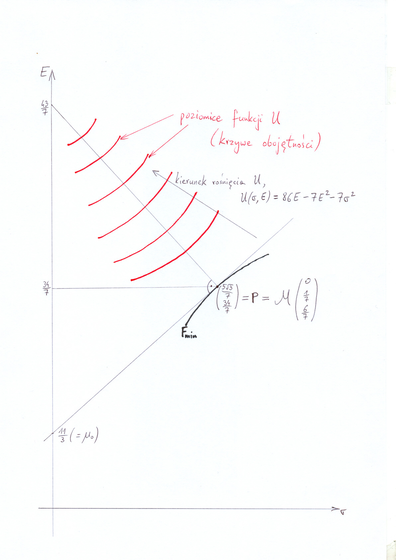
[Rozwiązanie A] Zapisujemy trochę inaczej funkcję
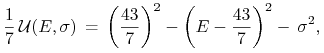 |
przez co widoczne stają się poziomice funkcji
![]() , więc też poziomice
, więc też poziomice ![]() . Są to
części półokręgów (
. Są to
części półokręgów (![]() ) w rodzinie współśrodkowych okręgów
o środku w
) w rodzinie współśrodkowych okręgów
o środku w ![]() , zaznaczone
na czerwono na Rysunku 13.1 poniżej. Okazuje się, że ten wspólny środek
tworzy, z: (a) pewnym punktem
, zaznaczone
na czerwono na Rysunku 13.1 poniżej. Okazuje się, że ten wspólny środek
tworzy, z: (a) pewnym punktem ![]() 44będącym
44będącym ![]() -obrazem
konkretnego portfela efektywnego w aspekcie M – patrz Rysunek 13.1
na granicy minimalnej
-obrazem
konkretnego portfela efektywnego w aspekcie M – patrz Rysunek 13.1
na granicy minimalnej ![]() w tym modelu Markowitza, i z (b) punktem,
w którym prosta styczna w
w tym modelu Markowitza, i z (b) punktem,
w którym prosta styczna w ![]() do
do ![]() przecina oś
przecina oś ![]() ,
trójkąt prostokątny widoczny tu na rysunku.
,
trójkąt prostokątny widoczny tu na rysunku.
[W wersji pdf Rysunek 13.1 przeskakuje aż na następną stronę.]
Upewniamy się o tym bezpośrednim rachunkiem
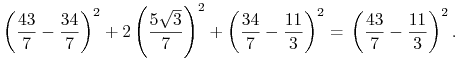 |
Skoro tak, to to już koniec rozwiązania: portfel
![]() ,
który w mapie
,
który w mapie ![]() przechodzi na punkt
przechodzi na punkt ![]() [i który
wypłynie jeszcze w innym zagadnieniu później w tym wykładzie]
okazuje się być optymalny w sensie podanej funkcji oczekiwanej
użyteczności. Wartość
[i który
wypłynie jeszcze w innym zagadnieniu później w tym wykładzie]
okazuje się być optymalny w sensie podanej funkcji oczekiwanej
użyteczności. Wartość
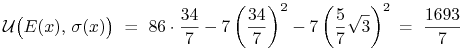 |
jest maksymalna możliwa dla portfeli – scenariuszy inwestycyjnych
z ![]() .
.
W tym rozwiązaniu wsparliśmy się wyciągniętym z kapelusza faktem geometrycznym, który znajdzie swoje objaśnienie dopiero ex post. Czy nie możnaby rozwiązywać takich zadań na ślepo, niejako automatycznie?
Odpowiedź brzmi TAK, ponieważ chodzi tu o maksymalizację funkcji
![]() stojącej po prawej stronie (13.4), która
jest wklęsła i różniczkowalna jako funkcja zmiennych
stojącej po prawej stronie (13.4), która
jest wklęsła i różniczkowalna jako funkcja zmiennych
![]() . Maksymalizacja ma być warunkowa,
przy ograniczeniu równościowym
. Maksymalizacja ma być warunkowa,
przy ograniczeniu równościowym ![]() i ograniczeniach
nierównościowych
i ograniczeniach
nierównościowych ![]() . Mieści się to
dokładnie w zakresie stosowalności twierdzenia K-KT, skąd wyłania się
. Mieści się to
dokładnie w zakresie stosowalności twierdzenia K-KT, skąd wyłania się
[Rozwiązanie B] Szukamy portfela ![]() takiego, że
takiego, że
dla jakiegoś ![]() ; ten drugi warunek to aktualna
postać warunku komplementarności w twierdzeniu K-KT.
; ten drugi warunek to aktualna
postać warunku komplementarności w twierdzeniu K-KT.
Poszukiwanie odbywa się etapami, zaczynając od
Etap 0. ![]() . Warunek
komplementarności oznacza teraz ”
. Warunek
komplementarności oznacza teraz ”![]() ” zamiast ”
” zamiast ”![]() ”,
co łącznie z ograniczeniem równościowym oznacza
”,
co łącznie z ograniczeniem równościowym oznacza
 |
Rozwiązaniem jest
![]() , a więc Etap 0 nie daje
rozwiązania.
, a więc Etap 0 nie daje
rozwiązania.
Etap 1.1. ![]() . Tym razem
warunek komplementarności prowadzi do układu równań
. Tym razem
warunek komplementarności prowadzi do układu równań
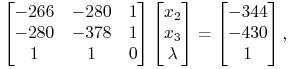 |
i dalej do ![]() .
W tym momencie musimy jeszcze sprawdzić nierówność
.
W tym momencie musimy jeszcze sprawdzić nierówność![]() , tzn. nierówność
, tzn. nierówność ![]() .
Jest ona spełniona (
.
Jest ona spełniona (![]() ), więc procedura opierająca się
o twierdzenie K-KT właśnie znalazła rozwiązanie
), więc procedura opierająca się
o twierdzenie K-KT właśnie znalazła rozwiązanie
![]() ,
to samo, co w Rozwiązaniu A.
,
to samo, co w Rozwiązaniu A.
Twierdzenie K-KT jeszcze raz pokazało swoją siłę.
Zwracamy uwagę, że w tym podejściu funkcja oczekiwanej użyteczności
![]() nie zawsze musi być podana explicite. Znane mogą być
tylko jej poziomice, czyli krzywe obojętności inwestora, bez podania,
jakim wartościom
nie zawsze musi być podana explicite. Znane mogą być
tylko jej poziomice, czyli krzywe obojętności inwestora, bez podania,
jakim wartościom ![]() odpowiadają. Tak było np w zadaniu
z egzaminu z APRK1 ze stycznia 2008.
odpowiadają. Tak było np w zadaniu
z egzaminu z APRK1 ze stycznia 2008.
Ćwiczenie 13.1
Rozpatrujemy model Blacka z ![]() i parametrami
i parametrami ![]() ,
,
![]() ,
, ![]() oraz
oraz ![]() ,
, ![]() .
Wiadomo, że poziomice różniczkowalnej funkcji oczekiwanej użyteczności
inwestora
.
Wiadomo, że poziomice różniczkowalnej funkcji oczekiwanej użyteczności
inwestora ![]() , są łukami współśrodkowych okręgów na płaszczyźnie
, są łukami współśrodkowych okręgów na płaszczyźnie
![]() , mających środek w punkcie
, mających środek w punkcie ![]() , i że
gradient tej funkcji wszędzie patrzy w stronę środka
, i że
gradient tej funkcji wszędzie patrzy w stronę środka ![]() .
.
-
 Znaleźć portfel optymalny w powyższym modelu Blacka ze
względu na taką funkcję oczekiwanej użyteczności
Znaleźć portfel optymalny w powyższym modelu Blacka ze
względu na taką funkcję oczekiwanej użyteczności 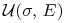 .
Czy ten portfel używa krótkiej sprzedaży?
.
Czy ten portfel używa krótkiej sprzedaży?
-
 Rozważamy rodzinę modeli Blacka o parametrach
Rozważamy rodzinę modeli Blacka o parametrach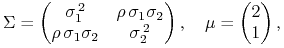
gdzie
 oraz
oraz 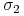 są takie, jak powyżej. Powiększamy
współczynnik korelacji
są takie, jak powyżej. Powiększamy
współczynnik korelacji 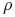 do takiej wartości, że portfel
do takiej wartości, że portfel
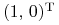 staje się portfelem optymalnym w danym
modelu względem tej samej, niezmienianej funkcji oczekiwanej
użyteczności. Wyznaczyć tę wartość
staje się portfelem optymalnym w danym
modelu względem tej samej, niezmienianej funkcji oczekiwanej
użyteczności. Wyznaczyć tę wartość 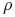 .
.
-
 Wyznaczyć taką (jeszcze większą od poprzedniej)
wartość
Wyznaczyć taką (jeszcze większą od poprzedniej)
wartość 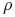 , by portfel
, by portfel 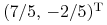 był portfelem
optymalnym w danym modelu Blacka względem tej samej, niezmienianej
funkcji oczekiwanej użyteczności.
był portfelem
optymalnym w danym modelu Blacka względem tej samej, niezmienianej
funkcji oczekiwanej użyteczności.
Pierwsza część zadania
Ze szkoły średniej (ale … przedwojennej) wiadomo, jak wygląda równanie
afinicznej prostej stycznej do hiperboli (3.4) przechodzącej
przez punkt ![]() leżący na tej
hiperboli, konkretnie – obraz portfela szukanego w tej części zadania.
Równanie to ma postać
leżący na tej
hiperboli, konkretnie – obraz portfela szukanego w tej części zadania.
Równanie to ma postać
gdzie podstawiono już znane wartości do [naszego starego] wzoru
(3.3) na ![]() . Znamy więc już wektor prostopadły do
tej prostej stycznej,
. Znamy więc już wektor prostopadły do
tej prostej stycznej,
W warunkach zadania ten wektor powinien być równoległy do wektora
łączącego środek rodziny okręgów ![]() z punktem
z punktem
![]() , tzn. do wektora
, tzn. do wektora
Wobec równych i niezerowych pierwszych składowych obu wektorów, równe muszą też być ich drugie składowe,
skąd ![]() , więc
, więc
![]() .
Widzimy, że ten portfel nie używa krótkiej sprzedaży
(jest portfelem Markowitza).
.
Widzimy, że ten portfel nie używa krótkiej sprzedaży
(jest portfelem Markowitza).
Teraz część druga zadania.
Jeżeli portfel ![]() jest optymalny względem
tej samej funkcji oczekiwanej użyteczności, natomiast inny
jest teraz współczynnik korelacji
jest optymalny względem
tej samej funkcji oczekiwanej użyteczności, natomiast inny
jest teraz współczynnik korelacji ![]() – to właśnie on jest
teraz niewiadomą, zaś wiadome są
– to właśnie on jest
teraz niewiadomą, zaś wiadome są ![]() oraz
oraz ![]() . Równanie prostej stycznej
do pocisku Markowitza w punkcie
. Równanie prostej stycznej
do pocisku Markowitza w punkcie ![]() ma
więc teraz postać
ma
więc teraz postać
gdzie ![]() zgodnie z (3.3).
Stąd jeden z wektorów prostopadłych do tej prostej to
zgodnie z (3.3).
Stąd jeden z wektorów prostopadłych do tej prostej to
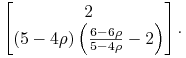 |
W zadaniu postuluje się, by ten wektor był równoległy
do wektora wodzącego idącego od środka okręgów – krzywych
obojętności do punktu styczności ![]() ,
,
co daje równianie
albo ![]() . Współczynnik korelacji zwiększyliśmy
od wyjściowej wartości
. Współczynnik korelacji zwiększyliśmy
od wyjściowej wartości ![]() do
do ![]() i w tym czasie
portfel optymalny w nowym sensie przesunął się do samego krańca
odcinka
i w tym czasie
portfel optymalny w nowym sensie przesunął się do samego krańca
odcinka ![]() .
.
Część trzecia zadania.
Cały czas przedwojenna szkoła średnia: równanie afinicznej prostej
stycznej do hiperboli (3.4) przechodzącej przez punkt ![]() – obraz portfela optymalnego w tej części zadania, ma postać
– obraz portfela optymalnego w tej części zadania, ma postać
(patrz znowu wzór (3.3)). Stąd wektor prostopadły do tej prostej stycznej to
W warunkach zadania ten wektor powinien być równoległy do wektora
łączącego środek rodziny okręgów ![]() z punktem
styczności
z punktem
styczności ![]() ,
tzn. do wektora
,
tzn. do wektora
Skoro ![]() , drugie składowe tych wektorów są równe,
, drugie składowe tych wektorów są równe,
skąd ![]() . Współczynnik korelacji wzrósł dramatycznie
(od wartości
. Współczynnik korelacji wzrósł dramatycznie
(od wartości ![]() ) i w tym czasie portfel optymalny w nowym
sensie przesunął się bardzo znacznie poza odcinek portfeli Markowitza.
) i w tym czasie portfel optymalny w nowym
sensie przesunął się bardzo znacznie poza odcinek portfeli Markowitza.
Jako pewien test, czy ten nowy obszar zastosowań twierdzenia K-KT został już dobrze opanowany, spróbujmy wspólnymi siłami poszukać portfela Markowitza w modelu z parametrami
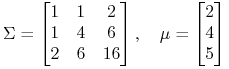 |
optymalnego ze względu na (skądś) znaną funkcję oczekiwanej użyteczności
![]() . No i na koniec policzyć
też, ile ta maksymalna oczekiwana użyteczność wynosi: 50, 75, 100 ?
. No i na koniec policzyć
też, ile ta maksymalna oczekiwana użyteczność wynosi: 50, 75, 100 ?
Mają to być oczekiwane użyteczności portfeli, a więc wprowadzamy funkcję wklęsłą
i różniczkowalną ![]() i pamiętamy o ograniczeniu równościowym
i pamiętamy o ograniczeniu równościowym ![]() oraz o standardowych
ograniczeniach nierównościowych w Markowitzu
oraz o standardowych
ograniczeniach nierównościowych w Markowitzu ![]() ,
, ![]() .
.
Szukamy zatem – właśnie technologia K-KT – takiego(ch) portfela(i) ![]() ,
dla którego(ch) istnieje
,
dla którego(ch) istnieje ![]() taka, że
taka, że ![]() w sensie wektorowym oraz spełniony jest warunek komplementarności
w sensie wektorowym oraz spełniony jest warunek komplementarności
![]() .
.
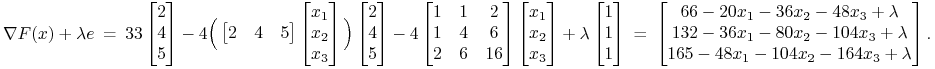 |
(13.5) |
Szukać będziemy etapami.
Etap 0. ![]() . Warunek
komplementarności oznacza teraz wszystkie ”
. Warunek
komplementarności oznacza teraz wszystkie ”![]() ” zamiast ”
” zamiast ”![]() ”, co,
wobec rachunku (13.5) i łącznie z ograniczeniem równościowym
oznacza
”, co,
wobec rachunku (13.5) i łącznie z ograniczeniem równościowym
oznacza
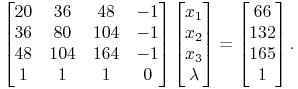 |
Rozwiązaniem jest ![]() ,
a więc Etap 0 na pewno nie da nam rozwiązania.
,
a więc Etap 0 na pewno nie da nam rozwiązania.
Etap 1.1. ![]() . Tym razem, znowu używając
(13.5), warunek komplementarności prowadzi do układu równań
. Tym razem, znowu używając
(13.5), warunek komplementarności prowadzi do układu równań
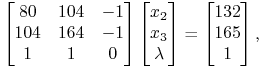 |
i dalej do ![]() .
To już stwarza nadzieję na rozwiązanie, choć musimy jeszcze sprawdzić nierówność
.
To już stwarza nadzieję na rozwiązanie, choć musimy jeszcze sprawdzić nierówność![]() , tzn. nierówność
, tzn. nierówność ![]() .
.
Jest ona spełniona,
![]() ,
więc twierdzenie K-KT właśnie dało nam szukane rozwiązanie
,
więc twierdzenie K-KT właśnie dało nam szukane rozwiązanie
![]() .
.
Liczymy (niemalże) w pamięci, że ![]() oraz
oraz ![]() .
Oczekiwana użyteczność portfela
.
Oczekiwana użyteczność portfela ![]() , maksymalna w aspekcie M, to
, maksymalna w aspekcie M, to
![]() .
.
Wreszcie, jako ostateczny test w zakresie teorii użyteczności, polecamy szczególnie Zadanie 2 w następującym przykładowym zestawie trzech zadań z analizy portfelowej (oferującym też jeszcze pytanie dodatkowe).
Przykład 13.3
We wszystkich dotychczasowych przykładach krzywe obojętności były łukami okręgów, co mogło zachęcać przy szukaniu rozwiązań do alternatywnego sięgania po czystą geometrię analityczną. W zestawie zadań tuż poniżej (Rysunek 13.2, Zadanie 2) krzywe obojętności są łukami elips. Taka okoliczność nie wyklucza stosowania geometrii analitycznej, lecz wyraźnie zwiększa pokusę sięgnięcia po nasze główne narzędzie, czyli twierdzenie K-KT.
[W wersji pdf pierwszy arkusz przeskakuje na następną stronę, zaś drugi – na jeszcze następną.]
(W tym kolokwium trochę inny niż 18.XII.2009 był rozkład punktów za zadania, lecz też do zdobycia było ich łącznie 40, oraz dodatkowo 8 w bonusie za pytanie dodatkowe.)
Przerywamy już tę (za) długo trwającą dygresję o teorii użyteczności; mogła ona trwać jeszcze dłużej, jeśli po drodze rozwiązywało się zadania.
Wracamy do sprawy najważniejszej, czyli do maksymalizowania współczynnika
Sharpe'a w aspekcie M, no i do algorytmu, który ma to robić ,,za nas”.
Dużą część naszej dotychczasowej wiedzy puścimy w ruch w trakcie
dyskusji jednej konkretnej sytuacji. Mianowicie
jednym z dobrze rozpoznanych, jeśli chodzi o łamaną wierzchołkową Ł, jest przykład
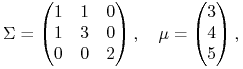 |
(13.6) |
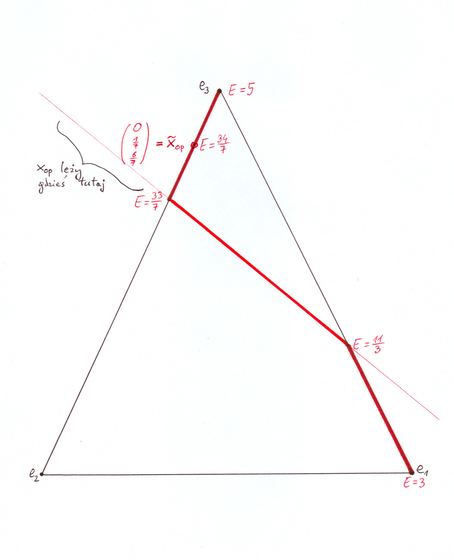
który wystąpił na egzaminie w VI. 2006 i – w innym kontekście – także na kolokwium w XII. 2007, no i także już w tym bieżącym wykładzie (w Przykładzie 13.2, w kontekście teorii użyteczności). Łamana Ł wygląda w nim następująco:
[w wersji pdf Rysunek 13.4 przeskakuje aż dwie strony dalej!]
Zaproponujemy tutaj portfel ![]() , nie
znając jeszcze konkretnej wartości
, nie
znając jeszcze konkretnej wartości ![]() , której on odpowiada.
, której on odpowiada.
![]() poznamy chwilę później, używając już posiadanej wiedzy.
poznamy chwilę później, używając już posiadanej wiedzy.
Niech ![]() będzie środkiem `najwyższego'
boku Ł,
będzie środkiem `najwyższego'
boku Ł, 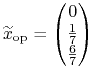 ,
,
![]() .
Ten punkt leży na granicy efektywnej w odpowiednim modelu Markowitza
(granica efektywna w aspekcie M tu zaczyna się dokładnie tam,
gdzie zaczyna się aktywna w modelu Markowitza część pocisku Markowitza).
Styczna do granicy efektywnej w
.
Ten punkt leży na granicy efektywnej w odpowiednim modelu Markowitza
(granica efektywna w aspekcie M tu zaczyna się dokładnie tam,
gdzie zaczyna się aktywna w modelu Markowitza część pocisku Markowitza).
Styczna do granicy efektywnej w ![]() przecina pionową oś
przecina pionową oś ![]() na wysokości
na wysokości ![]() ,
,
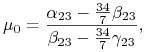 |
gdzie ![]() i
i ![]() są z teorii Blacka
przy
są z teorii Blacka
przy ![]() . Dla tego modelu liczy się je niemalże
w pamięci i wtedy
. Dla tego modelu liczy się je niemalże
w pamięci i wtedy
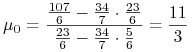 |
(przypadkowo też wysokość przełączenia się granicy minimalnej z
pocisku Markowitza na obraz boku ![]() ). Teraz już
wiemy, że portfel
). Teraz już
wiemy, że portfel ![]() jest optymalny w tym
modelu Markowitza ze względu na stopę bezryzykowną
jest optymalny w tym
modelu Markowitza ze względu na stopę bezryzykowną ![]() .
.
Te słowa rzucają też snop światła na Rysunek 13.1 i dotąd tajemnicze
rozwiązanie A problemu zaproponowanego w Przykładzie 13.2 (tamten
rysunek jest ukryty w rozwiązaniu; trzeba w nie wejść, by go
zobaczyć).
Zobaczmy, jak w tej sytuacji pracuje algorytm podany na Wykładzie XI.
Etap ![]() to [w pierwszej fazie, przed sprawdzaniem ostrych
nierówności], z warunku komplementarności, poszukiwanie portfela
to [w pierwszej fazie, przed sprawdzaniem ostrych
nierówności], z warunku komplementarności, poszukiwanie portfela
![]() optymalnego w Blacku (13.6) ze względu na
tę samą
optymalnego w Blacku (13.6) ze względu na
tę samą ![]() . Otóż ten portfel nie jest Markowitza.
Istotnie, portfel
. Otóż ten portfel nie jest Markowitza.
Istotnie, portfel ![]() na przecięciu boku
na przecięciu boku ![]() i prostej krytycznej Blacka
dla danych (13.6) jest optymalny w takim modelu Blacka ze
względu na
i prostej krytycznej Blacka
dla danych (13.6) jest optymalny w takim modelu Blacka ze
względu na
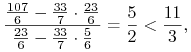 |
a więc ![]() i portfel
i portfel ![]() leży
na prostej krytycznej poza sympleksem
leży
na prostej krytycznej poza sympleksem ![]() .45Jest ćwiczeniem
sprawdzającym znaleźć ten portfel
.45Jest ćwiczeniem
sprawdzającym znaleźć ten portfel ![]() , patrz
też Rysunek 13.4.
, patrz
też Rysunek 13.4.
Etap ![]() to szukanie
to szukanie ![]() ,
,
![]() i
i
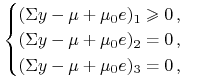 |
co daje ![]() ,
, ![]() , zaś nierówność na
pierwszej składowej
, zaś nierówność na
pierwszej składowej ![]() jest spełniona.
jest spełniona.
Algorytm kończy się więc na tym etapie, dając po normalizacji
![]() zgodnie z oczekiwaniami.
zgodnie z oczekiwaniami.
Nie jest to koniec naszych przykładów szukania portfeli optymalnych w aspekcie M. Takie portfele pojawią się jeszcze w następnym Wykładzie XIV.
Tymczasem jednak niecierpiące zwłoki są zręby ważnej teorii, sięgające wstecz do roku 1965 (praca O. L. Mangasariana [18]) niezbędne do tego, co wymienione w tytule tu poniżej.
Uzasadnienie algorytmicznej metody przedstawionej w Wykładzie XI.
Na samym początku potrzebny jest nam mały rozbieg – musimy cofnąć się do
różniczkowalnych funkcji wypukłych i wklęsłych wielu zmiennych.
Ten temat jest niestety traktowany trochę po macoszemu w kursie AM II
(zresztą tam, jak wiadomo, prawie na nic nie starcza czasu).
Jeśli ![]() ,
,
![]() otwarty wypukły, jest różniczkowalna, wtedy
otwarty wypukły, jest różniczkowalna, wtedy
Także w wersji ostrej, czy ścisłej,
Analogiczna, z nierównościami w przeciwnych kierunkach,
jest charakteryzacja funkcji wklęsłych różniczkowalnych.
(Tej wiedzy zwykle nie uzyskuje się w kursie AM II, lecz dopiero na zajęciach z
Optymalizacji. Tymczasem chodzi tu o zupełnie podstawowe intuicje geometryczne
związane z funkcjami wklęsłymi/wypukłymi wielu zmiennych w ich punktach
różniczkowalności – o podpieranie z góry/dołu wykresów takich funkcji
przez afiniczne przestrzenie styczne do tych wykresów.)
To przypomnienie stanowi motywację i punkt wyjścia do zdefiniowania ogólniejszych własności różniczkowalnych funkcji wielu zmiennych, niż wklęsłość/wypukłość.46na poziomie definicji, sama wklęsłość/wypukłość funkcji nie wymaga różniczkowalności
Definicja 13.1 ([18])
-
 Powiemy, że
Powiemy, że 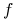 j. w. jest pseudo-wklęsła gdy
j. w. jest pseudo-wklęsła gdy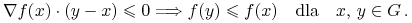
-

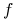 j. w. jest pseudo-wypukła gdy
j. w. jest pseudo-wypukła gdy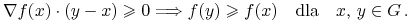
Obserwacja. 13.1 Funkcja różniczkowalna wklęsła (wypukła) jest także pseudo-wklęsła (pseudo-wypukła).
Wynika to od razu z Definicji 13.1, po wykorzystaniu przypomnianych chwilę wcześniej charakteryzacji funkcji wklęsłych i wypukłych różniczkowalnych.
Uwaga 13.1
Na odwrót nie, bo np funkcja ![]() nie jest ani wklęsła, ani wypukła, natomiast jest ona zarówno
pseudo-wklęsła, jak i pseudo-wypukła.
nie jest ani wklęsła, ani wypukła, natomiast jest ona zarówno
pseudo-wklęsła, jak i pseudo-wypukła.
Istotnie, ![]() , natomiast
, natomiast
![]() i pierwsze
czynniki w tych wyrażeniach iloczynowych są zawsze dodatnie.
i pierwsze
czynniki w tych wyrażeniach iloczynowych są zawsze dodatnie.