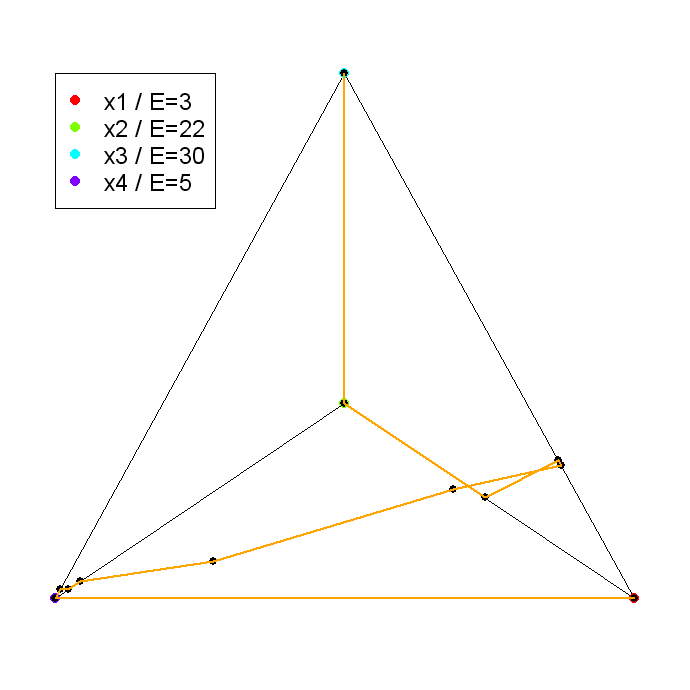15. Wykład XV, 22.I.2010
Przystępujemy do opisu działania CLA; komentarze objaśniające będą podane później, by nie zaciemniać głównej, pięknej pętli algorytmu.
Zakładamy już do końca, że ![]() oraz
oraz
![]() . To pociąga, że
macierze
. To pociąga, że
macierze ![]() , a także
, a także ![]() , są odwracalne
dla wszystkich
, są odwracalne
dla wszystkich ![]() – patrz Twierdzenie w Wykładzie XIV.
Algorytm CLA odnajduje, na nowo i niezależnie od metody prób opartej
na twierdzeniu Karusha-Kuhna-Tuckera (patrz Wykład X), łamaną wierzchołkową
– patrz Twierdzenie w Wykładzie XIV.
Algorytm CLA odnajduje, na nowo i niezależnie od metody prób opartej
na twierdzeniu Karusha-Kuhna-Tuckera (patrz Wykład X), łamaną wierzchołkową
![]() zbudowaną z portfeli relatywnie minimalnego ryzyka.
Względnie– w oryginalnej prezentacji Markowitza w [22] –
tylko łamaną efektywną, co jest różnicą mało istotną z punktu widzenia
metodologii CLA. Najczęściej sprawnie i bezbłędnie odnajduje on tych
,,kilkaset boków”
zbudowaną z portfeli relatywnie minimalnego ryzyka.
Względnie– w oryginalnej prezentacji Markowitza w [22] –
tylko łamaną efektywną, co jest różnicą mało istotną z punktu widzenia
metodologii CLA. Najczęściej sprawnie i bezbłędnie odnajduje on tych
,,kilkaset boków” ![]() , jak wyraża się Markowitz,
spośród setek tysięcy czy milionów ścian sympleksu, przez które à
priori mogłaby przebiegać
, jak wyraża się Markowitz,
spośród setek tysięcy czy milionów ścian sympleksu, przez które à
priori mogłaby przebiegać ![]() . Redukuje problem o
potencjalnej złożoności wykładniczej od
. Redukuje problem o
potencjalnej złożoności wykładniczej od ![]() do problemu w praktyce
wielomianowego od
do problemu w praktyce
wielomianowego od ![]() , i to wielomianowego – wydaje się, jest to
otwarte pole do badań – bardzo niskiego stopnia.
, i to wielomianowego – wydaje się, jest to
otwarte pole do badań – bardzo niskiego stopnia.
Skoncentrujmy uwagę na jednej ustalonej ścianie IN,
w której leży jeden z boków ![]() .
W tym obecnym spojrzeniu może to nawet być jeden z wierzchołków
sympleksu
.
W tym obecnym spojrzeniu może to nawet być jeden z wierzchołków
sympleksu ![]() , oczywiście taki, przez który przechodzi
, oczywiście taki, przez który przechodzi
![]() . Tzn.
. Tzn. ![]() jest możliwe.
jest możliwe.
Zakładamy, że algorytm już doszedł do boku ![]() leżącego w IN i biegnie po nim (lub stoi, gdy
leżącego w IN i biegnie po nim (lub stoi, gdy ![]() ,
zmniejszając przy tym wartość parametru
,
zmniejszając przy tym wartość parametru ![]() .
.
Jak długo to się dzieje, tzn. jak długo utrzymuje się relatywna
optymalność portfeli – punktów na tym boku? Oczywiście, z
twierdzenia K-KT, dopóki
oraz
Dodatniość, względnie nieujemność, może przy zmniejszaniu
![]() popsuć się tylko w tych wyrażeniach, w których
współczynniki przy
popsuć się tylko w tych wyrażeniach, w których
współczynniki przy ![]() są dodatnie.
Wynikają stąd naturalne dolne ograniczenia
są dodatnie.
Wynikają stąd naturalne dolne ograniczenia
oraz
Kresem dolnym optymalności portfeli na ścianie IN, wyrażonym
w terminach parametru ![]() , jest zatem
, jest zatem
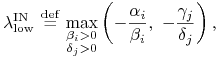 |
(15.1) |
gdzie też oczywiście ![]() ,
, ![]() . Gdy
. Gdy
![]() ,
, ![]() , wtedy nie ma aktywnej
nierówności na temat
, wtedy nie ma aktywnej
nierówności na temat ![]() , są tylko pewne nierówności na temat
, są tylko pewne nierówności na temat
![]() ,
, ![]() , związane z optymalnością wierzchołka numer
, związane z optymalnością wierzchołka numer
![]() oraz związanymi z tym możliwymi wartościami parametru
oraz związanymi z tym możliwymi wartościami parametru
![]() .56wtedy, jak wiadomo, rozwiązania warunków
Karusha-Kuhna-Tuckera nie dają jednoznacznie wyznaczonych
współczynników Lagrange'a
.56wtedy, jak wiadomo, rozwiązania warunków
Karusha-Kuhna-Tuckera nie dają jednoznacznie wyznaczonych
współczynników Lagrange'a ![]() i
i ![]()
Algorytm będzie ,,wiedział”, gdzie skierować się dalej (gdzie
leży następny bok łamanej ![]() ) gdy zawsze tylko
jedna liczba z tych wymienionych po prawej stronie równości (15.1)
realizuje dane maksimum. W celu zapewnienia skuteczności algorytmu CLA
będziemy to zakładali do końca wykładu. Dokładniej,
) gdy zawsze tylko
jedna liczba z tych wymienionych po prawej stronie równości (15.1)
realizuje dane maksimum. W celu zapewnienia skuteczności algorytmu CLA
będziemy to zakładali do końca wykładu. Dokładniej,
Definicja 15.1
O modelu Markowitza ![]() ,
, ![]() ,
,
![]() , mówimy, że ma
, mówimy, że ma
niezdegenerowane parametry gdy
| (15.2) |
Komentarz po definicji: zakładając w dalszym ciągu
niezdegenerowanie parametrów modelu, zakładamy w tym wykładzie więcej,
niż jest potrzebne do sprawnego przebiegu algorytmu (choć i tak mniej,
niż u Markowitza w [22]). Bo przecież nie wszystkie ściany IN
muszą być odwiedzone przez konkretną łamaną ![]() oraz,
dla jakiegokolwiek danego IN, który występuje w konkretnym
przebiegu algorytmu, nie wszystkie ułamki wymienione w (15.2)
muszą być różne! Tylko największy z nich musi być różny
od wszystkich pozostałych.
oraz,
dla jakiegokolwiek danego IN, który występuje w konkretnym
przebiegu algorytmu, nie wszystkie ułamki wymienione w (15.2)
muszą być różne! Tylko największy z nich musi być różny
od wszystkich pozostałych.
Uwaga 15.1
Gdy patrzymy na formułę (15.1), czy też na dualną formułę (15.22),
która pojawi się [dopiero] pod koniec tego wykładu, nie sposób nie zauważyć
ich dużego podobieństwa z formułami, jakie występują w programowaniu
liniowym. Można przykładowo spojrzeć na wzory na stronie 126 w klasycznej
książce [7] poświęconej programowaniu liniowemu, czy też na
towarzyszącą im dyskusję na stronach sąsiednich tamże.
W istocie to, czym od strony technicznej zajmuje się analiza portfelowa,
to programowanie kwadratowe, oczywiście ze specyficznymi
ograniczeniami ,,portfelowymi”. Ekstremalizacja funkcji wypukłej
bądź wklęsłej (bądź też, jak w Wykładzie XIV, pseudo-wklęsłej),
a więc zasadniczo twierdzenie K-KT, nierówności opisujące wypukłą
dziedzinę takiej funkcji i równocześnie pochodne nierówności typu K-KT
wiążące się z ekstremalizacją tej funkcji – stąd biorą się dwie
rodziny ułamków, w których teraz łącznie szukamy liczby najmniejszej
bądź największej. O tyle57słynna Passentowska mała różnica,
którą chciałoby się umieć zagrać – na jakim instrumencie? programowanie
kwadratowe jest bogatsze od liniowego. Przypominamy jeszcze raz tytuł
przełomowej pracy [14]: nonlinear programming.
Warto też jeszcze rzucić okiem na sam tytuł książki [17],
albo też przewertować ją dokładniej.
W książce Gassa jedna rodzina ułamków jest poddawana ekstremalizacji
w każdym kroku algorytmu sympleks, zaś teraz są temu
poddawane równocześnie dwie rodziny różnego pochodzenia.
Opis algorytmu CLA dla modeli z niezdegenerowanymi parametrami
A. Zaczynamy od ![]() , gdzie
, gdzie ![]() , tzn. od
wierzchołka
, tzn. od
wierzchołka ![]() , w którym zaczyna się łamana wierzchołkowa
, w którym zaczyna się łamana wierzchołkowa
![]() . Algorytm przez długi czas stoi na tym wierzchołku,
podczas gdy parametr
. Algorytm przez długi czas stoi na tym wierzchołku,
podczas gdy parametr ![]() maleje od
maleje od ![]() do wartości
do wartości
![]() .
Ta wartość progowa, na mocy niezdegenerowania parametrów modelu, jest
równa
.
Ta wartość progowa, na mocy niezdegenerowania parametrów modelu, jest
równa ![]() dla jednego jedynego
dla jednego jedynego ![]() ,
,
![]() . Stąd wiemy, że następnym etapem będzie
. Stąd wiemy, że następnym etapem będzie
![]() , w którym
parametr
, w którym
parametr ![]() będzie się zmniejszał poniżej wartości
będzie się zmniejszał poniżej wartości
![]() .
.
B. Załóżmy, że już trwa jakiś etap IN w algorytmie, zaś ![]() zmniejsza się poniżej poznanej już poprzedniej wartości progowej.
Afiniczne od
zmniejsza się poniżej poznanej już poprzedniej wartości progowej.
Afiniczne od ![]() wzory na
wzory na ![]() ,
, ![]() , opisują
bok
, opisują
bok ![]() na ścianie IN, dla
na ścianie IN, dla ![]() poniżej poprzedniej
wartości progowej aż do wartości
poniżej poprzedniej
wartości progowej aż do wartości ![]() danej wzorem (15.1).
Na mocy niezdegenerowania parametrów modelu, w (15.1)
jest jeden jedyny indeks
danej wzorem (15.1).
Na mocy niezdegenerowania parametrów modelu, w (15.1)
jest jeden jedyny indeks ![]() lub
lub ![]() taki, że
taki, że ![]() lub
lub ![]() .
.
Następny etap algorytmu to ![]() w pierwszym przypadku, względnie
w pierwszym przypadku, względnie ![]() w
drugim, przy czym parametr
w
drugim, przy czym parametr ![]() zmniejsza się w nim poniżej
zmniejsza się w nim poniżej
![]() (do jakiejś wartości lub do
(do jakiejś wartości lub do ![]() ).
W ten sposób rekurencyjnie podany jest już cały algorytm,
opisujący bok po boku całą łamaną wierzchołkową
).
W ten sposób rekurencyjnie podany jest już cały algorytm,
opisujący bok po boku całą łamaną wierzchołkową ![]() .
Ostatni etap to, oczywiście,
.
Ostatni etap to, oczywiście, ![]() ,
,
![]() ,
zaś
,
zaś ![]() zmniejsza się w nim od poprzedniej wartości progowej
do
zmniejsza się w nim od poprzedniej wartości progowej
do ![]() (przyjmujemy, że maksimum pustego zbioru liczb wynosi
(przyjmujemy, że maksimum pustego zbioru liczb wynosi
![]() ).
).
Komentarz po opisie algorytmu. Stosując algorytm CLA,
rekurencyjnie wędrujemy po niektórych ścianach sympleksu ![]() ,
włączając w to niektóre wierzchołki, cały czas ściśle kontrolując
malejącą ewolucję wiodącego parametru
,
włączając w to niektóre wierzchołki, cały czas ściśle kontrolując
malejącą ewolucję wiodącego parametru ![]() . Po drodze
uzyskujemy parametryczne opisy boków łamanej wierzchołkowej
. Po drodze
uzyskujemy parametryczne opisy boków łamanej wierzchołkowej
![]() wraz z progowymi wartościami parametru
wraz z progowymi wartościami parametru ![]() odpowiadającymi wierzchołkom spójnej łamanej
odpowiadającymi wierzchołkom spójnej łamanej ![]() .
.
Algorytm jest wydajny w ![]() – wędrujemy w nim dokładnie po tych
ścianach
– wędrujemy w nim dokładnie po tych
ścianach ![]() , przez które przebiega łamana
, przez które przebiega łamana ![]() .
Czasami zdarza się – o czym Markowitz w [22] wydaje się
nie wiedzieć – że ten maksymalnie wydajny algorytm musi odwiedzić
wszystkie
.
Czasami zdarza się – o czym Markowitz w [22] wydaje się
nie wiedzieć – że ten maksymalnie wydajny algorytm musi odwiedzić
wszystkie ![]() niepuste ściany
niepuste ściany ![]() .
Tak właśnie dzieje się w przykładzie Więcha omówionym w Wykładzie X,
i też w przykładzie Iwanickiego w wymiarze 5 omawianym tutaj poniżej
(czy też w, tylko wzmiankowanym pod koniec Wykładu VII, nie–praw–do–po–dob–nym
przykładzie Iwanickiego w wymiarze 6).
.
Tak właśnie dzieje się w przykładzie Więcha omówionym w Wykładzie X,
i też w przykładzie Iwanickiego w wymiarze 5 omawianym tutaj poniżej
(czy też w, tylko wzmiankowanym pod koniec Wykładu VII, nie–praw–do–po–dob–nym
przykładzie Iwanickiego w wymiarze 6).
Przykład 15.1 (Więch [29], kontynuacja)
Odnajdywanie łamanej ![]() zaczynamy
od
zaczynamy
od ![]() , bo
, bo ![]() .
.
![]() ,
wchodzi indeks 2,
,
wchodzi indeks 2, ![]() . Kolejne
. Kolejne
![]() ,
wychodzi indeks
,
wychodzi indeks ![]() ,
, ![]() . Kolejne
. Kolejne
![]() , wchodzi indeks
, wchodzi indeks
![]() , itd. Z tabeli w Wykładzie X odczytujemy, jadąc od dołu
do góry, kolejne etapy. Po
, itd. Z tabeli w Wykładzie X odczytujemy, jadąc od dołu
do góry, kolejne etapy. Po ![]() etap
etap ![]() ,
następnie
,
następnie ![]() .
.
Odpowiednie wartości progowe ![]() są w
środkowej kolumnie tamtej tabeli, też jadąc od dołu do góry:
są w
środkowej kolumnie tamtej tabeli, też jadąc od dołu do góry:
![]() , itd.
Istotnie zatem, łamana
, itd.
Istotnie zatem, łamana ![]() w przykładzie
Więcha odwiedza wszystkie podzbiory zbioru
w przykładzie
Więcha odwiedza wszystkie podzbiory zbioru ![]() poza pustym. Ten przykład w chwili pojawienia się jesienią 2001
stanowił prawdziwą sensację.
poza pustym. Ten przykład w chwili pojawienia się jesienią 2001
stanowił prawdziwą sensację.
A oto jak łamana wierzchołkowa w przykładzie Więcha wygląda w rzucie na płaszczyznę ekranu bądź rysunku, przy odpowiednim wyborze kierunku rzutowania:
[w wersji pdf Rysunek 15.1 jest na następnej stronie]
Jeszcze bardziej intrygujący przykład podał w roku 2007 w swojej pracy licencjackiej [9] student A. Iwanicki; anonsowaliśmy to odkrycie już w Wykładzie VII.58Iwanicki wyszedł od programu dla Critical Line Algorithm (w Visual Basicu) autorstwa G. P. Todda, podanego w [22], lecz udoskonalił go przez wprowadzenie pomysłowych shortcutów i dodanie własnej części probabilistycznej – losowanie próbek danych. Jego program wykonywał przez jedną noc najpierw dziesiątki, a potem nawet setki tysięcy przebiegów algorytmu CLA na próbnych danych! Przykład podany w tekście wykładu został znaleziony po około 8 dobach poszukiwań netto. Bez algorytmu CLA, i bez książki [22] jako wstępnego inputu, nie byłoby to możliwe. Jest to najbogatszy możliwy przykład w wymiarze 5. Ma on granicę minimalną składającą się z 26 kawałków różnych hiperbol, zaś granica efektywna składa się w nim z (aż) 19 kawałków różnych hiperbol!
 |
Zgodnie z tym, co wyżej zaanonsowane, łamana wierzchołkowa
okazuje się mieć tu aż ![]() boków, natomiast
algorytm CLA odnajduje ją w
boków, natomiast
algorytm CLA odnajduje ją w ![]() krokach IN,
krokach IN,
![]() . Kolejne kroki są następujące.
(Przy wierzchołkach dających punkty załamania granicy minimalnej
podajemy w nawiasach przedziały dla ,,nadstycznego” parametru
. Kolejne kroki są następujące.
(Przy wierzchołkach dających punkty załamania granicy minimalnej
podajemy w nawiasach przedziały dla ,,nadstycznego” parametru ![]() ;
dyskusja nt tych przedziałów – patrz Stwierdzenie 15.1
niżej. Wielkości
;
dyskusja nt tych przedziałów – patrz Stwierdzenie 15.1
niżej. Wielkości ![]() są tożsame z wielkościami
są tożsame z wielkościami
![]() w etapach bezpośrednio poprzedzających,
porównaj Obserwacja 15.1, część
w etapach bezpośrednio poprzedzających,
porównaj Obserwacja 15.1, część ![]() , poniżej.)
, poniżej.)
Ćwiczenie 15.1
Policzyć do końca tę łamaną wierzchołkową, a następnie zobrazować
ją na rzucie sympleksu ![]() na płaszczyznę (możliwym, tak
jak możliwy jest rzut hipersześcianu na płaszczyznę, itd.).
na płaszczyznę (możliwym, tak
jak możliwy jest rzut hipersześcianu na płaszczyznę, itd.).
Uzasadnienie poprawności algorytmu CLA wraz z dodatkowymi informacjami na jego temat.
Chcemy dokładniej przyjrzeć się, co się dzieje, gdy łamana
wierzchołkowa ![]() , odkrywana stopniowo
przez algorytm CLA, zmienia
, odkrywana stopniowo
przez algorytm CLA, zmienia
(A) ścianę IN, ![]() , na inną ścianę
, na inną ścianę
![]() , względnie
, względnie
(B) ścianę IN, ![]() na wierzchołek,
np
na wierzchołek,
np ![]() , po którym z kolei łamana
, po którym z kolei łamana ![]() wchodzi w ścianę
wchodzi w ścianę ![]() .
.
Uwaga 15.2
Sytuacje (A) i (B) można też scharakteryzować/rozróżnić inaczej.
Mianowicie, pamiętamy jeszcze z dowodu Twierdzenia 10.1,
że parami rozłączne przedziały ![]() ,
, ![]() ,
dają w sumie z węzłami wyróżnionymi cały przedział
,
dają w sumie z węzłami wyróżnionymi cały przedział ![]() .
W sytuacji (A) domknięcia przedziałów
.
W sytuacji (A) domknięcia przedziałów ![]() oraz
oraz ![]() zahaczają się zatem jednym punktem
zahaczają się zatem jednym punktem ![]() .
Jest to jeden z węzłów w Twierdzeniu 10.1, przy czym węzeł
niewyróżniony: łamana przechodząc ze ściany IN na ścianę
.
Jest to jeden z węzłów w Twierdzeniu 10.1, przy czym węzeł
niewyróżniony: łamana przechodząc ze ściany IN na ścianę
![]() nie przechodzi przez żaden wierzchołek sympleksu.
Ten wspólny kres leży więc w dokładnie jednym z przedziałów
nie przechodzi przez żaden wierzchołek sympleksu.
Ten wspólny kres leży więc w dokładnie jednym z przedziałów
![]() ,
, ![]() .
.
Natomiast sytuacja (B) to po prostu inne wypowiedzenie
zdania `![]() jest węzłem wyróżnionym' – porównaj
definicję węzłów wyróżnionych w dowodzie Twierdzenia 10.1
na początku Wykładu XI.
jest węzłem wyróżnionym' – porównaj
definicję węzłów wyróżnionych w dowodzie Twierdzenia 10.1
na początku Wykładu XI.
Tak więc, w telegraficznym skrócie, sytuacja (A) – węzły niewyróżnione, sytuacja (B) – węzły wyróżnione.
W naszych rozważaniach pomocna będzie funkcja wypukła
| (15.3) |
której dotyczył już Wniosek 11.1 w Wykładzie XI.
Jako funkcja wypukła, ma ona wszędzie skończone pochodne jednostronne,
zaś w punktach różniczkowalności ma pochodną o wartości ![]() ,
gdzie
,
gdzie ![]() to funkcja związana z danym bokiem łamanej Ł
leżącym na jakiejś ścianie
to funkcja związana z danym bokiem łamanej Ł
leżącym na jakiejś ścianie ![]() -wymiarowej. (Przy rygorystycznym
podejściu ta funkcja powinna być oznaczana symbolem
-wymiarowej. (Przy rygorystycznym
podejściu ta funkcja powinna być oznaczana symbolem ![]() .
Na ścianach IN,
.
Na ścianach IN, ![]() , współczynniki Lagrange'a
, współczynniki Lagrange'a
![]() i
i ![]() są wyznaczone jednoznacznie jako funkcje
portfela wierzchołkowego, a więc też jako funkcje
są wyznaczone jednoznacznie jako funkcje
portfela wierzchołkowego, a więc też jako funkcje ![]() .) Wynika
to wprost z Obserwacji 6.1 w Wykładzie VI; wspominaliśmy nie raz,
że tamta obserwacja jest technicznie bardzo użyteczna.
.) Wynika
to wprost z Obserwacji 6.1 w Wykładzie VI; wspominaliśmy nie raz,
że tamta obserwacja jest technicznie bardzo użyteczna.
W związku z tym globalna funkcja ![]() ,
,
jest ściśle rosnąca i kawałkami liniowa, z możliwymi skokami w górę:
— w węzłach wyróżnionych, jak np w przykładzie Więcha na rysunku powyżej,
— co widzieliśmy przy okazji rozwiązywania zadania sprawdzającego z Wykładu X,
— oraz być może w jakichś węzłach niewyróżnionych – tego jeszcze w tym momencie nie wiemy; w przykładzie Więcha – bez takich skoków w węzłach niewyróżnionych.
Odcinki, na których funkcja ![]() jest liniowa, etykietujemy odpowiednimi zbiorami indeksów IN –
nazwami ścian, których dotyczą. Węzły wyróżnione, w których jest
skok funkcji
jest liniowa, etykietujemy odpowiednimi zbiorami indeksów IN –
nazwami ścian, których dotyczą. Węzły wyróżnione, w których jest
skok funkcji ![]() , nazywamy pojedynczymi indeksami –
numerami odpowiednich wierzchołków sympleksu. Przejście od
parametru
, nazywamy pojedynczymi indeksami –
numerami odpowiednich wierzchołków sympleksu. Przejście od
parametru ![]() do
do ![]() jest w takich węzłach rodzajem
blow-upu: rozdmuchania punktu do odcinka [wartości parametru
jest w takich węzłach rodzajem
blow-upu: rozdmuchania punktu do odcinka [wartości parametru ![]() ].
].
Niech dla IN : ![]() ,
, ![]() będzie jak
w dowodzie w Wykładzie XI (zbiór wartości oczekiwanych wszystkich
portfeli wierzchołkowych
będzie jak
w dowodzie w Wykładzie XI (zbiór wartości oczekiwanych wszystkich
portfeli wierzchołkowych ![]() leżących na ścianie IN).
leżących na ścianie IN).
Niech ponadto, tym razem dla wszystkich IN niepustych,
![]() oznacza zbiór wszystkich wartości
współczynników Lagrange'a
oznacza zbiór wszystkich wartości
współczynników Lagrange'a ![]() w rozwiązaniach warunków
K-kT dla portfeli wierzchołkowych leżących na ścianie IN.
w rozwiązaniach warunków
K-kT dla portfeli wierzchołkowych leżących na ścianie IN.
Gdy ![]() , jest to (wiemy to już!)
przedział – obraz odpowiedniego przedziału
, jest to (wiemy to już!)
przedział – obraz odpowiedniego przedziału ![]() w globalnej funkcji
w globalnej funkcji ![]() :
:
Natomiast gdy ![]() ,
,
| (15.4) |
bo dla ![]() i
i
![]() ,
, ![]() , nierówności wektorowe
, nierówności wektorowe
pociągają (też wektorową) nierówność
zaś warunki komplementarności
oczywiście pociągają warunek
Istotnie zatem ![]() .
.
Uwaga 15.3
W języku używanym w tym Wykładzie XV, całkiem naturalnym
dla algorytmu CLA, wierzchołek ![]() sympleksu
sympleksu ![]() występuje po prostu jako singleton
występuje po prostu jako singleton ![]() – pewien
jednoelementowy podzbiór zbioru numerów wszystkich
wierzchołków sympleksu. Jest to na tyle naturalne,
że nie powinno powodować nieporozumień.59Symbolika
– pewien
jednoelementowy podzbiór zbioru numerów wszystkich
wierzchołków sympleksu. Jest to na tyle naturalne,
że nie powinno powodować nieporozumień.59Symbolika
![]() pozostaje w użyciu gdy opuszczamy język CLA, np tu
powyżej w samym uzasadnieniu faktu (15.4), lub gdy
dyskutujemy zachowanie konkretnych odwzorowań Markowitza
w punktach ekstremalnych sympleksu.
pozostaje w użyciu gdy opuszczamy język CLA, np tu
powyżej w samym uzasadnieniu faktu (15.4), lub gdy
dyskutujemy zachowanie konkretnych odwzorowań Markowitza
w punktach ekstremalnych sympleksu.
![]() jest zatem przedziałem, ok, lecz jakim konkretnie?
To pytanie jest technicznie najtrudniejsze w całej dyskusji
algorytmu CLA. Zajmiemy się nim za chwilę przy omawianiu
sytuacji (B).
jest zatem przedziałem, ok, lecz jakim konkretnie?
To pytanie jest technicznie najtrudniejsze w całej dyskusji
algorytmu CLA. Zajmiemy się nim za chwilę przy omawianiu
sytuacji (B).
Wracamy teraz do alternatywy (A) versus (B) sformułowanej na
początku dyskusji poprawności algorytmu CLA. (Rzecz dotyczy węzłów
leżących w przedziale ![]() . Po Uwadze 15.2
wiemy już, że to jest po prostu alternatywa węzły niewyróżnione
versus wyróżnione.)
. Po Uwadze 15.2
wiemy już, że to jest po prostu alternatywa węzły niewyróżnione
versus wyróżnione.)
Ad (A) Wobec ścisłej wypukłości funkcji
(15.3) i geometrycznej interpretacji współczynnika
![]() , przedziały
, przedziały ![]() oraz
oraz ![]() są
rozłączne. Chcemy uzasadnić, że ich domknięcia przecinają się w
jednym punkcie, który zresztą okaże się leżeć w jednym z tych
przedziałów:
są
rozłączne. Chcemy uzasadnić, że ich domknięcia przecinają się w
jednym punkcie, który zresztą okaże się leżeć w jednym z tych
przedziałów: ![]() lub
lub ![]() .
.
Punkt ![]() leżący w części wspólnej domknięć
leżący w części wspólnej domknięć
![]() i
i ![]() jest w
sytuacji (A) węzłem niewyróżnionym – wiemy to z dowodu (podanego
w Wykładzie XI) Twierdzenia 10.1 o łamanej wierzchołkowej
z Wykładu X.
jest w
sytuacji (A) węzłem niewyróżnionym – wiemy to z dowodu (podanego
w Wykładzie XI) Twierdzenia 10.1 o łamanej wierzchołkowej
z Wykładu X.
Pokażemy, że w węźle niewyróżnionym ![]() globalna funkcja
globalna funkcja
![]() nie ma skoku. Dla ustalenia uwagi niech
np
nie ma skoku. Dla ustalenia uwagi niech
np ![]() ,
, ![]() . Dla wartości
. Dla wartości ![]() trochę mniejszych od
trochę mniejszych od
![]() bierzemy, jednoznacznie określone w
etapie
bierzemy, jednoznacznie określone w
etapie ![]() dowodu z Wykładu XI, wielkości
dowodu z Wykładu XI, wielkości
oraz ich granice
tak jak w tamtym dowodzie w Wykładzie XI. Z warunków dawanych przez twierdzenie K-KT mamy
dla ![]() trochę mniejszych od
trochę mniejszych od ![]() . Zatem również
po przejściu granicznym
. Zatem również
po przejściu granicznym ![]() ,
,
Portfel ![]() leży na ścianie IN, zaś współczynniki
Lagrange'a dla portfeli wierzchołkowych leżących na ścianie IN
są wyznaczone jednoznacznie. A więc, w szczególności,
leży na ścianie IN, zaś współczynniki
Lagrange'a dla portfeli wierzchołkowych leżących na ścianie IN
są wyznaczone jednoznacznie. A więc, w szczególności,
![]() liczone
na boku leżącym na ścianie IN. Zatem to właśnie liczba
liczone
na boku leżącym na ścianie IN. Zatem to właśnie liczba
![]() okazuje się leżeć w części wspólnej
domknięć przedziałów
okazuje się leżeć w części wspólnej
domknięć przedziałów ![]() i
i ![]() .
Dokładniej,
.
Dokładniej,
| (15.5) |
przy czym ![]() .
Równocześnie
.
Równocześnie
| (15.6) |
oraz ![]() , bo,
przypominamy,
, bo,
przypominamy, ![]() i
i ![]() są rozłączne.
są rozłączne.
W sytuacji przeciwnej w (A): ![]() ,
lecz
,
lecz ![]() byłoby, oczywiście,
byłoby, oczywiście,
![]() oraz
oraz
![]() ,
natomiast równości (15.5)–(15.6) oczywiście
pozostawałyby w mocy.
,
natomiast równości (15.5)–(15.6) oczywiście
pozostawałyby w mocy.
Wniosek 15.1
Obraz [w odwzorowaniu Markowitza] każdego wierzchołka łamanej
Ł, który nie jest wyróżniony (patrz Twierdzenie 10.1
w Wykładzie X), jest punktem gładkości granicy minimalnej ![]() .
Innymi słowy, sytuacja (A) daje tylko punkty gładkości granicy
minimalnej. Albo też – patrz Uwaga 15.2 powyżej –
punkty na
.
Innymi słowy, sytuacja (A) daje tylko punkty gładkości granicy
minimalnej. Albo też – patrz Uwaga 15.2 powyżej –
punkty na ![]() , których rzędne są węzłami niewyróżnionymi,
są punktami gładkości granicy minimalnej.
, których rzędne są węzłami niewyróżnionymi,
są punktami gładkości granicy minimalnej.
Co natomiast skrywa się za sytuacją (B) mogącą wystąpić w przebiegu algorytmu, czyli – znowu Uwaga 15.2 – co się skrywa za węzłami wyróżnionymi? By odpowiedzieć, zajmijmy się tą sytuacją szczegółowo.
Ad (B) Teraz w łamanej Ł wierzchołek
![]() ,
, ![]() , sąsiaduje
z bokiem leżącym na ścianie IN, na którym wartości
, sąsiaduje
z bokiem leżącym na ścianie IN, na którym wartości ![]() są
większe od
są
większe od ![]() , oraz z bokiem leżącym
na ścianie
, oraz z bokiem leżącym
na ścianie ![]() , na którym wartości
, na którym wartości ![]() są mniejsze
od
są mniejsze
od ![]() . Wartość
. Wartość ![]() jest węzłem
wyróżnionym w terminologii z Wykładu X.
jest węzłem
wyróżnionym w terminologii z Wykładu X.
Dla tego portfela wierzchołkowego ![]() nie ma jednoznaczności współczynników Lagrange'a
nie ma jednoznaczności współczynników Lagrange'a
![]() i
i ![]() – teoria Blacka się nie stosuje.
Jednak oczywiście można robić przejścia graniczne przy
– teoria Blacka się nie stosuje.
Jednak oczywiście można robić przejścia graniczne przy
![]() analogicznie, jak w sytuacji (A),
dostając, w oznaczeniach z tamtej sytuacji,
analogicznie, jak w sytuacji (A),
dostając, w oznaczeniach z tamtej sytuacji,
| (15.8) |
gdzie ![]() .
I oczywiście też przy
.
I oczywiście też przy ![]() , dostając
analogicznie
, dostając
analogicznie
| (15.9) |
gdzie tym razem ![]() .
Związki (15.8)–(15.9) pokazują zatem, że
.
Związki (15.8)–(15.9) pokazują zatem, że
![]() .
Wobec własności (15.4),
.
Wobec własności (15.4),
| (15.10) |
W istocie jest lepiej. Mianowicie
Stwierdzenie 15.1
![]() .
.
Pokażemy, że dowolna liczba ![]() spełnia
spełnia
| (15.11) |
co łącznie z inkluzją (15.10) zakończy dowód.
Zauważamy w tym celu, że ![]() ,
tzn ściany IN,
,
tzn ściany IN, ![]() są po prostu krawędziami
spotykającymi się w wierzchołku
są po prostu krawędziami
spotykającymi się w wierzchołku ![]() . Istotnie, warunki
niezdegenerowania spełniane przez
. Istotnie, warunki
niezdegenerowania spełniane przez ![]() pociągają, że w
algorytmie przy przejściu
pociągają, że w
algorytmie przy przejściu ![]() wypada tylko jeden
indeks, np
wypada tylko jeden
indeks, np ![]() , oraz przy przejściu
, oraz przy przejściu ![]() wchodzi
też tylko jeden indeks, np
wchodzi
też tylko jeden indeks, np ![]() . Tak więc
. Tak więc ![]() ,
gdzie
,
gdzie ![]() , oraz
, oraz ![]() , gdzie
, gdzie
![]() .
.
Fakt, że ![]() oznacza, że dla
oznacza, że dla
![]() i jakiegoś rzeczywistego współczynnika
i jakiegoś rzeczywistego współczynnika ![]() zachodzi
zachodzi
a więc równość na składowej numer ![]() oraz nieostre nierówności
oraz nieostre nierówności
![]() na wszystkich pozostałych składowych, w szczególności
na składowych nr
na wszystkich pozostałych składowych, w szczególności
na składowych nr ![]() i
i ![]() :
:
| (15.12) |
| (15.13) |
| (15.14) |
Z (15.12) wyznaczamy ![]() i podstawiamy do
nierówności (15.13)–(15.14), dostając
odpowiednio
i podstawiamy do
nierówności (15.13)–(15.14), dostając
odpowiednio
| (15.15) |
| (15.16) |
Pamiętając, że ![]() ,
nierówności (15.15)–(15.16) dają
,
nierówności (15.15)–(15.16) dają
| (15.17) |
Za chwilę okaże się, że nierówności (15.17) są dokładnie
nierównościami (15.11). Policzymy w tym celu wielkość
![]() w teorii Blacka, gdy zbiorem aktywnych
indeksów jest
w teorii Blacka, gdy zbiorem aktywnych
indeksów jest ![]() ,
, ![]() (teoria Blacka w
wymiarze 2). Wtedy portfele Blacka
(teoria Blacka w
wymiarze 2). Wtedy portfele Blacka
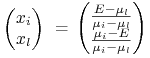 |
mają wariancję
zaś ![]() (porównaj – kolejny raz! – Obserwacja 6.1 w Wykładzie VI). Liczymy
zatem tę pochodną
(porównaj – kolejny raz! – Obserwacja 6.1 w Wykładzie VI). Liczymy
zatem tę pochodną
Następnie, biorąc ![]() , mamy
, mamy
Biorąc natomiast ![]() , mamy
, mamy
Istotnie więc, (15.17) są tożsame z (15.11). Dowód stwierdzenia jest zakończony.
∎Zauważmy, że ze Stwierdzenia 15.1 wynika
| (15.18) |
Jedną szczegółową ilustrację rachunków w tym ostatnim dowodzie (w ramach przykładu Iwanickiego w wymiarze 5 podanego już wcześniej w tym Wykładzie XV) podamy jeszcze później, po pewnym ogólniejszym podsumowaniu.
Pora na rekapitulację. Przeprowadzona powyżej dyskusja
algorytmu CLA pokazała, że w każdej z sytuacji (A) i (B), w opisie
wzajemnych położeń zbiorów ![]() , obok liczb
, obok liczb
![]() zdefiniowanych już jakiś czas
temu wzorem (15.1), ważną – niejako dualną – rolę odgrywają
też liczby
zdefiniowanych już jakiś czas
temu wzorem (15.1), ważną – niejako dualną – rolę odgrywają
też liczby ![]() . Naturalne jest w takiej sytuacji
przyjąć następującą ogólną
. Naturalne jest w takiej sytuacji
przyjąć następującą ogólną
Definicja 15.2
gdzie IN to dowolny z etapów występujących w danej realizacji algorytmu CLA.
(Podkreślamy, że w książce Markowitza [22] wielkości
![]() i
i ![]() definiowane są równocześnie. W tych wykładach – nie. Wiąże się
to ze zbyt mocnymi warunkami niezdegenerowania zakładanymi u
Markowitza. Nasze ,,niezdegenerowane parametry” są
scharakteryzowane słabszymi warunkami; niżej piszemy
o tym szerzej.)
definiowane są równocześnie. W tych wykładach – nie. Wiąże się
to ze zbyt mocnymi warunkami niezdegenerowania zakładanymi u
Markowitza. Nasze ,,niezdegenerowane parametry” są
scharakteryzowane słabszymi warunkami; niżej piszemy
o tym szerzej.)
Po przyjęciu takiego oznaczenia, w sytuacji (A) wzór (15.7) przybiera przejrzystą postać
| (15.19) |
Natomiast w sytuacji (B), równość (15.18) po wprowadzeniu tego nowego symbolu, oznacza
| (15.20) |
oraz
| (15.21) |
Wniosek 15.2
W każdym węźle wyróżnionym ![]() globalna funkcja
globalna funkcja ![]() ma skok w górę równy
ma skok w górę równy
![]() .
Innymi słowy, w sytuacji (B) w opisie przebiegu algorytmu CLA
mamy zawsze punkt załamania granicy minimalnej w aspekcie M.
.
Innymi słowy, w sytuacji (B) w opisie przebiegu algorytmu CLA
mamy zawsze punkt załamania granicy minimalnej w aspekcie M.
Zestawiając ten wniosek z poprzednim Wnioskiem 15.1,
widzimy, że to dokładnie węzły wyróżnione okazują się być rzędnymi
punktów załamania granicy minimalnej, zaś dany skok funkcji
![]() mierzy (co prawda na mniej kanonicznej płaszczyźnie
wariancja – wartość oczekiwana i tylko z dokładnością
do czynnika 2) wielkość takiego załamania.
mierzy (co prawda na mniej kanonicznej płaszczyźnie
wariancja – wartość oczekiwana i tylko z dokładnością
do czynnika 2) wielkość takiego załamania.
Zapamiętajmy ten fakt; to jeden z kilku
kluczowych momentów całego wykładu APRK1.
Uwaga 15.4
Dla każdego zbioru IN pojawiającego się w danej realizacji
algorytmu CLA istnieje poręczna formuła na wielkość
![]() , analogiczna
do formuły (15.1) definiującej
, analogiczna
do formuły (15.1) definiującej
![]() .
Skoro jest to kres górny wartości
.
Skoro jest to kres górny wartości ![]() , przy których
na ścianie IN zachodzą warunki K-KT charakteryzujące portfele
wierzchołkowe, zatem, rozwiązując wiadomy układ liniowych
nierówności dających ograniczenia z góry na
, przy których
na ścianie IN zachodzą warunki K-KT charakteryzujące portfele
wierzchołkowe, zatem, rozwiązując wiadomy układ liniowych
nierówności dających ograniczenia z góry na
![]() ,
,
| (15.22) |
(We wszystkich literach greckich w (15.22) dla
lepszej czytelności opuszczony jest dolny indeks ![]() .
Ponadto, gdy w momencie startu algorytmu
.
Ponadto, gdy w momencie startu algorytmu ![]() i
i ![]() , wtedy ten kres górny
przyjmuje się równy
, wtedy ten kres górny
przyjmuje się równy ![]() ).
).
Z przeprowadzonych dotąd rozważań wynika
Obserwacja. 15.1
![]()
![]() dla każdego
dla każdego ![]() pojawiającego
się w danej realizacji algorytmu CLA.
pojawiającego
się w danej realizacji algorytmu CLA.
![]() Jeśli w realizacji algorytmu CLA po
etapie IN bezpośrednio następuje etap
Jeśli w realizacji algorytmu CLA po
etapie IN bezpośrednio następuje etap ![]() ,
to
,
to ![]() .
.
Punkt ![]() wynika z samego opisu etapów algorytmu CLA.
Natomiast punkt
wynika z samego opisu etapów algorytmu CLA.
Natomiast punkt ![]() , ogniskujący jak w soczewce
całe piękno algorytmu CLA, wynika z równości (15.19),
(15.20) i (15.21). Wzory na
, ogniskujący jak w soczewce
całe piękno algorytmu CLA, wynika z równości (15.19),
(15.20) i (15.21). Wzory na
![]() (patrz (15.1) ) i na
(patrz (15.1) ) i na
![]() (patrz (15.22), gdzie
oczywiście IN trzeba zastąpić przez
(patrz (15.22), gdzie
oczywiście IN trzeba zastąpić przez ![]() ) nie mają na
pierwszy rzut oka nic wspólnego. A jednak zawsze wyrażają te
same wielkości!
) nie mają na
pierwszy rzut oka nic wspólnego. A jednak zawsze wyrażają te
same wielkości!
Jest bardzo pouczające przeanalizować ten punkt ![]() Obserwacji 15.1 powyżej na wybranych fragmentach przebiegu algorytmu
CLA w przykładzie Iwanickiego (już wcześniej przytoczonym).
Obserwacji 15.1 powyżej na wybranych fragmentach przebiegu algorytmu
CLA w przykładzie Iwanickiego (już wcześniej przytoczonym).
Kolejność następowania etapów w tamtym przykładzie jest znana, bo też już była podana wcześniej. I otóż, z przybliżeniem do trzech miejsc dziesiętnych po przecinku,
| (15.23) |
Ta ostatnia równość (15.23) jest szczególnie godna uwagi. Z jednej strony można obliczyć nawet dokładniej, że
Z drugiej strony walory, których wartości oczekiwane sąsiadują z
![]() to: walor drugi (sąsiadowanie z góry,
to: walor drugi (sąsiadowanie z góry, ![]() )
oraz walor czwarty (sąsiadowanie z dołu,
)
oraz walor czwarty (sąsiadowanie z dołu, ![]() ).
Kuszące jest spróbować zastosować poznane wcześniej
(jeszcze w dowodzie Stwierdzenia 15.1) wzory:
).
Kuszące jest spróbować zastosować poznane wcześniej
(jeszcze w dowodzie Stwierdzenia 15.1) wzory:
![]() na
na
![]() , oraz
, oraz ![]() na
na ![]() . W efekcie dostalibyśmy poprawnie
. W efekcie dostalibyśmy poprawnie
lecz także
co już nie jest wartością występującą w (15.23).
Czyżby rozwinięta wcześniej teoria przestawała pracować?
Nic podobnego. Zapomnieliśmy tylko, że w aktualnym
przebiegu CLA w przykładzie Iwanickiego, przed dojściem
do wierzchołka ![]() nie jesteśmy na krawędzi łączącej
go z wierzchołkiem najbliższym w sensie wartości oczekiwanej
(tj na krawędzi
nie jesteśmy na krawędzi łączącej
go z wierzchołkiem najbliższym w sensie wartości oczekiwanej
(tj na krawędzi ![]() ), tylko na krawędzi łączącej
), tylko na krawędzi łączącej
![]() z dalszym w sensie wartości oczekiwanej
wierzchołkiem
z dalszym w sensie wartości oczekiwanej
wierzchołkiem ![]() (por. też (15.23) ).
Po uwzględnieniu tego przeoczenia
(por. też (15.23) ).
Po uwzględnieniu tego przeoczenia
już jak trzeba.
W charakterze komentarza do Obserwacji 15.1 powyżej należy stwierdzić, że słowa ,,pojawiającego się w danej realizacji algorytmu” są w tej obserwacji kluczowe.
![]() Np w znanym nam przykładzie Mordona
[przytaczanym tu od nowa dla wygody czytelnika]
Np w znanym nam przykładzie Mordona
[przytaczanym tu od nowa dla wygody czytelnika]
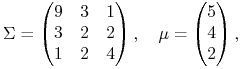 |
na ścianie ![]() , przez którą nie przebiega
łamana wierzchołkowa60 w tym doskonale rozpoznanym
przykładzie przebieg algorytmu CLA to
, przez którą nie przebiega
łamana wierzchołkowa60 w tym doskonale rozpoznanym
przykładzie przebieg algorytmu CLA to ![]() wielkości
wielkości ![]() i
i ![]() nabierają zaskakujących
znaczeń. Dokładniej, wzory z Wykładu XIV dają formalnie
na tej ścianie
nabierają zaskakujących
znaczeń. Dokładniej, wzory z Wykładu XIV dają formalnie
na tej ścianie
Zatem, liczone czysto formalnie, ![]() ,
,
Pouczające jest porównać to z pochodną funkcji ![]() na tym
boku. Tutaj
na tym
boku. Tutaj ![]() oraz
oraz
![]() ,
, ![]() . Prowadzi to do
. Prowadzi to do
To wyrażenie jest równe ![]() tylko przy
tylko przy ![]() , a więc
tylko w wierzchołku
, a więc
tylko w wierzchołku ![]() sympleksu
sympleksu ![]() (leżącym w
domknięciu ściany, której dotyczą tu obliczenia).
Zatem wirtualne współczynniki
(leżącym w
domknięciu ściany, której dotyczą tu obliczenia).
Zatem wirtualne współczynniki ![]() wychwytują ten jeden jedyny
portfel na boku
wychwytują ten jeden jedyny
portfel na boku ![]() , który a) jest wierzchołkowy (tj leży
na łamanej Ł) i b) w obrazie którego styczna do obrazu boku
, który a) jest wierzchołkowy (tj leży
na łamanej Ł) i b) w obrazie którego styczna do obrazu boku
![]() jest tożsama ze styczną do granicy minimalnej.
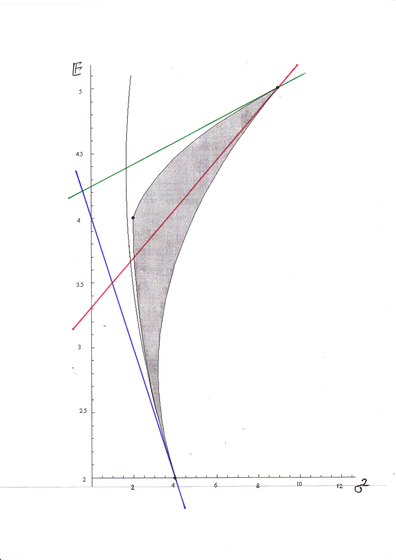
Na rysunku poniżej, na – uwaga – płaszczyźnie
jest tożsama ze styczną do granicy minimalnej.
Na rysunku poniżej, na – uwaga – płaszczyźnie ![]() ,
ta wspólna styczna w punkcie
,
ta wspólna styczna w punkcie ![]() jest
niebieska, natomiast w punkcie
jest
niebieska, natomiast w punkcie ![]() :
styczna do granicy minimalnej jest zielona, zaś styczna do
obrazu boku
:
styczna do granicy minimalnej jest zielona, zaś styczna do
obrazu boku ![]() jest czerwona. [W wersji pdf rysunek
trafia na następną stronę.]
jest czerwona. [W wersji pdf rysunek
trafia na następną stronę.]
Ćwiczenie 15.2 (kontrolne)
Czy czytelnik umie policzyć, na jakich dokładnie wysokościach
narysowane tu styczne przecinają pionową oś zmiennej ![]() ?
?
![]() Jeszcze ciekawszy efekt może wystąpić na ścianie,
której podprzestrzeń afiniczną (rozpinaną przez tę ścianę)
łamana Ł w ogóle omija. Dzieje się tak np w wymiarze 5
ze ścianą
Jeszcze ciekawszy efekt może wystąpić na ścianie,
której podprzestrzeń afiniczną (rozpinaną przez tę ścianę)
łamana Ł w ogóle omija. Dzieje się tak np w wymiarze 5
ze ścianą ![]() w modelu z parametrami
w modelu z parametrami
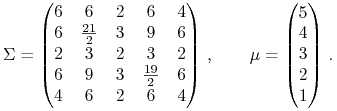 |
Czysto formalnie, wzory z Wykładu XIV dawałyby na tej ścianie
A zatem, dalej czysto formalnie, byłoby
![]() , oraz
, oraz
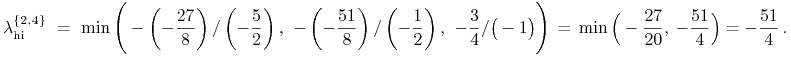 |
W tym przykładzie ściana ![]() okazuje się bardzo
nieoptymalna z punktu widzenia relatywnego minimalizowania
ryzyka w modelu i dla wirtualnych wielkości z algorytmu
z nią związanych mamy
okazuje się bardzo
nieoptymalna z punktu widzenia relatywnego minimalizowania
ryzyka w modelu i dla wirtualnych wielkości z algorytmu
z nią związanych mamy ![]() .61Warto zwrócić uwagę,
że ograniczenia na
.61Warto zwrócić uwagę,
że ograniczenia na ![]() pochodzące od dodatniości
współrzędnych
pochodzące od dodatniości
współrzędnych ![]() -owych podlegają teorii użytej w dowodzie
Stwierdzenia 15.1, i monotoniczność ograniczeń
pochodzących od tych współrzędnych jest zachowywana:
-owych podlegają teorii użytej w dowodzie
Stwierdzenia 15.1, i monotoniczność ograniczeń
pochodzących od tych współrzędnych jest zachowywana:
Te ograniczenia są jednak przesłonięte mocniejszymi
ograniczeniami pochodzącymi od hipotetycznej nieujemności
składowych wektora
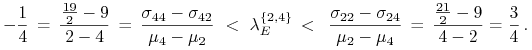
![]() – tej kwintesencji optymalności.
I właśnie nieujemność
– tej kwintesencji optymalności.
I właśnie nieujemność ![]() jest nie do zrealizowania
na boku
jest nie do zrealizowania
na boku ![]() .
.
Podsumowanie algorytmu CLA.
Podczas dyskusji algorytmu CLA wydzieliśmy dwie sytuacje – dwa możliwe rodzaje przejść między kolejnymi etapami algorytmu, przy przyjętych przez nas założeniach niezdegenerowania (15.2).
Po pierwsze
(A). ![]() , gdzie
, gdzie
![]() .
.
Jak wiemy, zbiory IN oraz ![]() różnią się wtedy tylko
jednym elementem, zaś parametr
różnią się wtedy tylko
jednym elementem, zaś parametr ![]() zmienia się płynnie
przy przejściu łamanej wierzchołkowej
zmienia się płynnie
przy przejściu łamanej wierzchołkowej ![]() ze ściany IN na ścianę
ze ściany IN na ścianę ![]() . Dokładniej,
. Dokładniej,
![]() przechodzi przy takim przejściu przez wartość
przechodzi przy takim przejściu przez wartość
![]() (odpowiadający temu węzeł – wartość
(odpowiadający temu węzeł – wartość ![]() jest
niewyróżniony, Wniosek 15.1 powyżej).
jest
niewyróżniony, Wniosek 15.1 powyżej).
Po drugie
(B). ![]()
Wiemy, że wtedy oba zbiory IN oraz ![]() są
dwuelementowe i oba są – różnymi! – nadzbiorami singletonu
są
dwuelementowe i oba są – różnymi! – nadzbiorami singletonu
![]() . W tej fazie algorytmu łamana wierzchołkowa biegnie po
krawędzi IN, wpada w wierzchołek
. W tej fazie algorytmu łamana wierzchołkowa biegnie po
krawędzi IN, wpada w wierzchołek ![]() , zaś po chwili wybiega z
niego po krawędzi
, zaś po chwili wybiega z
niego po krawędzi ![]() . Jeśli chodzi o parametr
. Jeśli chodzi o parametr ![]() ,
to na boku łamanej
,
to na boku łamanej ![]() będącym częścią lub
całą krawędzią IN, zmniejsza się on (będąc cały czas związany
zależnością z Obserwacji 6.1 ze stycznymi do obrazów punktów
na boku IN) do swego kresu dolnego
będącym częścią lub
całą krawędzią IN, zmniejsza się on (będąc cały czas związany
zależnością z Obserwacji 6.1 ze stycznymi do obrazów punktów
na boku IN) do swego kresu dolnego
![]() — gdy punkt bieżący na tym boku dobiega do wierzchołka
— gdy punkt bieżący na tym boku dobiega do wierzchołka ![]() .
Następnie parametr obniża się dalej, teraz parametryzując tylko
nadstyczne położenia prostych podpierających granicę
minimalną w obrazie wierzchołka
.
Następnie parametr obniża się dalej, teraz parametryzując tylko
nadstyczne położenia prostych podpierających granicę
minimalną w obrazie wierzchołka ![]() , który jest, jak wiemy,
punktem załamania tej granicy. (Odpowiadający temu węzeł
– wartość
, który jest, jak wiemy,
punktem załamania tej granicy. (Odpowiadający temu węzeł
– wartość ![]() jest wyróżniony, Wniosek 15.2
powyżej.)
jest wyróżniony, Wniosek 15.2
powyżej.)
Parametr ![]() przebiega tak cały przedział
przebiega tak cały przedział ![]() aż do jego lewego końca
aż do jego lewego końca ![]() . W tym momencie prosta
podpierająca staje się znowu styczna – tym razem do obrazu
krawędzi
. W tym momencie prosta
podpierająca staje się znowu styczna – tym razem do obrazu
krawędzi ![]() . Dalsze zmniejszanie
. Dalsze zmniejszanie ![]() to
parametryzowanie boku łamanej
to
parametryzowanie boku łamanej ![]() będącego
częścią lub całą krawędzią
będącego
częścią lub całą krawędzią ![]() , znowu zgodnie z
zależnością z Obserwacji 6.1 w Wykładzie VI.
, znowu zgodnie z
zależnością z Obserwacji 6.1 w Wykładzie VI.
Uwaga. Przypomnianego tu w (B) opisu zbioru ![]() (patrz
Stwierdzenie 15.1 powyżej) wykładowca nie znalazł
w dostępnej literaturze. Został on włączony do wykładów
dopiero w roku akademickim 2009/10.
(patrz
Stwierdzenie 15.1 powyżej) wykładowca nie znalazł
w dostępnej literaturze. Został on włączony do wykładów
dopiero w roku akademickim 2009/10.
Podany opis przebiegu algorytmu CLA obowiązuje, powtarzamy to, przy założeniu warunków niezdegenerowania (15.2). Zauważmy jednak na koniec, że można podać równoległy zestaw innych warunków, też pociągający ten sam przebieg algorytmu, tzn występowanie w jego realizacji tylko sytuacji typu (A) oraz (B), co prawda przebieganych w przeciwnym porządku i kierunkach, niż poprzednio. Mianowicie, jeśli zakładać tylko, że
| (15.24) |
wtedy łamaną wierzchołkową ![]() można odzyskiwać
od końca do początku: od
można odzyskiwać
od końca do początku: od ![]() (i
(i ![]() )
do
)
do ![]() (i
(i ![]() ). W dyskusji jej przebiegu,
w pełni
analogicznej do tej przedstawionej w Wykładzie XV, akcentuje się
wtedy tylko progowe wartości
). W dyskusji jej przebiegu,
w pełni
analogicznej do tej przedstawionej w Wykładzie XV, akcentuje się
wtedy tylko progowe wartości ![]() ,
IN – ściany aktywne, goszczące łamaną
,
IN – ściany aktywne, goszczące łamaną ![]() .
Warunki (15.24) gwarantują wtedy z naddatkiem brak kolizji
przy zmianach ścian. Zatem
.
Warunki (15.24) gwarantują wtedy z naddatkiem brak kolizji
przy zmianach ścian. Zatem ![]() wygląda wtedy
tak samo jak przy obowiązywaniu warunków (15.2): doznaje
tylko ewolucji typu (A) i/lub (B). Podkreślamy jeszcze raz,
że każdy z zestawów warunków (15.2) i (15.24)
sam w sobie jest słabszy niż ten, który podany jest na
stronie 161 w [22].
wygląda wtedy
tak samo jak przy obowiązywaniu warunków (15.2): doznaje
tylko ewolucji typu (A) i/lub (B). Podkreślamy jeszcze raz,
że każdy z zestawów warunków (15.2) i (15.24)
sam w sobie jest słabszy niż ten, który podany jest na
stronie 161 w [22].
Można zauważyć na koniec, że tak właśnie, na samym początku, w [19] Markowitz planował znajdować wszystkie portfele efektywne: zaczynać od portfela mającego minimum wariancji, natomiast kończyć na portfelu mającym maksimum wartości oczekiwanej. Można to dokładnie prześledzić w tekście na Rysunku 14.2 (reprodukcja strony 87 z [19]) w Wykładzie XIV.