2. Wykład II, 9.X.2009
Co wiemy na temat rzeczywistych rozkładów zmiennych stóp zwrotu?
Najczęściej nie wiemy nic konkretnego na temat rozkładów zmiennych stóp zwrotu z akcji spółek notowanych na giełdzie. Markowitz był tego świadom od samego początku. Na stronie 82 w swoim podstawowym artykule [19] pisał
… Perhaps there are ways, by combining statistical techniques and the
judgment of experts, to form reasonable probability beliefs ![]() .
We could use these beliefs to compute the attainable efficient combinations
of
.
We could use these beliefs to compute the attainable efficient combinations
of ![]() . The investor, being informed of what
. The investor, being informed of what ![]() combinations
were attainable, could state which he desired. We could then find
the portfolio which gave this desired combination.
combinations
were attainable, could state which he desired. We could then find
the portfolio which gave this desired combination.
(Początkową część tego cytatu czytelnik znajdzie też dalej
w tych wykładach – na Rysunku 7.2 w Wykładzie VII, gdzie
strona 82 została trochę ucięta przy skanowaniu.)
Natomiast całą pracę [19] kończył Markowitz takimi oto uwagami, rozwijającymi i ukonkretniającymi te wcześniejsze.1To quasi-powtórzenie pokazuje, jaką wagę przykładał on do zagadnienia znalezienia właściwych parametrów w analizie portfelowej.
To use the ![]() -
-![]() rule in the selection of securities
we must have procedures for finding reasonable
rule in the selection of securities
we must have procedures for finding reasonable ![]() and
and ![]() .
These procedures, I believe, should combine statistical techniques and
the judgment of practical men. My feeling is that the statistical
computations should be used to arrive at a tentative set of
.
These procedures, I believe, should combine statistical techniques and
the judgment of practical men. My feeling is that the statistical
computations should be used to arrive at a tentative set of ![]() and
and ![]() . Judgment should then be used in increasing or decreasing
some of these
. Judgment should then be used in increasing or decreasing
some of these ![]() and
and ![]() on the basis of factors or nuances
not taken into account by the formal computations. Using this revised
set of
on the basis of factors or nuances
not taken into account by the formal computations. Using this revised
set of ![]() and
and ![]() , the set of efficient
, the set of efficient ![]() combinations
could be computed, the investor could select the combination he preferred,
and the portfolio which gave rise to this
combinations
could be computed, the investor could select the combination he preferred,
and the portfolio which gave rise to this ![]() combination could be
found.
combination could be
found.
One suggestion as to tentative ![]() and
and ![]() is to use
the observed
is to use
the observed ![]() ,
, ![]() for some period of the past. I believe
that better methods, which take into account more information, can be
found. I believe that what is needed is essentially a ,,probabilistic”
reformulation of security analysis. I will not pursue this subject here,
for this is ,,another story”. It is a story of which I have read only
the first page of the first chapter.
for some period of the past. I believe
that better methods, which take into account more information, can be
found. I believe that what is needed is essentially a ,,probabilistic”
reformulation of security analysis. I will not pursue this subject here,
for this is ,,another story”. It is a story of which I have read only
the first page of the first chapter.
Zgodnie z sugestią Markowitza zawartą w drugim akapicie powyższego cytatu, estymujemy zatem podstawowe parametry takich zmiennych stóp zwrotu, używając estymatorów z jednakowymi (mówi się też: jednorodnymi) wagami, jak w przykładach w Wykładzie I.
Realnie zmienne losowe w analizie portfelowej mogą mieć najrozmaitsze rozkłady. Oto pewna para takich rozkładów, pojawiająca się w obecnie już klasycznym przykładzie ,,5 stanów giełdy” (pochodzącym z dawniejszych wykładów [13] profesora Krzyżewskiego na Wydziale MIM UW; przykładzie wtedy przesuniętym na ćwiczenia, a teraz analizowanym tutaj aż do Rysunku 2.1 włącznie, z niespodziewanym nawrotem do niego jeszcze w Przykładzie 3.3 w Wykładzie III):
| stan | prawdopodobieństwo wystąpienia | ||
| hossa | |||
| wzrost | |||
| stabilizacja | |||
| spadek | |||
| bessa |
Wartości zmiennych losowych ![]() i
i ![]() to stopy
wzrostu (które mogą też być ujemne) notowań spółek A i B w zaproponowanych
tu możliwych stanach giełdy, w ustalonym okresie inwestycyjnym.
to stopy
wzrostu (które mogą też być ujemne) notowań spółek A i B w zaproponowanych
tu możliwych stanach giełdy, w ustalonym okresie inwestycyjnym.
Na podstawie tak podanych danych surowych tworzymy tabelę rozkładu
łącznego zestawu zmiennych ![]() , albo,
jak niektórzy wolą powiedzieć, tabelę rozkładu zmiennej losowej
dwuwymiarowej.
, albo,
jak niektórzy wolą powiedzieć, tabelę rozkładu zmiennej losowej
dwuwymiarowej.
Następnie obliczamy podstawowe parametry rozkładów zmiennych
![]() i
i ![]() (tj rozkładów brzegowych wspomnianej
zmiennej losowej dwuwymiarowej):
(tj rozkładów brzegowych wspomnianej
zmiennej losowej dwuwymiarowej):
Uwaga 2.1
W dwóch przykładach w Wykładzie I mogliśmy tylko policzyć estymatory
tych parametrów dla zmiennych stóp zwrotu ![]() oraz
oraz ![]() ; rozkładów tamtych zmiennych nie
znaliśmy. Dzięki estymatorom policzonym dla pierwszej pary tamtych
zmiennych mogliśmy m. in. dopracować się wykresu podanego na
Rysunku 1.2 w Wykładzie I.
; rozkładów tamtych zmiennych nie
znaliśmy. Dzięki estymatorom policzonym dla pierwszej pary tamtych
zmiennych mogliśmy m. in. dopracować się wykresu podanego na
Rysunku 1.2 w Wykładzie I.
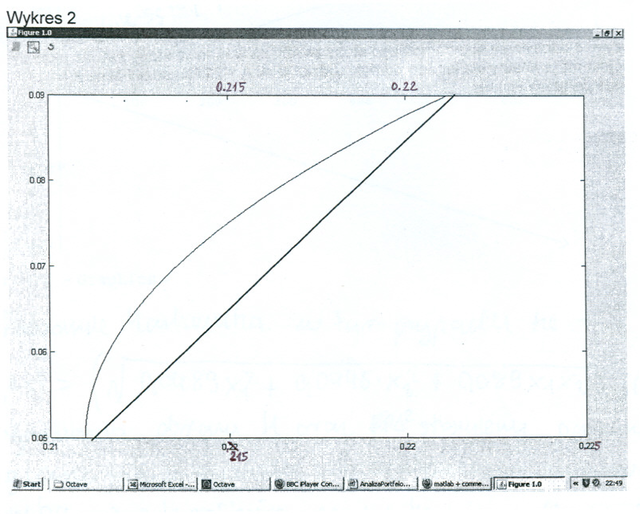
Teraz zmienne losowe znamy dokładnie. Postawmy pytanie, jak w przykładzie
,,5 stanów giełdy” wygląda analogiczny do tamtego wykres na płaszczyźnie
![]() ?
?
(Dla nas na tym wykresie ważny jest tylko zaznaczony łuk hiperboli. Znaczenie odcinka prostej widocznego poniżej łuku hiperboli znane jest tylko studentowi – autorowi wykresu.)
Wprowadzimy teraz cały zestaw oznaczeń ogólnie przyjętych w teorii Markowitza [19, 21, 22] – tzw. Markowitz setup:
-
Ilość spółek notowanych na giełdzie oznaczamy
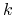 .
.
-
Zmienne losowe – stopy zwrotu z notowań tych spółek w ustalonym okresie inwestycyjnym oznaczamy
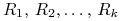 .
Są to zmienne losowe na tej samej (bliżej nie precyzowanej, por.
powyższy długi cytat z pracy Markowitza) przestrzeni probabilistycznej,
przyjmujące wartości z
.
Są to zmienne losowe na tej samej (bliżej nie precyzowanej, por.
powyższy długi cytat z pracy Markowitza) przestrzeni probabilistycznej,
przyjmujące wartości z 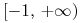 , o których zawsze będziemy
zakładać, że ich wartości oczekiwane
, o których zawsze będziemy
zakładać, że ich wartości oczekiwane 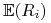 oraz wariancje
oraz wariancje
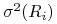 ,
, 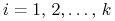 , są wszystkie skończone.
, są wszystkie skończone.
-
Będziemy pisali krótko:
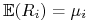 ,
,
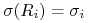 ,
, 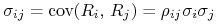 , gdzie
, gdzie 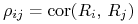 dla
dla 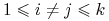 .
.
-
Wektor wartości oczekiwanych
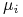 oznaczamy
oznaczamy
![\mu=[\mu _{i}]_{{i=1}}^{k}](wyklady/pk1/mi/mi221.png) , zaś wektor zmiennych losowych
, zaś wektor zmiennych losowych
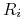 oznaczamy
oznaczamy ![R=[R_{i}]_{{i=1}}^{k}](wyklady/pk1/mi/mi211.png) .
.
-
Będziemy mówić, że wektorowa zmienna losowa
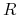 ma wektorową
wartość oczekiwaną
ma wektorową
wartość oczekiwaną 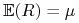 . Wektor odchyleń standardowych
będziemy (czasem) oznaczać
. Wektor odchyleń standardowych
będziemy (czasem) oznaczać ![\sigma=[\sigma _{i}]_{{i=1}}^{k}](wyklady/pk1/mi/mi170.png) .
.
-
Wreszcie macierz kowariancji wektorowej zmiennej losowej
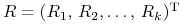 oznaczamy
oznaczamy![\Sigma=\left[\begin{array}[]{cccc}\sigma _{1}^{{\, 2}}&&&\\
&\sigma _{2}^{{\, 2}}&\sigma _{{ij}}&\\
&\sigma _{{ij}}&\ddots&\\
&&&\sigma _{k}^{{\, 2}}\end{array}\right]=\left[\begin{array}[]{cccc}\sigma _{1}^{{\, 2}}&&&\\
&\sigma _{2}^{{\, 2}}&\rho _{{ij}}\sigma _{i}\sigma _{j}&\\
&\rho _{{ij}}\sigma _{i}\sigma _{j}&\ddots&\\
&&&\sigma _{k}^{{\, 2}}\end{array}\right].](wyklady/pk1/mi/mi212.png)
-
Teoria, którą będziemy poznawać na tych wykładach, nie jest (o ile ktoś miałby jeszcze co do tego wątpliwości) oderwana od życia. Oto – dla ilustracji tej tezy – treść ulotki banku ING BSK z roku 2009, reklamującej pewien nowy produkt banku: ,, Na wysokość wypłaty na koniec programu wpływa wzrost wartości portfela inwestycyjnego. Strategia inwestycyjna została oparta na innowacyjnym modelu matematycznym, który zdobył nagrodę Nobla (Markowitz Efficient Frontier Theory). Jego unikalność polega na tym, że generuje stabilne dochody zarówno na rynkach wzrostowych, jak i spadkowych.”
-
W Wykładzie I (Rysunek 1.1) dowiedzieliśmy się, jak fundusz wielkiego inwestora Warrena Buffetta ,,bije” (w długim i trudnym okresie czasu 2006 - 2010 obejmującym kryzys finansowy lat 2008-9) amerykańską giełdę. W naszym kraju też zdarzają się godne uwagi osiągnięcia na podobnym polu. Dokładniej, w pierwszej połowie roku 2010, w V Mistrzostwach Polski Inwestorów, zwycięzca w kategorii akcje (pan Andrzej Laskowski z Redy) zwiększył wartość swojego portfela aż o 78
 .
.
Obserwacja. 2.1
Dowód wynika wprost z wcześniej podanych (i znanych już z wykładu RP 1) definicji.
Przykład 2.1
W przykładzie ,,5 stanów giełdy”, wobec obliczeń
zrobionych już wcześniej, wektor ![]() i macierz
i macierz ![]() to
to
Przypomnienie. Kryterium Sylvestera, poznane na I roku
na wykładach z GALu, wyjaśnia, kiedy macierz ![]() rzeczywista
i symetryczna wymiaru
rzeczywista
i symetryczna wymiaru ![]() jest dodatnio określona:
jest dodatnio określona:
gdzie ![]() to minor
to minor ![]() w macierzy
w macierzy ![]() używający
wierszy o numerach
używający
wierszy o numerach ![]() oraz kolumn o numerach
oraz kolumn o numerach
![]() (używamy tu oznaczeń ze zbyt mało w Polsce
znanego podręcznika z teorii macierzy i algebry liniowej [6]).
Minory
(używamy tu oznaczeń ze zbyt mało w Polsce
znanego podręcznika z teorii macierzy i algebry liniowej [6]).
Minory ![]() w kryterium Sylvestera to minory główne macierzy
w kryterium Sylvestera to minory główne macierzy ![]() .
.
Znane jest też podobne kryterium na temat nieujemnej określoności
macierzy, aczkolwiek nie wchodzi ono do standardowego kursu GALu.
Mianowicie, dla macierzy ![]() , kwadratowej
, kwadratowej ![]() rzeczywistej symetrycznej,
rzeczywistej symetrycznej,
przy wszystkich ![]() . Minory
. Minory ![]() to minory
centralne macierzy
to minory
centralne macierzy ![]() .
.
To nowe kryterium jest w istocie dość szybkim wnioskiem z kryterium Sylvestera – patrz [6], strona 270. Kluczowe miejsce w rozumowaniu, aczkolwiek piękne, jest tam jednak zredagowane niezmiernie lakonicznie. Dla wygody czytelnika, poniżej przytaczamy właściwy fragment wspomnianej strony z [6].
(W rozwinięciu ![]() minora centralnego
minora centralnego
![]() występują wyrazy z nieujemnymi współczynnikami przy potęgach
występują wyrazy z nieujemnymi współczynnikami przy potęgach
![]() — dlaczego?)
— dlaczego?)
W tej chwili mamy już język, lecz jest on jeszcze dla nas martwą
literą. Jak Markowitz koduje, czy modeluje, swoje portfele?
Wskazówki dostarcza już Wykład 1, gdzie co prawda występują
tylko dwie spółki, zaś portfele opisywane są punktami ![]() leżącymi
na prostej
leżącymi
na prostej ![]() w pierwszej ćwiartce (czyli spełniającymi
warunki
w pierwszej ćwiartce (czyli spełniającymi
warunki ![]() i
i ![]() ). Ze swojego kapitału
). Ze swojego kapitału ![]() ,
inwestor przeznaczał tam
,
inwestor przeznaczał tam ![]() na zakup akcji pierwszej spółki
(i kupował tych akcji
na zakup akcji pierwszej spółki
(i kupował tych akcji ![]() ) oraz
) oraz
![]() na zakup akcji drugiej spółki (których kupował
na zakup akcji drugiej spółki (których kupował
![]() ).
).
Teraz, gdy dostępne są akcje spółek o numerach ![]() ,
inwestor dzieli swój kapitał
,
inwestor dzieli swój kapitał ![]() na części
na części
gdzie oczywiście ![]() oraz
oraz ![]() . Następnie, dla
. Następnie, dla ![]() ,
za kwotę
,
za kwotę ![]() kupuje on akcje spółki numer
kupuje on akcje spółki numer ![]() .
.
Możliwe portfele inwestora są więc teraz opisywane punktami
![x=\left(\begin{array}[]{c}x_{1}\\
x_{2}\\
\vdots\\
x_{k}\end{array}\right)\in\mathbb{R}^{k}](wyklady/pk1/mi/mi193.png) |
takimi, że ![]() oraz
oraz ![]() .
.
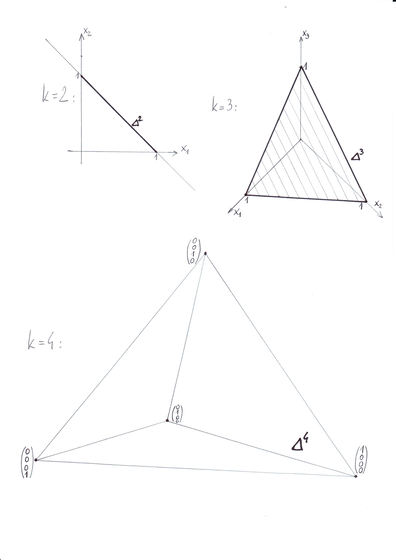
Zbiór wszystkich takich punktów oznaczamy symbolem ![]() ,
,
![]() . Jest to tzw. sympleks standardowy
w
. Jest to tzw. sympleks standardowy
w ![]() [w wersji pdf Rysunek 2.3 wypada dopiero na następnej stronie]:
[w wersji pdf Rysunek 2.3 wypada dopiero na następnej stronie]:
W Wykładzie I widzieliśmy, że zainwestowanie własnego kapitału w akcje
spółek A i B, opisane (czy zakodowane) portfelem ![]() ma stopę zwrotu (lub, krócej: taki portfel ma stopę zwrotu)
ma stopę zwrotu (lub, krócej: taki portfel ma stopę zwrotu)
![]() .2To w dalszym ciągu jest
zmienna losowa! Czy analogicznie jest gdy inwestuje się kapitał w
akcje
.2To w dalszym ciągu jest
zmienna losowa! Czy analogicznie jest gdy inwestuje się kapitał w
akcje ![]() spółek? Tzn czy w dalszym ciągu ma miejsce odpowiedniość
spółek? Tzn czy w dalszym ciągu ma miejsce odpowiedniość
| (2.1) |
wiążąca dany portfel Markowitza ze zmienną losową stojącą po prawej stronie w (2.1) jako jego stopą zwrotu ?
Tak jest w istocie. Jeżeli przez ![]() oznaczymy kapitał inwestora, wtedy
oznaczymy kapitał inwestora, wtedy
![]() będzie kwotą przeznaczoną przez niego na zakup akcji spółki
numer
będzie kwotą przeznaczoną przez niego na zakup akcji spółki
numer ![]() . Jeśli
. Jeśli ![]() i
i ![]() oznaczają
notowania akcji
oznaczają
notowania akcji ![]() -tej spółki odpowiednio na początku i na końcu okresu
inwestycyjnego (pamiętamy, że ta druga wielkość jest zmienną losową) oraz
-tej spółki odpowiednio na początku i na końcu okresu
inwestycyjnego (pamiętamy, że ta druga wielkość jest zmienną losową) oraz
![]() jest ilością nabytych przez inwestora
akcji
jest ilością nabytych przez inwestora
akcji ![]() -tej spółki, wtedy jego portfel
-tej spółki, wtedy jego portfel ![]() ma łącznie stopę zwrotu
ma łącznie stopę zwrotu
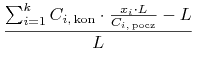 |
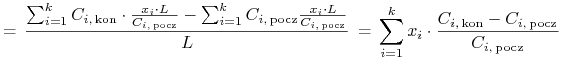 |
||
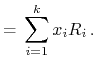 |
To spostrzeżenie motywuje następującą
Definicja 2.1
Dla każdego portfela Markowitza ![]()
-
(i) Wartością oczekiwaną portfela
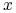 , oznaczaną
, oznaczaną 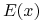 ,
nazywamy wartość oczekiwaną zmiennej stopy zwrotu przy inwestowaniu
w ten portfel, czyli zmiennej losowej stojącej po prawej stronie
w (2.1):
,
nazywamy wartość oczekiwaną zmiennej stopy zwrotu przy inwestowaniu
w ten portfel, czyli zmiennej losowej stojącej po prawej stronie
w (2.1): 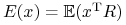 .
.
-
(ii) Odchyleniem standardowym (względnie wariancją) portfela
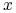 ,
oznaczanym
,
oznaczanym 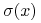 (
( 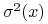 ), nazywamy odchylenie
standardowe (wariancję) zmiennej losowej
), nazywamy odchylenie
standardowe (wariancję) zmiennej losowej 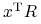 :
:
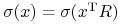 (
( 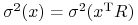 ).
).
Obserwacja. 2.2
-
(i)
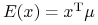 dla
dla 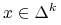 .
. -
(ii)
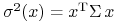 dla
dla 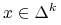 .
. -
(iii) Macierz
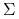 jest nieujemnie określona i
jest nieujemnie określona i 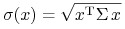 dla
dla 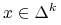 .
.
-
(i)
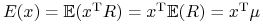 ,
,
-
(ii)
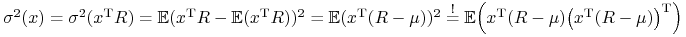
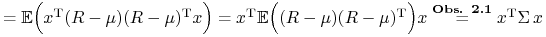 .
.
-
(iii) Dowolnie ustalamy
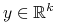 i rozważamy zmienną losową
i rozważamy zmienną losową
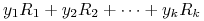 niezwiązaną ściśle z analizą
portfelową. Powtarzając rachunki z dowodu (ii) (w którym nie wykorzystaliśmy
założenia
niezwiązaną ściśle z analizą
portfelową. Powtarzając rachunki z dowodu (ii) (w którym nie wykorzystaliśmy
założenia 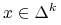 ),
),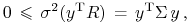
zaś wzór na
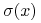 dla
dla 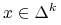 wynika z już udowodnionej części (ii).
wynika z już udowodnionej części (ii).
W teorii Markowitza kluczową rolę odgrywa odwzorowanie Markowitza
![]() :
:
![\Delta^{k}\ni x\longmapsto\mathcal{M}(x)=\left(\begin{array}[]{c}\sigma(x)\\
E(x)\end{array}\right)=\left(\begin{array}[]{c}\sqrt{x^{{\text{T}}}\Sigma\, x}\\
\mu^{{\text{T}}}x\end{array}\right)\in\mathbb{R}^{2}(\sigma,\, E).](wyklady/pk1/mi/mi188.png) |
Często używane też jest zmodyfikowane odwzorowanie Markowitza
![]() :
:
Uwaga 2.2
-
a) W oryginalnych pracach Markowitza (i tylko Markowitza) kolejność zmiennych jest odwrócona:
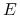 jest odkładana na osi odciętych,
natomiast
jest odkładana na osi odciętych,
natomiast 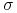 (względnie
(względnie 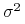 ) – na osi rzędnych. Oczywiście
sam Markowitz nie nazywał tak tych odwzorowań. Mówił on tylko o `attainable
) – na osi rzędnych. Oczywiście
sam Markowitz nie nazywał tak tych odwzorowań. Mówił on tylko o `attainable
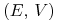 combinations' – patrz np strona 82 w [19]. Powyższe
nazwy i sam symbol
combinations' – patrz np strona 82 w [19]. Powyższe
nazwy i sam symbol 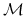 wprowadził, być może nie jako jedyny
na świecie, Krzyżewski w [13].
wprowadził, być może nie jako jedyny
na świecie, Krzyżewski w [13].
-
b) W późniejszej części teorii, którą poznaje się na wykładach z analizy portfelowej, odwzorowania
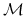 i
i 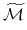 będą miały o wiele większą dziedzinę
będą miały o wiele większą dziedzinę
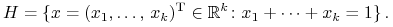
(2.2) Będzie to więc hiperpłaszczyzna afinicznie rozpięta przez sympleks standardowy
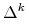 (oczywiście
(oczywiście 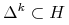 ). Okaże się przy tym,
że odwzorowania
). Okaże się przy tym,
że odwzorowania 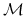 i
i 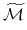 idące z
idące z 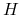 zachowują
swoje wzory definicyjne z podejścia Markowitza! Patrząc na to z innej strony,
tylko przez jakiś czas zajmować się będziemy wyłącznie portfelami Markowitza
leżącymi w sympleksach standardowych
zachowują
swoje wzory definicyjne z podejścia Markowitza! Patrząc na to z innej strony,
tylko przez jakiś czas zajmować się będziemy wyłącznie portfelami Markowitza
leżącymi w sympleksach standardowych 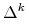 i (tym samym) mającymi
wszystkie współrzędne nieujemne.
i (tym samym) mającymi
wszystkie współrzędne nieujemne.
-
c) Obraz
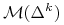 będziemy nazywali
zbiorem osiągalnym (niektórzy mówią też: zbiór możliwości)
w teorii Markowitza. Podobnie,
będziemy nazywali
zbiorem osiągalnym (niektórzy mówią też: zbiór możliwości)
w teorii Markowitza. Podobnie, 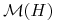 będzie zbiorem osiągalnym
w tej sygnalizowanej w b) szerszej teorii, która później włączy w siebie
teorię Markowitza.
będzie zbiorem osiągalnym
w tej sygnalizowanej w b) szerszej teorii, która później włączy w siebie
teorię Markowitza.
Ćwiczenie 2.1
Uzasadnić, że punkt ![]() i pięć innych
punktów powstających z niego przez wszelkie możliwe permutacje
współrzędnych, leżą wszystkie na jednej płaszczyźnie (inaczej
mówiąc: wymienione punkty są współpłaszczyznowe).
i pięć innych
punktów powstających z niego przez wszelkie możliwe permutacje
współrzędnych, leżą wszystkie na jednej płaszczyźnie (inaczej
mówiąc: wymienione punkty są współpłaszczyznowe).
Ćwiczenie 2.2 (nie takie natychmiastowe)
Na płaszczyźnie ![]() zdefiniowanej w (2.2) przy
zdefiniowanej w (2.2) przy ![]() rozważamy prostą
rozważamy prostą ![]() oraz prostą
oraz prostą
![]() ; nie wszystkie współczynniki
; nie wszystkie współczynniki ![]() są sobie
równe. Wyznaczyć odległość tych prostych jako podzbiorów przestrzeni
są sobie
równe. Wyznaczyć odległość tych prostych jako podzbiorów przestrzeni ![]() wyposażonej w metrykę euklidesową.
wyposażonej w metrykę euklidesową.
Ta odległość jest niemniejsza (najczęściej większa) niż odległość
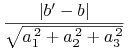 |
odpowiednich płaszczyzn w ![]() .
.
Jaki wektor wyznacza kierunek obu tych prostych? Oczywiście iloczyn wektorowy
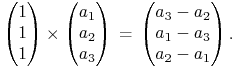 |
Z kolei, jaki wektor jest równoległy do ![]() i prostopadły do obu tych prostych?
Oczywiście
i prostopadły do obu tych prostych?
Oczywiście
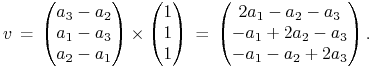 |
Za chwilę przyda się też jego długość
![]() .
.
Ile tego wektora przenosi pierwszą prostą z zadania na drugą? Taka wielokrotność
![]() , że
, że ![]() , czyli w postaci rozwiniętej
, czyli w postaci rozwiniętej
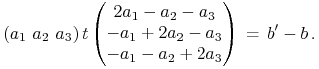 |
Stąd po krótkim rachunku
(długość wektora ![]() jest już wyznaczona wcześniej).
Tak więc szukana odległość prostych to
jest już wyznaczona wcześniej).
Tak więc szukana odległość prostych to
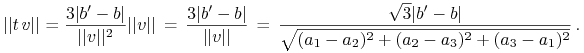 |
Ćwiczenie 2.3
Kiedy odległość prostych z Ćwiczenia 2.2 (wycinanych na ![]() przez płaszczyzny
o podanych równaniach) jest równa odległości samych płaszczyzn
przez płaszczyzny
o podanych równaniach) jest równa odległości samych płaszczyzn
![]() i
i ![]() ?
?
Okazuje się, że aby tak było, współczynniki ![]() winny spełniać
pewne równanie.
winny spełniać
pewne równanie.