3. Wykład III, 16.X.2009
Przykłady obliczeń odwzorowania Markowitza w najprostszych
sytuacjach – gdy okazuje się ono być liniowe lub kawałkami
liniowe. (Od takich prostych przykładów zaczyna się najczęściej,
bo rzadkie są sytuacje, gdy odchylenie standardowe portfela
Markowitza da się policzyć bez wyciągania pierwiastka kwadratowego.
Wykłady [13] też od tego zaczynały. Wielokąty wypukłe i odbicie
w pionowej osi ![]() , które czytelnik zobaczy
poniżej, pojawiały się już w [13]. Natomiast specyfiką
bieżących wykładów jest wielokrotne używanie w różnych
sytuacjach modeli
, które czytelnik zobaczy
poniżej, pojawiały się już w [13]. Natomiast specyfiką
bieżących wykładów jest wielokrotne używanie w różnych
sytuacjach modeli ![]() doskonale skorelowanych. Dokładniej,
szereg interesujących przykładów będzie się brał z odpowiedniego
zaburzania macierzy kowariancji postaci jak tu niżej
w I i II. Np przykład dany w przypisie nr 3
w Wykładzie XI (w wersji html jest to przypis nr 31) – do
macierzy
doskonale skorelowanych. Dokładniej,
szereg interesujących przykładów będzie się brał z odpowiedniego
zaburzania macierzy kowariancji postaci jak tu niżej
w I i II. Np przykład dany w przypisie nr 3
w Wykładzie XI (w wersji html jest to przypis nr 31) – do
macierzy ![]() doskonale skorelowanej dodana tam zostanie
macierz Id.)
doskonale skorelowanej dodana tam zostanie
macierz Id.)
I. Załóżmy przez chwilę, że zmienne losowe ![]() są
wszystkie doskonale dodatnio skorelowane, tzn
są
wszystkie doskonale dodatnio skorelowane, tzn ![]() dla
dla ![]() , albo też
, albo też ![]() dla
dla ![]() , tzn
, tzn ![]() .
Wtedy
.
Wtedy ![]() ,
, ![]() dla
dla ![]() .
.
Zatem ![]() dla
dla ![]() . Odwzorowanie Markowitza
jest w tym przypadku liniowe (dokładniej: zapisuje się
liniowymi wzorami; jego dziedzina
. Odwzorowanie Markowitza
jest w tym przypadku liniowe (dokładniej: zapisuje się
liniowymi wzorami; jego dziedzina ![]() rzecz prosta
nie jest przestrzenią liniową; nawet powłoka afiniczna
dziedziny, czyli hiperpłaszczyzna
rzecz prosta
nie jest przestrzenią liniową; nawet powłoka afiniczna
dziedziny, czyli hiperpłaszczyzna ![]() zdefiniowana w Wykładzie II
wzorem (2.2) , nie jest przestrzenią liniową).
zdefiniowana w Wykładzie II
wzorem (2.2) , nie jest przestrzenią liniową).
II. Zmienne losowe ![]() rozpadają się na dwie grupy
rozpadają się na dwie grupy
![]() oraz
oraz ![]() gdzie
gdzie ![]() .
Zakładamy, że zmienne w każdej z grup są parami doskonale dodatnio
skorelowane, zaś między grupami są doskonale ujemnie
skorelowane. Innymi słowy macierz współczynników korelacji to
.
Zakładamy, że zmienne w każdej z grup są parami doskonale dodatnio
skorelowane, zaś między grupami są doskonale ujemnie
skorelowane. Innymi słowy macierz współczynników korelacji to
![\Sigma\,\,=\,\left[\begin{array}[]{c}\sigma _{1}\\
\vdots\\
\sigma _{r}\\
-\sigma _{{r+1}}\\
\vdots\\
-\sigma _{k}\end{array}\right][\begin{array}[]{cccccc}\sigma _{1}&\dots&\sigma _{r}&-\,\sigma _{{r+1}}&\dots&-\,\sigma _{k}\end{array}]](wyklady/pk1/mi/mi366.png) |
Uwaga 3.1
Chociaż tak skrajne rozbicie spółek giełdowych na dwie antagonistyczne
grupy nigdy nie występuje w praktyce, to jednak coś trochę zbliżonego
obserwowano na giełdzie w Tokio bezpośrednio po katastrofalnym
trzęsieniu ziemi w mieście Kobe w styczniu 1995 roku. Wtedy korelacje
między stopami zwrotu z akcji firm budowlanych i ubezpieczeniowych były
między ![]() i
i ![]() , podczas gdy w warunkach stabilnych prawie
wszystkie współczynniki korelacji są między 0.5 i 0.7 .
(Średni współczynnik korelacji na NYSE wynosi 0.6 .)
, podczas gdy w warunkach stabilnych prawie
wszystkie współczynniki korelacji są między 0.5 i 0.7 .
(Średni współczynnik korelacji na NYSE wynosi 0.6 .)
W tej sytuacji ![]()
![x^{{\text{T}}}\left[\begin{array}[]{c}\sigma _{1}\\
\vdots\\
\sigma _{r}\\
-\sigma _{{r+1}}\\
\vdots\\
-\sigma _{k}\end{array}\right][\begin{array}[]{cccccc}\sigma _{1}&\dots&\sigma _{r}&-\,\sigma _{{r+1}}&\dots&-\,\sigma _{k}\end{array}]\, x\,=\,\left([\begin{array}[]{cccccc}\sigma _{1}&\dots&\sigma _{r}&-\,\sigma _{{r+1}}&\dots&-\,\sigma _{k}\end{array}]\, x\right)^{2}](wyklady/pk1/mi/mi317.png) |
oraz ![]()
dla ![]() . Zatem
. Zatem
Odwzorowanie Markowitza jest więc złożeniem liniowego przenoszącego
![]() na pewien wielokąt wypukły położony po obu stronach osi
na pewien wielokąt wypukły położony po obu stronach osi
![]() i ,,nakładki”
i ,,nakładki” ![]() ,
,
![]() .
.
Pierwsze z narzucających się tu pytań to
-
Czym są zbiory osiągalne
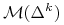 w sytuacjach
I i II?
w sytuacjach
I i II? -
Czym są granice: minimalna
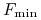 i maksymalna
i maksymalna 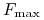 dla
dla 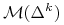 w sytuacjach I i II,
gdzie te granice definiowane są, i to ogólnie, nie tylko w sytuacjach
doskonałych, w sposób następujący
w sytuacjach I i II,
gdzie te granice definiowane są, i to ogólnie, nie tylko w sytuacjach
doskonałych, w sposób następujący
(Zbiory liniowe występujące w tych definicjach zawsze są ograniczone,
bo ![]() jest zbiorem zwartym w
jest zbiorem zwartym w ![]() .)
.)
Na temat zbiorów osiągalnych:
W sytuacji I
![\mathcal{M}(\Delta^{k})=\mathcal{M}\left(\text{conv}\left(\left(\begin{array}[]{c}1\\
0\\
\vdots\\
0\\
\end{array}\right),\left(\begin{array}[]{c}0\\
1\\
\vdots\\
0\\
\end{array}\right),\ldots,\left(\begin{array}[]{c}0\\
0\\
\vdots\\
1\end{array}\right)\right)\right)=\text{conv}\left(\mathcal{M}\left(\begin{array}[]{c}1\\
0\\
\vdots\\
0\\
\end{array}\right),\dots,\mathcal{M}\left(\begin{array}[]{c}0\\
0\\
\vdots\\
1\end{array}\right)\right)](wyklady/pk1/mi/mi373.png) |
![=\text{conv}\left\{\left(\begin{array}[]{c}\sigma _{i}\\
\mu _{i}\end{array}\right)\Bigg|\ i=1,\, 2,\dots,\, k\right\},](wyklady/pk1/mi/mi282.png) |
jest to więc ![]() -kąt wypukły,
-kąt wypukły, ![]() , położony w prawej (otwartej)
półpłaszczyźnie
, położony w prawej (otwartej)
półpłaszczyźnie ![]() , bo
, bo ![]() .
Dlaczego ogólnie
.
Dlaczego ogólnie ![]() -kąt, a nie po prostu
-kąt, a nie po prostu ![]() -kąt? Ponieważ niektóre (lub wiele
z nich) obrazy wierzchołków sympleksu
-kąt? Ponieważ niektóre (lub wiele
z nich) obrazy wierzchołków sympleksu ![]() mogą nie być punktami
ekstremalnymi tego zbioru wypukłego. Lub też, w sytuacji skrajnej, wszystkie
te obrazy mogą się pokrywać, dając w wyniku po prostu punkt (1-kąt wypukły).
mogą nie być punktami
ekstremalnymi tego zbioru wypukłego. Lub też, w sytuacji skrajnej, wszystkie
te obrazy mogą się pokrywać, dając w wyniku po prostu punkt (1-kąt wypukły).
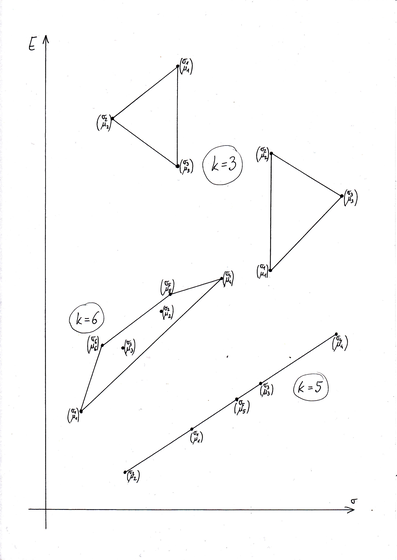
Niektóre z możliwych tu sytuacji są przedstawione na Rysunku 3.1 poniżej.
Natomiast w sytuacji II,
by uzyskać ![]() , najpierw tworzymy pomocniczy wielokąt wypukły
, najpierw tworzymy pomocniczy wielokąt wypukły![]() , który – uwaga – położony jest po obu stronach
osi
, który – uwaga – położony jest po obu stronach
osi ![]() . Dokładniej, chwilowo ignorujemy znak wartości bezwzględnej
w aktualnym wzorze na
. Dokładniej, chwilowo ignorujemy znak wartości bezwzględnej
w aktualnym wzorze na ![]() i stosujemy rachunek wypukły z sytuacji I.
Jedyna różnica w porównaniu do I jest taka, że teraz dostajemy jakiś
i stosujemy rachunek wypukły z sytuacji I.
Jedyna różnica w porównaniu do I jest taka, że teraz dostajemy jakiś ![]() -kąt
wypukły, gdzie
-kąt
wypukły, gdzie ![]() (nie dostajemy pojedynczego punktu, bo trafiamy w
obie półpłaszczyzny). Szukany
(nie dostajemy pojedynczego punktu, bo trafiamy w
obie półpłaszczyzny). Szukany ![]() jest obrazem tego
jest obrazem tego ![]() -kąta
przy przekształceniu
-kąta
przy przekształceniu ![]() ,
,
![]() ,
które zachowuje punkty w prawej półpłaszczyźnie, zaś punkty z lewej
półpłaszczyzny odbija w pionowym lustrze do prawej.
,
które zachowuje punkty w prawej półpłaszczyźnie, zaś punkty z lewej
półpłaszczyzny odbija w pionowym lustrze do prawej.
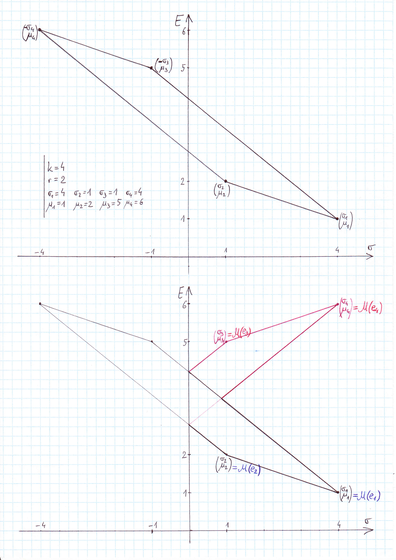
Przykład 3.1
Weźmy ![]() ,
, ![]() oraz
oraz ![]() . Na Rysunku 3.2 tuż poniżej pokazane
jest powstawanie zbioru
. Na Rysunku 3.2 tuż poniżej pokazane
jest powstawanie zbioru ![]() we wspomnianych dwóch krokach;
we wspomnianych dwóch krokach; ![]() ,
,
![]() ,
, ![]() ,
, ![]() to, oczywiście, kolejne wierzchołki sympleksu
to, oczywiście, kolejne wierzchołki sympleksu ![]() .
.
Na temat granic minimalnych i maksymalnych:
Te pytania w sytuacji I są całkiem elementarne, nietrudno scharakteryzować (i należy to zrobić samemu!) rodziny łamanych, którymi są takie granice.
Jednak już w sytuacji II, nawet przy ustalonym dyskretnym parametrze
![]() , opisy granic stają się dosyć skomplikowane.
Zatrzymajmy się na chwilę przy tych opisach.
, opisy granic stają się dosyć skomplikowane.
Zatrzymajmy się na chwilę przy tych opisach.
![]() jest wtedy łamaną o nie więcej niż
jest wtedy łamaną o nie więcej niż ![]() bokach, przy czym ta ilość
jest osiągana przy każdym
bokach, przy czym ta ilość
jest osiągana przy każdym ![]() i każdym
i każdym ![]() (dlaczego?).
(dlaczego?). ![]() jest więc najmniejszym
ograniczeniem górnym ilości boków łamanej
jest więc najmniejszym
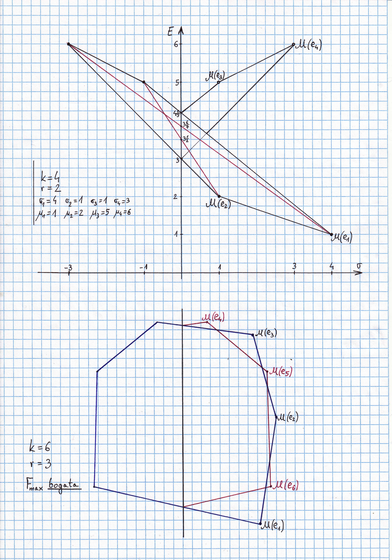
ograniczeniem górnym ilości boków łamanej ![]() . Np na Rysunku 3.2, przy
. Np na Rysunku 3.2, przy ![]() i
i ![]() , łamana
, łamana ![]() składa się z 5 boków. Tak samo jest w sytuacji przedstawionej
w górnej części Rysunku 3.3 tuż poniżej, choć ten przykład jest subtelniejszy od
poprzedniego i będzie w przyszłości wykorzystany w innym celu.
składa się z 5 boków. Tak samo jest w sytuacji przedstawionej
w górnej części Rysunku 3.3 tuż poniżej, choć ten przykład jest subtelniejszy od
poprzedniego i będzie w przyszłości wykorzystany w innym celu.
Ćwiczenie 3.1
W sytuacji ![]() doskonale skorelowanej przy ustalonych wielkościach
doskonale skorelowanej przy ustalonych wielkościach ![]() i
i ![]() ,
znaleźć najmniejsze ograniczenie górne (dlaczego takie istnieje?) ilości boków
łamanej
,
znaleźć najmniejsze ograniczenie górne (dlaczego takie istnieje?) ilości boków
łamanej ![]() .
.
Zanalizować przykład pokazany w dolnej części Rysunku 3.3 powyżej, gdzie
przy ![]() i
i ![]() granica (tu łamana) maksymalna składa się z 10 boków.
granica (tu łamana) maksymalna składa się z 10 boków.
Pokazać, że poszukiwanym ograniczeniem jest funkcja od ![]() i
i ![]() zdefiniowana
następująco
zdefiniowana
następująco
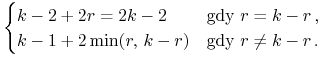 |
(To zadanie rozwiązują, z różnymi efektami, kolejne roczniki słuchaczy wykładów
z APRK1 na Wydziale MIM. Stanowi ono dobry wstęp do poznania i rozumienia ,,parasolkowatej”
natury granicy maksymalnej ![]() dla ogólnych odwzorowań Markowitza
– gdy odrzuci się sztuczne założenie
dla ogólnych odwzorowań Markowitza
– gdy odrzuci się sztuczne założenie ![]() doskonałej korelacji zmiennych stóp
zwrotu.)
doskonałej korelacji zmiennych stóp
zwrotu.)
Dygresja nt podprzestrzeni zerowych form kwadratowych nieujemnie określonych.
Chodzi tu o zbiory wektorów, na których zerują się formy kwadratowe nieujemnie
określone. Często, ustalając bazę w przestrzeni ![]() (np bazę standardową
(np bazę standardową
![]() ), utożsamia się formy z macierzami nieujemnie określonymi
), utożsamia się formy z macierzami nieujemnie określonymi
![]() . Zaczynamy od prostego pytania
. Zaczynamy od prostego pytania
Ćwiczenie 3.2
Czy macierze ![]() w sytuacjach doskonale skorelowanych
I i II są dodatnio określone ?
w sytuacjach doskonale skorelowanych
I i II są dodatnio określone ?
Nie, gdyż mają one duże zbiory wektorów ![]() zerujących
odpowiadającą im formę kwadratową
zerujących
odpowiadającą im formę kwadratową ![]() . Z wcześniejszych obliczeń
wiemy, że te zbiory są hiperpłaszczyznami liniowymi:
. Z wcześniejszych obliczeń
wiemy, że te zbiory są hiperpłaszczyznami liniowymi: ![]() w sytuacji I, względnie
w sytuacji I, względnie ![]() w sytuacji II.
w sytuacji II.
Trochę trudniej jest pokazać, że
Ćwiczenie 3.3
![]() jest podprzestrzenią liniową
jest podprzestrzenią liniową ![]() . Jest to właśnie tzw.
podprzestrzeń zerowa formy mającej macierz
. Jest to właśnie tzw.
podprzestrzeń zerowa formy mającej macierz ![]() .
.
![]() oraz też
oraz też ![]() . Te dwie nierówności dają łącznie
. Te dwie nierówności dają łącznie ![]() , i dalej
, i dalej ![]() .
.
Dokładniejszą informację może dać
Ćwiczenie 3.4
Ustalić (jeśli istnieje) związek między rzędem macierzy ![]() i wymiarem jej podprzestrzeni zerowej.
i wymiarem jej podprzestrzeni zerowej.
Zauważmy jeszcze, tylko informacyjnie, że ogólnie zbiór wektorów zerujących daną formę kwadratową nie musi mieć struktury przestrzeni liniowej.
Przykład 3.2
Już forma kwadratowa na ![]() mająca w bazie standardowej macierz
mająca w bazie standardowej macierz
![]() ,
tj przyjmująca na wektorze
,
tj przyjmująca na wektorze ![]() wartość
wartość
![]() , jest taka.
, jest taka.
Gdy macierz kowariancji ![]() jest dodatnio określona, wtedy (oczywiście)
żaden portfel Markowitza nie ma zerowego ryzyka. Natomiast czasami, i to już
przy
jest dodatnio określona, wtedy (oczywiście)
żaden portfel Markowitza nie ma zerowego ryzyka. Natomiast czasami, i to już
przy ![]() , można zmniejszać ryzyko portfela Markowitza poniżej wielkości
, można zmniejszać ryzyko portfela Markowitza poniżej wielkości
![]() . Tak jest w obu przykładach w Wykładzie I;
porównaj w szczególności Rysunek 1.2 dotyczący jednego z nich. Czasami zaś
nie można zejść poniżej
. Tak jest w obu przykładach w Wykładzie I;
porównaj w szczególności Rysunek 1.2 dotyczący jednego z nich. Czasami zaś
nie można zejść poniżej ![]() , jak w przykładzie
,,5 stanów giełdy” w Wykładzie II, porównaj z kolei Rysunek 2.1. Od czego
to zatem zależy? Przynajmniej przy
, jak w przykładzie
,,5 stanów giełdy” w Wykładzie II, porównaj z kolei Rysunek 2.1. Od czego
to zatem zależy? Przynajmniej przy ![]() chcielibyśmy mieć tu jasność.
chcielibyśmy mieć tu jasność.
Pełny opis zbioru![]() .
.
Język naszego opisu to ![]() .
Liczby
.
Liczby ![]() są rzeczywiste nie mniejsze niż
są rzeczywiste nie mniejsze niż ![]() i różne, by
portfele mogły mieć różne wartości oczekiwane. Liczy
i różne, by
portfele mogły mieć różne wartości oczekiwane. Liczy ![]() są dodatnie,
natomiast
są dodatnie,
natomiast ![]() . Podczas rachunku przyjmujemy domyślnie,
że jeśli
. Podczas rachunku przyjmujemy domyślnie,
że jeśli ![]() , to wtedy
, to wtedy ![]() .
.
Celem jest, czego domyślamy się już z dotychczasowych doświadczeń
i na wykładzie i na ćwiczeniach, uzyskanie hiperboli na płaszczyźnie
![]() , względnie paraboli na płaszczyźnie
, względnie paraboli na płaszczyźnie ![]() (parabola będzie nawet wtedy, kiedy hiperbola przy
(parabola będzie nawet wtedy, kiedy hiperbola przy ![]() zdegeneruje
się do pary prostych).
zdegeneruje
się do pary prostych).
Obliczamy wariancję portfela, parametryzując najpierw parametrem ![]() :
:
| (3.1) |
podczas gdy
albo
| (3.2) |
i to wyrażenie będzie można podstawić do (3.1).
Uwaga 3.2
Jest jeden jedyny przypadek, gdy (3.1) nie wyraża
kwadratowej zależności ![]() od
od ![]() :
: ![]() i
i ![]() . Wtedy znikają tam współczynniki przy
. Wtedy znikają tam współczynniki przy ![]() oraz
oraz ![]() ,
i przez to
,
i przez to ![]() . Ten przypadek wykluczyliśmy na początku rachunku.
. Ten przypadek wykluczyliśmy na początku rachunku.
Trójmian wyrażający wariancję ma minimum w
z czego wyliczamy, dzięki (3.2), wartość oczekiwaną ![]() odpowiadającą tej wartości
odpowiadającą tej wartości ![]() ,
,
| (3.3) |
Patrząc teraz równocześnie na (3.1) i (3.2), widzimy, że szukana hiperbola musi mieć równanie postaci
przy czym w analizie portfelowej ciekawa jest tylko gałąź ![]() .
.
Trochę dodatkowych rachunków pozwala wyznaczyć wartość stałej po prawej
stronie,
| (3.4) |
Gdy ![]() (więc
(więc ![]() gdy
gdy ![]() ),
w (3.4) mamy dwie proste krzyżujące się w
),
w (3.4) mamy dwie proste krzyżujące się w
![]() .
.
Gdy ![]() , w (3.4) mamy hiperbolę w płaszczyźnie
, w (3.4) mamy hiperbolę w płaszczyźnie
![]() , z półosiami długości
, z półosiami długości
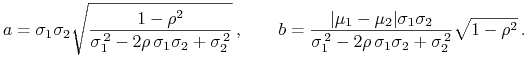 |
(3.5) |
W każdym z tych przypadków obrazy portfeli Markowitza (które nas chwilowo
jedynie interesują) to części wymienionych krzywych leżące w półpłaszczyźnie
![]() i w poziomym pasie położonym między
i w poziomym pasie położonym między ![]() oraz
oraz ![]() .
.
Skrajne wartości![]() , gdy uzmienniamy parametr
, gdy uzmienniamy parametr![]() .
.
Podstawiamy teraz w (3.3) ![]() :
:
![]() jest więc punktem podziału zewnętrznego odcinka
o końcach
jest więc punktem podziału zewnętrznego odcinka
o końcach ![]() ,
, ![]() w stosunku
w stosunku ![]() (i nie
istnieje, gdy
(i nie
istnieje, gdy ![]() , lecz ten przypadek od początku
wykluczyliśmy).
, lecz ten przypadek od początku
wykluczyliśmy).
Obserwacja. 3.1.
Gdy ![]() rośnie od
rośnie od ![]() do
do ![]() , wtedy
, wtedy ![]() dane wzorem (3.3)
zmienia się ściśle monotonicznie.
dane wzorem (3.3)
zmienia się ściśle monotonicznie.
Prawa strona w (3.3) to funkcja homograficzna od ![]() . Zapisujemy
ją inaczej, jak (być może) robiliśmy to już kiedyś na zajęciach z Funkcji
Analitycznych:
. Zapisujemy
ją inaczej, jak (być może) robiliśmy to już kiedyś na zajęciach z Funkcji
Analitycznych:
| (3.6) |
Ścisła monotoniczność ![]() jest już teraz widoczna.
jest już teraz widoczna.
Np w sytuacji na rysunku poniżej, mimo braku numeracji obrazów wierzchołków,
musi być albo ![]() i
i ![]() , albo też
, albo też ![]() i
i ![]() , więc licznik ułamka w (3.6) przy
każdej z tych możliwych numeracji jest ujemny i
, więc licznik ułamka w (3.6) przy
każdej z tych możliwych numeracji jest ujemny i ![]() ściśle maleje od
ściśle maleje od ![]() do
do ![]() [w wersji pdf Rysunek 3.4 przeskoczył
na następną stronę].
[w wersji pdf Rysunek 3.4 przeskoczył
na następną stronę].
Obserwacja. 3.2.
Gdy ![]() ,
, ![]() i
i ![]() rośnie od
rośnie od ![]() do
do ![]() ,
wtedy rozwartość kąta między asymptotami hiperboli (3.4) ściśle
rośnie od
,
wtedy rozwartość kąta między asymptotami hiperboli (3.4) ściśle
rośnie od ![]() do
do
![]() .
.
Według (3.5), ![]() .
.
Krytyczna wartość współczynnika korelacji.
Postawmy sobie pozornie uboczne pytanie, kiedy (tj dla jakiej
wartości ![]() )
) ![]() , tzn. kiedy
, tzn. kiedy ![]() jest czubkiem gałęzi hiperboli (3.4). Według (3.3),
jest czubkiem gałęzi hiperboli (3.4). Według (3.3),
tzn.
tzn. ![]() , przy czym równość
, przy czym równość ![]() jest tutaj wykluczona, bo oznaczałaby (dodatkowo)
jest tutaj wykluczona, bo oznaczałaby (dodatkowo) ![]() .
.
Rozumując symetrycznie, ![]() pociąga za sobą,
że
pociąga za sobą,
że ![]() .
.
Wniosek 3.1
Czubek gałęzi hiperboli (3.4) pokrywa się z jednym
z obrazów wierzchołków ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
Krytyczna wartość współczynnika korelacji, zdefiniowana powyższym wzorem, to bardzo ważne narzędzie w analizie portfelowej. Bywa ono pomocne w zupełnie niespodziewanych sytuacjach, także w przykładach i zadaniach z ilością spółek większą niż dwa (o czym studenci często nie pamiętają).
Ćwiczenie 3.5
Policzyć wartość ![]() w przykładzie na Rysunku 3.4 powyżej.
w przykładzie na Rysunku 3.4 powyżej.
Przykład 3.3
W przykładzie ,,5 stanów giełdy” z Wykładu II wartość współczynnika
korelacji ![]() jest właśnie krytyczna:
jest właśnie krytyczna:
Ten efekt krytyczności ![]() widać wyraźnie na
Rysunku 2.1 w Wykładzie II: czubek gałęzi hiperboli jest tam
na wysokości 0.05 .
widać wyraźnie na
Rysunku 2.1 w Wykładzie II: czubek gałęzi hiperboli jest tam
na wysokości 0.05 .
Definicja 3.1
Wartości ![]() nazywamy
podkrytycznymi, natomiast wartości
nazywamy
podkrytycznymi, natomiast wartości ![]() nazywamy nadkrytycznymi.
nazywamy nadkrytycznymi.
W obu przykładach w Wykładzie I wartości współczynników korelacji są podkrytyczne: w pierwszym można to sprawdzić bezpośrednim rachunkiem, zaś w drugim kowariancja między stopami zwrotu jest ujemna.
Nasuwa się pytanie, które łuki hiperbol na Rysunku 3.4 powyżej
odpowiadają nadkrytycznym wartościom ![]() ?
?