6. Wykład VI, 6.XI.2009.

W Wykładzie V przerwaliśmy dyskusję strategii inwestora, który na początku okresu inwestycyjnego zajął zarówno długie jak i krótkie pozycje (te ostatnie – korzystając z ,,nieograniczonej uprzejmości Domu Maklerskiego” – modelowanie Blacka jest bardzo poręczną, lecz tylko idealizacją). Wiemy, co zrobił on na początku okresu inwestycyjnego. Co teraz zrobi na końcu tego okresu?

Otóż akcje, w których zajął długie pozycje (o numerach, jak pamiętamy, $i\in I$ ) inwestor będzie trzymał do końca okresu inwestycyjnego, kiedy to sprzeda je na giełdzie po cenie $C_{{i,\,\text{kon}}}$ . Natomiast akcje, w których zajął krótkie pozycje (o numerach $j\in J$ ) miał tylko pożyczone od DM i od razu je sprzedał. Na końcu okresu będzie je odkupował po cenie $C_{{j,\,\text{kon}}}$ by zwrócić je do DM. Zwroty inwestora w jednym i drugim przypadku będą liczone inaczej! Za chwilę uwzględnimy to przy obliczaniu łącznej stopy zwrotu inwestora; ujemne składniki portfela $x_{j}<0$ okażą się dobrze pasować do całości rachunku.

Wcześniej przyjrzyjmy się jeszcze jednemu, bardziej rozbudowanemu niż w prostym Ćwiczeniu 5.4 w Wykładzie V, przykładowi portfela inwestora przy nieograniczonej krótkiej sprzedaży à la Black (zaczerpniętemu z [4]).

Przykład 6.1

Przykład portfela akcji 10 spółek silnie używającego krótkiej sprzedaży:

Walor nr	Udział w portfelu w procentach
1	$647.1$
2	$770.6$
3	$729.4$
4	$1741.2$
5	$211.6$
6	$-152.9$
7	$-447.1$
8	$-594.1$
9	$-741.2$
10	$-2070.6$

Udziały sumują się do 100 $\%$ (do 100 $\%$ kapitału własnego inwestora, w stosunku do którego wszystko jest tu podawane, czy kodowane).

Uwaga 6.1

Zwracamy uwagę, że na tej samej stronie w [4] wspominana jest też zupełnie inna krótka sprzedaż, zdefiniowana czy modelowana przez Lintnera w pracy [16]. Jest ona przeciwieństwem podejścia Blacka i współautorów – jest bardzo mocno ograniczona. Poznamy ją dokładnie na Wykładzie IX.

Jeszcze dwa zdania na temat tych trochę tajemniczych `współautorów' wybitnego ekonomisty Blacka⁸lecz, niestety, z losowych powodów nie laureata nagrody Nobla z ekonomii, cytując z [22], strona 39: ,,I refer to the model whose only constraint is $\sum _{i}X_{i}=1$ as Black's model, for ease of reference and because the results of [3] are frequently cited in connection with this model. It would probably be more accurate to name it Roy-Sharpe-Merton-Black, but that is a lot of name for a simple, frequently cited model.”

Zadajmy sobie teraz pytanie, czy podstawowy paradygmat Markowitza,

$\Delta^{k}\ni x\longleftrightarrow x^{{\text{T}}}R=x_{1}R_{1}+\cdots+x_{k}R_{k}$

dający klasyczny wzór na stopę zwrotu (zmienną losową!) z portfela Markowitza (Wykład II) rozszerza się na wszystkie portfele Blacka $\{ x\in H\}$ ?

By odpowiedzieć na to pytanie, trzymamy się oznaczeń z Wykładu V, gdzie ujemne składniki portfela $x$ miały indeksy $j\in J$ , dodatnie miały indeksy $i\in I,\ I,\, J\subset\{ 1,\, 2,\dots,\, k\}$ , przy czym oczywiście $I\cap J=\emptyset$ , zaś $L$ był kapitałem własnym inwestora. Stopę zwrotu (cały czas zmienną losową) liczymy teraz dużo staranniej niż w Wykładzie II.

		$\displaystyle\text{stopa zwrotu inwestora mającego portfel }x\,=\,\frac{\text{przychody}-\text{rozchody przy takim portfelu }x}{L}$
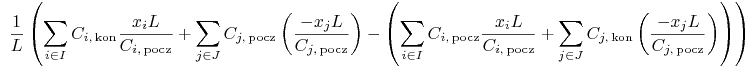	$\displaystyle=$	$\displaystyle\,\,\frac{1}{L}\left(\sum _{{i\in I}}C_{{i,\,\text{kon}}}\frac{x_{i}L}{C_{{i,\,\text{pocz}}}}+\sum _{{j\in J}}C_{{j,\,\text{pocz}}}\left(\frac{-x_{j}L}{C_{{j,\,\text{pocz}}}}\right)-\left(\sum _{{i\in I}}C_{{i,\,\text{pocz}}}\frac{x_{i}L}{C_{{i,\,\text{pocz}}}}+\sum _{{j\in J}}C_{{j,\,\text{kon}}}\left(\frac{-x_{j}L}{C_{{j,\,\text{pocz}}}}\right)\right)\right)$
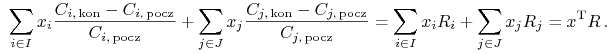	$\displaystyle=$	$\displaystyle\,\,\sum _{{i\in I}}x_{i}\frac{C_{{i,\,\text{kon}}}-C_{{i,\,\text{pocz}}}}{C_{{i,\,\text{pocz}}}}+\sum _{{j\in J}}x_{j}\frac{C_{{j,\,\text{kon}}}-C_{{j,\,\text{pocz}}}}{C_{{j,\,\text{pocz}}}}=\sum _{{i\in I}}x_{i}R_{i}+\sum _{{j\in J}}x_{j}R_{j}=x^{{\text{T}}}R\,.$

(Czytelnik zwróci w tym rachunku uwagę na specyficzny sposób obliczania zysku z akcji krótko sprzedanych: od ceny początkowej $C_{{j,\,\text{pocz}}}$ odejmuje się cenę końcową $C_{{j,\,\text{kon}}}$ . Istotnie, powtarzając się nawet, bo to kluczowe przy modelowaniu Blacka: ta pierwsza jest ceną sprzedaży akcji o numerze $j$ , zaś ta druga jest ich ceną zakupu, tzn. ceną, po której inwestor odkupuje akcje o numerze $j$ , by zwrócić je Domowi Maklerskiemu. Porównaj też strony 11 i 39 w książce [22]; fragmentem z tej drugiej wymienionej strony rozpoczęliśmy bieżący Wykład VI.)

Podsumujmy zatem: tak, paradygmat Markowitza, czyli klasyczny wzór na stopę zwrotu z portfela, obowiązuje także w modelu Blacka!

Wniosek 6.1

Wzory na wariancję portfela $\sigma^{2}(x)\,\left(=\sigma^{2}(x^{{\text{T}}}R)\right)$ oraz na wartość oczekiwaną $E(x)\,\left(=\mathbb{E}(x^{{\text{T}}}R)\right)$ pozostają w mocy dla wszystkich $x\in H$ i dlatego właśnie ważne są odwzorowania Markowitza $\mathcal{M}$ i $\widetilde{\mathcal{M}}$ idące z całej hiperpłaszczyzny $H$ . Badając te odwzorowania już od pewnego czasu, antycypowaliśmy zgodność, o której tu mowa.

Uwaga 6.2

Dopuszczenie nieograniczonej krótkiej sprzedaży wywołuje jedną fundamentalną zmianę w porównaniu z podejściem Markowitza. Od pierwszych wykładów było jasne, że wszystkie wartości oczekiwane $\mu _{i}=\mathbb{E}(R_{i})$ są niemniejsze niż $-1$ , gdyż zmienne losowe $R_{i}$ przyjmują tylko takie wartości. To prowadziło do naturalnych ograniczeń na wartości oczekiwane zmiennych Markowitza $x^{{\text{T}}}R$ , $x\in\Delta^{k}$ , gdyż były one, oczywiście, $x$ -kombinacjami wypukłymi liczb $\mu _{1},\dots,\,\mu _{k}$ .

Tymczasem zmienne Blacka $x^{{\text{T}}}R$ , $x\in H$ , mają wartości oczekiwane będące $x$ -kombinacjami afinicznymi liczb $\mu _{1},\dots,\,\mu _{k}$ , które (o ile tylko nie wszystkie $\mu _{i}$ są sobie równe) nie są poddane żadnym ograniczeniom i ,,biegają” po całej osi liczbowej. Koniec wtedy z ograniczeniem $-1$ z dołu; nieograniczona krótka sprzedaż znosi to ograniczenie! Przychody minus rozchody inwestora mogą być w podejściu Blacka dowolnie wielkie ujemne w stosunku do jego kapitału własnego $L$ . (Mogą też oczywiście być dowolnie wielkie dodatnie – co często podkreśla się w literaturze, lecz i ujemne też! W modelu Blacka inwestor może np stracić na giełdzie w okresie inwestycyjnym, średnio biorąc, tysiąckrotność kapitału własnego.) To jest prawdziwa pojęciowa rewolucja, z której słabo zdajemy sobie sprawę, gdy pierwszy raz oglądamy definicję nieograniczonej krótkiej sprzedaży.

By nie być tu gołosłownym, w Przykładzie 5.1 (w Wykładzie V; jest on kontynuowany jako Przykład 6.3 tu niżej) mieliśmy sytuację, gdzie wszystkie wartości oczekiwane $\mu _{i}$ były niemniejsze niż $-1$ . Mimo to, gdy traktujemy go rozszerzająco jako model Blacka (tak właśnie jest w Przykładzie 6.3), wtedy pewna istotna wielkość $E_{0}$ uogólniająca $E_{0}(\rho)$ ze wzoru (3.3) z Wykładu III okazuje się dużo mniejsza niż $-1$ : $E_{0}=-\frac{19}{12}$ . Już to pokazuje, że modelowanie Blacka łatwo zaczyna żyć własnym życiem i łatwo wymyka się spod kontroli . . .

Pamiętajmy zatem, że Black to cała hiperpłaszczyzna $H$ wraz z całym tego dobrodziejstwem inwentarza – m. in. nieograniczonymi z obu stron wartościami oczekiwanymi portfeli Blacka.

Jednakże, dopuszczając nieograniczoną krótką sprzedaż akcji, bardzo znacznie zyskujemy na łatwości operowania modelem, jak też na ogólności i elegancji opisu. Trochę doświadczenia dało nam już domykanie Rysunku 4.6 w Wykładzie IV (w szczególności piękny Rysunek 4.7 tamże). Ważne były tam obrazy prostych krytycznych; bez nich rysunki były mocno niekompletne i trudne do interpretacji.

Jednak tamte proste krytyczne cięły sympleks standardowy, a tak przecież być nie musi.

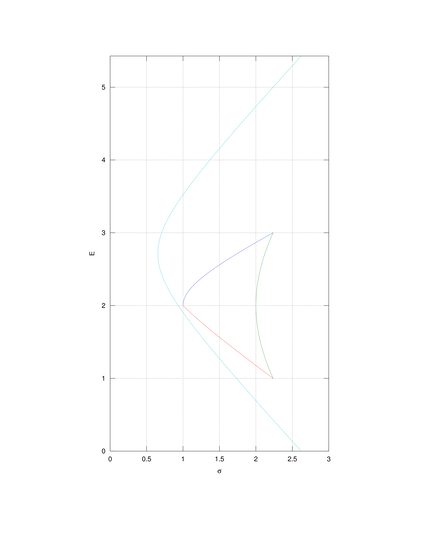
Dla przeciwwagi chcemy teraz pokazać obraz przy odwzorowaniu $\mathcal{M}$ (a więc tym razem na płaszczyźnie $\mathbb{R}^{2}(\sigma,\, E)$ ) zbiorów osiągalnych w obu aspektach, Markowitza i Blacka, $\mathcal{M}(\Delta^{3})\subset\mathcal{M}(H)$ , gdy prosta krytyczna omija sympleks. (Parametry tego przykładu pochodzą z pewnego kolokwium z APRK1 na Wydziale MIM UW.)

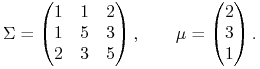$\Sigma=\begin{pmatrix}1&1&2\\ 1&5&3\\ 2&3&5\end{pmatrix},\qquad\mu=\begin{pmatrix}2\\ 3\\ 1\end{pmatrix}.$

(6.1)

[W wersji pdf rysunek trafił na następną stronę.]

$\par$

Rys. 6.1. Markowitz całkowicie zdominowany przez Blacka: obraz sympleksu we wnętrzu obrazu płaszczyzny.

Jest to co prawda tylko jeden kamyk z ogromnej mozaiki. Proponujemy tu jednak czytelnikowi całą serię pytań sprawdzających.

Ćwiczenie 6.1

1. Patrząc na sam Rysunek 6.1, jaką dokładnie wartość ma współczynnik korelacji $\rho _{{12}}$ ? Co można powiedzieć o wartości $\rho _{{13}}$ ?

2. Dla danych (6.1) znaleźć zbiór portfeli krytycznych Blacka (np używając w tym celu Twierdzenia 5.1 z Wykładu V). Czym jest ten zbiór i jak jest on położony względem sympleksu standardowego $\Delta^{3}$ ?

3. Czy poprzednie pytanie pomaga w ,,rozszyfrowaniu” całego Rysunku 6.1 ? Czy zbiór krytyczny okazuje się do tego pomocny? Czy jego nazwa współgra z rolą, jaką on odgrywa?

4. Granica minimalna w aspekcie Markowitza (patrz definicja $F_{{\min}}$ w Wykładzie III) ma bardzo wyraźny punkt załamania (kink) na wysokości $E=2$ . Ten punkt załamania to obraz wierzchołka $e_{1}$ , który tutaj leży – porównaj punkt 2 – poza zbiorem krytycznym. Dokładniej, przekształcenie Markowitza $\mathcal{M}$ jest tutaj w otoczeniu $e_{1}$ dyfeomorfizmem. Czy czytelnik widzi związek tego faktu z pojawieniem się kinka?

5. Czy są w płaszczyźnie $H$ portfele Blacka nie będące Markowitza, które w mapie ryzyko – wartość oczekiwana też trafiają w zbiór $\mathcal{M}(\Delta^{3})$ ? Gdzie leżą (albo: gdzie powinny leżeć) te ,,fałszywe portfele Markowitza”?

Po serii doświadczeń i ćwiczeń (w poprzednim Wykładzie V i bieżącym VI) upewniliśmy się już, że kluczową rolę w badaniu własności odwzorowań $\mathcal{M}$ i $\widetilde{\mathcal{M}}$ odgrywają portfele krytyczne Blacka. Zbiór wszystkich portfeli krytycznych nie zawsze jest prostą (o czym już słyszeliśmy w tych wykładach). Utrwalmy to jeszcze.

Przykład 6.2 (kontynuacja Rysunku 3.2)

Znajdźmy wszystkie portfele krytyczne w tamtym modelu Blacka.
Według Twierdzenia 5.1 (Wykład V) szukamy portfeli $x\in H$ takich, że $\text{rk}\big(\Sigma x,\,\mu,\, e\big)=2$ , tzn.

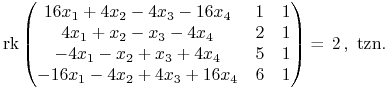$\text{rk}\begin{pmatrix}16x_{1}+4x_{2}-4x_{3}-16x_{4}&1&1\\ 4x_{1}+x_{2}-x_{3}-4x_{4}&2&1\\ -4x_{1}-x_{2}+x_{3}+4x_{4}&5&1\\ -16x_{1}-4x_{2}+4x_{3}+16x_{4}&6&1\end{pmatrix}=\, 2\,,\,\,\text{tzn.}$

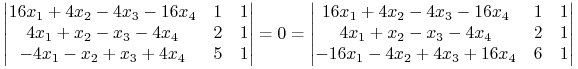$\begin{vmatrix}16x_{1}+4x_{2}-4x_{3}-16x_{4}&1&1\\ 4x_{1}+x_{2}-x_{3}-4x_{4}&2&1\\ -4x_{1}-x_{2}+x_{3}+4x_{4}&5&1\end{vmatrix}=0=\begin{vmatrix}16x_{1}+4x_{2}-4x_{3}-16x_{4}&1&1\\ 4x_{1}+x_{2}-x_{3}-4x_{4}&2&1\\ -16x_{1}-4x_{2}+4x_{3}+16x_{4}&6&1\end{vmatrix}$

(opuszczone zostały, odpowiednio, czwarty i trzeci wiersz w macierzy $4\times 3$ ). Po rozwinięciu tych wyznaczników dostajemy

$-28x_{1}-7x_{2}+7x_{3}+28x_{4}\,=\, 0\,=\,-28x_{1}-7x_{2}+7x_{3}+28x_{4}\,,$

a więc (dwa razy) jedno i to samo równanie, nie zaś dwa różne równania! Zresztą równanie tożsame z opisem portfeli zerowego ryzyka.⁹Ćwiczenie 5.2 w Wykładzie V było na bardzo podobny temat. Tutaj w Przykładzie 6.2 nie występuje specjalna konfiguracja geometryczna, która tam stanowiła swoisty haczyk. Tak więc zbiór portfeli krytycznych pokrywa się tutaj ze zbiorem portfeli zerowego ryzyka i jest 2-wymiarową płaszczyzną.

Ćwiczenie 6.2

Jak płaszczyzna krytyczna w tym przypadku położona jest względem sympleksu $\Delta^{4}$ ? (Tzn. które portfele Markowitza są krytyczne?)

Wskazówka:

Przyglądając się równaniu tej płaszczyzny (po skróceniu poprzednio otrzymanego równania stronami przez $-7$ ) $4x_{1}+x_{2}-x_{3}-4x_{4}=0$ , na pewnych czterech z sześciu krawędzi (na których?) sympleksu $\Delta^{4}$ bez trudu znajdujemy cztery specjalne punkty przecięcia płaszczyzny z sympleksem. Ich powłoka wypukła (czworokąt wypukły z wnętrzem) jest całym przecięciem płaszczyzny krytycznej z $\Delta^{4}$ . Jeśli chodzi o przedział wartości oczekiwanych $E$ portfeli krytycznych Markowitza, to można go w przybliżeniu doświadczalnie odczytać (bądź domyślić się) z Rysunku 3.2 w Wykładzie III, dokładnie zaś obliczyć – po przyjrzeniu się wspomnianemu wyżej czworokątowi.

Do tej analizy położeń wrócimy w przyszłości, poszukując przykładów niejednoznacznych tzw. łamanych wierzchołkowych w aspekcie Markowitza (patrz Wykłady X i XI).

Zauważmy też, że w Przykładzie 6.2 macierz $\Sigma$ była silnie zdegenerowana, $\text{rk}\,\Sigma=1$ (wobec maksymalnej możliwej wartości 4). Zatrzymajmy się na chwilę nad tym zjawiskiem.

Ćwiczenie 6.3 (sprawdzające)

Obliczyć $\text{rk}\,\Sigma$ w każdej sytuacji doskonale skorelowanej i w każdej sytuacji $\pm$ doskonale skorelowanej.

Rozwiązanie:

W sytuacji doskonałej dodatniej korelacji macierz $\Sigma$ jest postaci

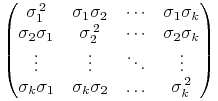$\begin{pmatrix}\sigma _{1}^{{\, 2}}&\sigma _{1}\sigma _{2}&\cdots&\sigma _{1}\sigma _{k}\\ \sigma _{2}\sigma _{1}&\sigma _{2}^{{\, 2}}&\cdots&\sigma _{2}\sigma _{k}\\ \vdots&\vdots&\ddots&\vdots\\ \sigma _{k}\sigma _{1}&\sigma _{k}\sigma _{2}&\dots&\sigma _{k}^{{\, 2}}\end{pmatrix}$

i łatwo widać, iż jej $i$ -ty wiersz jest postaci $\sigma _{i}\cdot(\sigma _{1},\,\sigma _{2},\dots,\,\sigma _{k})$ . Wszystkie jej wiersze są liniowo zależne i nie jest ona zerowa, zatem jej rząd wynosi 1.

W sytuacji $\pm$ doskonałej korelacji macierz $\Sigma$ jest postaci

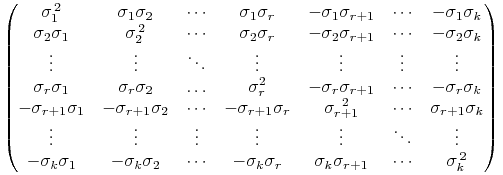$\begin{pmatrix}\sigma _{1}^{{\, 2}}&\sigma _{1}\sigma _{2}&\cdots&\sigma _{1}\sigma _{r}&-\sigma _{1}\sigma _{{r+1}}&\cdots&-\sigma _{1}\sigma _{k}\\ \sigma _{2}\sigma _{1}&\sigma _{2}^{{\, 2}}&\cdots&\sigma _{2}\sigma _{r}&-\sigma _{2}\sigma _{{r+1}}&\cdots&-\sigma _{2}\sigma _{k}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots\\ \sigma _{r}\sigma _{1}&\sigma _{r}\sigma _{2}&\dots&\sigma _{r}^{2}&-\sigma _{r}\sigma _{{r+1}}&\cdots&-\sigma _{r}\sigma _{k}\\ -\sigma _{{r+1}}\sigma _{1}&-\sigma _{{r+1}}\sigma _{2}&\cdots&-\sigma _{{r+1}}\sigma _{r}&\sigma _{{r+1}}^{{\,\,\, 2}}&\cdots&\sigma _{{r+1}}\sigma _{k}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ -\sigma _{k}\sigma _{1}&-\sigma _{k}\sigma _{2}&\cdots&-\sigma _{k}\sigma _{r}&\sigma _{k}\sigma _{{r+1}}&\cdots&\sigma _{k}^{{\, 2}}\end{pmatrix}$

i łatwo widać, iż jej $i$ -ty wiersz jest postaci $\sigma _{i}\cdot(\sigma _{1},\,\sigma _{2},\dots,\,\sigma _{r},-\sigma _{{r+1}},\dots,-\sigma _{k})$ , gdy $i\in\{ 1,\, 2,\dots,\, r\}$ , zaś jej $j$ -ty wiersz jest postaci $-\sigma _{j}\cdot(\sigma _{1},\,\sigma _{2},\dots,\,\sigma _{r},-\sigma _{{r+1}},\dots,-\sigma _{k})$ , gdy $j\in\{ r+1,\dots,\, k\}$ . Również i w tym przypadku więc wszystkie jej wiersze są liniowo zależne, zatem jej rząd wynosi 1.

Podstawowa część teorii Blacka dotyczy modeli, w których $\Sigma>0$ . Wtedy, oczywiście, $\text{rk}\,\Sigma=k$ . Podamy teraz klasyczny rezultat Blacka i współautorów, dotyczący modeli $(\Sigma,\,\mu)\colon\Sigma>0$ z nieograniczoną krótką sprzedażą, przy ważnym i naturalnym założeniu (5.2) z Wykładu V. Rezultat jest sformułowany w języku, który używa oznaczeń

$\alpha=\mu^{{\text{T}}}\Sigma^{{-1}}\mu\,,$

$\beta=\mu^{{\text{T}}}\Sigma^{{-1}}e\ (=e^{{\text{T}}}\Sigma^{{-1}}\mu)\,,$

$\gamma=e^{{\text{T}}}\Sigma^{{-1}}e\,.$

Lemat 6.1

$\alpha\gamma-\beta^{2}>0$ .

Jest to wyznacznik Grama liniowo niezależnego układu wektorów $(\mu,\, e)$ przy iloczynie skalarnym zadanym (w bazie standardowej w $\mathbb{R}^{k}$ ) przez macierz symetryczną i dodatnio określoną $\Sigma^{{-1}}$ .

∎

Uwaga 6.3

Inny możliwy dowód lematu, zaczerpnięty z [23], przypis nr 5 na stronie 1853: $\beta\mu-\alpha e\ne 0$ jako niezerowa ( $\beta$ może się zerować, lecz $\alpha$ nie) kombinacja pary wektorów liniowo niezależnych. Zatem

$0<(\beta\mu-\alpha e)^{{\text{T}}}\,\Sigma^{{-1}}(\beta\mu-\alpha e)=\alpha(\alpha\gamma-\beta^{2})\ \text{ i również }\ \alpha>0\,.$

$\square$

Dwa zdania zapowiedzi. To, co zaraz nastąpi, będzie uogólniało rachunki z Wykładu III. Cały czas należy jednak pamiętać, że tam odcinek $\Delta^{2}$ był automatycznie częścią prostej krytycznej. Teraz zaś prosta, która wyłoni się z twierdzenia poniżej, okaże się nowym bytem wymagającym odrębnego traktowania (szczególnie, gdy używać będziemy mapy Markowitza, która jest la raison d'être dla tej prostej).

Twierdzenie 6.1 (Merton [23], Black i współautorzy)

Przy założeniach $\Sigma>0$ , $\mu\nparallel e$ , zbiór portfeli krytycznych tworzy prostą $\{ x(E)\colon E\in\mathbb{R}\}$ , gdzie

$x(E)\,=\,(\alpha\gamma-\beta^{2})^{{-1}}\,\Sigma^{{-1}}\!\left(\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\mu+\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}e\right)$

(6.2)

i parametr $E$ jest tak dobrany, że $E(x(E))=E$ .

To twierdzenie jest klasyczne i w niniejszych wykładach będzie używane wielokrotnie. Dokładniej, prosta krytyczna sparametryzowana jak we wzorze (6.2) będzie najczęściej przez nas używanym obiektem. Podkreślamy, że o prostych krytycznych Markowitz pisał już w [19], patrz np strona $85^{{1-4}}$ tamże.
(Można w tym miejscu zauważyć, że z kolei w wersji z roku 2000 wykładów [13] prosta krytyczna była tylko pobieżnie wspominana w kilku miejscach bliżej końca tamtych wykładów. Wzoru (6.2) nie było tam w ogóle, bo w jawnej postaci nie był wtedy wykładowcy potrzebny. To pokazuje kolejny raz, jak różna jest koncepcja obecnych wykładów od wcześniejszej koncepcji przyjętej w [13].)

Dowód twierdzenia.

Ten dowód tylko optycznie różni się od oryginalnego dowodu Mertona (głównie tym, że używa wzorów Cramera). Na mocy Twierdzenia 5.1 z Wykładu V, dla każdego punktu krytycznego $x$ w analizie portfelowej istnieją $\lambda _{1},\,\lambda _{2}\in\mathbb{R}$ takie, że $\Sigma x=\lambda _{1}\mu+\lambda _{2}\, e$ . Zapisując to inaczej, $x=\lambda _{1}\Sigma^{{-1}}\mu+\lambda _{2}\Sigma^{{-1}}e$ . Oznaczmy $E(x)=E$ i pomnóżmy tę wektorową równość stronami (z lewej) przez $\mu^{{\text{T}}}$ , następnie zaś stronami, także z lewej, przez $e^{{\text{T}}}$ . Dostajemy układ równań

$\left\{\begin{array}[]{ll}\alpha\lambda _{1}+\beta\lambda _{2}=E&\\ \beta\lambda _{1}+\gamma\lambda _{2}=1\,.&\end{array}\right.$

Dzięki Lematowi 6.1 wiemy, że ten układ ma jedyne rozwiązanie

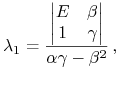$\lambda _{1}=\frac{\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}}{\alpha\gamma-\beta^{2}}\,,$

(6.3)

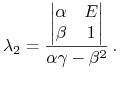$\lambda _{2}=\frac{\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}}{\alpha\gamma-\beta^{2}}\,.$

Dowód twierdzenia jest zakończony.

∎

Pierwszy ze współczynników Lagrange'a pojawiających się w powyższym dowodzie ma ważną interpretację geometryczną; co prawda na płaszczyźnie $\mathbb{R}^{2}(\sigma^{2},\, E)$ , nie zaś na (bardziej kanonicznej!) $\mathbb{R}^{2}(\sigma,\, E)$ .

Obserwacja. 6.1 (interpretacja geometryczna współczynnika $\lambda _{1}$ )

$\lambda _{1}(E)=\frac{1}{2}\frac{d}{dE}\left(\sigma^{2}(x(E))\right)\,.$

Istotnie, liczymy tę pochodną funkcji złożonej jak byśmy z powrotem znaleźli się (na chwilę) na ćwiczeniach z AM II.1:

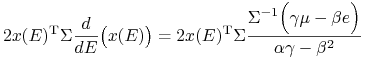$\displaystyle\frac{d}{dE}\left(\sigma^{2}(x(E))\right)$	$\displaystyle=$	$\displaystyle 2x(E)^{{\text{T}}}\Sigma\frac{d}{dE}\bigl(x(E)\bigr)=2x(E)^{{\text{T}}}\Sigma\frac{\Sigma^{{-1}}\Bigl(\gamma\mu-\beta e\Bigr)}{\alpha\gamma-\beta^{2}}$
	$\displaystyle=$	$\displaystyle\frac{2}{(\alpha\gamma-\beta^{2})^{2}}\left(\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\mu^{{\text{T}}}+\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}e^{{\text{T}}}\right)\Sigma^{{-1}}\Bigl(\gamma\mu-\beta e\Bigr)$
	$\displaystyle=$	$\displaystyle\frac{2}{(\alpha\gamma-\beta^{2})^{2}}\left(\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\gamma\alpha+\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}\gamma\beta-\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\beta^{2}-\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}\beta\gamma\right)$
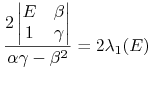	$\displaystyle=$	$\displaystyle\frac{2\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}}{\alpha\gamma-\beta^{2}}=2\lambda _{1}(E)$

∎

(porównaj (6.3) ). Ta własność współczynnika $\lambda _{1}$ będzie przez nas wykorzystywana wielokrotnie. W przyszłości, ze względu na utrwaloną w analizie portfelowej tradycję (i … wbrew zasadzie brzytwy Ockhama), współczynnik ten będzie często oznaczany dosyć dziwnym symbolem $\lambda _{E}$ .

Na co przechodzi prosta krytyczna przy odwzorowaniu Markowitza $\mathcal{M}$ ?

Kłopotu nie ma z drugą składową tego odwzorowania. Na mocy oznaczeń przyjętych w dowodzie Twierdzenia 6.1, $E\big(x(E)\big)=E$ . Sporo trudniej jest policzyć wariancję danego portfela krytycznego $x(E)$ ,

	$\displaystyle\sigma^{2}(x(E))$	$\displaystyle=$	$\displaystyle\frac{1}{(\alpha\gamma-\beta^{2})^{2}}\left(\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\mu^{{\text{T}}}+\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}e^{{\text{T}}}\right)\Sigma^{{-1}}\Sigma\,\,\Sigma^{{-1}}\left(\begin{vmatrix}E&\beta\\ 1&\gamma\end{vmatrix}\mu+\begin{vmatrix}\alpha&E\\ \beta&1\end{vmatrix}e\right)$
		$\displaystyle=$	$\displaystyle\frac{1}{(\alpha\gamma-\beta^{2})^{2}}\big(\gamma(\alpha\gamma-\beta^{2})E^{2}-2\beta(\alpha\gamma-\beta^{2})\big)=\frac{1}{\alpha\gamma-\beta^{2}}(\gamma E^{2}-2\beta E+\alpha)\,.$

Pisząc krótko $\sigma^{2}=\sigma^{2}(x(E))$ , związek ten przybiera postać

$\sigma^{2}(\alpha\gamma-\beta^{2})=\gamma\Big(E^{2}-2\frac{\beta}{\gamma}E+\frac{\alpha}{\gamma}\Big)\,=\,\gamma\Big(E-\frac{\beta}{\gamma}\Big)^{2}+\frac{\alpha\gamma-\beta^{2}}{\gamma}\,,$

albo

$\frac{\sigma^{2}}{a^{2}}-\frac{(E-E_{0})^{2}}{b^{2}}=1\,,$

(6.4)

gdzie

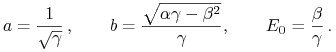$a=\frac{1}{\sqrt{\gamma}}\,,\qquad b=\frac{\sqrt{\alpha\gamma-\beta^{2}}}{\gamma},\qquad E_{0}=\frac{\beta}{\gamma}\,.$

(6.5)

Wzory (6.4) – (6.5) pochodzą także z pracy [23], która dla analizy portfelowej okazuje się być zupełnie fundamentalna. Porównaj też rachunek prowadzony w Wykładzie III w wymiarze $k=2$ , w szczególności przypis nr 1 tamże (w wersji html: przypis nr 3) ).

Wniosek 6.2

$\mathcal{M}$ -obrazem prostej krytycznej jest prawa ( $\sigma>0$ ) gałąź hiperboli (6.4). Jest ona potocznie nazywana pociskiem Markowitza. To jeden z najczęściej używanych terminów w analizie portfelowej.
Prostą krytyczną (6.2) tradycyjnie nazywa się prostą krytyczną Blacka, mimo, że pierwszy raz pojawiła się ona eksplicite w pracy [23]. My też będziemy ją nazywać `Blacka'.
Ściśle biorąc, w pracy [23] portfele leżące na prostej krytycznej – nasze, od Wykładu V, punkty krytyczne w analizie portfelowej – są nazywane frontier portfolios.

Zauważmy w tym momencie, że tangens połowy kąta między asymptotami pocisku Markowitza wynosi

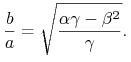$\frac{b}{a}=\sqrt{\frac{\alpha\gamma-\beta^{2}}{\gamma}}.$

(6.6)

Jest to ważna informacja, po którą nie raz będziemy sięgać w dalszych wykładach.

Czy do tej pory widzieliśmy już jakiś pocisk Markowitza, przy tym na kanonicznej płaszczyźnie $\mathbb{R}^{2}(\sigma,\, E)$ ? Tak jest, ,,pociski” tego typu widzieliśmy już, m. in., na Rysunkach 4.4, 4.5 (Wykład IV), czy 6.1 tu wyżej (błękitna gałąź hiperboli).

Uwaga 6.4

Należy mocno podkreślić odmienną naturę pocisków Markowitza przy $k=2$ (np na Rysunkach 4.4 i 4.5) i $k>2$ (np na Rysunkach 4.7 i 6.1). W tym pierwszym przypadku cały zbiór $H$ jest prostą krytyczną, zaś pocisk jest obrazem całej $H$ . Ten pocisk opisywaliśmy już szczegółowo w Wykładzie III.

Natomiast w drugim, przy spełnionych warunkach Twierdzenia 6.1, prosta krytyczna jest bardzo szczupłym podzbiorem $H$ i tylko jej obrazem jest pocisk! Obrazem całej $H$ jest wtedy pocisk oraz cała część płaszczyzny $\mathbb{R}^{2}(\sigma,\, E)$ na prawo od niego.

Przy $k=2$ i $-1<\rho<1$ , tłumaczenie języka z Wykładu III na obecny język Mertona i Blacka jest następujące. Gdy

$\Sigma=\begin{pmatrix}\sigma _{1}^{{\, 2}}&\rho\,\sigma _{1}\sigma _{2}\\ \rho\,\sigma _{1}\sigma _{2}&\sigma _{2}^{{\, 2}}\end{pmatrix},$

wtedy

$\Sigma^{{-1}}=\frac{1}{\sigma _{1}^{{\, 2}}\sigma _{2}^{{\, 2}}(1-\rho^{2})}\begin{pmatrix}\sigma _{2}^{{\, 2}}&-\rho\,\sigma _{1}\sigma _{2}\\ -\rho\,\sigma _{1}\sigma _{2}&\sigma _{1}^{{\, 2}}\end{pmatrix},$

$\gamma=\frac{\sigma _{1}^{{\, 2}}-2\rho\,\sigma _{1}\sigma _{2}+\sigma _{2}^{{\, 2}}}{\sigma _{1}^{{\, 2}}\sigma _{2}^{{\, 2}}(1-\rho^{2})},\quad\text{jako suma wyrazów macierzy }\Sigma^{{-1}},$

$\beta=\frac{\mu _{1}\sigma _{2}^{{\, 2}}+\mu _{2}\sigma _{1}^{{\, 2}}-(\mu _{1}+\mu _{2})\rho\,\sigma _{1}\sigma _{2}}{\sigma _{1}^{{\, 2}}\sigma _{2}^{{\, 2}}(1-\rho^{2})}\quad\text{\big(por. też wzór (3.3) na }E_{0}=E_{0}(\rho)=\frac{\beta}{\gamma}\,\big)\,.$

W takiej sytuacji długości półoś $a$ i $b$ hiperboli znamy już z Wykładu III, wzory (3.5). Zatem, dzięki (6.6),

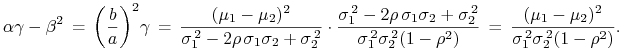$\alpha\gamma-\beta^{2}\,=\,\left(\frac{b}{a}\right)^{2}\!\gamma\,=\,\frac{(\mu _{1}-\mu _{2})^{2}}{\sigma _{1}^{{\, 2}}-2\rho\,\sigma _{1}\sigma _{2}+\sigma _{2}^{{\, 2}}}\cdot\frac{\sigma _{1}^{{\, 2}}-2\rho\,\sigma _{1}\sigma _{2}+\sigma _{2}^{{\, 2}}}{\sigma _{1}^{{\, 2}}\sigma _{2}^{{\, 2}}(1-\rho^{2})}\,=\,\frac{(\mu _{1}-\mu _{2})^{2}}{\sigma _{1}^{{\, 2}}\sigma _{2}^{{\, 2}}(1-\rho^{2})}.$

(6.7)

Uwaga. Opuszczamy tu odpowiedni wzór dla samego parametru $\alpha$ .

Gdy mamy już prostą krytyczną Blacka i jej obraz – pocisk Markowitza, wtedy dość natychmiastowo stwierdzamy, że portfele $x(E)$ są też rozwiązaniami następującego problemu na ekstremum warunkowe

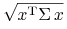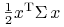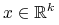minimalizować funkcję $\sqrt{x^{{\text{T}}}\Sigma\, x}$ (czy też $\frac{1}{2}x^{{\text{T}}}\Sigma\, x$ ), $x\in\mathbb{R}^{k}$ , przy ograniczeniach $\left\{\begin{array}[]{ll}\mu^{{\text{T}}}x=E,&\\ e^{{\text{T}}}x=1\,.&\end{array}\right.$

Istotnie, na mocy Twierdzenia 5.1 z Wykładu V, na każdym poziomie $E=\text{const}$ znaleźliśmy już jednego kandydata $x(E)$ na ekstremum warunkowe lokalne. To właśnie jest niezwykłe: $\lambda _{1}\mu+\lambda _{2}\, e$ w Twierdzeniu 5.1 to kombinacja gradientów funkcji warunku i funkcji jedynego ograniczenia budżetowego Blacka. (Jeden ze słuchaczy kilka lat temu zakrzyknął podczas wykładu w tym momencie: `Przecież tu $1+1=3$ !')

Ponieważ przy tym funkcja $x\mapsto x^{{\text{T}}}\Sigma\, x$ jest ściśle wypukła (AM II, GAL 2 oraz – powtórzeniowo – Ćwiczenie 6.4 tu poniżej), więc w istocie ten kandydat $x(E)$ jest minimum warunkowym globalnym – porównaj Optymalizacja 1. Przy każdej ustalonej oczekiwanej stopie zwrotu $E$ znaleźliśmy więc już portfel minimalnego ryzyka $x(E)$ . Przy tym portfele te układają się na prostej, gdy stopa zwrotu przebiega wszystkie à priori możliwe wartości rzeczywiste.

Umiemy zatem minimalizować ryzyko portfela Blacka przy jego ustalonej wartości oczekiwanej! To prawdziwa ,,wartość dodana” wzoru (6.2).¹⁰za który kilku ekonomistów – lecz niestety nie Black, który już wtedy nie żył – dostało w roku 1997 nagrodę Nobla z dziedziny ekonomii

Ćwiczenie 6.4 (w ramach powtórzenia)

Pokazać, że dla macierzy $\Sigma>0$ funkcja $\mathbb{R}^{k}\ni x\mapsto x^{{\text{T}}}\Sigma\, x\in\mathbb{R}$ jest ściśle wypukła, tzn.

$(sx+ty)^{{\text{T}}}\Sigma\,(sx+ty)\le sx^{{\text{T}}}\Sigma\, x+ty^{{\text{T}}}\Sigma\, y\quad\forall x,\, y\in\mathbb{R}^{k}\ \forall s,\, t\ge 0,\ s+t=1,$

zaś ” $=$ ” tylko gdy $x=y\,\,\vee\,\, s=0\,\,\vee\,\, t=0$ .

Dygresja – inne spojrzenie na długość poziomej półosi pocisku Markowitza $a=\frac{1}{\sqrt{\gamma}}$ .

Chodzi o znalezienie wartości (wartości, nie punktu!) globalnego minimum warunkowego funkcji $\sqrt{x^{{\text{T}}}\Sigma\, x}$ przy jednym jedynym warunku budżetowym Blacka $e^{{\text{T}}}x=1$ .

Każdy kandydat na takie ekstremum warunkowe spełnia $\Sigma x=\lambda e$ przy pewnym $\lambda\in\mathbb{R}$ (ekstremalizujemy $\frac{1}{2}x^{{\text{T}}}\Sigma\, x$ zamiast $\sqrt{x^{{\text{T}}}\Sigma\, x}$ ). Wtedy $x=\lambda\Sigma^{{-1}}e$ , więc też $1=\lambda e^{{\text{T}}}\Sigma^{{-1}}e=\lambda\gamma$ , $\lambda=\frac{1}{\gamma}$ . Dostajemy więc jedynego kandydata $x=\frac{\Sigma^{{-1}}e}{\gamma}$ . Z racji ścisłej wypukłości funkcji, którą ekstremalizujemy warunkowo, jest to punkt minimum warunkowego globalnego,

$x_{{\min}}=\frac{\Sigma^{{-1}}e}{\gamma}\,.$

(6.8)

Zgodnie z oczekiwaniami $E(x_{{\min}})=\mu^{{\text{T}}}\frac{\Sigma^{{-1}}e}{\gamma}=\frac{\beta}{\gamma}$ oraz $\sigma^{2}(x_{{\min}})=\frac{1}{\gamma^{2}}e^{{\text{T}}}\Sigma^{{-1}}\Sigma\,\,\Sigma^{{-1}}e=\frac{\gamma}{\gamma^{2}}=\frac{1}{\gamma}$ , tzn. $\sigma(x_{{\min}})=\frac{1}{\sqrt{\gamma}}$ . To zaś jest znany już wzór (6.5) na długość półosi $a$ .

Uwaga 6.5

Załóżmy jeszcze raz przez chwilę, że spółki są tylko dwie i w związku z tym używamy oznaczeń z Wykładu III. Wykluczona jest wtedy tylko, jak pamiętamy, sytuacja $\sigma _{1}=\sigma _{2}$ i $\rho=1$ .

Wzór (6.8) zapisujemy na początek w postaci rozwiniętej

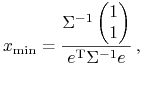$x_{{\min}}=\frac{\Sigma^{{-1}}\begin{pmatrix}1\\ 1\end{pmatrix}}{e^{{\text{T}}}\Sigma^{{-1}}e}\,,$

po czym, po prawej stronie, mnożymy macierze $\Sigma^{{-1}}$ stojące w liczniku i mianowniku przez $\det\Sigma$ . Po tej czynności mamy już w liczniku i mianowniku macierz dopełnień algebraicznych macierzy $\Sigma$ zamiast samej macierzy $\Sigma^{{-1}}$ .¹¹Wzór na $\Sigma^{{-1}}$ przy $k=2$ pojawił się już w Uwadze 6.4 powyżej. To szybko prowadzi do wzoru

$x_{{\min}}=\Big(\sigma _{1}^{{\, 2}}-2\rho\,\sigma _{1}\sigma _{2}+\sigma _{2}^{{\, 2}}\Big)^{{-1}}\begin{pmatrix}\sigma _{2}^{{\, 2}}-\rho\,\sigma _{1}\sigma _{2}\\ \sigma _{1}^{{\, 2}}-\rho\,\sigma _{1}\sigma _{2}\end{pmatrix}\,,$

w którego pierwszej składowej rozpoznajemy¹²nie może być inaczej, bo cały czas mówimy o jednej i tej samej minimalizacji ryzyka portfeli Blacka wielkość $x_{{1,0}}$ z wzoru z Wykładu III (zaraz za Uwagą 3.2).

Po wprowadzeniu i (wstępnym) przedyskutowaniu nieograniczonej krótkiej sprzedaży, w naszym ujęciu analizy portfelowej wyodrębnione są teraz dwa oddzielne aspekty: aspekt Markowitza, oznaczany M, z portfelami dopuszczalnymi leżącymi w (gdy ilość spółek w modelu jest $k$ ) sympleksie $\Delta^{k}$ , oraz aspekt Blacka, oznaczany B, z portfelami dopuszczalnymi leżącymi na hiperpłaszczyźnie $H$ zdefiniowanej (jeszcze w Wykładzie II) wzorem (2.2).
Dla rozróżnienia aspektów będziemy już do końca tych wykładów używać skrótów M oraz B.

W aspekcie M wprowadziliśmy, nie etykietkując tego wtedy (Wykład III) jawnie literą M, pojęcia granic: minimalnej $F_{{\min}}$ oraz maksymalnej $F_{{\max}}$ . Pierwsze nasuwające się pytanie to, czy te granice mają swoje analogi w aspekcie B.

Otóż jeśli chodzi o $F_{{\max}}$ , to nie, bo zbiory liniowe $\mathcal{M}(H)\cap\{ E=\text{const}\}$ typowo są poziomymi półprostymi skierowanymi ,,w prawo”. (Inaczej jest, gdy $k=2$ lub gdy czasem model jest choćby częściowo zdegenerowany.) Jeśli natomiast chodzi o $F_{{\min}}$ , to tak, bo definicja

$F_{{\min}}\overset{\text{def}}{=}\Big\{\text{zbiór lewych krańców zbiorów liniowych }\mathcal{M}(H)\cap\{ E=\text{const}\}\Big\}$

ma także sens w aspekcie B i oznacza po prostu, że ta nowa granica minimalna jest pociskiem Markowitza!

Ważną rzeczą w analizie portfelowej jest porównywanie granic minimalnych w aspektach M i B, zaś szczególnie: porównywanie ich tzw. części efektywnych (ang. `efficient'), o czym dużo będziemy mówić w dalszych wykładach. Teraz, dla przykładu, porównajmy te obiekty na Rysunku 6.1 powyżej. $F_{{\min}}$ w aspekcie M to suma dwóch łuków hiperbol $\mathcal{M}(\overline{e_{1}\, e_{2}})\cup\mathcal{M}(\overline{e_{1}\, e_{3}})$ (niebieskiego i czerwonego). Natomiast $F_{{\min}}$ w aspekcie B to, jak już było wspomniane, błękitny pocisk – obraz prostej krytycznej w rozważanym przykładzie.

Ćwiczenie 6.5

Znaleźć granice minimalne w aspektach M i B w przykładzie zilustrowanym na Rysunku 4.7 w Wykładzie IV.

(Uwaga. Tamten rysunek wykonany jest na płaszczyźnie $\mathbb{R}^{2}(\sigma^{2},\, E)$ , chodzi tu więc o warianty granic minimalnych pojawiające się w wyniku użycia odwzorowania $\widetilde{\mathcal{M}}$ zamiast odwzorowania $\mathcal{M}$ .)

Przykład 6.3 (obliczenia prostej krytycznej przy pomocy Twierdzenia 6.1 – kontynuacja Przykładu 5.1 z Wykładu V)

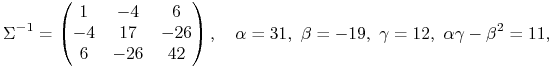$\Sigma^{{-1}}=\begin{pmatrix}1&-4&6\\ -4&17&-26\\ 6&-26&42\end{pmatrix},\quad\alpha=31,\ \beta=-19,\ \gamma=12,\ \alpha\gamma-\beta^{2}=11,$

Zgodnie ze wzorem (6.2),

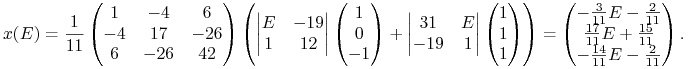$x(E)=\frac{1}{11}\begin{pmatrix}1&-4&6\\ -4&17&-26\\ 6&-26&42\end{pmatrix}\left(\begin{vmatrix}E&-19\\ 1&12\end{vmatrix}\begin{pmatrix}1\\ 0\\ -1\end{pmatrix}+\begin{vmatrix}31&E\\ -19&1\end{vmatrix}\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\right)=\begin{pmatrix}-\frac{3}{11}E-\frac{2}{11}\\ \frac{17}{11}E+\frac{15}{11}\\ -\frac{14}{11}E-\frac{2}{11}\end{pmatrix}.$

W szczególności

$x\left(-\frac{15}{17}\right)=\begin{pmatrix}\frac{1}{17}\\ 0\\ \frac{16}{17}\end{pmatrix}\quad\text{ oraz }\quad x\left(-\frac{2}{3}\right)=\begin{pmatrix}0\\ \frac{1}{3}\\ \frac{2}{3}\end{pmatrix},$

co widać na Rysunku 5.1 w Wykładzie V (miejsca przecięcia prostej krytycznej z bokami trójkąta). Pocisk Markowitza (albo też: parabola w płaszczyźnie $\mathbb{R}^{2}(\sigma^{2},\, E)$ ) ma tu równanie $\sigma^{2}=\frac{12}{11}E^{2}+\frac{38}{11}E+\frac{31}{11}$ .

To uzupełnia Przykład 5.1 w Wykładzie V. Mamy (wreszcie) już całościowy opis obiektów składających się na przykład Krzyżewskiego – i wkrótce to wykorzystamy.

Dla utrwalenia wzorów poznanych na tym wykładzie proponujemy wrócić jeszcze do Rysunku 6.1 i danych (6.1), które go generują. Naśladując rachunki z Przykładu 6.3, policzmy tu prostą krytyczną, która w mapie ryzyko – wartość oczekiwana daje błękitny pocisk Markowitza na Rysunku 6.1.

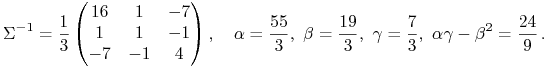$\Sigma^{{-1}}=\frac{1}{3}\begin{pmatrix}16&1&-7\\ 1&1&-1\\ -7&-1&4\end{pmatrix},\quad\alpha=\frac{55}{3},\ \beta=\frac{19}{3},\ \gamma=\frac{7}{3},\ \alpha\gamma-\beta^{2}=\frac{24}{9}\,.$

Stosując znowu wzór (6.2),

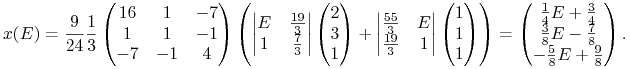$x(E)=\frac{9}{24}\frac{1}{3}\begin{pmatrix}16&1&-7\\ 1&1&-1\\ -7&-1&4\end{pmatrix}\left(\begin{vmatrix}E&\frac{19}{3}\\ 1&\frac{7}{3}\end{vmatrix}\begin{pmatrix}2\\ 3\\ 1\end{pmatrix}+\begin{vmatrix}\frac{55}{3}&E\\ \frac{19}{3}&1\end{vmatrix}\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\right)=\begin{pmatrix}\frac{1}{4}E+\frac{3}{4}\\ \frac{3}{8}E-\frac{7}{8}\\ -\frac{5}{8}E+\frac{9}{8}\end{pmatrix}.$

Ćwiczenie 6.6

1. Upewnić się, że ta prosta krytyczna nie przecina sympleksu standardowego $\Delta^{3}$ , czyli, że tutaj żaden portfel krytyczny Blacka nie jest Markowitza.

2. Upewnić się też, że wartość oczekiwana $E$ nie jest stała na tej prostej krytycznej.

Wskazówka:

Nietrudno policzyć wektor prędkości $x^{{\prime}}(E)$ .

Ćwiczenie 6.7

Czy zawsze na prostej (6.2) parametr $E$ zmienia się (nie jest stały)?

Wskazówka:

Nietrudno zróżniczkować po $E$ wzór (6.2) na $x(E)$ . Dlaczego wynik jest zawsze wektorem niezerowym?

Zajmijmy się teraz dokładniej ostatnim pytaniem nr 4 w Ćwiczeniu 6.1 na początku tego wykładu. Po wykonaniu Ćwiczenia 6.6, jak teraz operatywnie zapisać proste–poziomice wartości $E$ na płaszczyźnie $H$ , i to w powiązaniu z parametrycznym opisem tej prostej krytycznej?

Po prostu policzyć iloczyn wektorowy

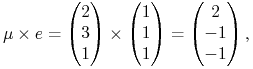$\mu\times e=\begin{pmatrix}2\\ 3\\ 1\end{pmatrix}\times\begin{pmatrix}1\\ 1\\ 1\end{pmatrix}=\begin{pmatrix}2\\ -1\\ -1\end{pmatrix},$

po czym zapisać (wszystkie!) punkty płaszczyzny $H$ jako

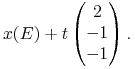$x(E)+t\begin{pmatrix}2\\ -1\\ -1\end{pmatrix}.$

Ustalając tu $E$ i zmieniając $t$ , właśnie dostaje się poziomicę trafiającą prostą krytyczną w punkcie (portfelu Blacka) $x(E)$ .

Uwaga 6.6

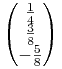Nie należy sądzić, że te poziomice wartości oczekiwanej $E$ są prostopadłe do prostej krytycznej! Tną one prostą krytyczną ukośnie pod ustalonym kątem. Np w rozważanym przykładzie wektor wyznaczający kierunek prostej krytycznej $\begin{pmatrix}\frac{1}{4}\\ \frac{3}{8}\\ -\frac{5}{8}\end{pmatrix}$ właśnie nie jest prostopadły de wektora $\mu\times e$ , tylko tworzy z nim kąt około $68\frac{1}{3}$ stopni.

(Jak wylicza się taką rozwartość kąta? Pożądane byłoby tu zaznaczyć na kartce papieru trzy wierzchołki pewnego trójkąta równobocznego o boku długości $\sqrt{2}$ , nazwać je $e_{1}^{{\prime}},\, e_{2}^{{\prime}},\, e_{3}^{{\prime}}$ , jako obrazy wierzchołków $\Delta^{3}$ przy pewnej jednoznacznie już wyznaczonej izometrii, po czym narysować na kartce obraz prostej krytycznej w tej izometrii oraz obrazy poziomic parametru $E$ . Nie symbolicznie, lecz realnie. Tak, jak one naprawdę leżą na $H$ względem wierzchołków trójkąta $\Delta^{3}$ . Tutaj rysowanie jako wierna izometria.)

Ćwiczenie 6.8

Rozwiązać ostatnią część (nr 4) Ćwiczenia 6.1.

Wskazówka:

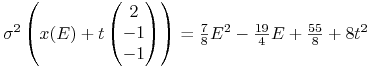$\sigma^{2}\left(x(E)+t\begin{pmatrix}2\\ -1\\ -1\end{pmatrix}\right)=\frac{7}{8}E^{2}-\frac{19}{4}E+\frac{55}{8}+8t^{2}$ . Gdzie zatem szukać portfela dublującego dany portfel Markowitza co do ryzyka i wartości oczekiwanej? Czy można go narysować ?

Ćwiczenie 6.9

Pokazać, że, przynajmniej w wymiarze $k=3$ , z powyższych ćwiczeń wyłania się już ogólny sposób znajdowania ,,fałszywych portfeli Markowitza” dublujących te ostatnie co do ryzyka i wartości oczekiwanej. Tak więc, dla danego portfela Markowitza – jego ,,fałszywy” odpowiednik.

Oczywiście najciekawiej jest, gdy – jak tutaj – prosta krytyczna nie tnie trójkąta $\Delta^{3}$ . Co się dzieje z ,,fałszywymi” portfelami Markowitza, gdy prosta krytyczna jednak tnie sympleks (mieliśmy już takie przykłady; czy wszystkie ,,fałszywe” są wtedy naprawdę fałszywe)?

Wskazówka:

Pokazać, wykorzystując wzór (6.2), że, przy parametrze $E$ traktowanym jako stała, w trójmianie kwadratowym od $t$ , $\sigma^{2}\big(x(E)+t\,\mu\times e\big)$ , nie ma wyrazu z $t^{1}$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Analiza Portfelowa i Rynki Kapitałowe 1

6. Wykład VI, 6.XI.2009.

Przykład 6.1

Uwaga 6.1

Wniosek 6.1

Uwaga 6.2

Ćwiczenie 6.1

Przykład 6.2 (kontynuacja Rysunku 3.2)

Ćwiczenie 6.2

Ćwiczenie 6.3 (sprawdzające)

Lemat 6.1

Uwaga 6.3

Twierdzenie 6.1 (Merton [23], Black i współautorzy)

Dowód twierdzenia.

Wniosek 6.2

Uwaga 6.4

Ćwiczenie 6.4 (w ramach powtórzenia)

Uwaga 6.5

Ćwiczenie 6.5

Przykład 6.3 (obliczenia prostej krytycznej przy pomocy Twierdzenia 6.1 – kontynuacja Przykładu 5.1 z Wykładu V)

Ćwiczenie 6.6

Ćwiczenie 6.7

Uwaga 6.6

Ćwiczenie 6.8

Ćwiczenie 6.9