7. Wykład VII, 13.XI.2009
Uwaga 7.1
Osoby, które zajęły się wskazówką do [ostatniego w poprzednim wykładzie]
Ćwiczenia 6.9, wiedzą już, dlaczego zeruje się tam współczynnik przy ![]() we wzorze na wariancję portfeli na poziomicy parametru
we wzorze na wariancję portfeli na poziomicy parametru ![]() :
:
por. wzór (6.2) w Wykładzie VI. Powód bardziej prozaiczny
(choć związany z poprzednim, te powody wzajemnie się przenikają) jest taki:
dyskutowany trójmian kwadratowy od ![]() musi przyjmować swoje minimum przy
musi przyjmować swoje minimum przy
![]() , bo właśnie wtedy trafiamy w portfel
, bo właśnie wtedy trafiamy w portfel ![]() , który minimalizuje
ryzyko (a więc i wariancję) na poziomicy wartości
, który minimalizuje
ryzyko (a więc i wariancję) na poziomicy wartości ![]() , jak to było
wyjaśniane i komentowane w Wykładzie VI.
, jak to było
wyjaśniane i komentowane w Wykładzie VI.
Wspomniane osoby wiedzą też, że ta czysto kwadratowa (bez przesunięcia
powodowanego wyrazem z ![]() ) zależność wariancji od
) zależność wariancji od ![]() jest taka sama
(jeśli chodzi o zmienność) na każdej z poziomic parametru
jest taka sama
(jeśli chodzi o zmienność) na każdej z poziomic parametru ![]() tnących
prostą krytyczną, tzn., że współczynnik przy
tnących
prostą krytyczną, tzn., że współczynnik przy ![]() nie zależy
od
nie zależy
od ![]() . Istotnie,
. Istotnie,
Powtarzamy, jeszcze raz po Wykładzie VI: równanie pocisku
Markowitza w każdym niezdegenerowanym przypadku powstaje przez
podstawienie szczególnych wartości ![]() do ogólnego równania (6.4).
do ogólnego równania (6.4).
(Jeśli ktoś ogólne wzory lubi mniej niż konkretne obliczenia,
ten liczy bezpośrednio wariancje portfeli krytycznych ![]() .
Np w przykładzie Krzyżewskiego (rozpoczętym w Wykładzie V,
kontynuowanym w Wykładzie VI)
.
Np w przykładzie Krzyżewskiego (rozpoczętym w Wykładzie V,
kontynuowanym w Wykładzie VI)
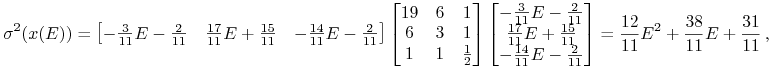 |
jak w Przykładzie 6.3. W przyszłości nie będziemy już precyzować sposobu, w jaki policzony został pocisk Markowitza w niezdegenerowanym modelu Blacka.)
Uwaga 7.2 (i zarazem ćwiczenie)
Wiemy już doskonale, że niezdegenerowane macierze ![]() wraz z niestałymi
wektorami
wraz z niestałymi
wektorami ![]() zawsze generują pociski Markowitza jako granice minimalne
w modelach Blacka. Jednakże nie zawsze na odwrót! Oto przykład modelu Blacka,
w którym macierz kowariancji jest tylko nieujemnie określona (więc teoria
Blacka jako taka się nie stosuje), a mimo to granica minimalna jest w nim
gałęzią najprawdziwszej niezdegenerowanej hiperboli.
zawsze generują pociski Markowitza jako granice minimalne
w modelach Blacka. Jednakże nie zawsze na odwrót! Oto przykład modelu Blacka,
w którym macierz kowariancji jest tylko nieujemnie określona (więc teoria
Blacka jako taka się nie stosuje), a mimo to granica minimalna jest w nim
gałęzią najprawdziwszej niezdegenerowanej hiperboli.
W modelu występują trzy spółki (![]() ). Macierz kowariancji zmiennych
stóp zwrotu ze spółek oraz wektor wartości oczekiwanych stóp zwrotu
ze spółek to
). Macierz kowariancji zmiennych
stóp zwrotu ze spółek oraz wektor wartości oczekiwanych stóp zwrotu
ze spółek to
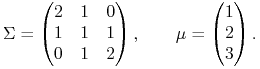 |
(7.1) |
Ta macierz jest tylko nieujemnie określona (stosuje się wiedza z Wykładu II,
wszystkie minory centralne w ![]() są nieujemne). Nie jest dodatnio określona
– jej wyznacznik znika.
są nieujemne). Nie jest dodatnio określona
– jej wyznacznik znika.
Jest pouczającym (i niezbyt łatwym) ćwiczeniem policzyć w tym modelu obraz
![]() odwzorowania Markowitza. Odpowiedzią okazuje się być prawa
(
odwzorowania Markowitza. Odpowiedzią okazuje się być prawa
(![]() ) gałąź pewnej niezdegenerowanej hiperboli –
zbiór bez wnętrza na płaszczyźnie (mimo, że wymiar modelu
jest trzy; to jeszcze inna osobliwość tego przykładu).
) gałąź pewnej niezdegenerowanej hiperboli –
zbiór bez wnętrza na płaszczyźnie (mimo, że wymiar modelu
jest trzy; to jeszcze inna osobliwość tego przykładu).
Obliczenie pokaże, że tym obrazem jest prawa gałąź hiperboli
![]() . Jednak równocześnie … inne
obliczenie pokazuje, że wszystkie portfele
Blacka
. Jednak równocześnie … inne
obliczenie pokazuje, że wszystkie portfele
Blacka ![]() są w tym przykładzie krytyczne:
są w tym przykładzie krytyczne:
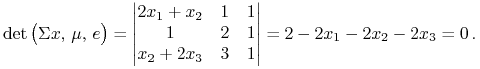 |
Czyli – porównaj Wykład VI – wszystkie w ogóle portfele
relatywnie (tj przy ![]() ) minimalizują ryzyko!
Ich obrazy leżą zatem na granicy minimalnej w tym modelu
Blacka. Dziwne to wszystko, nieprawdaż?
) minimalizują ryzyko!
Ich obrazy leżą zatem na granicy minimalnej w tym modelu
Blacka. Dziwne to wszystko, nieprawdaż?
Trzeba zajmować się obiema składowymi odwzorowania Markowitza w punkcie – portfelu Blacka. Zajmijmy się najpierw wartością oczekiwaną portfela:
więc ![]() (za chwilę ten związek okaże się pomocny).
Teraz pierwsza składowa odwzorowania, a dokładniej mówiąc –
wariancja portfela:
(za chwilę ten związek okaże się pomocny).
Teraz pierwsza składowa odwzorowania, a dokładniej mówiąc –
wariancja portfela:
Związek podany we wskazówce zachodzi więc dla każdego portfela Blacka; wariancja portfela w tym przykładzie zależy tylko od wartości oczekiwanej portfela(!)
Wyjaśnienie tego zjawiska jest następujące: forma kwadratowa
związana z macierzą ![]() jest dodatnio określona na wektorach
reprezentowanych przez punkty z płaszczyzny afinicznej
jest dodatnio określona na wektorach
reprezentowanych przez punkty z płaszczyzny afinicznej ![]() ,
i również kres dolny jej wartości na tych wektorach jest
dodatni (równy 1, jak wynika z powyższego rachunku).
Kłopot sprawiałyby tylko pewne wektory o sumie składowych
zero, gdyż takie są w tym przykładzie wektory własne macierzy
,
i również kres dolny jej wartości na tych wektorach jest
dodatni (równy 1, jak wynika z powyższego rachunku).
Kłopot sprawiałyby tylko pewne wektory o sumie składowych
zero, gdyż takie są w tym przykładzie wektory własne macierzy
![]() odpowiadające wartości własnej 0. Jednakże takie wektory
w analizie portfelowej nie są używane.
odpowiadające wartości własnej 0. Jednakże takie wektory
w analizie portfelowej nie są używane.
W rozwiązaniu łamigłówki podanej w Uwadze 7.2 wspomnieliśmy, że suma składowych portfela nigdy nie jest zero. Otóż jest pewien wyjątek, dopuszczany w tzw. podejściu Lintnera, o czym wspominamy w Wykładzie IX. Takie inwestowanie à la Lintner, z zerową czy nawet ujemną sumą składowych portfela, w teorii Blacka nie jest dopuszczane.
Portfele efektywne (w źródle) i granica efektywna (w obrazie)
Wprowadzimy za chwilę dwa kluczowe w analizie portfelowej pojęcia:
efektywności danego portfela i granicy efektywnej w danym modelu.
Przewijają się one przez teksty poświęcone analizie portfelowej
od samego jej historycznego początku – porównaj np obszerny cytat
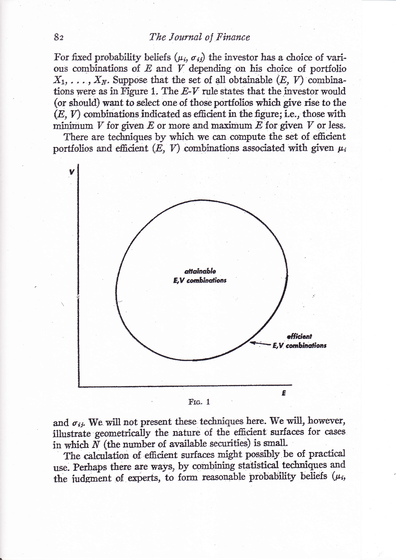
z [19] w Wykładzie II (,,the set of efficient ![]() combinations”), czy też reprodukcję strony 82 z tej samej
pracy na Rysunku 7.2 poniżej. Już na tej reprodukcji można
oglądać pewną (uproszczoną, wyidealizowaną) granicę efektywną!
combinations”), czy też reprodukcję strony 82 z tej samej
pracy na Rysunku 7.2 poniżej. Już na tej reprodukcji można
oglądać pewną (uproszczoną, wyidealizowaną) granicę efektywną!
By zobaczyć te pojęcia w odpowiedniej perspektywie, chcemy
przez chwilę włączyć zmienne losowe pojawiające się
w analizie portfelowej w pewien szerszy schemat. Zbiory portfeli
Markowitza ![]() i portfeli Blacka
i portfeli Blacka ![]() to przykłady
wachlarzy możliwych scenariuszy inwestycyjnych,
oznaczanych ogólnie
to przykłady
wachlarzy możliwych scenariuszy inwestycyjnych,
oznaczanych ogólnie ![]() . Elementy wachlarza,
np portfele akcji (choć mogą to być też inwestycje w obligacje,
nieruchomości, instrumenty pochodne …) mają przypisane do
siebie zmienne losowe wyrażające możliwe stopy zysku z
danego scenariusza w ustalonym okresie inwestycyjnym:
. Elementy wachlarza,
np portfele akcji (choć mogą to być też inwestycje w obligacje,
nieruchomości, instrumenty pochodne …) mają przypisane do
siebie zmienne losowe wyrażające możliwe stopy zysku z
danego scenariusza w ustalonym okresie inwestycyjnym:
gdzie
-
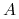 – scenariusz, albo plan,
– scenariusz, albo plan, -
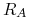 – zmienna losowa wyrażająca stopę zysku w ustalonym
okresie inwestycyjnym z tego scenariusza, planu …
– zmienna losowa wyrażająca stopę zysku w ustalonym
okresie inwestycyjnym z tego scenariusza, planu …
Zupełnie analogicznie do tego, jak ustalonemu portfelowi akcji ![]() Markowitz czy Black przypisuje zmienną losową
Markowitz czy Black przypisuje zmienną losową ![]() –
stopę zwrotu z tego portfela.
–
stopę zwrotu z tego portfela.
Dla zmiennych losowych generalnie istnieją różne miary ryzyka, z których
jedną jest odchylenie standardowe ![]() . Ustalmy na pewien czas jedną
z takich miar
. Ustalmy na pewien czas jedną
z takich miar ![]() .
.
Definicja 7.1 (relacja porównująca scenariusze inwestycyjne)
Jest to częściowy porządek w wachlarzu ![]() .
(Oczywiście, ogólnie nie każde dwa scenariusze można porównywać
taką relacją
.
(Oczywiście, ogólnie nie każde dwa scenariusze można porównywać
taką relacją ![]() .)
.)
Mówimy, że scenariusz ![]() jest nie lepszy niż
jest nie lepszy niż ![]() , albo,
że
, albo,
że ![]() dominuje
dominuje ![]() (względnie:
(względnie: ![]() jest dominowany przez
jest dominowany przez ![]() ).
).
Definicja 7.2 (scenariusz efektywny)
Mówimy, że scenariusz ![]() jest efektywny
w sensie danej relacji
jest efektywny
w sensie danej relacji ![]() ,
gdy
,
gdy ![]() nie jest dominowany przez żaden scenariusz
nie jest dominowany przez żaden scenariusz
![]() taki, że przynajmniej jedna z nierówności
w Definicji 7.1 jest ostra.
taki, że przynajmniej jedna z nierówności
w Definicji 7.1 jest ostra.
Interpretacja geometryczna Definicji 7.2.
Używając analogu odwzorowania Markowitza, tzn. rysując ,,mapy”
na płaszczyźnie ![]() , scenariusz
, scenariusz ![]() jest
efektywny w sensie
jest
efektywny w sensie ![]() gdy nie istnieje scenariusz
gdy nie istnieje scenariusz ![]() taki, że punkt
taki, że punkt
![]() leży w
domkniętym kątowniku `południowo-wschodnim' o wierzchołku
leży w
domkniętym kątowniku `południowo-wschodnim' o wierzchołku
![]() bez samego tego wierzchołka –
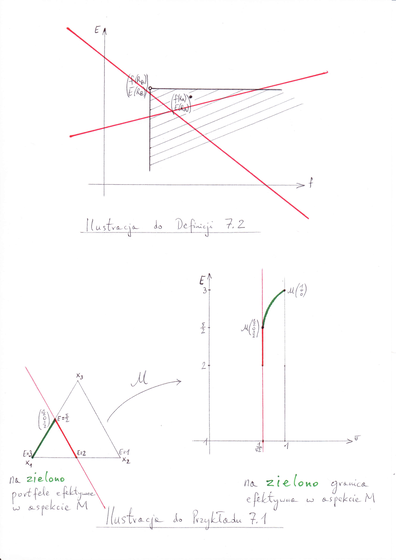
patrz górna część Rysunku 7.1 (nieistnienie wyrażone
jest czerwonym przekreśleniem jak przy znaku zakazu).
bez samego tego wierzchołka –
patrz górna część Rysunku 7.1 (nieistnienie wyrażone
jest czerwonym przekreśleniem jak przy znaku zakazu).
To samo można też wyrazić dualnie: ma nie istnieć
![]() , którego obraz leżałby w domkniętym kątowniku [uwaga!]
północno-zachodnim o wierzchołku w obrazie
, którego obraz leżałby w domkniętym kątowniku [uwaga!]
północno-zachodnim o wierzchołku w obrazie ![]() i był
różny od obrazu
i był
różny od obrazu ![]() (czyli: leżałby w domkniętym kątowniku
j. w. bez wierzchołka). [W wersji pdf ilustrujący tę
interpretację Rysunek 7.1 dopiero otwiera następną stronę.]
(czyli: leżałby w domkniętym kątowniku
j. w. bez wierzchołka). [W wersji pdf ilustrujący tę
interpretację Rysunek 7.1 dopiero otwiera następną stronę.]
Należy zauważyć, że spójna i dostatecznie szeroko akceptowana
teoria rozwinęła się jedynie na bazie miary ryzyka ![]() (odchylenie standardowe zmiennej losowej).
(odchylenie standardowe zmiennej losowej).
Ponadto w analizie portfelowej najczęściej używamy
wachlarzy – zbiorów portfeli akcji: Markowitza (wtedy
![]() , aspekt M z Wykładu VI),
względnie Blacka (wtedy
, aspekt M z Wykładu VI),
względnie Blacka (wtedy ![]() , aspekt B
z Wykładu VI).13Najczęściej, to nie znaczy, że jedynie.
Już przy analizie modelu Tobina, co nastąpi w Wykładzie XI,
mielibyśmy inny typ wachlarza. Również przy ogólnym
modelu Markowitza, o którym w tych wykładach nie mówimy,
dodatkowe ograniczenia na udziały akcji spółek w portfelach
dopuszczalnych przekładałyby się na inne, nowe wachlarze.
, aspekt B
z Wykładu VI).13Najczęściej, to nie znaczy, że jedynie.
Już przy analizie modelu Tobina, co nastąpi w Wykładzie XI,
mielibyśmy inny typ wachlarza. Również przy ogólnym
modelu Markowitza, o którym w tych wykładach nie mówimy,
dodatkowe ograniczenia na udziały akcji spółek w portfelach
dopuszczalnych przekładałyby się na inne, nowe wachlarze.
Powiemy, specyfikując Definicję 7.2, że portfel ![]() , w aspekcie
M lub też B, jest efektywny jeśli jest on
efektywny jako scenariusz inwestycyjny przy wachlarzu
, w aspekcie
M lub też B, jest efektywny jeśli jest on
efektywny jako scenariusz inwestycyjny przy wachlarzu ![]() (w aspekcie M) lub przy wachlarzu
(w aspekcie M) lub przy wachlarzu ![]() (w aspekcie B) i mierze ryzyka zawsze
(w aspekcie B) i mierze ryzyka zawsze ![]() .
.
Portfele efektywne są najważniejsze w analizie portfelowej. Nie jest je trudno znaleźć w aspekcie B (patrz np Rysunek 7.6 poniżej), natomiast w aspekcie M – ogólnie bardzo trudno (patrz np Rysunek 7.5 poniżej). Większa część pozostałych wykładów jest poświęcona szukaniu bądź wszystkich, bądź specjalnych (optymalnych w różnych sensach), portfeli efektywnych. By, tytułem przykładu, już tutaj zilustrować wagę portfeli efektywnych – można rekomendować fragment z pracy [23] podany za Przykładem 13.1 w Wykładzie XIII.14portfele i ich obrazy są tam co prawda mylone, lecz to mało znaczący szczegół
Definicja 7.3
Granica efektywna ![]() , w każdym z aspektów,
to obraz przy odwzorowaniu Markowitza
, w każdym z aspektów,
to obraz przy odwzorowaniu Markowitza ![]() wszystkich
portfeli efektywnych w rozważanym aspekcie.
wszystkich
portfeli efektywnych w rozważanym aspekcie.
Uwaga 7.3
Podkreślamy bardzo mocno, że ![]() jest określona w
danym aspekcie: M albo B. Przy zmianie
aspektu może ona zmieniać się dramatycznie, jak pokazane w Przykładzie 7.1
poniżej.
jest określona w
danym aspekcie: M albo B. Przy zmianie
aspektu może ona zmieniać się dramatycznie, jak pokazane w Przykładzie 7.1
poniżej.
Obserwacja. 7.1 W każdym z aspektów, B czy też M,
Istotnie, warunkiem koniecznym, by portfel ![]() był efektywny, jest
minimalizowanie przez
był efektywny, jest
minimalizowanie przez ![]() odchylenia standardowego
odchylenia standardowego ![]() wśród
wszystkich portfeli
wśród
wszystkich portfeli ![]() (lecz tylko dopuszczanych w danym aspekcie!)
takich, że
(lecz tylko dopuszczanych w danym aspekcie!)
takich, że ![]() – porównaj interpretacja geometryczna
Definicji 7.2. W przeciwnym przypadku obraz portfela
– porównaj interpretacja geometryczna
Definicji 7.2. W przeciwnym przypadku obraz portfela ![]() leżałby na górnej (`północnej') granicy południowo-wschodnigo
kątownika wyznaczonego przez pewien
leżałby na górnej (`północnej') granicy południowo-wschodnigo
kątownika wyznaczonego przez pewien ![]() i byłby
przy tym różny od wierzchołka
i byłby
przy tym różny od wierzchołka ![]() tego kątownika.
tego kątownika.
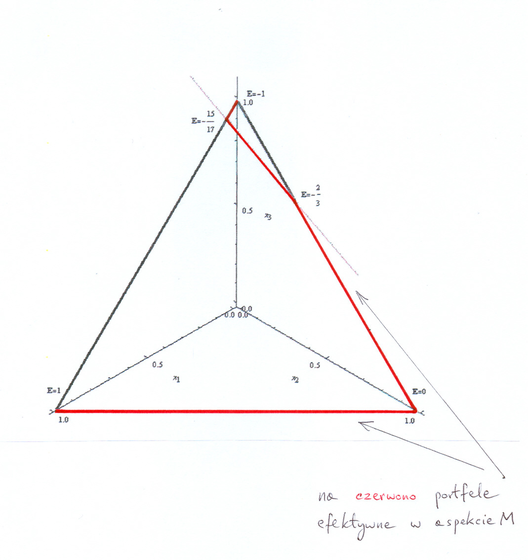
Przykład 7.1
Granicą efektywną ![]() w modelu
w modelu
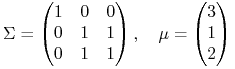 |
rozważanym w aspekcie M jest domknięty łuk hiperboli
– obraz (też zielony) zielonej połowy boku ![]() na Rysunku 7.1 w jego dolnej części. Uzasadnienie mieści się
w samym tym rysunku części granicy
na Rysunku 7.1 w jego dolnej części. Uzasadnienie mieści się
w samym tym rysunku części granicy ![]() na płaszczyźnie
na płaszczyźnie
![]() . Zielone punkty granicy minimalnej nie są
przez nic zdominowane – nie są w cieniu żadnego innego punktu
tej granicy. Natomiast czerwone punkty już są zdominowane –
przez czerwone położone nad nimi! Nienarysowane punkty granicy
minimalnej (mające wartości
. Zielone punkty granicy minimalnej nie są
przez nic zdominowane – nie są w cieniu żadnego innego punktu
tej granicy. Natomiast czerwone punkty już są zdominowane –
przez czerwone położone nad nimi! Nienarysowane punkty granicy
minimalnej (mające wartości ![]() między 1 i 2) są zdominowane
przez czerwone punkty.
między 1 i 2) są zdominowane
przez czerwone punkty.
(Porównaj też wcześniejszą analizę tego samego modelu, robioną pod innym kątem, w Wykładzie IV).
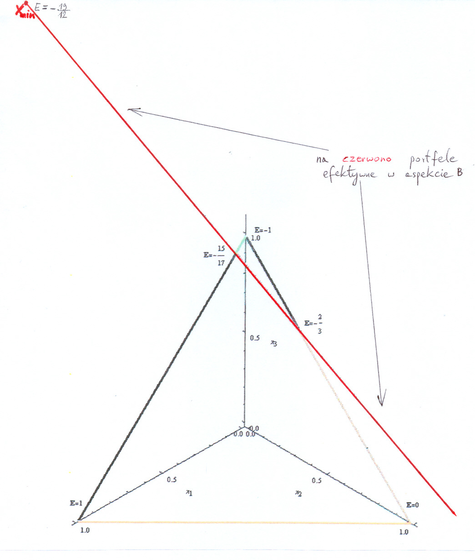
Natomiast ![]() w tym samym modelu
rozważanym w aspekcie B! Istotnie,
w tym samym modelu
rozważanym w aspekcie B! Istotnie, ![]() jest wtedy
całą prostą
jest wtedy
całą prostą ![]() – obrazem prostej
– obrazem prostej
![]() (obie te proste są obecne na
Rysunku 7.1). Tymczasem każdy portfel z tej ostatniej prostej
jest zdominowany przez jakikolwiek portfel na niej mający
większą wartość oczekiwaną. Brak zatem portfeli
efektywnych w sensie Definicji 7.2.
(obie te proste są obecne na
Rysunku 7.1). Tymczasem każdy portfel z tej ostatniej prostej
jest zdominowany przez jakikolwiek portfel na niej mający
większą wartość oczekiwaną. Brak zatem portfeli
efektywnych w sensie Definicji 7.2.
Uwaga 7.4 (ostrzeżenie)
W książce [10] na stronie 138, za portfel efektywny uznawany jest portfel, dla którego NIE istnieje portfel, mający niższe ryzyko przy danej oczekiwanej stopie zwrotu,
lub
mający wyższą oczekiwaną stopę zwrotu przy danym ryzyku.
By uniknąć patologii i być w zgodności z Definicją 7.2,
podkreślone słowo danej należałoby zastąpić przez
,,nie mniejszej”, zaś podkreślone słowo danym
przez ,,nie większym”.
To samo należałoby też uczynić w definicji efektywności portfela
podanej w pracy [26] (linie 2-4 na stronie 278), gdzie
stoi wyraźnie: ”… a portfolio is efficient if none other gives
either (a) a higher expected return and the same variance of return
or (b) a lower variance of return and the same expected return.”
Natomiast dokładnie tak jak w Definicji 7.2 (i to od samego
początku!) proponował rozumieć efektywność Markowitz w [19].
Pisał on tam na stronie 82: ”The ![]() –
– ![]() rule states that the
investor would (or should) want to select one of those portfolios
which give rise to the
rule states that the
investor would (or should) want to select one of those portfolios
which give rise to the ![]() combinations indicated as efficient
in the figure; i. e., those with minimum
combinations indicated as efficient
in the figure; i. e., those with minimum ![]() for given
for given ![]() or more and maximum
or more and maximum ![]() for given
for given ![]() or less.”
or less.”
Czytelnik zechce zauważyć, że to `and' w cytacie z HMM jest
koniunkcją logiczną!! (Dokonane tu wytłuszczenia nie
pochodzą od autora pracy [19].) Istotnie, pierwsza część
tej koniunkcji wyklucza hipotetyczne portfele, których
obrazy leżałyby względem punktu ![]() [nasz porządek zmiennych,
nie ten egzotyczny ulubiony przez HMM!!] w:
[nasz porządek zmiennych,
nie ten egzotyczny ulubiony przez HMM!!] w: ![]() kątowniku północno-zachodnim
z wąsem poziomo w lewo od
kątowniku północno-zachodnim
z wąsem poziomo w lewo od ![]() , lecz bez wąsa
pionowo w górę od
, lecz bez wąsa
pionowo w górę od ![]() . Natomiast druga część koniunkcji
wyklucza portfele, których obrazy leżałyby w:
. Natomiast druga część koniunkcji
wyklucza portfele, których obrazy leżałyby w: ![]() tymże
kątowniku północno-zachodnim z wąsem pionowo w górę, lecz
bez wąsa poziomo w lewo
tymże
kątowniku północno-zachodnim z wąsem pionowo w górę, lecz
bez wąsa poziomo w lewo ![]() . Łącznie koniunkcja wyklucza
więc portfele, których obrazy leżałyby w całym domkniętym kątowniku
północno-zachodnim bez samego wierzchołka kątownika
. Łącznie koniunkcja wyklucza
więc portfele, których obrazy leżałyby w całym domkniętym kątowniku
północno-zachodnim bez samego wierzchołka kątownika ![]() , czyli
te, które dominowałyby w naszym sensie [Definicja 7.1] dany
portfel i przy tym miały różny od niego obraz na płaszczyźnie
wariancja – wartość oczekiwana — patrz (też) interpretacja
geometryczna zaraz po Definicji 7.2 powyżej.
, czyli
te, które dominowałyby w naszym sensie [Definicja 7.1] dany
portfel i przy tym miały różny od niego obraz na płaszczyźnie
wariancja – wartość oczekiwana — patrz (też) interpretacja
geometryczna zaraz po Definicji 7.2 powyżej.
Dla wygody czytelnika (prawie) całą przywoływaną tu stronę z [19] reprodukujemy na Rysunku 7.2 poniżej. [W wersji pdf rysunek przeskoczył na następną stronę.]
W książce [22] – wydanie późniejsze od [19] o 48
lat – autor, na pewno dydaktycznie przejrzyściej (lecz cały czas dokładnie
o tym samym!) mówi w Definicji na stronie 6, które punkty w jego mapie
![]() są nieefektywne:
są nieefektywne:
”An obtainable ![]() combination is inefficient if another
obtainable combination has either higher mean and no higher variance,
or less variance and no less mean. [And] efficient are
those which are not inefficient.”
combination is inefficient if another
obtainable combination has either higher mean and no higher variance,
or less variance and no less mean. [And] efficient are
those which are not inefficient.”
Przykład 7.2
Granicą efektywną ![]() w przykładzie Krzyżewskiego
(aspekt oczywiście M) jest cała granica minimalna:
w przykładzie Krzyżewskiego
(aspekt oczywiście M) jest cała granica minimalna:
![]() .
.
Istotnie, policzmy wysokości na osi ![]() czubków gałęzi hiperbol – obrazów, korzystając z obliczeń
w Wykładach: V (dla boków) i VI (dla prostej krytycznej;
jej obraz to – jak wiemy – pocisk Markowitza).
czubków gałęzi hiperbol – obrazów, korzystając z obliczeń
w Wykładach: V (dla boków) i VI (dla prostej krytycznej;
jej obraz to – jak wiemy – pocisk Markowitza).
| Dla boku |
|
poniżej aktywnego obszaru |
|---|---|---|
| dla boku |
|
poniżej aktywnego obszaru |
| dla boku |
|
poniżej aktywnego obszaru |
| dla prostej krytycznej: |
|
poniżej aktywnego obszaru |
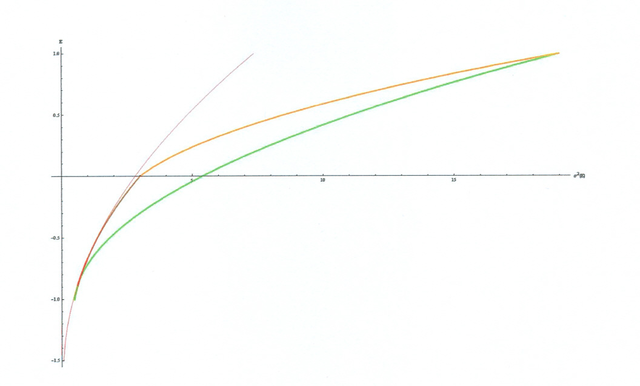
Istotnie więc, wszystkie cztery łuki hiperbol tworzących
![]() leżą w górnych połowach odpowiednich
gałęzi hiperbol. Te łuki są zatem zbudowane z
leżą w górnych połowach odpowiednich
gałęzi hiperbol. Te łuki są zatem zbudowane z
![]() –obrazów portfeli efektywnych.
–obrazów portfeli efektywnych.
Zauważmy przy okazji, że wysokość czubka samego
pocisku Markowitza, owe ![]() , pojawiła się
już w Uwadze 6.2 w Wykładzie VI; wtedy jako zwiastun
niebezpieczeństw związanych z modelowaniem Blacka.
, pojawiła się
już w Uwadze 6.2 w Wykładzie VI; wtedy jako zwiastun
niebezpieczeństw związanych z modelowaniem Blacka.
Na Rysunku 7.3 jest widoczna jeszcze jedna rzecz godna uwagi:
granica minimalna ma punkt załamania na wysokości ![]() .
.
Ćwiczenie 7.1
Używając wzorów obrazów boków w tym przykładzie (podanych na
początku Wykładu V), policzyć kąt załamania granicy minimalnej
w aspekcie M, na Rysunku 7.3 na wysokości ![]() .
.
Należy obliczyć kąt, pod jakim przecinają się przy ![]() łuki dwu parabol (tak, parabol!) o znanych wzorach. Ten kąt ma miarę
łuki dwu parabol (tak, parabol!) o znanych wzorach. Ten kąt ma miarę
![]() ,
czyli około
,
czyli około ![]() .
.
(Oba rysunki reprodukowane tu powyżej pochodzą z pracy magisterskiej [8], która jest jeszcze raz cytowana niżej w bieżącym Wykładzie VII.)
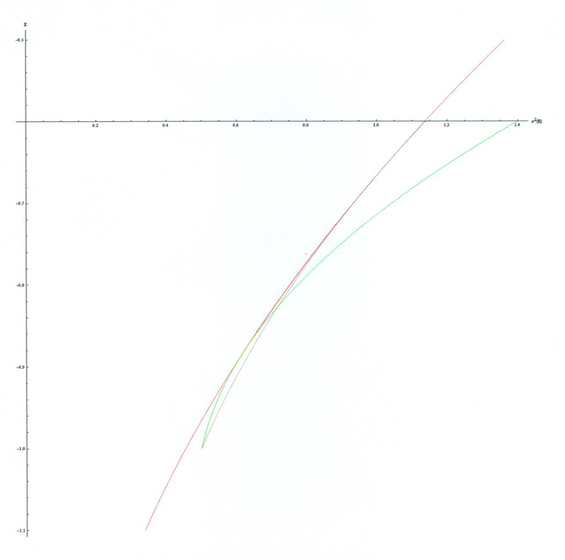
Ćwiczenie 7.2
Co na Rysunku 7.4 narysowane jest jednak nie w 100![]() idealnie?
idealnie?
Skoro wiemy już, że w przykładzie Krzyżewskiego w aspekcie M cała granica minimalna (a więc: w obrazie) jest efektywna, zobaczmy, jak w nim wygląda cały zbiór portfeli efektywnych (a więc: w źródle). [W wersji pdf Rysunek 7.5 idzie dopiero dwie strony dalej.]
Zbiór ten jest więc już dosyć skomplikowany. Byłoby dobrze go zapamiętać; hasło na przyszłość – łamana efektywna, jak w podpisie pod tym rysunkiem.15ścisłe jej określenie to dopiero Definicja 11.1 w Wykładzie XI Ta przyszłość to konkretnie Wykłady: X (z Twierdzeniem 10.1 o łamanej wierzchołkowej) oraz XI (z dowodem tegoż i z dyskusją łamanych efektywnych).
Z kolei, nauczeni Przykładem 7.1, zadajemy sobie pytanie, jaki – w tym samym przykładzie Krzyżewskiego – jest zbiór portfeli efektywnych przy zmianie aspektu z M na B? I oto odpowiedź. [W wersji pdf ta odpowiedź – Rysunek 7.6 – trafia na następną stronę.]
Jest więc z grubsza tak, jak w Przykładzie 7.1 – zbiory portfeli efektywnych w danych aspektach różnią się zasadniczo. Czy zapamiętamy i to rozróżnienie?
Ćwiczenie 7.3
Znaleźć wszystkie portfele efektywne w aspekcie M
w modelu z Przykładu 5.2 (Wykład V) przy ![]() :
:
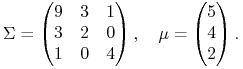 |
Korzystamy bardzo mocno z Rysunku 5.3 w Wykładzie V. Dzięki temu widzimy,
że do odpowiedzi (czyli do łamanej efektywnej) na pewno wchodzi cały bok
![]() . Ponadto – jeszcze jakiś przedział leżący w boku
. Ponadto – jeszcze jakiś przedział leżący w boku
![]() . Jaki?
. Jaki?
Rozwijając myśl ze wskazówki, musimy znaleźć na boku ![]() portfel przechodzący na dzióbek hiperboli – obrazu prostej tego boku.
Od takiego portfela zaczynać się tu będzie łamana efektywna.
W tym celu wystarczy np policzyć lokalne dla tego boku parametry
portfel przechodzący na dzióbek hiperboli – obrazu prostej tego boku.
Od takiego portfela zaczynać się tu będzie łamana efektywna.
W tym celu wystarczy np policzyć lokalne dla tego boku parametry
![]() i
i ![]() . Macierz kowariancji dla walorów numer 2 i 3 jest
diagonalna i niemal natychmiast dostajemy
. Macierz kowariancji dla walorów numer 2 i 3 jest
diagonalna i niemal natychmiast dostajemy ![]() oraz
oraz
![]() . Dzióbek jest zatem na wysokości
. Dzióbek jest zatem na wysokości
![]() , a więc jest to
, a więc jest to
![]() –obraz portfela
–obraz portfela ![]() .
Tym sposobem wiemy już, że brakująca część łamanej efektywnej to odcinek
domknięty od napisanego tu portfela do portfela
.
Tym sposobem wiemy już, że brakująca część łamanej efektywnej to odcinek
domknięty od napisanego tu portfela do portfela ![]() . (Łamana efektywna
składa się tu z dwóch boków.)
. (Łamana efektywna
składa się tu z dwóch boków.)
Ćwiczenie 7.4 (kontynuacja ćwiczenia z Uwagi 7.2 powyżej)
a) Znaleźć wszystkie portfele efektywne w aspekcie M
w przykładzie (7.1). Następnie narysować je na wybranym
rzucie 2-wymiarowym sympleksu ![]() .
.
b) Znaleźć wszystkie portfele efektywne w aspekcie B
w przykładzie (7.1). Następnie narysować je na wybranym
rzucie 2-wymiarowym płaszczyzny ![]() .
.
Praktycznie wszystko, co niezbędne, zostało już powiedziane w Uwadze 7.2.
Garść informacji historycznych dotyczących granic
![]() i
i ![]() w aspekcie M.
w aspekcie M.
W przyszłości poznamy naturalne ograniczenie górne ![]() na ilość kawałków
na ilość kawałków ![]() , z jakich składa się granica
, z jakich składa się granica ![]() w niezdegenerowanym modelu Markowitza w wymiarze
w niezdegenerowanym modelu Markowitza w wymiarze ![]() . Z Obserwacji 7.1
wynika, że takie samo jest/będzie ograniczenie na ilość kawałków
. Z Obserwacji 7.1
wynika, że takie samo jest/będzie ograniczenie na ilość kawałków
![]() , z jakich składa się granica
, z jakich składa się granica ![]() :
:
-
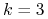 : przykład Krzyżewskiego pokazuje, że możliwa
jest ”
: przykład Krzyżewskiego pokazuje, że możliwa
jest ”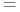 ” w obu tych oszacowaniach, i to realizowana na tym
samym przykładzie!
” w obu tych oszacowaniach, i to realizowana na tym
samym przykładzie!
-
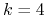 : były student Wydziału MIM UW, K. Więch podał
w roku 2001 w [29] przykład (10.7), w którym
osiągana jest równość w pierwszym oszacowaniu, zaś w drugim po
lewej stronie stoi
: były student Wydziału MIM UW, K. Więch podał
w roku 2001 w [29] przykład (10.7), w którym
osiągana jest równość w pierwszym oszacowaniu, zaś w drugim po
lewej stronie stoi 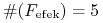 . (Jeszcze w wersji
z roku 2000 wykładów [13] było to pytaniem otwartym, czy
przy
. (Jeszcze w wersji
z roku 2000 wykładów [13] było to pytaniem otwartym, czy
przy 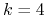 w pierwszym oszacowaniu możliwa jest równość.)
w pierwszym oszacowaniu możliwa jest równość.)
Ten wynik poprawił w roku 2007 inny student MIM UW A. Iwanicki, uzyskując w [9] przykład, w którym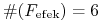 .
Jego z kolei prześcignęli jeszcze inni studenci MIM-u P. Grodzki
i J. Gruszczyński, którzy w 2008 w [8] podali dwa
niezmiernie interesujące przykłady. W pierwszym z nich
.
Jego z kolei prześcignęli jeszcze inni studenci MIM-u P. Grodzki
i J. Gruszczyński, którzy w 2008 w [8] podali dwa
niezmiernie interesujące przykłady. W pierwszym z nich
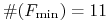 ,
, 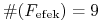 .
W drugim natomiast
.
W drugim natomiast 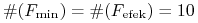 .
Ten drugi jest przy tym tak estetyczny, że nie można go nie
przytoczyć w tych wykładach:
.
Ten drugi jest przy tym tak estetyczny, że nie można go nie
przytoczyć w tych wykładach: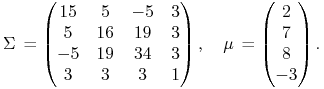
-
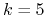 : A. Iwanicki podał, także w [9],
przykład, w którym osiągana jest ”
: A. Iwanicki podał, także w [9],
przykład, w którym osiągana jest ”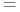 ” w pierwszym oszacowaniu,
” w pierwszym oszacowaniu,
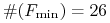 (
(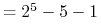 ). Ten przykład jest
przytoczony i dyskutowany w ostatnim Wykładzie XV.
). Ten przykład jest
przytoczony i dyskutowany w ostatnim Wykładzie XV.
-
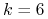 : Ten sam Iwanicki znalazł pod koniec roku 2007
(już po obronieniu licencjatu) przykład, w którym także osiągana
jest ”
: Ten sam Iwanicki znalazł pod koniec roku 2007
(już po obronieniu licencjatu) przykład, w którym także osiągana
jest ”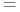 ” w pierwszym oszacowaniu
” w pierwszym oszacowaniu 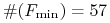 (
(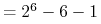 ).
).
Te rezultaty w naturalny sposób prowadzą do postawienia ważnego pytania.
Ćwiczenie 7.5 (otwarte)
Czy w wymiarze 4 możliwe jest, by ![]() ?
?