8. Wykład VIII, 20.XI.2009

Na tym wykładzie zaczniemy poznawać teorię Jamesa Tobina – również, jak i Markowitz, laureata nagrody Nobla z ekonomii (nawet wcześniejszego, bo już z roku 1981), który wzbogacił modelowanie inwestowania – i osiągania zysków na giełdzie! – o możliwość zaciągania pożyczek i/lub lokowania części środków w banku oferującym, bez żadnego ryzyka, stałą stopę zwrotu $\mu _{0}$ w zadanym okresie inwestycyjnym.¹⁶Tobin jest również znany, może nawet bardziej, z idei wprowadzenia czegoś w rodzaju firewallu chroniącego przed kryzysami spekulacyjnymi – tzw. podatku Tobina od wszelkich operacji finansowych, którą to ideę głosił od bardzo dawna, jednak zawsze z miernymi efektami praktycznymi. Niejeden raz okrzykiwano go, właśnie w związku z tym pomysłem, ,,lewakiem”. Jego idea odżyła na nowo w trakcie kryzysu lat 2008-9.

Oryginalnie Tobin wzbogacił w ten sposób teorię Markowitza (dla przypomnienia – dopuszczalne są w niej tylko długie pozycje w inwestycjach giełdowych). Modelem Tobina sensu stricto zajmiemy się w przyszłości. Pojęciowo i też matematycznie prostsze jest wzbogacenie, o pożyczki i/lub lokaty w banku, modelu Blacka (dla przypomnienia – dopuszczalne są w nim także krótkie pozycje, i to w nieograniczonej wysokości).

Jest to zmodyfikowany model Tobina, w żargonie matematyki finansowej nazywany też czasami krótko ,,Black z dodanym walorem bezryzykownym $\mu _{0}$ ”. Należy podkreślić wyidealizowany charakter również tego modelowania: pożyczki i lokaty w banku są oprocentowane dokładnie tak samo, przy czym – one także! – możliwe są w nieograniczonej wysokości.

Pamiętamy wzór bilansowy (5.3) (Wykład V) leżący u podstaw krótkiej i długiej sprzedaży w teorii Blacka. Obecnie inwestor może dodatkowo pożyczyć dowolną ilość $A_{0}$ środków w banku, oprocentowanych $\mu _{0}$ w okresie inwestycyjnym. Jeśli tak postąpi, to jego poprzedni bilans (5.3) przybierze postać

$L+\sum _{{j\in J}}A_{j}+A_{0}=\sum _{{i\in I}}A_{i}\,.$

(8.1)

Środki własne inwestora $L$ i uzyskane z krótkich sprzedaży $\sum _{{j\in J}}A_{j}$ zostają tu jeszcze powiększone o pożyczone w banku $A_{0}$ , po czym sumę tych wszystkich środków inwestor przeznacza na zwyczajny zakup akcji o numerach $i\in I$ .

Gdy natomiast inwestor deponuje część już posiadanych środków, np wielkość $A_{0}$ (zależną wprawdzie od jego kapitału wyjściowego oraz od już poczynionych krótkich sprzedaży akcji, jednak wobec dowolności tych drugich – w praktyce nieograniczoną), we wspomnianym banku, wtedy bilans (5.3) zamienia się na

$L+\sum _{{j\in J}}A_{j}=A_{0}+\sum _{{i\in I}}A_{i}\,.$

(8.2)

Zwyczajne zakupy inwestora składają się teraz z ,,zakupu” bezryzykownego i bezpiecznego zysku o stopie $\mu _{0}$ za kwotę $A_{0}$ oraz z zakupów akcji spółek o numerach $i\in I$ za kwoty $A_{i}$ .

W przypadku pożyczki w banku, bilans (8.1) zapisujemy w postaci

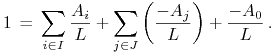$1\,=\,\sum _{{i\in I}}\frac{A_{i}}{L}+\sum _{{j\in J}}\left(\frac{-A_{j}}{L}\right)+\frac{-A_{0}}{L}\,.$

(8.3)

Natomiast w przypadku depozytu w banku, bilans (8.2) zapisujemy w postaci

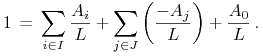$1\,=\,\sum _{{i\in I}}\frac{A_{i}}{L}+\sum _{{j\in J}}\left(\frac{-A_{j}}{L}\right)+\frac{A_{0}}{L}\,.$

(8.4)

W zmodyfikowanym modelu Tobina portfel inwestora zostaje zatem zakodowany w postaci dodatnich liczb $x_{i}=\frac{A_{i}}{L}$ ( $i\in I$ , długie pozycje), ujemnych liczb $x_{j}=\frac{-A_{j}}{L}$ ( $j\in J$ , krótkie pozycje), ewentualnych zer na miejscach spółek, którymi inwestor w ogóle się nie zainteresował, oraz dodatkowej współrzędnej

$x_{0}=\begin{cases}\frac{-A_{0}}{L}&\text{gdy zaciąga pożyczkę $A_{0}$ w banku}\\ \frac{A_{0}}{L}&\text{gdy deponuje kwotę $A_{0}$ w banku}\end{cases}$

opisującej jego postępowanie względem banku. Wszystkie te współrzędne, niezależnie od znaku współrzędnej $x_{0}$ , zawsze sumują się do 1, jak to widzimy w (8.3) i (8.4).

Wartości oczekiwane portfeli w tym modelu, o ile tylko nie wszystkie parametry $\mu _{0},\,\mu _{1},\dots,\,\mu _{k}$ są sobie równe (co oczywiście zakładamy, patrz Twierdzenie 8.1 poniżej), są – analogicznie jak w Blacku, Uwaga 6.2 w Wykładzie VI – nieograniczone z obu stron. A więc również z dołu; nie ma jakiejś ,,naturalnej” granicy $-1$ od dołu dla stopy straty. Można tu, średnio biorąc, dowolnie dużo relatywnie zyskać, lecz można też dowolnie dużo relatywnie stracić!

Ćwiczenie 8.1 (pytanie kontrolne)

Inwestor wkracza do Domu Maklerskiego ze swoimi 3000. Krótko sprzedaje akcje pewnej spółki za 18 tysięcy, po czym pożycza jeszcze w banku 11 tysięcy. Następnie kupuje akcje dwu innych spółek w proporcji wartościowej 3:1. Jaki jest jego portfel $\widetilde{x}$ ?

Rozwiązanie:

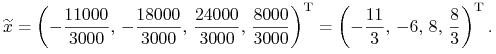$\widetilde{x}=\left(-\frac{11000}{3000},\,-\frac{18000}{3000},\,\frac{24000}{3000},\,\frac{8000}{3000}\right)^{{\text{T}}}=\left(-\frac{11}{3},\,-6,\, 8,\,\frac{8}{3}\right)^{{\text{T}}}.$

Po tym wprowadzeniu, teraz już formalnie:

zmodyfikowany model Tobina, budowany nad modelem Blacka $k\times k$ z parametrami $\Sigma>0$ i $\mu\nparallel e$ , jest to pewien inny model Blacka $(k+1)\times(k+1)$ z macierzą kowariancji wymiaru $k+1$

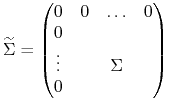$\widetilde{\Sigma}=\begin{pmatrix}0&0&\dots&0\\ 0&&&\\ \vdots&&\Sigma&\\ 0&&&\end{pmatrix}$

(8.5)

(inwestowanie w bankowy walor bezryzykowny ma zerową wariancję stopy zwrotu i jest nieskorelowane ze zwrotami z akcji spółek giełdowych – ryzykownych) oraz wektorem stóp zwrotu

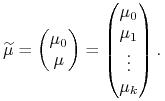$\widetilde{\mu}=\begin{pmatrix}\mu _{0}\\ \mu\end{pmatrix}=\begin{pmatrix}\mu _{0}\\ \mu _{1}\\ \vdots\\ \mu _{k}\end{pmatrix}.$

Portfele w tym modelu to wszystkie punkty z hiperpłaszczyzny $\widetilde{H}\subset\mathbb{R}^{{k+1}}$ opisanej równaniem $x_{0}+x_{1}+\cdots+x_{k}=1$ , będącym tylko inną postacią równań (8.3) i (8.4).

W celu uniknięcia kolizji oznaczeń z teorią Blacka, będziemy zapisywać te portfele jako

$\widetilde{H}\ni\widetilde{x}=\begin{pmatrix}x_{0}\\ z\end{pmatrix},$

gdzie $z\in\mathbb{R}^{k}$ .

Wartość oczekiwaną $E(\widetilde{x})$ portfela $\widetilde{x}$ w tej nowej teorii liczymy zupełnie analogicznie do tego, jak robiliśmy to w Wykładzie VI dla portfeli Blacka, zważając tylko no to, że dla waloru bezryzykownego nie mamy jego cen: początkowej i końcowej $C_{{0,\text{pocz}}}$ i $C_{{0,\text{kon}}}$ , z których powstawałaby stopa zwrotu $R_{0}$ , tylko po prostu zmienna losowa $R_{0}$ jest stałą: $R_{0}=\mu _{0}$ .
Jeśli inwestor składa w banku na początku depozyt $A_{0}$ , wtedy na końcu odbiera $(1+\mu _{0})A_{0}$ , co w stosunku do jego kapitału własnego $L$ daje stopę zysku $\mu _{0}\frac{A_{0}}{L}=\mu _{0}x_{0}$ .
Jeśli natomiast na początku bierze on w banku pożyczkę $A_{0}$ , to na końcu musi oddać $(1+\mu _{0})A_{0}$ , co daje ujemną stopę zysku $-\mu _{0}\frac{A_{0}}{L}=\mu _{0}x_{0}$ .

Klasyczny wzór na stopę zwrotu z portfela rozszerza się zatem z ,,Blacka” do ,,zmodyfikowanego Tobina” i mamy tutaj $E(\widetilde{x})=\widetilde{\mu}^{{\text{T}}}\widetilde{x}$ , jak również, oczywiście, $\sigma^{2}(\widetilde{x})=\sigma^{2}(z)=z^{{\text{T}}}\Sigma\, z$ (por. (8.5)).

W tym momencie znamy już odwzorowanie Markowitza w zmodyfikowanym modelu Tobina! Teraz podstawowe pytanie teorii to – jak już było w Blacku i jak będzie w przyszłości z powrotem w Markowitzu – pytanie o postać (kształt) granicy minimalnej.

Twierdzenie 8.1

Zakładamy, że w wyjściowym modelu Blacka macierz kowariancji $\Sigma$ jest dodatnio określona oraz spełnione jest fundamentalne założenie (5.2) z Wykładu V. O stopie zwrotu w banku $\mu _{0}$ zakładamy tylko, że $\mu _{0}>-1$ (tj, że w banku nie stracimy wszystkiego). Wtedy

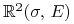(i) granica minimalna w zmodyfikowanym modelu Tobina to kątownik złożony z dwu półprostych na płaszczyźnie $\mathbb{R}^{2}(\sigma,\, E)$ ,

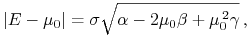
$|E-\mu _{0}|=\sigma\sqrt{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}\,,$

gdzie wyrażenie pod pierwiastkiem jest dodatnie, będąc (również) liczbą 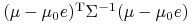$(\mu-\mu _{0}e)^{{\text{T}}}\Sigma^{{-1}}(\mu-\mu _{0}e)$ , czyli wartością dodatnio określonej formy kwadratowej na niezerowym wektorze. W kątowniku tym automatycznie 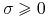$\sigma\ge 0$ . Ten kątownik jest czasem nazywany krótko kątownikiem Tobina (lecz patrz też Figure IV w pracy [23]).
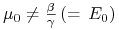(ii) Jeśli $\mu _{0}\ne\frac{\beta}{\gamma}\,(=\, E_{0})$ , to kąt rozwarcia kątownika opisanego w (i) jest większy od kąta rozwarcia kątownika asymptot w wyjściowym modelu Blacka:

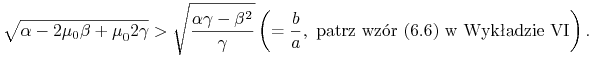
$\sqrt{\alpha-2\mu _{0}\beta+\mu _{0}^{{\,}}2\gamma}>\sqrt{\frac{\alpha\gamma-\beta^{2}}{\gamma}}\left(=\frac{b}{a},\ \text{patrz wzór (6.6) w Wykładzie VI}\right).$
(iii) Jeśli 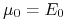$\mu _{0}=E_{0}$ , to kątownik Tobina pokrywa się z kątownikiem asymptot pocisku Markowitza w wyjściowym modelu Blacka.

Dowód, z dokładnością do innych oznaczeń, bazuje na pracy [23].

Dowód (i). Zgodnie z definicją granicy minimalnej, przy dowolnej ustalonej wartości $\widetilde{E}\in\mathbb{R}$ minimalizujemy funkcję $\frac{1}{2}\sigma^{2}(\widetilde{x})=\frac{1}{2}\sigma^{2}(z)$ na hiperpłaszczyźnie $\widetilde{H}$ . Zatem – minimalizujemy funkcję $\frac{1}{2}z^{{\text{T}}}\Sigma\, z$ , gdzie $z\in\mathbb{R}^{k}$ (!), przy ograniczeniach

$\left\{\begin{array}[]{ll}\mu^{{\text{T}}}z+\mu _{0}x_{0}&=\widetilde{E},\\ e^{{\text{T}}}z+x_{0}&=1.\end{array}\right.$

Jeszcze przed napisaniem warunku Lagrange'a ograniczenia te upraszczamy, eliminując zmienną $x_{0}$ . Dostajemy wtedy już tylko jeden warunek $\mu^{{\text{T}}}z+\mu _{0}(1-e^{{\text{T}}}z)=\widetilde{E}$ , albo

$(\mu-\mu _{0}e)^{{\text{T}}}z=\widetilde{E}-\mu _{0}\,.$

(8.6)

Rozwiązaniem będzie $\widetilde{x}=\left(\begin{smallmatrix}1-e^{{\text{T}}}z\\ z\end{smallmatrix}\right)$ taki, że $\Sigma z=\lambda(\mu-\mu _{0}e)$ dla jakiegoś $\lambda\in\mathbb{R}$ . Okaże się bowiem, że taki $\lambda$ będzie jedyny, więc $z$ będzie jedynym kandydatem na lokalne ekstremum warunkowe. W rozważanej sytuacji, przy ścisłej wypukłości wariancji w zakresie zmiennych od $x_{1}$ do $x_{k}$ , $z$ będzie globalnym minimum warunkowym (porównaj analogiczną sytuację i Ćwiczenie 6.4 w Wykładzie VI).
Istotnie, wyrażenie na $z$ ,

$z=\lambda\Sigma^{{-1}}(\mu-\mu _{0}e),$

(8.7)

można wstawić do (8.6), dostając

$(\mu-\mu _{0}e)^{{\text{T}}}\lambda\Sigma^{{-1}}(\mu-\mu _{0}e)=\widetilde{E}-\mu _{0},$

albo

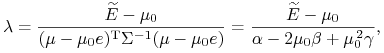$\lambda=\frac{\widetilde{E}-\mu _{0}}{(\mu-\mu _{0}e)^{{\text{T}}}\Sigma^{{-1}}(\mu-\mu _{0}e)}=\frac{\widetilde{E}-\mu _{0}}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma},$

gdzie wielkość w mianowniku jest dodatnia, bo jest to wartość formy kwadratowej o macierzy $\Sigma^{{-1}}$ na niezerowym wektorze $\mu-\mu _{0}e$ (litery greckie $\alpha$ , $\beta$ , $\gamma$ zostały zdefiniowane w Wykładzie VI). Właśnie to wyrażenie na $\lambda$ podstawione do (8.7) daje jednoznaczny wzór na $z=z(\widetilde{E})$ ,

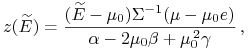$z(\widetilde{E})=\frac{(\widetilde{E}-\mu _{0})\Sigma^{{-1}}(\mu-\mu _{0}e)}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}\,,$

czyli – należy zauważyć – wzór (36) w [23]. To poprzez warunek budżetowy daje

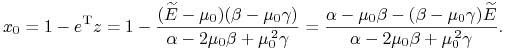$x_{0}=1-e^{{\text{T}}}z=1-\frac{(\widetilde{E}-\mu _{0})(\beta-\mu _{0}\gamma)}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}=\frac{\alpha-\mu _{0}\beta-(\beta-\mu _{0}\gamma)\widetilde{E}}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}.$

Mamy już w tej chwili cały portfel Tobina $\widetilde{x}(\widetilde{E})$ minimalizujący ryzyko na każdym ustalonym poziomie wartości oczekiwanej $\widetilde{E}$ :

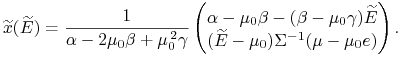$\widetilde{x}(\widetilde{E})=\frac{1}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}\begin{pmatrix}\alpha-\mu _{0}\beta-(\beta-\mu _{0}\gamma)\widetilde{E}\\ (\widetilde{E}-\mu _{0})\Sigma^{{-1}}(\mu-\mu _{0}e)\end{pmatrix}.$

(8.8)

Portfele te, gdy $\widetilde{E}$ przebiega $\mathbb{R}$ , tworzą prostą w hiperpłaszczyźnie $\widetilde{H}\in\mathbb{R}^{{k+1}}$ . Jest to prosta krytyczna w tym zagadnieniu, zwana prostą krytyczną Tobina.¹⁷zwracamy uwagę na ten kapitalny fakt: nic więcej, tylko prosta, mimo, że model jest częściowo zdegenerowany; ciekawe

Liczymy teraz wartość znalezionego relatywnego minimum wariancji portfela na poziomie $\widetilde{E}$ , tzn. wielkość $\sigma^{2}(\widetilde{x}(\widetilde{E}))=:\sigma^{2}(\widetilde{E})$ , opuszczając już dalej falkę nad $E$ :

$\sigma^{2}(E)=\frac{(E-\mu _{0})^{2}}{(\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma)^{2}}\big(\mu^{{\text{T}}}-\mu _{0}e^{{\text{T}}}\big)\Sigma^{{-1}}\Sigma\,\Sigma^{{-1}}(\mu-\mu _{0}e)\\ =\frac{(E-\mu _{0})^{2}}{(\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma)^{2}}(\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma)=\frac{(E-\mu _{0})^{2}}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma},$

albo, pisząc tylko $\sigma$ zamiast $\sigma(E)$ ,

$|E-\mu _{0}|=\sigma\sqrt{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}.$

Dowód części (i) jest zakończony.

Dowód (ii). Pokażemy, że kwadraty porównywanych tangensów połówek kątów rozwarcia kątowników spełniają nierówność

$\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma>\frac{\alpha\gamma-\beta^{2}}{\gamma}.$

(8.9)

Rozpatrujemy w tym celu trójmian kwadratowy

$\mathbb{R}\ni\lambda\longmapsto(\mu^{{\text{T}}}-\lambda e^{{\text{T}}})\Sigma^{{-1}}(\mu-\lambda e)\in\mathbb{R}\,,$

który jest wszędzie dodatni, więc ma ujemny wyróżnik.¹⁸Jest to trójmian $\alpha-2\beta\lambda+\gamma\lambda^{2}$ ; dla niego $\frac{1}{4}\Delta=\beta^{2}-\alpha\gamma$ . To, przy okazji, już trzeci dowód podstawowego w teorii Blacka Lematu 6.1 z Wykładu VI: $\alpha\gamma-\beta^{2}>0$ . Przyjmuje on minimum w $\lambda=\frac{\beta}{\gamma}$ . To znaczy, że jego wartość w $\lambda=\frac{\beta}{\gamma}\ne\mu _{0}$ , tzn. liczba

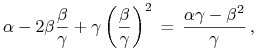$\alpha-2\beta\frac{\beta}{\gamma}+\gamma\left(\frac{\beta}{\gamma}\right)^{2}\,=\,\frac{\alpha\gamma-\beta^{2}}{\gamma}\,,$

jest mniejsza niż wartość w $\lambda=\mu _{0}$ , tzn. mniejsza niż liczba $\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma$ . Nierówność (8.9) została udowodniona, a wraz z nią część (ii) twierdzenia.

Równocześnie udowodniliśmy też część (iii): przy $\mu _{0}=E_{0}$ równe są i tangensy kątów, i punkty na pionowej osi, w których kątownik Tobina oraz kątownik asymptot pocisku dotykają tej osi.

∎

Twierdzenie 8.1 jest udowodnione. Analizując kątownik Tobina wyłaniający się z części (i) w tym twierdzeniu, nasuwa się jednak następująca

Uwaga 8.1

Czytelnik może poczuć się lekko zdezorientowany. Tutaj częściowo zdegenerowana macierz $\widetilde{\Sigma}$ powoduje, że granica minimalna nie jest już regularnym pociskiem [Markowitza], tylko degeneruje się do kątownika z wierzchołkiem na osi $\overrightarrow{OE}$ . Mówiąc po prostu, w zmodyfikowanym Tobinie ryzyko można zredukować do zera.

Tymczasem tamten dziwny przykład analizowany szczegółowo w Uwadze 7.2 w Wykładzie VII pokazywał coś przeciwnego! Częściowo zdegenerowana macierz kowariancji $\Sigma$ i jednak regularny pocisk Markowitza w granicy minimalnej.

Wyjaśnienie jest takie. Tam forma dawana macierzą $\Sigma$ nie degenerowała się na wektorach z [hiper]płaszczyzny $H$ , kres dolny jej wartości na nich był 1. Natomiast teraz forma dawana macierzą $\widetilde{\Sigma}$ zeruje się na wektorze $(1,\, 0,\dots,\, 0)^{{\text{T}}}\in\widetilde{H}$ (i, zresztą, w ramach $\widetilde{H}$ tylko na nim).

Uwaga 8.2

W teorii zmodyfikowanego modelu Tobina zakłada się, że $\mu _{0}<\frac{\beta}{\gamma}$ ( $=E_{0}$ ), co będzie później obszernie komentowane w Wykładzie IX. To pociąga $\beta-\mu _{0}\gamma>0$ , więc – w szczególności – składowa $x_{0}$ portfela (8.8) na prostej Tobina może być sprowadzona do zera.

Przyjrzyjmy się teraz dokładniej prostej Tobina w sytuacji ogólniejszej niż w Uwadze 8.2, gdy $\mu _{0}\ne E_{0}$ , tzn. $\beta-\mu _{0}\gamma\ne 0$ . Wtedy też można wyzerować składową $x_{0}$ w portfelu Tobina (8.8). I łatwo jest wskazać dwa charakterystyczne punkty, przez które przechodzi prosta Tobina. Są to na przykład

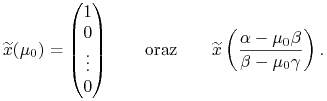$\widetilde{x}(\mu _{0})=\begin{pmatrix}1\\ 0\\ \vdots\\ 0\\ \end{pmatrix}\qquad\text{oraz}\qquad\widetilde{x}\left(\frac{\alpha-\mu _{0}\beta}{\beta-\mu _{0}\gamma}\right).$

Ten drugi to właśnie ten punkt na prostej Tobina, który ma zerową składową numer 0 — zaraz okaże się on portfelem tkwiącym jakby jeszcze w teorii Blacka i nierobiącym użytku z banku oferującego walor bezryzykowny. (Te dwa charakterystyczne punkty są zaznaczone na czerwono na Rysunku 9.1 w Wykładzie IX. Z pewnego względu rysunek nie pojawia się tu i teraz, lecz dopiero tam.¹⁹jednak odległość ,,portalowa” jest niewielka)

Przyjrzyjmy się dokładniej temu punktowi, zapominając o jego współrzędnej $x_{0}=0$ , tzn. biorąc tylko jego część $z$ w terminologii z dowodu Twierdzenia 8.1 powyżej.

Ćwiczenie 8.2 (Pytanie kontrolne)

Czy punkt $z\left(\frac{\alpha-\mu _{0}\beta}{\beta-\mu _{0}\gamma}\right)$ leży w hiperpłaszczyźnie $H\subset\mathbb{R}^{k}$ , tzn. czy jest on portfelem Blacka?

Rozwiązanie:

Tak, oczywiście, z warunku budżetowego spełnionego tożsamościowo na prostej Tobina, bo wtedy $x_{0}=0$ .

Policzmy ten punkt-portfel dokładniej,

$z\left(\frac{\alpha-\mu _{0}\beta}{\beta-\mu _{0}\gamma}\right)\,=\,\frac{1}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}\left(\frac{\alpha-\mu _{0}\beta}{\beta-\mu _{0}\gamma}-\mu _{0}\right)\Sigma^{{-1}}(\mu-\mu _{0}e)\,=\,\frac{\Sigma^{{-1}}(\mu-\mu _{0}e)}{\beta-\mu _{0}\gamma}\,,$

(8.10)

bo to jedna z najważniejszych formuł w analizie portfelowej, warta zapamiętania na dłużej. Mówiąc nawiasowo, przy jej pomocy sprawdzenie warunku budżetowego jest wdzięczne, choć – po Ćwiczeniu 8.2 – nadmiarowe:

$e^{{\text{T}}}z\left(\frac{\alpha-\mu _{0}\beta}{\beta-\mu _{0}\gamma}\right)=\frac{1}{\beta-\mu _{0}\gamma}e^{{\text{T}}}\Sigma^{{-1}}(\mu-\mu _{0}e)=\frac{\beta-\mu _{0}\gamma}{\beta-\mu _{0}\gamma}\,=\, 1\,.$

Na koniec tego wykładu jeszcze kilka zdań na temat specjalnej sytuacji, osobno wybitej jako (iii) w Twierdzeniu 8.1. Gdy $\mu _{0}=\frac{\beta}{\gamma}$ , wtedy składowej $x_{0}$ w portfelu Tobina nie można sprowadzić do zera i jest ona stale równa

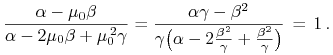$\frac{\alpha-\mu _{0}\beta}{\alpha-2\mu _{0}\beta+\mu _{0}^{{\, 2}}\gamma}=\frac{\alpha\gamma-\beta^{2}}{\gamma\big(\alpha-2\frac{\beta^{2}}{\gamma}+\frac{\beta^{2}}{\gamma}\big)}\,=\, 1\,.$

Prosta Tobina jest więc wtedy równoległa do ,, blaszki” $\{ 0\}\times\mathbb{R}^{k}$ i oddalona od niej o 1 – nie ma z nią żadnego punktu wspólnego. W szczególności jest rozłączna z prostą krytyczną Blacka, która w blaszce leży.

Po obłożeniu odwzorowaniem Markowitza $\mathcal{M}$ , prosta Tobina przechodzi na asymptoty pocisku Markowitza (Twierdzenie 8.1 (iii) ), rozłączne z samym pociskiem = obrazem prostej Blacka; patrz Figure VI w [23].
Należy wspomnieć, że inaczej [jako podwójna styczność poniżej i powyżej wartości $E_{0}$ ] było to ilustrowane w Rozdziale 4 książki [27], o czym pisze też Merton w przypisie 11 na stronie 1868 w [23].

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Analiza Portfelowa i Rynki Kapitałowe 1