9. Wykład IX, 27.XI.2009
W poprzednim wykładzie, oprócz drugiej wartości charakterystycznej
[stopy zwrotu ![]() bezryzykownej, gwarantowanej …], pojawiła się
też trzecia (po
bezryzykownej, gwarantowanej …], pojawiła się
też trzecia (po ![]() i
i ![]() ) charakterystyczna
wartość oczekiwana
) charakterystyczna
wartość oczekiwana ![]() .
(Oczywiście wartość ta pojawia się tylko wtedy, gdy napisany ułamek
ma sens, np gdy, jak w Uwadze 8.2,
.
(Oczywiście wartość ta pojawia się tylko wtedy, gdy napisany ułamek
ma sens, np gdy, jak w Uwadze 8.2, ![]() .) Na pionowej
osi
.) Na pionowej
osi ![]() mamy wtedy trzy wyróżnione wartości.
mamy wtedy trzy wyróżnione wartości.
Punktem wyjścia było – przypominamy – wzbogacenie modelowania Blacka
o wyidealizowany bank oferujący w obie strony jedną i tę samą (!)
stopę zwrotu ![]() . Albo równoważnie – dodanie do modelu Blacka
,,waloru bezryzykownego o stopie zwrotu
. Albo równoważnie – dodanie do modelu Blacka
,,waloru bezryzykownego o stopie zwrotu ![]() ”.
”.
Właśnie w Uwadze 8.2 (Wykład VIII) wspomnieliśmy, że w zmodyfikowanym
modelu Tobina zawsze zakłada się dodatkowo, że ![]() .
Za chwilę wyjaśnimy, dlaczego.
.
Za chwilę wyjaśnimy, dlaczego.
Na początek postawmy pytanie, co można wtedy powiedzieć o tej trzeciej
wyróżnionej wielkości ![]() ?
Zauważamy bez trudu, że
?
Zauważamy bez trudu, że
| (9.1) |
Istotnie, podstawową nierówność z Lematu 6.1 (Wykład VI,
![]() ) zapisujemy inaczej jako
) zapisujemy inaczej jako
![]() .
Teraz w procesie dzielenia tej nierówności stronami przez
.
Teraz w procesie dzielenia tej nierówności stronami przez
![]() nie zmieniamy kierunku
nierówności wtedy i tylko wtedy gdy
nie zmieniamy kierunku
nierówności wtedy i tylko wtedy gdy ![]() ,
i właśnie to jest powiedziane w (9.1).
,
i właśnie to jest powiedziane w (9.1).
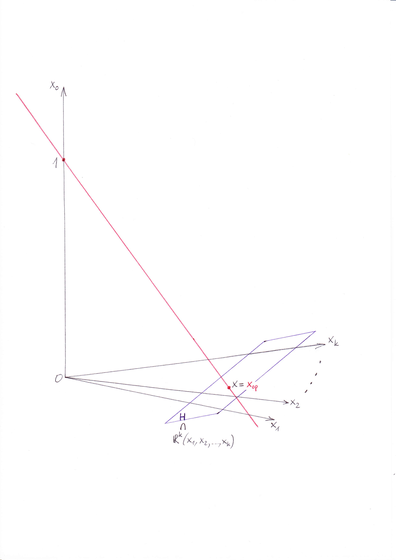
Zanim użyjemy równoważności (9.1), podsumujmy naszą dotychczasową wiedzę na temat zmodyfikowanego modelu Tobina.
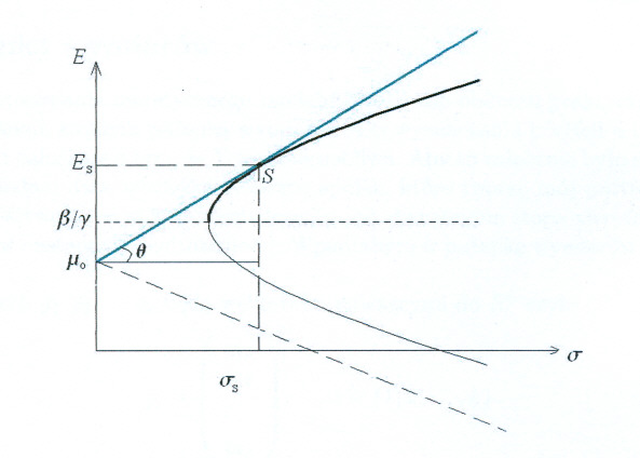
Kluczową rolę zdaje się odgrywać w nim prosta krytyczna Tobina,
utworzona z portfeli relatywnie minimalnego ryzyka (relatywnie =
przy ustalonej wartości oczekiwanej). W sytuacji ogólnej przechodzi
ona przez dwa charakterystyczne punkty-portfele mające wartości
oczekiwane ![]() (punkt położony na osi zmiennej
(punkt położony na osi zmiennej ![]() )
i
)
i ![]() (punkt leżący na ,,blaszce”
(punkt leżący na ,,blaszce” ![]() , istniejący tylko wtedy,
gdy ułamek ma sens, tj gdy
, istniejący tylko wtedy,
gdy ułamek ma sens, tj gdy ![]() ). Wygląda ona wtedy
tak [w wesji pdf rysunek trafia na następną stronę],
). Wygląda ona wtedy
tak [w wesji pdf rysunek trafia na następną stronę],
przy czym podprzestrzeń ![]() jest przez
nią trafiana w punkcie leżącym w hiperpłaszczyźnie
jest przez
nią trafiana w punkcie leżącym w hiperpłaszczyźnie ![]() (dokładniej: w
(dokładniej: w
![]() ), jak zostało ustalone w [bardzo łatwym] Ćwiczeniu 8.2
w Wykładzie VIII.
), jak zostało ustalone w [bardzo łatwym] Ćwiczeniu 8.2
w Wykładzie VIII.
Czy da się jeszcze powiedzieć coś więcej o tym punkcie spotkania
prostej Tobina z ![]() ?
Otóż tak,
?
Otóż tak,
Obserwacja. 9.1
Prosta krytyczna Tobina trafia podprzestrzeń ![]() w punkcie leżącym na prostej krytycznej Blacka:
w punkcie leżącym na prostej krytycznej Blacka:
w terminach wzoru (8.10) i oznaczeniach z Wykładu VI.
Dla dowodu wystarczy policzyć dwa minory ![]() wchodzące
do wzoru (6.2) na portfele krytyczne Blacka
wchodzące
do wzoru (6.2) na portfele krytyczne Blacka
![]() w Twierdzeniu 6.1 (Wykład VI):
w Twierdzeniu 6.1 (Wykład VI):
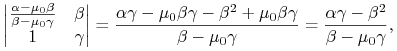 |
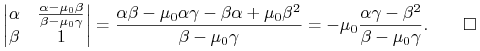 |
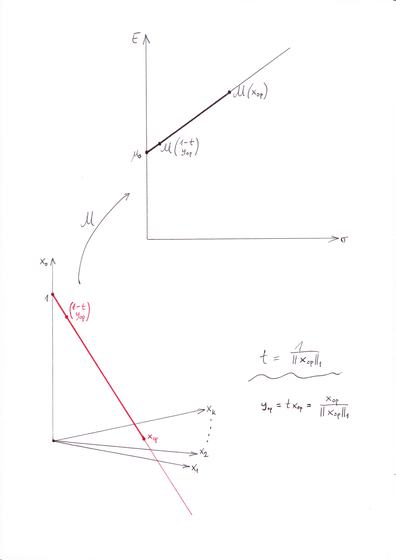
Ta obserwacja ma ważne konsekwencje geometryczne, gdyż ![]() –obrazy
prostych leżących w
–obrazy
prostych leżących w ![]() i przecinających prostą krytyczną Tobina
są zawsze, z powodu samej tylko krytyczności ich punktu przecięcia!,
styczne do
i przecinających prostą krytyczną Tobina
są zawsze, z powodu samej tylko krytyczności ich punktu przecięcia!,
styczne do ![]() –obrazu tej prostej Tobina, czyli do kątownika Tobina
policzonego w Wykładzie VIII.
–obrazu tej prostej Tobina, czyli do kątownika Tobina
policzonego w Wykładzie VIII.
W szczególności stosuje się to do prostej krytycznej Blacka,20Jest to tzw.
the punch line tego i być może wszystkich wykładów z APRK1. Anglosasi
mawiają w takich sytuacjach ”And now there comes the punch line …” o
ile tylko punkt przecięcia tych prostych istnieje. To znaczy – patrz końcówka
Wykładu VIII – gdy ![]() . Albo też, co jest dokładnie tym samym na mocy
równoważności (9.1), gdy
. Albo też, co jest dokładnie tym samym na mocy
równoważności (9.1), gdy ![]() .
.
Wtedy jej ![]() –obraz, czyli pocisk Markowitza, jest styczny w punkcie
–obraz, czyli pocisk Markowitza, jest styczny w punkcie
![]() do kątownika Tobina. Przy tym pocisk leży oczywiście wewnątrz tego
kątownika – bo brzeg kątownika Tobina jest, jak już wiemy z Wykładu VIII,
granicą minimalną w zmodyfikowanym modelu Tobina.
do kątownika Tobina. Przy tym pocisk leży oczywiście wewnątrz tego
kątownika – bo brzeg kątownika Tobina jest, jak już wiemy z Wykładu VIII,
granicą minimalną w zmodyfikowanym modelu Tobina.
W tym miejscu bardzo zalecane jest obejrzeć dwie ilustracje, Figure V i
Figure VII, w fundamentalnej (choć trudno dostępnej) pracy [23].
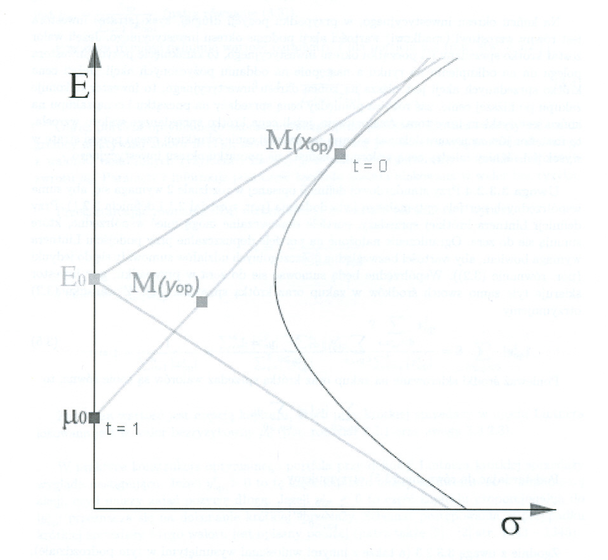
Dla dalszej dyskusji kluczowe jest, czy ![]() , czy też
, czy też ![]() .
.
![]() W pierwszym przypadku rzędna punktu styczności
W pierwszym przypadku rzędna punktu styczności
| (9.2) |
co pokazuje, że punkt styczności leży i na górnym ramieniu kątownika Tobina, i na górnym ,,wąsie” pocisku Markowitza. Czytelnik domyśla się już, że tylko ta sytuacja będzie dla nas ciekawa (maksymalizowany będzie współczynnik Sharpe'a, o którym wstępnie dowiedzieliśmy się już w Wykładzie I).
I czytelnik domyśla się także, co dzieje się w drugim przypadku.
![]() Tak jest, wtedy, znowu używając (9.1),
Tak jest, wtedy, znowu używając (9.1),
| (9.3) |
więc punkt styczności leży zarówno na dolnym ramieniu kątownika Tobina, jak też na dolnym wąsie pocisku Markowitza – co z punktu widzenia analizy portfelowej jest zupełnie nieciekawe (punkt przecięcia prostych byłby portfelem nieefektywnym w aspekcie B, współczynnik Sharpe'a byłby wtedy minimalizowany). Ilustracją tej sytuacji jest Figure VII w [23]; patrz też ciekawe uwagi w przypisie 11 tamże, korygujące jeszcze wcześniejsze próby ilustrowania podejmowane przez innych autorów.
Jak tę wewnętrzną styczność pocisku Markowitza do kątownika Tobina można zobrazować geometrycznie, ograniczając się do portfelowo ciekawszej sytuacji (9.2)? Pierwsza historycznie ilustracja tego to właśnie Figure V w publikacji [23].
W tych wykładach za pierwszą próbę wizualizacji możnaby od biedy i ex post uznać … Rysunek 1.3 w Wykładzie I. A oto jeszcze cztery próby takiej wizualizacji, na czterech rysunkach idących jeden po drugim tu poniżej, pochodzących z prac licencjackich czterech różnych studentów naszego wydziału. (Nikt na Wydziale MIM UW, jak dotąd, nie zobrazował lepiej wewnętrznej styczności pocisku Markowitza do kątownika Tobina.)
Oznaczenia na każdym z rysunków są różne; nie ma zresztą jakiejś jednej kanonicznej terminologii przyjętej w ośrodkach badawczych, gdzie uprawiana jest analiza portfelowa. [W wersji pdf dwie z tych wizualizacji zajmują następną stronę, kolejna jest na jeszcze następnej stronie, zaś czwarta i ostatnia wizualizacja znajduje się na jeszcze jeszcze następnej.]
Ćwiczenie 9.1
Uzasadnić tę styczność [pocisku Markowitza do kątownika Tobina] bezpośrednim rachunkiem.
Styczna do hiperboli ![]() w punkcie
w punkcie ![]() ma równanie
ma równanie ![]() [to cytat z przedwojennego
licealnego podręcznika geometrii].
[to cytat z przedwojennego
licealnego podręcznika geometrii].
Równanie stycznej do hiperboli
w punkcie
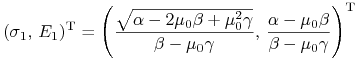 |
jest więc postaci
Mamy:
zatem, po podstawieniu wszystkich parametrów, styczna ma postać
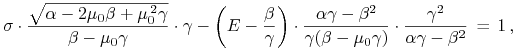 |
co po skróceniu i obustronnym pomnożeniu przez
![]() daje równanie
daje równanie
Upraszczając, dostajemy równanie stycznej w ostatecznej postaci
(porównaj też jeszcze raz Figure IV oraz Figure V w [23]). Jest to równanie górnego ramienia kątownika Tobina.
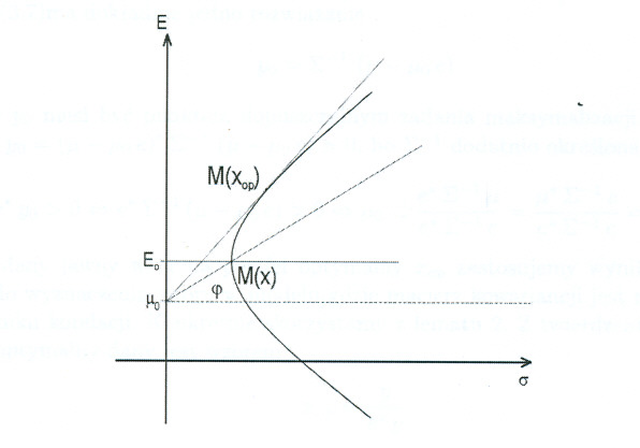
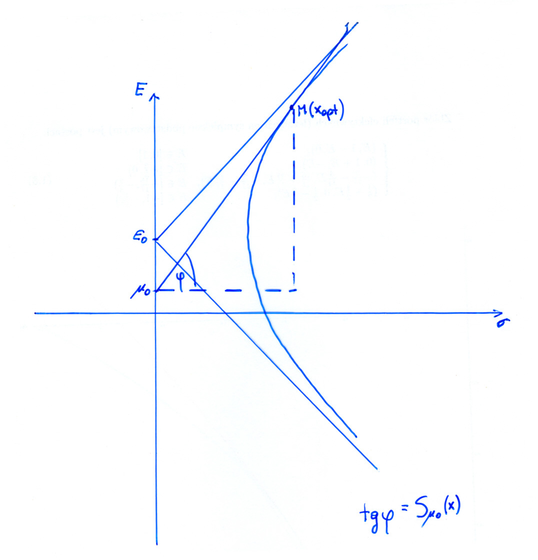
Dokładniejsze przyjrzenie się Rysunkowi 9.2 pokazuje, że portfel krytyczny Blacka
| (9.4) |
podany tu w postaci uzyskanej w (8.10) w Wykładzie VIII,
w sytuacji (9.2) maksymalizuje wśród wszystkich
portfeli Blacka ![]() współczynnik Sharpe'a
współczynnik Sharpe'a
(powtórzenie wzoru (1.1) z Wykładu I). Jest to bezpośredni wniosek z Rysunku 9.2; porównaj też Rysunek 1.3 (i jego okolice) w Wykładzie I.
Natomiast w dualnej sytuacji (9.3), portfel (8.10), leżący niezmiennie na przecięciu prostych Blacka i Tobina, minimalizuje ten sam współczynnik wśród wszystkich portfeli Blacka, czego uzasadnienie jest zupełnie analogiczne i też geometryczne.
Wreszcie w sytuacji specjalnej ![]() , zagadnienie maksymalizacji
(czy też analogicznie minimalizacji) współczynnika Sharpe'a nie
ma rozwiązania wśród wszystkich portfeli Blacka. Istotnie, dla każdego
portfela Blacka nietrudno wtedy wskazać inny portfel, którego współczynnik
Sharpe'a jest większy (względnie mniejszy). Nie wchodzimy tu w szczegóły,
jest to całkiem elementarne.
, zagadnienie maksymalizacji
(czy też analogicznie minimalizacji) współczynnika Sharpe'a nie
ma rozwiązania wśród wszystkich portfeli Blacka. Istotnie, dla każdego
portfela Blacka nietrudno wtedy wskazać inny portfel, którego współczynnik
Sharpe'a jest większy (względnie mniejszy). Nie wchodzimy tu w szczegóły,
jest to całkiem elementarne.
Będziemy odtąd mówić, nie wymieniając, czy nie nawiązując już wprost do
wyidealizowanego banku, że w sytuacji (9.2) portfel ![]() jest optymalny w modelu Blacka ze względu na [panującą na rynku]
stopę bezryzykowną
jest optymalny w modelu Blacka ze względu na [panującą na rynku]
stopę bezryzykowną ![]() . Jest to pewien żargon matematyki
finansowej, lecz dość szeroko rozpowszechniony. Pierwszy taką terminologię
wprowadził Krzyżewski w [13]; mówił on o portfelu optymalnym
w modelu Blacka względem
. Jest to pewien żargon matematyki
finansowej, lecz dość szeroko rozpowszechniony. Pierwszy taką terminologię
wprowadził Krzyżewski w [13]; mówił on o portfelu optymalnym
w modelu Blacka względem ![]() .
.
Dyskusja rozpoczęta w Wykładzie VIII i kontynuowana do tego miejsca w bieżącym, pozwala na sformułowanie
Twierdzenie 9.1
W niezdegenerowanym modelu Blacka istnieje portfel optymalny ze względu
na stopę bezryzykowną
![]() .
.
Gdy ![]() jest właśnie taka, wtedy portfel optymalny ze względu na
stopę
jest właśnie taka, wtedy portfel optymalny ze względu na
stopę ![]() jest jedyny i dany wzorem (9.4).
jest jedyny i dany wzorem (9.4).
To twierdzenie jest już udowodnione; również, jeśli chodzi o jedyność
portfela optymalnego. (W grę wchodzą bowiem tylko portfele Blacka mające
![]() -obrazy na górnym wąsie pocisku Markowitza, więc leżące
tylko na jednej półprostej
-obrazy na górnym wąsie pocisku Markowitza, więc leżące
tylko na jednej półprostej ![]() w prostej Blacka, o początku
w
w prostej Blacka, o początku
w ![]() . Zaś na tej półprostej maksymalny współczynnik Sharpe'a
ma tylko portfel
. Zaś na tej półprostej maksymalny współczynnik Sharpe'a
ma tylko portfel ![]() .)
.)
Uwaga 9.1
(i) Współczynnik Sharpe'a to jedna z najważniejszych miar
efektywności portfela w całej analizie portfelowej. Współczynnik
ten mierzy premię za ryzyko, czyli nadwyżkę stopy zwrotu
ponad ![]() , w stosunku do samego ryzyka portfela –
wyraża więc premię za ryzyko portfela na jednostkę tego
ryzyka. Zwracamy uwagę, że współczynnik Sharpe'a już był
wzmiankowany, w tym dokładnie kontekście, w Wykładzie I.
, w stosunku do samego ryzyka portfela –
wyraża więc premię za ryzyko portfela na jednostkę tego
ryzyka. Zwracamy uwagę, że współczynnik Sharpe'a już był
wzmiankowany, w tym dokładnie kontekście, w Wykładzie I.
(ii) Podkreślamy, że portfel ![]() ma podaną wyżej
interpretację (maksymalizacja współczynnika Sharpe'a) na
płaszczyźnie
ma podaną wyżej
interpretację (maksymalizacja współczynnika Sharpe'a) na
płaszczyźnie ![]() , nie zaś
, nie zaś ![]() !
Interpretacja dotyczy prostych i hiperbol, nie parabol.
Przykład portfela, który mógłby być traktowany jako
!
Interpretacja dotyczy prostych i hiperbol, nie parabol.
Przykład portfela, który mógłby być traktowany jako
![]() (zaczerpnięty z [4]), pojawił
się już na początku Wykładu VI. Dalsze przykłady są
podane tu poniżej (Przykłady 9.1 i 9.2).
(zaczerpnięty z [4]), pojawił
się już na początku Wykładu VI. Dalsze przykłady są
podane tu poniżej (Przykłady 9.1 i 9.2).
Przykład 9.1
W modelu Blacka z danymi z Przykładu 5.2 przy ![]() ,
,
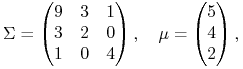 |
próbujemy wyliczyć specjalną wartość stopy bezryzykownej
![]() , przy której portfelem optymalnym jest
, przy której portfelem optymalnym jest ![]() .
.
Bardzo pomocny jest Rysunek 5.3. Z jego pomocą wnioskujemy, że taka sama będzie odpowiedź dla podmodelu Blacka używającego tylko spółek numer 1 i 2:21Względnie 2 i 3, my wybieramy 1 i 2. To będzie w przyszłości nasz częsty ,,stały element gry” – ograniczanie się do podmodelu i stosowanie do niego, czy w nim, tej samej teorii, co dla pełnego modelu. Zresztą pierwszy krok w tym kierunku był już zrobiony w Ćwiczeniu 7.3 w Wykładzie VII, gdy, w aspekcie M, szukaliśmy początku łamanej efektywnej na pewnym boku trójkąta.
Istotnie, portfel ![]() jest tu portfelem krytycznym, więc styczna
do pocisku Markowitza w jego obrazie pokrywa się ze styczną do obrazu
boku
jest tu portfelem krytycznym, więc styczna
do pocisku Markowitza w jego obrazie pokrywa się ze styczną do obrazu
boku ![]() i możemy pracować z tą ,,drugą” styczną,
to znaczy ograniczyć się do wspomnianego podmodelu. Trochę to
niepokojące, ale … trudne do podważenia.
i możemy pracować z tą ,,drugą” styczną,
to znaczy ograniczyć się do wspomnianego podmodelu. Trochę to
niepokojące, ale … trudne do podważenia.
By – odpowiednio teraz rozumiany, w wymiarze 2! – wzór (9.4)
dawał ![]() , zerować się musi pierwsza składowa w jego liczniku.
Tymczasem ten licznik (wielkość wektorowa), z dokładnością do
czynnika liczbowego
, zerować się musi pierwsza składowa w jego liczniku.
Tymczasem ten licznik (wielkość wektorowa), z dokładnością do
czynnika liczbowego ![]() , to
, to
Stąd odpowiedzią jest ![]() . Środkowy z trzech walorów
okazuje się być optymalny w modelu Blacka przy stopie bezryzykownej
równej wartości oczekiwanej najsłabszego (czyli trzeciego) z walorów.
. Środkowy z trzech walorów
okazuje się być optymalny w modelu Blacka przy stopie bezryzykownej
równej wartości oczekiwanej najsłabszego (czyli trzeciego) z walorów.
Przykład 9.2
W modelu Blacka z danymi studenta Mordona
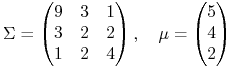 |
(znowu sięgamy do Przykładu 5.2 w Wykładzie V, a nawet do praźródła
tamtego przykładu), ![]() ,
, ![]() ,
zatem pocisk Markowitza ma dzióbek na wysokości
,
zatem pocisk Markowitza ma dzióbek na wysokości
![]() .
Bierzemy
.
Bierzemy ![]() dosyć duże w stosunku do
dosyć duże w stosunku do ![]() , by wydobyć
dynamikę tkwiącą we wzorze (9.4) na portfel optymalny:
, by wydobyć
dynamikę tkwiącą we wzorze (9.4) na portfel optymalny:
gdy ![]() , wtedy
, wtedy
![]() .
.
Gdy zaś ![]() , wtedy
, wtedy ![]() .
.
Dynamika ilustrowana w Przykładzie 9.2 jest całkowicie zrozumiała,
gdy rysunki takie jak [np] Rysunek 9.2 analizujemy pod kątem dążności
![]() : punkt styczności, czyli
: punkt styczności, czyli ![]() ,
ucieka wtedy w górę (w kierunku `północno-wschodnim') po wąsie
pocisku Markowitza do
,
ucieka wtedy w górę (w kierunku `północno-wschodnim') po wąsie
pocisku Markowitza do ![]() .
.
Ćwiczenie 9.2 (kontynuacja ćwiczenia z Uwagi 7.2 (Wykład VII))
Znaleźć wartość stopy bezryzykownej ![]() , względem której
portfel
, względem której
portfel ![]() jest optymalny w modelu Blacka
z parametrami (7.1), który pojawił się jeszcze w
Wykładzie VII. Czy w tym modelu Blacka są jeszcze inne
portfele optymalne względem tej wartości
jest optymalny w modelu Blacka
z parametrami (7.1), który pojawił się jeszcze w
Wykładzie VII. Czy w tym modelu Blacka są jeszcze inne
portfele optymalne względem tej wartości ![]() ?
Jeśli tak, to znaleźć wszystkie takie portfele
[optymalne w tym modelu Blacka względem tej wartości
?
Jeśli tak, to znaleźć wszystkie takie portfele
[optymalne w tym modelu Blacka względem tej wartości ![]() ].
].
W tym samym modelu Blacka znaleźć wszystkie portfele
optymalne względem stopy bezryzykownej ![]() .
.
Dyskusja portfeli optymalnych w teorii Blacka byłaby niepełna bez
dyskusji portfeli efektywnych w zmodyfikowanym modelu Tobina,
leżących na półprostej krytycznej Tobina zaczynającej się w
portfelu ![]() i przechodzącej przez
i przechodzącej przez
![]() .
Ta półprosta jest zaznaczona na czerwono na Rysunku 9.6 poniżej.
One, i tylko one, są efektywne, gdyż tylko one przechodzą na górne
ramię kątownika Tobina, tzn.
.
Ta półprosta jest zaznaczona na czerwono na Rysunku 9.6 poniżej.
One, i tylko one, są efektywne, gdyż tylko one przechodzą na górne
ramię kątownika Tobina, tzn. ![]() .
W szczególności odcinek portfeli między punktami charakterystycznymi
na prostej Tobina
.
W szczególności odcinek portfeli między punktami charakterystycznymi
na prostej Tobina ![]() i
i ![]() przechodzi afinicznie na odcinek o końcach
przechodzi afinicznie na odcinek o końcach ![]() i
i ![]() .22Formalnie rzecz
biorąc, nie powinniśmy w argumencie pod
.22Formalnie rzecz
biorąc, nie powinniśmy w argumencie pod ![]() opuszczać
zerowej składowej
opuszczać
zerowej składowej ![]() .
Te odcinki są pogrubione na Rysunku 9.6 poniżej.
.
Te odcinki są pogrubione na Rysunku 9.6 poniżej.
Na rzucie wymienionego odcinka [czerwonego pogrubionego
na Rysunku 9.6] na ![]() leży ważny z punktu
widzenia interpretacji finansowych ,,portfel”
leży ważny z punktu
widzenia interpretacji finansowych ,,portfel”
| (9.5) |
Uwaga. Jest częstym błędem w pracach licencjackich czy nawet
podręcznikach lokować punkt ![]() na czerwonym pogrubionym
odcinku na Rysunku 9.6. Punkty tam leżące są pewnymi portfelami
krytycznymi Tobina i oczywiście spełniają warunek budżetowy.
Ślad tego błędu jest też na, skądinąd bardzo starannym i
czytelnym, Rysunku 9.2 powyżej.
na czerwonym pogrubionym
odcinku na Rysunku 9.6. Punkty tam leżące są pewnymi portfelami
krytycznymi Tobina i oczywiście spełniają warunek budżetowy.
Ślad tego błędu jest też na, skądinąd bardzo starannym i
czytelnym, Rysunku 9.2 powyżej.
Ćwiczenie 9.3
Gdzie dokładnie jest błąd na Rysunku 9.2?
Przeprowadzić analizę porównawczą Rysunków 9.2 i 9.6.
Cudzysłów przed definicją (9.5) został więc użyty
celowo; obiekt opisany wzorem (9.5) najczęściej nie
jest portfelem. Dokładniej, oznaczając ![]() , na czerwonym
pogrubionym odcinku poniżej leży portfel krytyczny Tobina
, na czerwonym
pogrubionym odcinku poniżej leży portfel krytyczny Tobina
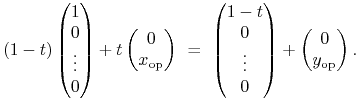 |
(9.6) |
[W wersji pdf odpowiedni rysunek przeskoczył aż na następną stronę.]
Chcemy te ogólne uwagi wstępne wesprzeć konkretnym przykładem.
Jeśli portfel wypisany explicite w Wykładzie VI oznaczyć właśnie
![]() , wtedy (rezygnując z
, wtedy (rezygnując z ![]() na rzecz zwykłych
ułamków)
na rzecz zwykłych
ułamków) ![]() , zaś
, zaś ![]() zdefiniowany wzorem (9.5) wynosi
zdefiniowany wzorem (9.5) wynosi
| Walor nr | Udział w ,,portfelu” |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Zgodnie we wzorem (9.6), do tak określonego wektora
![]() dochodzi ogromna część kapitału (tylko kapitału
własnego inwestora, o czym niżej!), dokładnie (
dochodzi ogromna część kapitału (tylko kapitału
własnego inwestora, o czym niżej!), dokładnie (![]() )
–część zdeponowana w banku na bezryzykownym koncie procentującym
)
–część zdeponowana w banku na bezryzykownym koncie procentującym
![]() w rozważanym okresie inwestycyjnym, patrz wzór (9.8)
poniżej.
w rozważanym okresie inwestycyjnym, patrz wzór (9.8)
poniżej.
,,Portfel” ![]() jest nazywany w literaturze
portfelem optymalnym Lintnera, por. [16]
i [5]. Wyraża on, czy modeluje (koduje?) inwestowanie
na giełdzie z ograniczoną w sensie Lintnera krótką sprzedażą;
w danym przypadku – inwestowanie optymalne w sensie współczynnika
Sharpe'a
jest nazywany w literaturze
portfelem optymalnym Lintnera, por. [16]
i [5]. Wyraża on, czy modeluje (koduje?) inwestowanie
na giełdzie z ograniczoną w sensie Lintnera krótką sprzedażą;
w danym przypadku – inwestowanie optymalne w sensie współczynnika
Sharpe'a ![]() .
.
Przed dalszymi wyjaśnieniami chcemy podkreślić występującą tu
pozorną sprzeczność. Oto z jednej strony ,,portfel” ![]() niesie w sobie kompletną informację dotyczącą inwestowania w akcje:
suma modułów jego składowych wynosi z definicji 1,
czyli przedstawia on podział kapitału własnego inwestora na
części inwestowane w poszczególne spółki giełdowe. Ponadto
znaki wskazują na rodzaj tego inwestowania:
niesie w sobie kompletną informację dotyczącą inwestowania w akcje:
suma modułów jego składowych wynosi z definicji 1,
czyli przedstawia on podział kapitału własnego inwestora na
części inwestowane w poszczególne spółki giełdowe. Ponadto
znaki wskazują na rodzaj tego inwestowania: ![]() oznacza zajmowanie długiej pozycji w danym walorze, zaś
oznacza zajmowanie długiej pozycji w danym walorze, zaś ![]() oznacza zajmowanie krótkiej pozycji.
oznacza zajmowanie krótkiej pozycji.
Wszystko wydaje się pasować, dopóki nie uzmysłowimy sobie, że jednak
![]() nie jest portfelem, zaś staje się takim
dopiero po dołożeniu czy też dostrzeżeniu lwiej części środków pieniężnych
umieszczonych na bezryzykownym koncie w banku. Czy można w jakiś
finansowo spójny sposób połączyć wymienione tu fakty i informacje?
nie jest portfelem, zaś staje się takim
dopiero po dołożeniu czy też dostrzeżeniu lwiej części środków pieniężnych
umieszczonych na bezryzykownym koncie w banku. Czy można w jakiś
finansowo spójny sposób połączyć wymienione tu fakty i informacje?
Otóż tak, przy czym wyjaśnienie przychodzi z dwu stron.
Pierwsza jest algebraiczna i polega na uważnym przyjrzeniu się wielkości środków, które trafiają do banku:
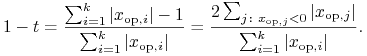 |
(9.7) |
Druga polega na przyjrzeniu się inwestowaniu w akcje z
dopuszczeniem krótkiej sprzedaży w sensie Lintnera. Podkreślmy –
jakiemukolwiek takiemu inwestowaniu, niekoniecznie inwestowaniu w
portfel ![]() pochodzący od portfela optymalnego w
modelu Blacka.
pochodzący od portfela optymalnego w
modelu Blacka.
Otóż Lintner modeluje inwestowanie w portfel ![]() z krótką sprzedażą
następująco:
z krótką sprzedażą
następująco:
inwestor wkracza do Domu Maklerskiego ze swoim kapitałem ![]() , który
dzieli na części
, który
dzieli na części ![]() przeznaczone do zainwestowania w akcje spółek
o numerach
przeznaczone do zainwestowania w akcje spółek
o numerach ![]() ,
, ![]() . Jeśli zajmuje on długą pozycję
w walorze
. Jeśli zajmuje on długą pozycję
w walorze ![]() , wtedy
, wtedy ![]() . Jeśli krótką, wtedy
. Jeśli krótką, wtedy ![]() . W tym
drugim, ciekawszym przypadku inwestor:
. W tym
drugim, ciekawszym przypadku inwestor:
-
- deponuje w DM
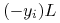 swego kapitału, czyli równowartość
akcji
swego kapitału, czyli równowartość
akcji 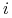 -tej spółki pożyczonych przez DM;
-tej spółki pożyczonych przez DM;
-
- następnie sprzedaje te dopiero co pożyczone akcje i uzyskane za nie
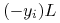 zamraża na cały okres inwestycyjny w DM,
po angielsku: put in escrow;
zamraża na cały okres inwestycyjny w DM,
po angielsku: put in escrow;
-
- na końcu okresu inwestycyjnego odbiera pieniądze put in escrow i odkupuje za nie pożyczone na początku akcje nr
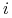 (za
mniejszą kwotę, niż zamroził – wtedy ma zysk, lub za większą –
wtedy różnicę musi dołożyć z własnych środków i wówczas odnotowuje
stratę), które następnie zwraca do DM;
(za
mniejszą kwotę, niż zamroził – wtedy ma zysk, lub za większą –
wtedy różnicę musi dołożyć z własnych środków i wówczas odnotowuje
stratę), które następnie zwraca do DM;
-
- wychodząc z DM odbiera swoje zdeponowane na okres inwestycyjny
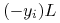 .
.
Unifikacja spojrzeń na krótką sprzedaż Lintnera następuje przez zapisanie (9.7) w postaci
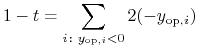 |
(9.8) |
i następnie ekstrapolację tego wzoru do ogólniejszego
| (9.9) |
gdzie ![]() .
.
Podkreślamy jeszcze raz – portfel ![]() modelujący krótką sprzedaż Lintnera nie pochodzi teraz od żadnego
portfela optymalnego. Jedyne ograniczenie, jakiemu podlega, to
modelujący krótką sprzedaż Lintnera nie pochodzi teraz od żadnego
portfela optymalnego. Jedyne ograniczenie, jakiemu podlega, to
![]() , tzn. inwestor inwestuje więcej w długie
pozycje niż w krótkie.23 Nawet to ograniczenie à priori
nie jest konieczne w podejściu Lintnera. Jednakże nasze interpretacje
dotyczą tylko portfeli Lintnera, w których więcej niż połowa kapitału
idzie w długie pozycje, a mniej niż połowa w pozycje krótkie.
, tzn. inwestor inwestuje więcej w długie
pozycje niż w krótkie.23 Nawet to ograniczenie à priori
nie jest konieczne w podejściu Lintnera. Jednakże nasze interpretacje
dotyczą tylko portfeli Lintnera, w których więcej niż połowa kapitału
idzie w długie pozycje, a mniej niż połowa w pozycje krótkie.
Kluczowe dla zrozumienia sytuacji jest zauważenie, że
zarówno początkowe pieniądze inwestora ![]() zdeponowane
w DM, jak i te ,,nowe”
zdeponowane
w DM, jak i te ,,nowe” ![]() zamrożone, czy też put in escrow
na okres inwestycyjny, procentują ze stopą zysku
zamrożone, czy też put in escrow
na okres inwestycyjny, procentują ze stopą zysku ![]() !
DM nie trzyma przecież takich depozytów u siebie, tylko w banku,
który zawsze stosuje stopę
!
DM nie trzyma przecież takich depozytów u siebie, tylko w banku,
który zawsze stosuje stopę ![]() . Innymi słowy, dla każdej
spółki nr
. Innymi słowy, dla każdej
spółki nr ![]() , w której inwestor zajmuje krótką pozycję (
, w której inwestor zajmuje krótką pozycję (![]() ),
przez okres inwestycyjny procentuje dla niego kwota
),
przez okres inwestycyjny procentuje dla niego kwota ![]() .
Łącznie procentuje tak zatem kwota
.
Łącznie procentuje tak zatem kwota ![]() [wielkość po prawej stronie
wzoru (9.9)]. Czy inwestor Lintnera tego chce, czy nie,
efekt jest taki, jakby
[wielkość po prawej stronie
wzoru (9.9)]. Czy inwestor Lintnera tego chce, czy nie,
efekt jest taki, jakby ![]() -ta część jego kapitału procentowała
bezryzykownie ze stopą
-ta część jego kapitału procentowała
bezryzykownie ze stopą ![]() .
.
Natomiast pozostała ![]() -ta część jego kapitału zachowuje się
proporcjonalnie ze współczynnikiem
-ta część jego kapitału zachowuje się
proporcjonalnie ze współczynnikiem ![]() do zachowania na giełdzie
portfela – już teraz prawdziwego portfela Blacka
do zachowania na giełdzie
portfela – już teraz prawdziwego portfela Blacka
![]() :
:
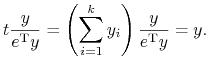 |
Im mniejszy jest ,,portfel” Lintnera ![]() ,
, ![]() małe dodatnie, tym
większa jest ilość środków,
małe dodatnie, tym
większa jest ilość środków, ![]() w stosunku do kapitału inwestora,
realnie lokowana w banku. Im większa skłonność do krótkiej sprzedaży,
tym większa część środków bezryzykownie ,,pracuje” w banku.
Taka jest istota ograniczonej krótkiej sprzedaży Lintnera.
w stosunku do kapitału inwestora,
realnie lokowana w banku. Im większa skłonność do krótkiej sprzedaży,
tym większa część środków bezryzykownie ,,pracuje” w banku.
Taka jest istota ograniczonej krótkiej sprzedaży Lintnera.
Dla wygody słuchacza, któremu przypadła do gustu krótka sprzedaż w sensie Lintnera, proponujemy następujący krótki słownik:
| portfel Blacka |
”portfel” Lintnera 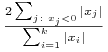 – część kapitału inwestora, por. (9.7)
– część kapitału inwestora, por. (9.7) |
|
| portfel Blacka |
”portfel” Lintnera |
Uwaga 9.2
Należy cały czas pamiętać, że krótka sprzedaż Lintnera może też
wykraczać poza opisany tu schemat. Można w niej dokładnie połowę
kapitału inwestować w krótkie pozycje, można ![]() , można
, można
![]() , … Patrz też uwagi na ten temat w [5],
przypis 4 oraz [4], przypis 4 na str. 230.
, … Patrz też uwagi na ten temat w [5],
przypis 4 oraz [4], przypis 4 na str. 230.
Uwaga 9.3
Dużo bardziej realistycznie, niż Black czy Lintner, modelował krótką sprzedaż akcji na giełdzie G. J. Alexander w pracy [2]. Jego podejście jest szczegółowo dyskutowane na wykładzie APRK2.
Dla zamknięcia tematu ,,zmodyfikowany model Tobina” warto spojrzeć na oba typy kątowników: stary w teorii Blacka (mówimy krótko ”kątownik Blacka”) i nowy w teorii Tobina (”kątownik Tobina”) z jednego wspólnego punktu widzenia.
Mianowicie, zmodyfikowany model Tobina okazuje się leżeć ,,na granicy”
pewnych niezdegenerowanych modeli Blacka ![]() z parametrami
z parametrami
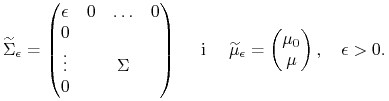 |
Dokładniej, dla tych modeli można policzyć klasyczne parametry z teorii
Blacka ![]() , uzyskując:
, uzyskując:
Wówczas wysokości dzióbków ich pocisków Markowitza zachowują się zgodnie z oczekiwaniami
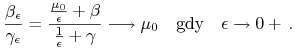 |
(9.10) |
Co z kątami między asymptotami tych pocisków, albo najkrócej: co z kątami w ich kątownikach Blacka? Liczymy tangensy połowy kątów w kątownikach Blacka dla tych modeli, wzór (6.6):
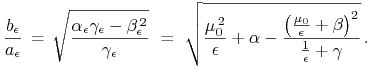 |
Ćwiczenie 9.4
Jest pouczającym ćwiczeniem24choć to niby jest tylko AM I …
policzyć granicę tego wyrażenia przy ![]() .
.
Ta granica wynosi ![]() ,
co wydaje się dość naturalne.
,
co wydaje się dość naturalne.
Do kompletu informacji brak jeszcze wiedzy na temat samych półoś
![]() oraz
oraz ![]() pocisków Markowitza, które mają
do czegoś dążyć. Z poziomymi półosiami nie ma najmniejszego kłopotu,
pocisków Markowitza, które mają
do czegoś dążyć. Z poziomymi półosiami nie ma najmniejszego kłopotu,
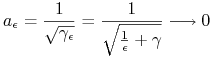 |
gdy ![]() . (Podobnie z pionowymi półosiami, gdy już
– właśnie z Ćwiczenia 9.4 ! – znamy granicę tangensów kątów:
. (Podobnie z pionowymi półosiami, gdy już
– właśnie z Ćwiczenia 9.4 ! – znamy granicę tangensów kątów:
lecz nam wystarcza informacja o półosiach poziomych.)
Tak więc dany zmodyfikowany model Tobina istotnie jest granicą pewnych
niezdegenerowanych modeli Blacka w wymiarze ![]() , z naciskiem na ”pewnych”,
specjalnie dobranych. Ich kątowniki Blacka dążą do kątownika Tobina, ok,
lecz nawet więcej: same te pociski Markowitza dążą do kątownika
Tobina.25W tym momencie przypomina się nam Rysunek 4.5
w Wykładzie IV: pocisk Markowitza oglądany z tak daleka, że
już nieodróżnialny od własnych asymptot.
, z naciskiem na ”pewnych”,
specjalnie dobranych. Ich kątowniki Blacka dążą do kątownika Tobina, ok,
lecz nawet więcej: same te pociski Markowitza dążą do kątownika
Tobina.25W tym momencie przypomina się nam Rysunek 4.5
w Wykładzie IV: pocisk Markowitza oglądany z tak daleka, że
już nieodróżnialny od własnych asymptot.
Konkludując, [ktoś powie:] nic nowego pod słońcem; zmodyfikowany model Tobina może być w bardzo precyzyjnym sensie traktowany jako przypadek graniczny w teorii Blacka i współpracowników.
Chcemy teraz przenieść spojrzenie Tobina na model Blacka na – też Tobina – spojrzenie na model Markowitza! Pamiętamy, że w teorii Blacka portfel optymalny ze względu na stopę bezryzykowną podaną przez teorię Tobina wyłonił się całkiem naturalnie. Maksymalizowanie przez niego współczynnika Sharpe'a jest widoczne bezpośrednio i jest bardzo intuicyjne.
Inaczej będzie z portfelami optymalnymi w teorii Markowitza.
Metody Analizy II bezpośrednio tam nie wystarczą, potrzebna będzie
Optymalizacja II. Więcej nawet: do samego szukania granicy minimalnej
![]() w ogólnym przypadku też użyteczna będzie Optymalizacja II.
w ogólnym przypadku też użyteczna będzie Optymalizacja II.
Kluczowe narzędzie dla całej pozostałej części kursu APRK1
Przypomnimy teraz ważne narzędzie z Optymalizacji II, tzw. twierdzenie
Karusha-Kuhna-Tuckera, które oryginalnie opublikowane zostało w
[14], tzn. w trudno dostępnej publikacji zbiorowej ,,Proceedings
![]() Berkeley Symposium on Mathematical Statistics and Probability”
(1951) oraz było już zawarte w nieopublikowanej pracy
magisterskiej [11] z [grudnia] roku 1939. Twierdzenie to prawie
zawsze przypisywane jest tylko Kuhnowi i Tuckerowi; niżej (i w dalszych
wykładach) czytelnik znajdzie niemało prób wyjaśnienia takiego stanu
rzeczy.
Berkeley Symposium on Mathematical Statistics and Probability”
(1951) oraz było już zawarte w nieopublikowanej pracy
magisterskiej [11] z [grudnia] roku 1939. Twierdzenie to prawie
zawsze przypisywane jest tylko Kuhnowi i Tuckerowi; niżej (i w dalszych
wykładach) czytelnik znajdzie niemało prób wyjaśnienia takiego stanu
rzeczy.
Należy zaznaczyć, że oryginalne sformułowania twierdzenia, bardzo do siebie
zbliżone, choć podane całkowicie niezależnie przez (a) Karusha oraz
(b) Kuhna i Tuckera, były inne niż przytoczone tu poniżej.
Nie miały one charakteru `iff' (czyli, po nowo-polsku, `wteddy') i
nie było w nich żadnych słów dotyczących wklęsłości bądź wypukłości.
Były to tylko warunki konieczne ekstremów lokalnych warunkowych
konkretnego typu; w istocie jeden warunek wspólny w obu pracach.
Jest to znakomicie opisane w – dużo późniejszej – przeglądowej
i historycznej pracy [12], gdzie szczególnie należy zwrócić
uwagę na początek sekcji 2.3 na stronie 337, jako, że na pierwszy
rzut oka warunek Karusha jednak różni się od warunku(ów) Kuhna
i Tuckera.
Piszący kilkanaście lat później [w dużym przeglądowym artykule w Wiadomościach Matematycznych XII.1 (1969)] A. Turowicz i H. Górecki tak oceniali to twierdzenie: ”… Metody Dubowickiego–Milutina oraz Kuhna–Tuckera są tak doniosłe, że powinny być udostępnione inżynierom pracującym naukowo w specjalnym opracowaniu.” (O pracy magisterskiej Karusha nic wtedy, a może i później, nie wiedzieli.)
Dopiero po jakimś czasie dyskutowane twierdzenie zaczęło być
używane w kategorii wypukłej, i wówczas już jako `wteddy'.
Nie sposób obecnie odtworzyć łańcuszka tego swoistego głuchego
telefonu, który w danym przypadku ulepszał, a nie pogarszał rezultat!
Oto wersja, jaka nam będzie potrzebna i (chwilowo) wystarczająca.
Twierdzenie 9.2 (Karush; Kuhn, Tucker; wersja w kategorii wypukłej)
Niech ![]() będzie otwarty i wypukły, zaś
będzie otwarty i wypukły, zaś
![]() będzie wklęsła (wypukła) i różniczkowalna
w punkcie
będzie wklęsła (wypukła) i różniczkowalna
w punkcie ![]() , który spełnia warunki
, który spełnia warunki
| (9.11) |
gdzie ![]() ,
, ![]() . Wtedy punkt
. Wtedy punkt ![]() jest punktem
globalnego warunkowego maksimum (minimum) funkcji
jest punktem
globalnego warunkowego maksimum (minimum) funkcji ![]() przy warunkach
(ograniczeniach) (9.11)
przy warunkach
(ograniczeniach) (9.11) ![]()
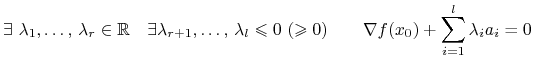 |
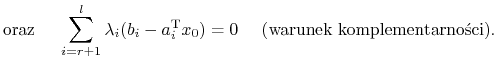 |
Uwaga 9.4
Podane tu sformułowanie twierdzenia Karusha-Kuhna-Tuckera nie jest
najogólniejszym możliwym jego sformułowaniem w kategorii wypukłej.
(I poza tym to twierdzenie istnieje też w innych kategoriach –
patrz Wykłady XIII i XIV.)
We Francji np przyszłych inżynierów uczy się takiej jego wersji,
w której zamiast ograniczeń liniowych (9.11) występują
dużo bardziej ogólne ograniczenia dawane funkcjami wypukłymi
(wklęsłymi), gdy ekstremalizowana funkcja ![]() jest wklęsła
(wypukła), porównaj np [25], s. 276. W związku
z tym twierdzenie to jest we Francji również nazywane
twierdzeniem o punkcie siodłowym.26Ściśle biorąc,
najbliższe oryginalnym pracom Karusha i Kuhna
jest wklęsła
(wypukła), porównaj np [25], s. 276. W związku
z tym twierdzenie to jest we Francji również nazywane
twierdzeniem o punkcie siodłowym.26Ściśle biorąc,
najbliższe oryginalnym pracom Karusha i Kuhna![]() Tuckera jest w
książce [25] Twierdzenie 3 na stronie 266, które jednak
nie jest tam nazwane KT, ani tym bardziej K-KT. Twierdzenie
o punkcie siodłowym na stronie 276 jest z niego wnioskiem, czy też
jednym z wniosków. W [25] w ogóle nie występuje nazwisko
Karush. Jednakże dla naszych potrzeb ograniczenia liniowe (typu
równościowego i nierównościowego) są zupełnie wystarczające.
Tuckera jest w
książce [25] Twierdzenie 3 na stronie 266, które jednak
nie jest tam nazwane KT, ani tym bardziej K-KT. Twierdzenie
o punkcie siodłowym na stronie 276 jest z niego wnioskiem, czy też
jednym z wniosków. W [25] w ogóle nie występuje nazwisko
Karush. Jednakże dla naszych potrzeb ograniczenia liniowe (typu
równościowego i nierównościowego) są zupełnie wystarczające.
Uwaga 9.5
Jeszcze z innej strony problematykę `K-KT' naświetla klasyczny podręcznik
[17]. W rozdziale `First-Order Necessary Conditions' formułuje on,
na stronach 314–315, warunki konieczne warunkowego minimum/maksimum
(zależnie, czy funkcję celu chcemy minimalizować, czy maksymalizować), i
nazywa je `Kuhn-Tucker Conditions'. Nazwisko Karush i tam się nie pojawia.
Jest to kwintesencja rezultatów Karusha i Kuhna![]() Tuckera, tak, jak
je znamy z wersji upublicznionej w [12]. (Żadnego innego dojścia
do tekstów źródłowych [11] i [14] nie mamy.) Po warunkach
koniecznych pierwszego rzędu pojawiają się w [17] jeszcze warunki
dostateczne drugiego rzędu (!). Książka bardzo godna
polecenia, napisana w solidnym anglosaskim stylu.
Tuckera, tak, jak
je znamy z wersji upublicznionej w [12]. (Żadnego innego dojścia
do tekstów źródłowych [11] i [14] nie mamy.) Po warunkach
koniecznych pierwszego rzędu pojawiają się w [17] jeszcze warunki
dostateczne drugiego rzędu (!). Książka bardzo godna
polecenia, napisana w solidnym anglosaskim stylu.
Jak już powiedziano, Twierdzenie 9.2 będziemy stosować w analizie portfelowej. Jednak dobrą rozgrzewką jest następujące zagadnienie, które też (m. in.) może być atakowane przy pomocy twierdzenia Karusha-Kuhna-Tuckera.
Ćwiczenie 9.5
Znaleźć wielomian(y) ![]() (
(![]() ) najlepiej
przybliżający(e) w normie
) najlepiej
przybliżający(e) w normie ![]() funkcję
funkcję ![]() na przedziale
na przedziale ![]() .
.
Chwytamy nieznany wielomian (na przykład) w pięciu węzłach:
![]() i postulujemy, by w tych
węzłach był on odległy od funkcji
i postulujemy, by w tych
węzłach był on odległy od funkcji ![]() o nie więcej niż
o nie więcej niż ![]() .
To znaczy postulujemy, by
.
To znaczy postulujemy, by
Każdą z funkcji ![]() na
na ![]() raz traktujemy
jako wklęsłą, raz jako wypukłą. Szukamy ich maksimów i minimów na
zbiorze opisanym pięcioma nierównościami modułowymi, albo dziesięcioma
nierównościami bezmodułowymi jak w Twierdzeniu 9.2. Komputer powinien
pomóc w przeczesaniu ogromu możliwości tutaj. Spodziewamy się następującej
odpowiedzi …
raz traktujemy
jako wklęsłą, raz jako wypukłą. Szukamy ich maksimów i minimów na
zbiorze opisanym pięcioma nierównościami modułowymi, albo dziesięcioma
nierównościami bezmodułowymi jak w Twierdzeniu 9.2. Komputer powinien
pomóc w przeczesaniu ogromu możliwości tutaj. Spodziewamy się następującej
odpowiedzi …
Pod następnym kliknięciem wyświetli się wszystkich 10 nierówności
bezmodułowych, czyli przecięcie 10 półprzestrzeni domkniętych w ![]() :
:
Podejrzenie zasadza się w tym, że to przecięcie jest jednym
punktem ![]() .
.