Zagadnienia

1.1 Rynek finansowy
1.2 Giełdy
- 1.2.1 Akcje
- 1.2.2 Obligacje
1.3 Ćwiczenia – Plany spłaty długów: metoda amortyzacji

1. Rynek kapitałowy, wiadomości wstępne

Liczba godzin 2.
Zakres materiału:
Giełda na przykładzie GPW. Uczestnicy rynku: instytucje finansowe, biura maklerskie, skarb państwa. Rynek OTC. Rodzaje instrumentów finansowych. Korzyści dla emitenta oraz dla właścicieli akcji i obligacji.

1.1. Rynek finansowy

Rynkiem finansowym (Financial Market) nazywamy rynek, na którym towarami są instrumenty finansowe. Opisując rynek finansowy, zazwyczaj bierze się pod uwagę pewne jego cechy, stanowiące podstawę klasyfikacji na różne kategorie. Najczęściej występującymi kryteriami są: A. typy instrumentów finansowych, B. horyzont czasowy, C. forma sprzedaży, D. forma organizacji rynku. Poniżej przedstawiamy schematy ogólne podziałów rynku finansowego w zależności od wybranej cechy.

A. PODZIAŁ RYNKU FINANSOWEGO ZE WZGLĘDU NA INSTRUMENTY:

$\bullet$ Rynek pieniężny (Money Market):

– transakcje krótkoterminowe (do jednego roku),
– instrumenty finansowe o dużej płynności:
1. bony skarbowe, bony komercyjne,
2. certyfikaty depozytowe,
3. czeki,
4. weksle,
5. umowy typu REPO¹Repurchase agreement – transakcja sprzedaży z obietnicą odkupienia po ustalonej cenie i w ustalonym terminie. .

$\bullet$ Rynek kapitałowy (Capital Market):

– instrumenty finansowe o charakterze własnościowym lub wierzycielskim:
1. akcje,
2. obligacje.

$\bullet$ Rynek walutowy (Forex):

– kupno i sprzedaż walut.

$\bullet$ Rynek instrumentów pochodnych (Derivatives Market):

– kontrakty pochodne:
1. futures,
2. opcje,
3. jednostki indeksowe itp.

B. PODZIAŁ RYNKU FINANSOWEGO ZE WZGLĘDU NA HORYZONT CZASOWY:

$\bullet$ Rynek natychmiastowy zwany też gotówkowym (Spot Market):

– wymiana towarów, tzn. rozliczenie kontraktu, następuje w czasie do dwóch lub trzech dni od chwili zawarcia kontraktu.

$\bullet$ Rynek terminowy (Forward Market):

– od chwili zawarcia kontraktu do momentu dostarczenia towaru, rozliczenia kontraktu, może upłynąć kilka lat.

C. PODZIAŁ RYNKU FINANSOWEGO ZE WZGLĘDU NA FORMĘ SPRZEDAŻY:

$\bullet$ Rynek pierwotny (Primary Market):

– rynek, na którym emitenci nowych instrumentów finansowych, dopiero co wyemitowanych, sprzedają je za pośrednictwem instytucji finansowych.

$\bullet$ Rynek wtórny (Secondary Market):

– rynek, na którym następuje dalszy obrót instrumentami finansowymi.

D. PODZIAŁ RYNKU FINANSOWEGO ZE WZGLĘDU NA FORMĘ ORGANIZACJI:

$\bullet$ Rynek publiczny:

– giełdy (Stock Exchange),
– regulowany rynek pozagiełdowy (np. BondSpot S.A w Warszawie (dawniej CTO²Centralna Tabela Ofert.)).

$\bullet$ Rynek prywatny (nieformalny):

– np. rynek międzybankowy.

Istotną rolę w funkcjonowaniu rynku odgrywają jego uczestnicy: czyli inwestorzy, wśród których można wyodrębnić kilka różnych grup, oraz pośrednicy.

Uczestnicy rynku:

$\bullet$ inwestorzy indywidualni;
$\bullet$ inwestorzy instytucjonalni:
1. – banki,
2. – fundusze emerytalne,
3. – zakłady ubezpieczeniowe,
4. – fundusze powiernicze *),
5. – inne instytucje finansowe.
$\bullet$ pośrednicy:
1. – maklerzy (biura maklerskie – brokers).

*)Na rynku finansowym spotykamy fundusze powiernicze dwojakiego rodzaju: otwarte i zamknięte. Fundusz otwarty emituje jednostki uczestnictwa. Wartość takiej jednostki wyznacza się jako iloraz wartości netto aktywów funduszu do liczby wydanych jednostek. Zysk uczestnika jest związany ze wzrostem wartości jednostki uczestnictwa. Fundusz zamknięty emituje akcje lub certyfikaty inwestycyjne. Uczestnik posiadający akcje funduszu otrzymuje dywidendę. Natomiast certyfikaty są odkupywane przez fundusz po cenie wyznaczonej tak, jak dla jednostek uczestnictwa.

1.2. Giełdy

Giełdy stanowią specyficzną formę wymiany towarów i zawierania transakcji. W zależności od rodzaju towarów wyróżnia się:
– giełdy towarowe (np. energii elektrycznej, produktów rolnych, surowców itp.),
– giełdy terminowe,
– giełdy papierów wartościowych.

Funkcjonowanie giełdy papierów wartościowych opiszemy na przykładzie Giełdy Papierów Wartościowych w Warszawie, gdzie notowane są następujące papiery wartościowe: akcje, prawa do akcji, prawa poboru, obligacje, certyfikaty inwestycyjne oraz instrumenty pochodne: futures, opcje, warranty i jednostki indeksowe. Zacznijmy od omówienia pokrótce podstawowych kontraktów finansowych, będących przedmiotem obrotu giełdowego, czyli akcji i obligacji.

1.2.1. Akcje

Akcja (stock, share), to dokument stwierdzający udział jej posiadacza, czyli akcjonariusza, w majątku spółki akcyjnej. Akcjonariusz ma zapewnione:
$\bullet$ prawo do dywidend;
$\bullet$ prawo do uczestnictwa w walnym zgromadzeniu akcjonariuszy;
$\bullet$ prawo do udziału w majątku spółki w przypadku jej likwidacji.

Akcje dzielimy na zwykłe i uprzywilejowane. Uprzywilejowanie zazwyczaj dotyczy:
$\bullet$ głosu na zebraniu akcjonariuszy,
$\bullet$ pierwszeństwa w wypłacaniu dywidendy,
$\bullet$ pierwszeństwa w podziale majątku spółki w przypadku jej likwidacji.

Na giełdzie inwestor może zakupić akcje dopuszczone do obrotu giełdowego, sprzedać posiadane akcje i dokonać krótkiej sprzedaży akcji (patrz. § 9.1.2) .

1.2.2. Obligacje

Obligacja, to papier wartościowy poświadczający wierzytelność na określoną sumę. Emisja obligacji nastepuje seriami, przy czym w jednej serii wszystkie obligacje mają tę samą wartość nominalną, ten sam termin wykupu i ten sam sposób naliczania odsetek (tzw. kupony). Z punktu widzenia modelowania ważne jest, czy obligacja ma stałe czy zmienne oprocentowanie oraz kto jest jej emitentem.

Obligacje o stałym oprocentowaniu dzielą się na:
$\bullet$ kuponowe;
na giełdzie warszawskiej są w obrocie: dwudziestoletnie – WSmmrr, dziesięcioletnie – DSmmrr, pięcioletnie – SPmmrr i PSmmrr³rr i mm to dwie ostatnie cyfry roku i numer miesiąca wykupu..
$\bullet$ zerokuponowe (bezodsetkowe);
na giełdzie warszawskiej są w obrocie dwuletnie OKmmrr.

Obligacje o zmiennym oprocentowaniu dzielą się na:
$\bullet$ floating, adjustable – wysokość oprocentowania jest ustalana na początku okresu oprocentowania;
na giełdzie warszawskiej są w obrocie: WZmmrr (wieloletnie), DZmmrr (dziesięcioletnie) i TZmmrr (trzyletnie).
$\bullet$ indeksowane – wysokość oprocentowania jest ustalana na koniec okresu oprocentowania, np. w zależności od wskaźnika inflacji.

Uwaga. W sierpniu 2004 roku Ministerstwo Finansów wyemitowało indeksowane obligacje skarbowe o nazwie skróconej IZ0816 i terminie wykupu w dniu 24 sierpnia 2016 roku, które zostały dopuszczone do obrotu giełdowego. Ich oprocentowanie jest stałe i wynosi 3% w skali rocznej. Natomiast wartość nominalna jest zmienna i podlega comiesięcznej indeksacji w oparciu o miesięczny wskaźnik cen towarów i usług konsumpcyjnych GUS. Odsetki (kupony), od wartości nominalnej zindeksowanej na dzień wypłaty, wypłacane są raz w roku (24 sierpnia) . W związku z powyższym kwoty odsetek są zmienne.

1.3. Ćwiczenia – Plany spłaty długów: metoda amortyzacji

Na ćwiczeniach zostanie omówiona podstawowa metoda spłaty kredytu zwana metodą amortyzacji.

Metoda amortyzacji opiera się na podziale czasu życia kredytu (długu) na okresy odsetkowe (na ogół równe). Odsetki nalicza się na koniec każdego okresu na podstawie zadłużenia z początku okresu. Przepływy gotówki (spłaty, raty, kupony itp.) w trakcie okresu są kumulowane i dlatego zazwyczaj odbywają się tylko na końcu okresu.

W każdej zapłaconej racie wyodrębnia się dwie kwoty – spłacającą kapitał i spłacającą odsetki. Zarobione przez pożyczkodawcę odsetki podlegają opodatkowaniu. Jeśli, w którymś okresie nie następuje przepływ gotówki lub nie wystarcza on na pokrycie odsetek, to powiększa się kwota zadłużenia (saldo długu). Wówczas mamy do czynienia z amortyzacją negatywną.

Okresy odsetkowe, stopy zwrotu, wielkości spłat mogą być, ale nie muszą,ustalone w momencie zawarcia umowy. Na przykład według US-rule okresy odsetkowe wyznaczane są przez spłaty kredytobiorcy. Jeśli suma wpłat w danym okresie przewyższy narosłe odsetki, okres ten zostaje uznany za zakończony.
Schemat powyższy naszkicowany jest oczywiście bardzo ogólnie.

Na konkretnym przykładzie, prześledzimy teraz jak wygląda plan spłaty kredytu zgodnie z metodą amortyzacji. Ograniczymy się do kredytu z jednorazową wypłatą bez prowizji i kosztów manipulacyjnych.
Przyjmijmy następujące oznaczenia:
$K$ – wysokość zaciągniętego kredytu,
$n$ – liczba okresów, na które podzielono czas życia kredytu,
$r_{i}$ – stopa procentowa w $i$ -tym okresie, $i=1,2,\dots n$ ,
$O_{i}$ – odsetki naliczone w $i$ -tym okresie, $i=1,2,\dots n$ ,
$CF_{i}$ – przepływ gotówki na koniec $i$ -tego okresu, $i=1,2,\dots n$ ,
$T_{i}$ – rata kapitałowa na koniec $i$ -tego okresu, $i=1,2,\dots n$ ,
$S_{i}$ – stan zadłużenia w $i$ -tym okresie, $i=1,2,\dots n+1$ , $S_{1}=K$ , $S_{{n+1}}=0$ .
Zakładamy, że wszystkie salda $S_{i}$ i stopy $r_{i}$ są nieujemne.

Wysokość odsetek wyznaczona jest przez stan zadłużenia i stopę procentową

$O_{i}=r_{i}\cdot S_{i}.$

Zazwyczaj zaokrągla się je do dwóch miejsc dziesiętnych czyli dla kredytów denominowanych w złotych, do jednego grosza.

Zmiana stanu zadłużenia zależy od przepływu gotówki i od kwoty odsetek

$S_{{i+1}}=S_{i}+O_{i}-CF_{i}.$

Zauważmy, że z warunku nieujemności $S_{{i+1}}$ wynika następujące oszacowanie dla $CF_{i}$

$CF_{i}\leq S_{i}+O_{i}.$

Ponadto, jeśli zsumujemy powyższe równości po wszystkich $i$ , to otrzymamy, że suma płatności jest równa kwocie kredytu powiększonej o sumę naliczonych odsetek.

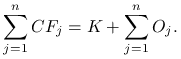$\sum _{{j=1}}^{n}CF_{j}=K+\sum _{{j=1}}^{n}O_{j}.$

Rata kapitałowa stanowi część przepływu gotówki. Gdy wszystkie spłaty $CF_{i}$ wystarczają na pokrycie aktualnych odsetek $O_{i}$ , to

$T_{i}=CF_{i}-O_{i}.$

W przeciwnym przypadku, gdy niektóre $CF_{i}$ są mniejsze od $O_{i}$ , to niespłacone części odsetek są pokrywane z następnych spłat. Ogólnie, wielkość rat opisuje następujący wzór:

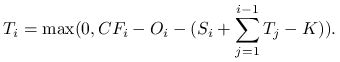$T_{i}=\max(0,CF_{i}-O_{i}-(S_{i}+\sum _{{j=1}}^{{i-1}}T_{j}-K)).$

Sprawdźmy, że zgodnie z nazwą, raty kapitałowe ,,spłacają” kredyt.

Ćwiczenie 1.1

Pokazać, że suma rat kapitałowych $T_{i}$ jest równa kwocie kredytu $K$

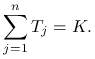$\sum _{{j=1}}^{n}T_{j}=K.$

Rozwiązanie.
Najpierw pokażemy, że suma rat $T_{i}$ nie przewyższa kwoty kredytu, tzn. że dla $i=1,2,\dots,n$

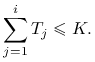$\sum _{{j=1}}^{i}T_{j}\leq K.$

Skorzystamy z zasady indukcji matematycznej. Dla $i=1$ teza jest oczywista

$T_{1}=\max(0,CF_{1}-O_{1})=\max(0,K-S_{2})\leq K.$

Załóżmy, że dla $i-1$ oszacowanie zostało udowodnione. Mamy

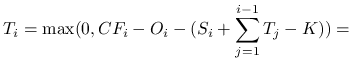$T_{i}=\max(0,CF_{i}-O_{i}-(S_{i}+\sum _{{j=1}}^{{i-1}}T_{j}-K))=$

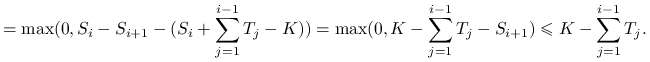$=\max(0,S_{i}-S_{{i+1}}-(S_{i}+\sum _{{j=1}}^{{i-1}}T_{j}-K))=\max(0,K-\sum _{{j=1}}^{{i-1}}T_{j}-S_{{i+1}})\leq K-\sum _{{j=1}}^{{i-1}}T_{j}.$

Po przeniesieniu sumy na lewą stronę otrzymujemy tezę indukcyjną.

Aby zakończyć dowód, należy zauważyć, że $S_{{n+1}}=0$ . Zatem na mocy udowodnionej już nierówności otrzymujemy

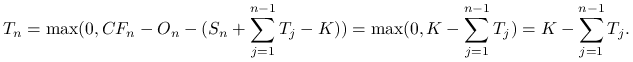$T_{n}=\max(0,CF_{n}-O_{n}-(S_{n}+\sum _{{j=1}}^{{n-1}}T_{j}-K))=\max(0,K-\sum _{{j=1}}^{{n-1}}T_{j})=K-\sum _{{j=1}}^{{n-1}}T_{j}.$

Omówione powyżej wielkości wygodnie jest przedstawiać w postaci tabeli zwanej schematem amortyzacji kredytu:

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
$i$	$S_{i}$	$r_{i}$	$O_{i}$	$T_{i}$	$CF_{i}$
$suma$			$\sum O_{i}$	$\sum T_{i}$	$\sum CF_{i}$

Ćwiczenie 1.2

Wyznaczyć schematy amortyzacji dla kredytu o:
kwocie 1000 zł,
czasie trwania – 4 lata,
okresie odsetkowym – 1 rok,
stopie procentowej stałej 10%,
wypłacie jednorazowej (w jednej transzy),
dla następujących sposobów spłaty kapitału i odsetek:
1. jednorazowa spłata kapitału i odsetek po 4 latach,
2. jednorazowa spłata kapitału po 4 latach i odsetki płatne po każdym okresie,
3. równe raty kapitałowe i odsetki płatne po każdym okresie,
4. równe spłaty ,czyli rata kapitałowa + odsetki = const.

Odpowiedź.

1. Jednorazowa spłata kapitału i odsetek po 4 latach.

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
$1$	$1000$	$0,1$	$100$	$0$	$0$
$2$	$1100$	$0,1$	$110$	$0$	$0$
$3$	$1210$	$0,1$	$121$	$0$	$0$
$4$	$1331$	$0,1$	$133,1$	$1000$	$1464,1$
$suma$			$464,1$	$1000$	$1464,1$

2. Jednorazowa spłata kapitału po 4 latach i odsetki płatne po każdym okresie.

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
$1$	$1000$	$0,1$	$100$	$0$	$100$
$2$	$1000$	$0,1$	$100$	$0$	$100$
$3$	$1000$	$0,1$	$100$	$0$	$100$
$4$	$1000$	$0,1$	$100$	$1000$	$1100$
$suma$			$400$	$1000$	$1400$

3. Równe raty kapitałowe i odsetki płatne po każdym okresie.

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
$1$	$1000$	$0,1$	$100$	$250$	$350$
$2$	$750$	$0,1$	$75$	$250$	$325$
$3$	$500$	$0,1$	$50$	$250$	$300$
$4$	$250$	$0,1$	$25$	$250$	$275$
$suma$			$250$	$1000$	$1250$

4. Równe spłaty.

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
1	1000	0,1	100	215,47	315,47
2	784,53	0,1	78,45	237,02	315,47
3	547,51	0,1	54,75	260,72	315,47
4	286,79	0,1	28,68	286,79	315,47
suma			261,88	1000	1261,88

Ćwiczenie 1.3

Opracować schemat amortyzacji w przypadku rocznego kredytu w wysokości 10 000 zł, spłacanego w równych ratach płatnych na koniec każdego z czterech kwartałów, przy stopie procentowej nominalnej $24\%$ (stopę kwartalną wyznaczamy zgodnie z zasadą równych miesięcy).

Rozwiązanie. Mamy $K=10000$ , $n=4$ , $r_{1}=r_{2}=r_{3}=r_{4}=0.24/4=0.06$ , $\; CF_{1}=CF_{2}=CF_{3}=CF_{4}\pm\varepsilon$ , gdzie $\varepsilon$ jest resztą wynikającą z zaokrągleń ( $0\leq\varepsilon<0,01\cdot\frac{n}{2}$ ). $CF_{1}$ wyznaczamy ze wzoru

$CF_{1}=K\cdot\frac{r(1+r)^{n}}{(1+r)^{n}-1},$

gdzie $r=r_{i}=0,06$ , a $n=4$ . Po zaokrągleniu otrzymujemy $CF_{1}=2885,91$ zł. Tyle samo wynoszą kolejne dwie spłaty. Ostatnią spłatę należy powiększyć o 2 grosze. Ponieważ spłaty przewyższają odsetki, to raty kapitałowe wyznaczamy ze wzoru

$T_{i}=CF_{i}-O_{i}.$

Odpowiedź.

kwartał	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
1	10000	0,06	600	2285,91	2885,91
2	7714,09	0,06	462,85	2423,06	2885,91
3	5291,03	0,06	317,46	2568,45	2885,91
4	2722,58	0,06	163,35	2722,58	2885,93
suma			1543,66	10000	11543,66

Ćwiczenie 1.4

Sporządzić schemat amortyzacji rocznego długu w wysokości 10 000 zł, spłacanego w czterech równych ratach kapitałowych przy oprocentowaniu zmiennym. W pierwszym półroczu oprocentowanie nominalne wynosiło 20%, a w drugim 24% (stopy kwartalne wyznaczono zgodnie z zasadą równych miesięcy).

Rozwiązanie. Mamy $K=10000$ , $n=4$ , $r_{1}=r_{2}=0,2/4=0,05$ , $r_{3}=r_{4}=0.24/4=0.06$ , $\; T_{1}=T_{2}=T_{3}=T_{4}=K/4=2500$ . Spłaty wyznaczamy jako sumy rat kapitałowych i odsetek

$CF_{i}=T_{i}+O_{i}.$

Odpowiedź.

kwartał	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
1	10000	0,05	500	2500	3000
2	7500	0,05	375	2500	2875
3	5000	0,06	300	2500	2800
4	2500	0,06	150	2500	2650
suma			1325	10000	11325

Ćwiczenie 1.5

Klient zaciągnął na 12 miesięcy kredyt w wysokości 1000 zł, przy nominalnej stopie procentowej 12% . Wiemy, że na koniec 3 miesiąca klient zapłacił 200 zł, a na koniec 8 miesiąca 300 zł. Obliczyć, ile ( zgodnie z zasadą równych miesięcy ) klient musi zapłacić na koniec 12 miesiąca oraz ile wyniosą raty kapitałowe:
1. przy miesięcznej kapitalizacji odsetek,
2. stosując US-rule.

Rozwiązanie.
1. Mamy

$K=1000,\;\;\; n=12,\;\;\; r_{1}=\dots=r_{{12}}=0{,}12/12=0{,}01,\;\;\; CF_{3}=200,\;\;\; CF_{8}=300.$

Szukamy $CF_{{12}}$ . Pozostałe $CF_{i}$ są zerowe.

Salda $S_{i}$ wyznaczamy w następujący sposób

$S_{1}=K=1000,$

$S_{{i+1}}=S_{i}+O_{i}-CF_{i},\;\;\mbox{ dla }i=1,\dots 11.$

Szukane $CF_{{12}}$ otrzymujemy z warunku

$0=S_{{12}}+O_{{12}}-CF_{{12}}.$

Raty kapitałowe są spłacane w 3, 8 i 12 miesiącu. Wynoszą one

$T_{3}=CF_{3}-O_{1}-O_{2}-O_{3},$

$T_{8}=CF_{8}-O_{4}-O_{5}-O_{6}-O_{7}-O_{8},$

$T_{{12}}=CF_{{12}}-O_{9}-O_{{10}}-O_{{11}}-O_{{12}}.$

Co daje następujący schemat amortyzacji:

miesiąc	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
1	1000	0,01	10	0	0
2	1010	0,01	10,1	0	0
3	1020,1	0,01	10,2	169,7	200
4	830,3	0,01	8,3	0	0
5	838,6	0,01	8,39	0	0
6	846,99	0,01	8,47	0	0
7	855,46	0,01	8,55	0	0
8	864,01	0,01	8,64	257,65	300
9	572,65	0,01	5,73	0	0
10	578,38	0,01	5,78	0	0
11	584,16	0,01	5,84	0	0
12	590	0,01	5,9	572,65	595,9
suma			95,9	1000	1095,9

2. Mamy

$K=1000,\;\;\; n=3,\;\;\; r_{1}=0{,}12/4=0{,}03,\;\;\; r_{2}=0{,}12\cdot 5/12=0{,}05,\;\;\; r_{3}=0{,}12/3=0{,}04,$

$CF_{1}=200,\;\;\; CF_{2}=300.$

Szukamy $CF_{3}$ .

Otrzymujemy następujący schemat amortyzacji:

okres	zadłużenie	stopa %	odsetki	rata kapitałowa	spłata
1	1000	0,03	30	170	200
2	830	0,05	41,5	258,5	300
3	571,5	0,04	22,86	571,5	594,36
suma			94,36	1000	1094,36

Odpowiedź. Przy miesięcznej kapitalizacji odsetek ostatnia wpłata wynosi 595,90 zł, a zgodnie z US-rule 594,36 zł. Jak widać, przy tej samej stopie nominalnej dłuższe okresy kapitalizacji zmniejszają koszt kredytu. W obu przypadkach mamy trzy raty kapitałowe, które wynoszą odpowiednio 169,70 zł, 257,65 zł i 572,65 zł oraz 170 zł, 258,50 zł i 571,50 zł.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Rynki kapitałowe (Matematyka finansowa I)

Zagadnienia

1. Rynek kapitałowy, wiadomości wstępne

1.1. Rynek finansowy

1.2. Giełdy

1.2.1. Akcje

1.2.2. Obligacje

1.3. Ćwiczenia – Plany spłaty długów: metoda amortyzacji

Ćwiczenie 1.1

Ćwiczenie 1.2

Ćwiczenie 1.3

Ćwiczenie 1.4

Ćwiczenie 1.5