Zagadnienia

10.1 Wyznaczanie kursu jednolitego
10.2 Notowania ciągłe
- 10.2.1 Arkusz zleceń
10.3 Ćwiczenia

10. Giełda. Rynek akcji – cd

10.1. Wyznaczanie kursu jednolitego

Kurs jednolity, kurs otwarcia i kurs zamknięcia wyznacza się w drodze przetargu (aukcji). Najpierw zbiera się zlecenia kupna i sprzedaży, a potem wyznacza kurs $k_{j}$ , po którym są zawierane transakcje. Oczywiście nie wszystkie zgłoszone zlecenia można zrealizować. Zlecenia kupna muszą mieć limit ceny nie mniejszy niż $k_{j}$ , a zlecenia sprzedaży – nie większy. Ponadto liczba sprzedanych papierów musi być równa liczbie kupionych. W przepisach prawnych podkreśla się, że $k_{j}$ ma maksymalizować wolumen obrotu, czyli liczbę papierów w zrealizowanych transakcjach i minimalizować nadwyżkę papierów spełniających limit ceny. W modelowaniu aukcji wygodniej jest przyjąć, że podstawowym warunkiem jest zrównoważenie rynku.

Wszystkie zlecenia kupna z limitem ceny wyższym oraz wszystkie zlecenia sprzedaży z limitem ceny niższym od $k_{j}$ muszą być zrealizowane. Zlecenia kupna z limitem ceny niższym oraz zlecenia sprzedaży z limitem ceny wyższym pozostają niezrealizowane. Natomiast zlecenia po kursie $k_{j}$ mogą być zrealizowane częściowo lub wcale.

Niech $K$ oznacza liczbę papierów w zleceniach kupna z limitem nie mniejszym niż $k_{j}$ , a $S$ liczbę papierów w zleceniach sprzedaży z limitem nie większym. Biorąc pod uwagę, że liczby zrealizowanych zleceń kupna i sprzedaży są sobie równe, zrealizowanych zostanie $\min(K,S)$ transakcji, a spośród zleceń spełniających limit ceny, $(K-S)^{+}$ ofert kupna albo $(S-K)^{+}$ ofert sprzedaży zostanie niezrealizowanych.

To, które zlecenia o limicie ceny równym $k_{j}$ zostaną zrealizowane, jest określone przez dodatkowe przepisy. W systemie WARSET, stosowanym na GPW w Warszawie od 17.11.2000, pierwszeństwo mają zlecenia złożone wcześniej. Poprzednio dokonywano proporcjonalnej redukcji zleceń. W modelowaniu (np. Double Auction Model) dopuszcza się wybór losowy.

10.1.1. Kurs równowagi

Oznaczmy przez $K_{k}$ i $S_{k}$ liczbę zleceń kupna i sprzedaży z limitem ceny $k$ , a przez $S^{+}_{k}$ , $K^{+}_{k}$ , $S^{-}_{k}$ i $K^{-}_{k}$ liczby ofert sprzedaży i kupna z limitem większym lub mniejszym od $k$ .

$S^{+}_{k}=\sum _{{p>k}}S_{p},\;\;\; K^{+}_{k}=\sum _{{p>k}}K_{p},$

$S^{-}_{k}=\sum _{{p<k}}S_{p},\;\;\; K^{-}_{k}=\sum _{{p<k}}K_{p}.$

Definicja 10.1

Kurs $k$ nazywamy kursem równowagi, gdy

$\sum _{{p\leq k}}S_{p}=S_{k}+S^{-}_{k}\geq K^{+}_{k}=\sum _{{p>k}}K_{p}$

(wszystkie oferty kupna po cenie wyższej niż $k$ mogą być zrealizowane) i

$\sum _{{p\geq k}}K_{p}=K^{+}_{k}+K_{k}\geq S^{-}_{k}=\sum _{{p<k}}S_{p}$

(wszystkie oferty sprzedaży po cenie niższej niż $k$ mogą być zrealizowane).

Oznaczmy przez $M$ zbiór kursów równowagi. Załóżmy, że łącznie zostały złożone oferty kupna $m$ i sprzedaży $n$ akcji, $n,m\geq 1$ .

$m=\sum _{{p}}K_{p},\;\;\; n=\sum _{{p}}S_{p}$

Okazuje się, że zbiór kursów równowagi jest domkniętym przedziałem lub punktem. Rzeczywiście: Ustawiamy $n+m$ limitów w ciąg rosnący

$p_{1}\leq p_{2}\leq\dots\leq p_{{n+m}}.$

Twierdzenie 10.1

$M=[p_{m},p_{{m+1}}]$

Dowód.
Krok 1. $M\supset[p_{m},p_{{m+1}}]$ .
Wybierzmy dowolny punkt $k$ z przedziału $[p_{m},p_{{m+1}}]$ . Mamy następujący układ równań i nierówności

$S^{+}_{k}+S_{k}+S^{-}_{k}=n,$

$K^{+}_{k}+K_{k}+K^{-}_{k}=m,$

$S^{-}_{k}+K^{-}_{k}\leq m,$

$S^{+}_{k}+K^{+}_{k}\leq n.$

Zatem

$S^{-}_{k}\leq m-K^{-}_{k}=K^{+}_{k}+K_{k},\;\;\; K^{+}_{k}\leq n-S^{+}_{k}=S_{k}+S^{-}_{k}.$

Czyli $k$ jest kursem równowagi.

Krok 2. $k>p_{{m+1}}\Rightarrow k\not\in M$ .
Gdy $k>p_{{m+1}}$ , to

$S^{-}_{k}+K^{-}_{k}\geq m+1.$

Zatem

$S^{-}_{k}\geq m+1-K^{-}_{k}=K^{+}_{k}+K_{k}+1.$

A stąd wynika, że nie wszystkie zlecenia sprzedaży z limitem mniejszym od $k$ mogą być zrealizowane.
$k$ nie jest kursem równowagi.

Krok 3. $k<p_{{m}}\Rightarrow k\not\in M$ .
Gdy $k<p_{{m}}$ , to

$S^{+}_{k}+K^{+}_{k}\geq n+1.$

Zatem

$K^{+}_{k}\geq n+1-S^{+}_{k}=S^{-}_{k}+S_{k}+1.$

Stąd nie wszystkie zlecenia kupna z limitem większym od $k$ mogą być zrealizowane.
$k$ nie jest kursem równowagi.

W zadaniu 10.1 $m=17$ i $p_{{17}}=p_{{18}}=20$ (dokładniej $p_{{16}}=\dots=p_{{25}}=20$ ). Zatem mamy dokładnie jeden kurs równowagi 20 tzn. $M=\{ 20\}$ . Natomiast w zadaniu 10.2 mamy $m=17$ $p_{{17}}=10<20=p_{{18}}$ , zatem $M=[10,20]$ .

10.1.2. Wolumen obrotu

Wolumen obrotu przy ustalonym kursie $x$ jest to liczba transakcji, która może być zawarta po tym kursie. Ponieważ każda transakcja wymaga udziału dwóch stron – kupującego i sprzedającego, to wolumen obrotu jest równy mniejszej z dwóch liczb:
– liczby ofert kupna po cenie nie mniejszej niż $x$ ,
oraz
– liczby ofert sprzedaży po cenie nie wyższej niż $x$

$Vol(x)=\min(\sum _{{p\geq x}}K_{p},\sum _{{p\leq x}}S_{p}).$

Twierdzenie 10.2

Każdy kurs równowagi maksymalizuje wolumen obrotu

$M\subset Max(Vol).$

Dowód.
Niech $k$ kurs równowagi.

Krok 1. $x>k\Rightarrow Vol(x)\leq Vol(k)$ .

Ponieważ $x>k$ , a $k$ jest kursem równowagi, to mamy następujący układ nierówności:

$\sum _{{p\geq x}}K_{p}\leq\sum _{{p>k}}K_{p}\;\;\left\{\begin{array}[]{cccc}\leq&\sum _{{p\leq k}}S_{p}&\leq&\sum _{{p\leq x}}S_{p}\\ &&&\\ \leq&\sum _{{p\geq k}}K_{p}.&&\end{array}\right.$

Zatem

$Vol(x)=\min(\sum _{{p\geq x}}K_{p},\sum _{{p\leq x}}S_{p})=\sum _{{p\geq x}}K_{p}\leq\min(\sum _{{p\geq k}}K_{p},\sum _{{p\leq k}}S_{p})=Vol(k).$

Krok 2. $x<k\Rightarrow Vol(x)\leq Vol(k)$ .

Ponieważ $x<k$ , a $k$ jest kursem równowagi, to mamy następujący układ nierówności:

$\sum _{{p\leq x}}S_{p}\leq\sum _{{p<k}}S_{p}\;\;\left\{\begin{array}[]{cccc}\leq&\sum _{{p\geq k}}K_{p}&\leq&\sum _{{p\geq x}}K_{p}\\ &&&\\ \leq&\sum _{{p\leq k}}S_{p}.&&\end{array}\right.$

Zatem

$Vol(x)=\min(\sum _{{p\geq x}}K_{p},\sum _{{p\leq x}}S_{p})=\sum _{{p\leq x}}S_{p}\leq\min(\sum _{{p\geq k}}K_{p},\sum _{{p\leq k}}S_{p})=Vol(k).$

Wniosek 10.1

Wolumen obrotu jest stały na $M$ .

W zadaniu 10.1 maksimum wolumenu obrotu wynosi 12 i jest ono przyjmowane na zbiorze $Max(Vol)=[20,30]$ . Natomiast w zadaniu 10.2 maksimum wolumenu obrotu też wynosi 12, ale jest ono przyjmowane na zbiorze $Max(Vol)=[10,30]$ .

10.1.3. Niezrealizowane transakcje

Oznaczmy przez $NK(x)$ i $NS(x)$ odpowiednio liczbę zleceń kupna i sprzedaży spełniających limit ceny $x$ , ale niemożliwych do zrealizowania, ponieważ brakuje zleceń przeciwnego typu,

$NK(x)=(\sum _{{p\geq x}}K_{p}-\sum _{{p\leq x}}S_{p})^{+},\;\;\; NS(x)=(\sum _{{p\leq x}}S_{p}-\sum _{{p\geq x}}K_{p})^{+}.$

Powtarzając rozumowanie z dowodu twierdzenia 10.2, otrzymujemy:

Lemat 10.1

Niech $k$ kurs równowagi. Jeżeli $x>k$ , to $NK(x)=0$ i $NS(x)\geq 0$ . Natomiast jeżeli $x<k$ , to $NK(x)\geq 0$ i $NS(x)=0$ .

Oznaczmy przez $NR(x)$ liczbę wszystkich zleceń spełniających limit ceny $x$ , ale niemożliwych do zrealizowania, ponieważ brakuje zleceń przeciwnego typu,

$NR(x)=NK(x)+NS(x)=|\sum _{{p\geq x}}K_{p}-\sum _{{p\leq x}}S_{p}|.$

Okazuje się, że kursy równowagi nie muszą minimalizować $NR$ . W przykładzie pierwszym $NR(15)=2$ , podczas gdy dla kursu równowagi $k=20$ mamy $NR=8$ .

Lemat 10.2

Jeżeli kurs równowagi $r$ należy do wnętrza przedziału $M$ , to $NR(r)=0$ i $r\in Min(NR)$ . W ogólnym przypadku kurs równowagi $r$ należy do domknięcia zbioru minimów $NR$ .

Dowód.
Niech $M=[p_{m},p_{{m+1}}]$ będzie przedziałem i $p_{m}<k<p_{{m+1}}$ . Oznacza to brak zleceń z limitem $k$ . Wówczas

$\sum _{{p\leq k}}S_{p}=\sum _{{p<k}}S_{p}\leq\sum _{{p\geq k}}K_{p}=\sum _{{p>k}}K_{p}\leq\sum _{{p\leq k}}S_{p}.$

Zatem

$\sum _{{p\leq k}}S_{p}=\sum _{{p\geq k}}K_{p}\;\;\;\mbox{ i }\;\; NR(k)=0.$

Aby zakończyć dowód, wystarczy zauważyć, że dla $x>p_{{m+1}}$ (na prawo od $M$ ) funkcja $NR(x)$ jest niemalejąca, a dla $x<p_{m}$ (na lewo) nierosnąca.

Lemat 10.3

Niech $M=[p_{{m}},p_{{m+1}}]$ , gdzie $m$ liczba akcji w zleceniach kupna. Wówczas:
a) Jeżeli $k\in Max(Vol)$ i $k>p_{{m+1}}$ to $NR(k)\geq NR(p_{{m+1}})$ .
b) Jeżeli $k\in Max(Vol)$ i $k<p_{{m}}$ to $NR(k)\geq NR(p_{{m}})$ .

Dowód.
Punkt a.
Wybieramy $k_{1}$ , takie, że
i. $k>k_{1}>p_{{m+1}}$ ,
ii. nie ma zleceń sprzedaży z limitem ceny w przedziale $(p_{{m+1}},k_{1})$ .
Z i. wynikają następujące nierówności

$\sum _{{p\leq k}}S_{p}\geq\sum _{{p<k_{1}}}S_{p}>\sum _{{p\geq k_{1}}}K_{p}\geq\sum _{{p\geq k}}K_{p}.$

Z ii. wynika równość

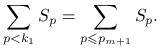$\sum _{{p<k_{1}}}S_{p}=\sum _{{p\leq p_{{m+1}}}}S_{p}.$

Zatem

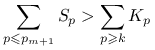$\sum _{{p\leq p_{{m+1}}}}S_{p}>\sum _{{p\geq k}}K_{p}$

oraz

$\sum _{{p\leq k}}S_{p}>\sum _{{p\geq k}}K_{p}.$

Ponieważ wolumen obrotu maksymalizuje się zarówno dla $k$ jak i dla $p_{{m+1}}$ to

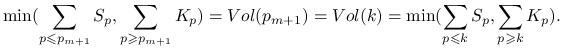$\min(\sum _{{p\leq p_{{m+1}}}}S_{p},\sum _{{p\geq p_{{m+1}}}}K_{p})=Vol(p_{{m+1}})=Vol(k)=\min(\sum _{{p\leq k}}S_{p},\sum _{{p\geq k}}K_{p}).$

Z powyższych ,,ostrych” nierówności wynika, że suma $\sum _{{p\geq k}}K_{p}$ jest mniejsza niż oba pierwsze argumenty $min$ , zatem jest równa drugiemu argumentowi pierwszego minimum

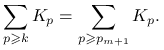$\sum _{{p\geq k}}K_{p}=\sum _{{p\geq p_{{m+1}}}}K_{p}.$

Podsumowując

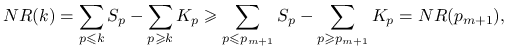$NR(k)=\sum _{{p\leq k}}S_{p}-\sum _{{p\geq k}}K_{p}\geq\sum _{{p\leq p_{{m+1}}}}S_{p}-\sum _{{p\geq p_{{m+1}}}}K_{p}=NR(p_{{m+1}}),$

co kończy dowód implikacji a. Implikację b. dowodzi się analogicznie.

Wniosek 10.2

Jeżeli zbiór kursów równowagi jest jednoelementowy, to jest on punktem brzegowym zbioru $Max(Vol)$

$p_{m}=p_{{m+1}}\Rightarrow M\subset\partial Max(Vol).$

10.1.4. Wyznaczanie kursu jednolitego

Gdy złożone zlecenia kupna i sprzedaży dopuszczają tylko jeden kurs równowagi ( $M$ jednopunktowy), to można ustalić go jako kurs jednolity, po którym zawierane są wszystkie transakcje. W przeciwnym przypadku

$M=[p_{m},p_{{m+1}}],\;\;\;\; p_{m}<p_{{m+1}},$

wybór kursu jednolitego jest bardziej skomplikowany.

Przykłady możliwych algorytmów wyboru kursu jednolitego $k_{j}$ .

1. Średnia ważona.
Ustalamy liczbę $k\in[0,1]$

$k_{j}=kp_{m}+(1-k)p_{{m+1}}.$

Ten schemat jest chętnie wykorzystywany w rozważaniach teoretycznych np. w ,,k-Double Auction Model”.

2. W zależności od kursu odniesienia.
Jako kurs jednolity wybieramy kurs równowagi najbliższy kursowi odniesienia $k_{o}$

$k_{j}=\left\{\begin{array}[]{ccc}p_{m}&\mbox{ gdy }&k_{o}\leq p_{m},\\ k_{o}&\mbox{ gdy }&p_{m}<k_{o}<p_{{m+1}},\\ p_{{m+1}}&\mbox{ gdy }&p_{{m+1}}\leq k_{o}.\end{array}\right.$

Ten algorytm daje ten sam wynik co schemat stosowany na giełdzie we Frankfurcie ([27] §11). Kurs odniesienia to zwykle ostatni kurs jednolity lub kurs ostatniej transakcji. Warto zauważyć, że jeśli ustalimy dyskretny zbiór dopuszczalnych notowań (limitów), to tak wyznaczony kurs równowagi należy do tego zbioru.

3. W zależności od liczby niezrealizowanych zleceń spełniających limit ceny i od kursu odniesienia $k_{o}$ .
Ustalamy dyskretny zbiór dopuszczalnych notowań $\Lambda$ . Wybieramy te $k\in M\cap\Lambda$ , które minimalizują liczbę niezrealizowanych zleceń spełniających limit ceny. A następnie spośród nich ten, który minimalizuje moduł różnicy kursu jednolitego i kursu odniesienia:
i. $NR(k_{j})\rightarrow min$ ,

$M_{1}=\{ k\in M\cap\Lambda:NR(k)=\min\{ NR(x):x\in M\cap\Lambda\},$

ii. $|k_{j}-k_{o}|\rightarrow min$ ,

$k_{j}\in M_{1}\;\;\;\wedge\;\;\;|k_{j}-k_{o}|=min\{|k-k_{o}|:k\in M_{1}\}.$

WARSET (system komputerowy obsługujący Giełdę Papierów Wartościowych w Warszawie) wyznacza kurs jednolity taki sam jak ostatni z podanych algorytmów.

Algorytm ten może prowadzić do innych wyników niż algorytm zamieszczony w regulaminie giełdy ([36] §136), który nakazuje maklerowi kolejno:
1. Maksymalizować wolumen obrotu.
2. Minimalizować liczbę niezrealizowanych zleceń spełniających limit ceny.
3. Minimalizować moduł różnicy kursu jednolitego i kursu odniesienia.

Z drugiej strony w ,,szczegółowych zasadach obrotu giełdowego” ([44] §VI.7) jest zapisane, że ma to być kurs równowagi. Niestety nie zawsze kurs wyznaczony zgodnie z punktami 1, 2 i 3, jest kursem równowagi (patrz zadanie 10.4).

Dlatego w opisie WARSET-u ([47]) zaproponowano wprowadzenie czwartego punktu:
4. Wyznaczyć kurs równowagi najbliższy kursowi wyznaczonemu w punkcie 3.

Zauważmy, że alternatywnym rozwiązaniem byłoby dodanie punktu 2':
2'. Spośród kursów wyznaczonych w punktach 1 i 2 wybrać kursy równowagi.

10.2. Notowania ciągłe

W czasie notowań ciągłych kupujący i sprzedający składają zlecenia, które po przekazaniu na giełdę są realizowane na bieżąco, pod warunkiem zgodności cen, lub trafiają do arkusza zleceń i oczekują ofert przeciwnych o odpowiedniej cenie, umożliwiających zawarcie transakcji. Przy realizacji zleceń obowiązują dwa priorytety: cena i czas złożenia zlecenia. Oznacza to, że w przypadku gdy czekają na realizację dwa zlecenia po identycznej cenie, jako pierwsze realizowane jest to, które zostało przekazane na giełdę wcześniej. Transakcje są zawierane po cenie zlecenia oczekującego.

10.2.1. Arkusz zleceń

Po fazie fixingu na otwarciu wszystkie niezrealizowane zlecenia, które nie zostały wycofane przez inwestorów, są umieszczane w arkuszu zleceń. Po uporządkowaniu zleceń według limitów arkusz wygląda następująco:

Limit	Kupno	Sprzedaż
…	–	…
$ls_{3}$	–	$s_{3}$
$ls_{2}$	–	$s_{2}$
$ls_{1}$	–	$s_{1}$
$lk_{1}$	$k_{1}$	-
$lk_{2}$	$k_{2}$	-
$lk_{3}$	$k_{3}$	-
…	–	…

Załóżmy, że zostało złożone nowe zlecenie sprzedaży: $s$ akcji z limitem ceny $ls$ .
$\bullet$ Jeżeli limit ceny $ls$ jest większy od najwyższego limitu kupna $lk_{1}$ , to zlecenia nie można zrealizować i zostaje ono umieszczone w całości w arkuszu zleceń.
$\bullet$ Jeżeli limit ceny $ls$ jest nie większy od najwyższego limitu kupna $lk_{1}$ , to zlecenia zostaje zrealizowane po kursie $lk_{1}$ – całkowicie, gdy $s\leq k_{1}$ , lub częściowo, gdy $s>k_{1}$ . Zrealizowane zlecenia kupna zostają usunięte z arkusza. Gdy $s>k_{1}$ , to pozostałą część zlecenia sprzedaży traktuje się jak nowe zlecenie ( $s-k_{1}$ akcji z limitem ceny $ls$ ) i powtarza powyższe kroki.

W przypadku zleceń kupna postępuje się podobnie.

10.3. Ćwiczenia

Ćwiczenie 10.1

Złożono dwa zlecenia kupna:
a) 5 akcji z limitem ceny 10 zł;
b) 12 akcji z limitem ceny 30 zł;
oraz trzy zlecenia sprzedaży:
c) 10 akcji z limitem ceny 10 zł;
d) 10 akcji z limitem ceny 20 zł;
e) 5 akcji z limitem ceny 30 zł.
Wyznaczyć kurs(y) równowagi, wolumen obrotu i liczbę niezrealizowanych transakcji spośród transakcji spełniających limit ceny. Ponadto sprawdzić, które zlecenia zostaną zrealizowane.

Rozwiązanie.
Porządkujemy zlecenia według limitu ceny.

Limit	Kupno	Sprzedaż
30	12	5
20	–	10
10	5	10
Razem	17	25

Odpowiedź.
Kurs równowagi wynosi 20 zł. Przy tym kursie zlecenia b i c zostają zrealizowane w całości, zlecenie d częściowo (tylko 2 akcje), a zlecenia a i e pozostają nie zrealizowane. Wolumen obrotu wyniósł 12 akcji. Liczba niezrealizowanych transakcji spośród transakcji spełniających limit ceny wyniosła 8 zł.

Ćwiczenie 10.2

Złożono dwa zlecenia kupna:
a) 5 akcji z limitem ceny 10 zł;
b) 12 akcji z limitem ceny 30 zł;
oraz trzy zlecenia sprzedaży:
c) 12 akcji z limitem ceny 10 zł;
d) 10 akcji z limitem ceny 20 zł;
e) 5 akcji z limitem ceny 30 zł.
Wyznaczyć zbiór kursów równowagi.

Rozwiązanie.
Porządkujemy zlecenia według limitu ceny.

Limit	Kupno	Sprzedaż
30	12	5
20	–	10
10	5	12
Razem	17	27

Otrzymujemy $m=17$ ,

$p_{1}=\dots p_{{17}}=10,\;\;\; p_{{18}}=\dots=p_{{27}}=20,\;\;\; p_{{28}}=\dots=p_{{44}}=30.$

Odpowiedź.
Zatem $M=[10,20]$ . Każdy kurs z przedziału $[10,20]$ jest kursem równowagi.

Ćwiczenie 10.3

Kurs odniesienia wynosi 120 zł, krok notowania 0.5 zł. Złożono trzy zlecenia kupna:
– 5 akcji z limitem ceny 119 zł;
– 15 akcji z limitem ceny 121 zł;
– 15 akcji z limitem ceny 122 zł;
oraz dwa zlecenia sprzedaży:
– 20 akcji z limitem ceny 118 zł oraz
– 5 akcji z limitem ceny 119 zł.
Wyznaczyć zbiór kursów równowagi.

Rozwiązanie.

Limit	Kupno	Sprzedaż	Kumulacja
122	15	–	60
121	15	–	45
119	5	5	30
118	–	20	20
Razem	35	25

Ponieważ łącznie było ofert kupna na 35 akcji, to kurs równowagi jest wyznaczony jednoznacznie i wynosi 121 zł ( $p_{{35}}=p_{{36}}=121$ ).

Odpowiedź.
Kurs równowagi jest wyznaczony jednoznacznie i wynosi 121.

Ćwiczenie 10.4

Dla tych samych zleceń co w zadaniu 10.3, wiedząc, że kurs odniesienia wynosi 120 zł a krok notowania 0.5 zł wyznaczyć kurs jednolity zgodnie z regulaminem giełdy. Sprawdzić, czy jest on kursem równowagi.

Rozwiązanie.

Limit	Kupno	Sprzedaż	Wolumen	NR
	Skumulowane
122	15	25	15	10
121.5	15	25	15	10
121	30	25	25	5
120.5	30	25	25	5
120	30	25	25	5
119.5	30	25	25	5
119	35	25	25	10
118.5	35	20	20	15
118	35	20	20	15

Zatem wolumen maksymalizują następujące kursy: 119, 119.5, 120, 120.5, 121.
Liczbę niezrealizowanych transakcji minimalizują kursy: 119.5, 120, 120.5, 121.
Spośród nich najbliższy kursowi odniesienia jest 120, który nie jest kursem równowagi.

Odpowiedź.
Kurs jednolity wyznaczony zgodnie z regulaminem giełdy wynosi 120 zł, ale nie jest on kursem równowagi.

Ćwiczenie 10.5

O godzinie 11:00 w arkuszu zleceń było 7 zleceń kupna (w zł)

limit ceny	31	31,3	31,5	31,5	31,5	31,8	31,9
liczba akcji	500	500	415	1000	2000	400	600

i 7 zleceń sprzedaży (w zł)

limit ceny	32	32,3	32,5	32,6	32,7	32,8	33
liczba akcji	19	1650	1451	3986	1200	1000	299

O godzinie 11:05 inwestor X złożył zlecenie kupna 200 akcji z limitem 31,8 zł. Między 11:00 a 12:00, oprócz jego zlecenia, złożone zostały tylko następujące zlecenia:

czas	11:10	11:20	11:30	11:35	11:45
	K	S	S	S	K
limit ceny	32,2	31,9	31,5	31,9	32,5
liczba akcji	50	400	700	200	100

Czy zlecenie inwestora X zostało zrealizowane do godziny 11:55?
Jaki był kurs ostatniej zrealizowanej przed 12:00 transakcji?

Rozwiązanie.O 11:05 najlepszy oczekujący kurs sprzedaży wynosił 32 zł, zatem zlecenie inwestora X nie mogło być zrealizowane i zostało umieszczone w arkuszu zleceń.

Zlecenie kupna z godziny 11:10 zostało zrealizowane częściowo (19 akcji), a pozostała część (31 akcji) została umieszczona w arkuszu zleceń. W efekcie zlecenie inwestora X znalazło się na 4 miejscu po następujących zleceniach kupna: 31 akcji po 32,2 zł, 600 po 31,9 zł i 400 po 31,8 zł.

Zlecenia sprzedaży z godziny 11:20 i 11:30 zostały zrealizowane całkowicie w momencie złożenia. W szczególności o 11:30 zrealizowano część zlecenia inwestora X. Zakupił on 69 akcji po kursie 31,8 zł.

Zlecenie sprzedaży z godziny 11:35 nie moglo być zrealizowane i zostało w całości umieszczone w arkuszu zleceń (jako najlepsze oczekujące zlecenie sprzedaży).

Zlecenie kupna z godziny 11:45 zostało zrealizowane całkowicie po najlepszym oczekującym kursie sprzedaży, czyli po 31,9 zł.

Odpowiedź. Wyniki do godziny 12:00 były następujące:
Zlecenie inwestora X zostało zrealizowane częściowo. Zakupił on tylko 69 akcji.
Natomiast kurs ostatniej transakcji wyniósł 31,9 zł.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Rynki kapitałowe (Matematyka finansowa I)

Zagadnienia

10. Giełda. Rynek akcji – cd

10.1. Wyznaczanie kursu jednolitego

10.1.1. Kurs równowagi

Definicja 10.1

Twierdzenie 10.1

10.1.2. Wolumen obrotu

Twierdzenie 10.2

Wniosek 10.1

10.1.3. Niezrealizowane transakcje

Lemat 10.1

Lemat 10.2

Lemat 10.3

Wniosek 10.2

10.1.4. Wyznaczanie kursu jednolitego

10.2. Notowania ciągłe

10.2.1. Arkusz zleceń

10.3. Ćwiczenia

Ćwiczenie 10.1

Ćwiczenie 10.2

Ćwiczenie 10.3

Ćwiczenie 10.4

Ćwiczenie 10.5