Zagadnienia
15. Metody stochastyczne w finansach – cd
15.1. Value at Risk – inne spojrzenie na ryzyko finansowe
15.1.1. Wprowadzenie i definicja
Value at Risk
(wartość zagrożona ryzykiem, w skrócie ![]() ) jest przykładem
miary ryzyka opartej
na nieco innej filozofii niż miary omówione w wykładzie 14. VaR, to miara,
za pomocą której nie tyle określa się,
na ile niedokładne są prognozy końcowego wyniku inwestycji,
ale uzyskuje informacje jak duże środki należy przeznaczyć na zabezpieczenie danej inwestycji, a nawet całej instytucji finansowej.
Krótko mówiąc VaR uprzedza nas, ile możemy stracić.
) jest przykładem
miary ryzyka opartej
na nieco innej filozofii niż miary omówione w wykładzie 14. VaR, to miara,
za pomocą której nie tyle określa się,
na ile niedokładne są prognozy końcowego wyniku inwestycji,
ale uzyskuje informacje jak duże środki należy przeznaczyć na zabezpieczenie danej inwestycji, a nawet całej instytucji finansowej.
Krótko mówiąc VaR uprzedza nas, ile możemy stracić.
Miary takie jak VaR wykorzystuje się m.in.:
-
 jako element kontroli, np.:
jako element kontroli, np.:
– poszczególnych departamentów i oddziałów przez zarząd banku,
– poszczególnych banków przez nadzór bankowy,
– zarządu spółki akcyjnej przez radę nadzorczą i akcjonariuszy; -
 przy ustalaniu limitów dotyczących adekwatności kapitałowej instytucji finansowych,
czyli określaniu ,,jak duże powinny być środki własne firmy, aby zabezpieczona była jej wypłacalność”;
przy ustalaniu limitów dotyczących adekwatności kapitałowej instytucji finansowych,
czyli określaniu ,,jak duże powinny być środki własne firmy, aby zabezpieczona była jej wypłacalność”; -
 przy ustalaniu wysokości depozytów wymaganych przez
izby rozrachunkowe działające na rynku
instrumentów pochodnych;
przy ustalaniu wysokości depozytów wymaganych przez
izby rozrachunkowe działające na rynku
instrumentów pochodnych;
-
 jako benchmark przy podejmowaniu decyzji inwestycyjnych, np.:
jako benchmark przy podejmowaniu decyzji inwestycyjnych, np.:
,,Ustala się pewną wartość graniczną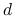 i zarządzający portfelem inwestycyjnym może tylko tak kształtować skład
portfela, aby dana miara ryzyka jej nie przekroczyła”.
i zarządzający portfelem inwestycyjnym może tylko tak kształtować skład
portfela, aby dana miara ryzyka jej nie przekroczyła”.
Ogólnie, Value at Risk to odpowiedź probabilisty na pytanie
,,ile można stracić?”. Jest to największa strata,
jaką można ponieść przy zadanym poziomie ufności ![]() .
.
Ustalmy pewien horyzont czasowy ![]() .
Niech
.
Niech ![]() będzie zmienną losową, za pomocą której modelujemy przyszły stan należności netto
danej instytucji finansowej
(pasywa minus aktywa)
albo stratę z danej inwestycji (aktualna wartość inwestycji minus jej wartość po upływie czasu
będzie zmienną losową, za pomocą której modelujemy przyszły stan należności netto
danej instytucji finansowej
(pasywa minus aktywa)
albo stratę z danej inwestycji (aktualna wartość inwestycji minus jej wartość po upływie czasu ![]() ).
Jeśli
).
Jeśli ![]() ma rozkład ciągły i jej dystybuanta jest ściśle rosnąca (np.
ma rozkład ciągły i jej dystybuanta jest ściśle rosnąca (np. ![]() ma rozkład normalny),
to
ma rozkład normalny),
to
![]() określa się w następujący sposób
określa się w następujący sposób
W przypadku ogólnym (np. gdy zmienna losowa ![]() jest dyskretna)
powyższe równanie może nie mieć rozwiązań lub może mieć ich więcej niż jedno.
Dlatego też zdefiniujemy
jest dyskretna)
powyższe równanie może nie mieć rozwiązań lub może mieć ich więcej niż jedno.
Dlatego też zdefiniujemy ![]() jako tzw. dolny kwantyl.
jako tzw. dolny kwantyl.
Definicja 15.1
Dla dowolnej zmiennej losowej ![]() i dowolnego poziomu ufności
i dowolnego poziomu ufności
![]()
Oczywiście można też definiować ![]() jako górny kwantyl
jako górny kwantyl
lub jako średnią ważoną obu kwantyli.
Kwestią otwartą pozostaje wybór właściwego poziomu ufności ![]() .
Analitycy banku J.P.Morgan, twórcy pojęcia Value at Risk, przyjmowali
.
Analitycy banku J.P.Morgan, twórcy pojęcia Value at Risk, przyjmowali ![]() ([37]).
Natomiast Komitet Bazylejski postuluje przyjęcie
([37]).
Natomiast Komitet Bazylejski postuluje przyjęcie ![]() ([5]).
Ta różnica wynika między innymi z faktu, że według analityków z banku J.P.Morgan Value at Risk miało być
narzędziem kontrolnym używanym przez zarząd banku, natomiast Komitet Bazylejski
zaproponował użycie Value at Risk w ramach nadzoru bankowego. Oczywiste jest, że nadzór zewnętrzny
jest bardziej wymagający (większe
([5]).
Ta różnica wynika między innymi z faktu, że według analityków z banku J.P.Morgan Value at Risk miało być
narzędziem kontrolnym używanym przez zarząd banku, natomiast Komitet Bazylejski
zaproponował użycie Value at Risk w ramach nadzoru bankowego. Oczywiste jest, że nadzór zewnętrzny
jest bardziej wymagający (większe ![]() oznacza większą wartość
oznacza większą wartość ![]() ).
).
Omówimy pokrótce podstawowe własności ![]() .
Zauważmy, że oba zbiory
.
Zauważmy, że oba zbiory
![]() i
i ![]() są półprostymi,
wobec tego kres górny każdego z nich jest równy kresowy dolnemu odpowiednio każdego z dopełnień. Zatem
są półprostymi,
wobec tego kres górny każdego z nich jest równy kresowy dolnemu odpowiednio każdego z dopełnień. Zatem ![]() i
i ![]() są równe odpowiednio
są równe odpowiednio
Korzystając z powyższego, udowodnimy następujący lemat.
Lemat 15.1
Dla dowolnej zmiennej losowej ![]() i dowolnego poziomu ufności
i dowolnego poziomu ufności ![]() :
:
1. ![]() ;
;
2. Jeśli ![]() jest większy od
jest większy od ![]() , to
, to ![]() ;
;
3. Jeśli ![]() jest mniejszy od
jest mniejszy od ![]() , to
, to ![]() .
.
Ponadto, gdy ![]() nie jest równy
nie jest równy ![]() , to:
, to:
4. ![]() ;
;
5. Dla dowolnego ![]() z przedziału otwartego
z przedziału otwartego ![]() ,
,![]() ;
;
6. ![]() .
.
Dowód.
Punkt 1 wynika z ciągłości prawdopodobieństwa ([21] §Twierdzenie 7).
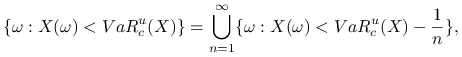 |
zatem, ponieważ ![]() , to
, to
Podobnie
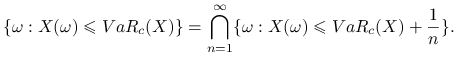 |
Ponieważ ![]() , to
, to
Punkt 2 wynika z przedstawienia ![]() jako kres dolny, a punkt 3
z przedstawienia
jako kres dolny, a punkt 3
z przedstawienia ![]() jako kres górny.
jako kres górny.
Punkt 4 wynika z nierówności z punktu 1 i z faktu, że ![]() jest mniejszy od
jest mniejszy od ![]() .
.
wobec tego wszystkie nierówności ,,![]() ” w tym wzorze są równościami.
” w tym wzorze są równościami.
Podobnie pokazuje się punkt 5:
Punkt 6 wynika z punktu 4.
15.1.2. Alokacja kapitału
Na zakończenie przeanalizujmy możliwość zastosowania Value at Risk
do wyznaczania optymalnej alokacji posiadanych środków.
Rozważymy następujący prosty przykład.
Udziałowcy Towarzystwa Ubezpieczeniowego TU SA zastanawiają się, czy zachodzi potrzeba dokapitalizowania spółki.
TU SA sprzedało szereg polis ubezpieczeniowych co może skutkowac wypłatą wysokich odszkodowań.
Jeśli kwota odszkodowań przekroczy posiadane fundusze, TU SA będzie zagrożone bankructwem.
Aby go uniknąć udziałowcy będą zmuszeni do poniesienia dodatkowych kosztów.
Z drugiej strony dokapitalizowanie też wiąże się z pewnymi kosztami. W tej sytuacji udziałowcy
muszą rozstrzygnąć, jaki jest optymalny poziom funduszy posiadanych przez TU SA.
Przyjmiemy następujące oznaczenia:![]() – wielkość odszkodowań pomniejszoną o środki posiadane przez TU SA (modelujemy ją jako zmienną losową);
– wielkość odszkodowań pomniejszoną o środki posiadane przez TU SA (modelujemy ją jako zmienną losową);![]() – kwota, którą udziałowcy chcą dokapitalizować spółkę;
– kwota, którą udziałowcy chcą dokapitalizować spółkę;![]() – koszty w zależności od
– koszty w zależności od ![]() i
i ![]() .
.
gdzie: ![]() – koszt kapitału (np. stopa procentowa),
– koszt kapitału (np. stopa procentowa), ![]() – koszty, które poniosą udziałowcy na pokrycie roszczeń
przekraczających fundusze TU SA (w przeliczeniu na 1 jednostkę monetarną). Oczywiście
– koszty, które poniosą udziałowcy na pokrycie roszczeń
przekraczających fundusze TU SA (w przeliczeniu na 1 jednostkę monetarną). Oczywiście ![]() .
.
Racjonalni akcjonariusze będą się starać zminimalizować oczekiwane koszty.
A więc wybiorą ![]() , które zminimalizuje wartość oczekiwaną relatywnej straty, czyli różnicy
, które zminimalizuje wartość oczekiwaną relatywnej straty, czyli różnicy
![]() ,
,
Pokażemy, że optymalny poziom dokapitalizowania jest równy
Value at Risk ![]() , wyznaczonemu dla poziomu ufności
, wyznaczonemu dla poziomu ufności ![]() .
.
Zauważmy, że
w odróżnieniu od straty ![]() , relatywna strata
, relatywna strata
jest ograniczona i
niezależnie od tego, jaki jest rozkład ![]() i ile wynosi
i ile wynosi ![]() ,
posiada skończoną wartość oczekiwaną, która jest funkcją ciągłą zmiennej
,
posiada skończoną wartość oczekiwaną, która jest funkcją ciągłą zmiennej ![]() . Ponadto, gdy
. Ponadto, gdy ![]() mają skończoną
wartość oczekiwaną, to
mają skończoną
wartość oczekiwaną, to ![]() i
i ![]() przyjmują minimum w tych samych punktach.
przyjmują minimum w tych samych punktach.
Twierdzenie 15.1
![]() minimalizuje wartość oczekiwaną relatywnej straty
minimalizuje wartość oczekiwaną relatywnej straty ![]() dla
dla ![]() .
Ponadto, jeśli dystrybuanta
.
Ponadto, jeśli dystrybuanta ![]() jest ściśle rosnąca w pewnym otoczeniu punktu
jest ściśle rosnąca w pewnym otoczeniu punktu
![]() , to jest to jedyne minimum. W przeciwnym wypadku
zbiór minimów
, to jest to jedyne minimum. W przeciwnym wypadku
zbiór minimów ![]() jest przedziałem domkniętym
jest przedziałem domkniętym
Dowód.
Niech ![]() i
i ![]() ,
, ![]() , będą dowolnymi liczbami rzeczywistymi. Zapiszemy różnicę relatywnych strat
za pomocą funkcji charakterystycznych
, będą dowolnymi liczbami rzeczywistymi. Zapiszemy różnicę relatywnych strat
za pomocą funkcji charakterystycznych ![]()
Zatem przyrost wartości oczekiwanej relatywnej straty wynosi
Rozważymy trzy przypadki:
A. Oba punkty leżą na prawo od ![]() ,
,
B. Oba punkty leżą na lewo od ![]() ,
,
C. Oba punkty leżą pomiędzy ![]() i
i ![]() ,
,
Przypadek A.
Na mocy lematu 5.4.1
Wobec tego
Zatem, ponieważ wartość oczekiwana nieujemnej zmiennej losowej jest nieujemna, to
W ten sposób pokazaliśmy, że funkcja ![]() jest ściśle rosnąca na półprostej
jest ściśle rosnąca na półprostej![]() .
Ale wiemy, że jest ona ciągła, zatem jest ściśle rosnąca na półprostej domkniętej
.
Ale wiemy, że jest ona ciągła, zatem jest ściśle rosnąca na półprostej domkniętej ![]() .
.
Przypadek B.
Na mocy lematu 5.4.1
Wobec tego
Zatem, ponieważ wartość oczekiwana nieujemnej zmiennej losowej jest nieujemna, to
W ten sposób pokazaliśmy, że funkcja ![]() jest ściśle malejąca na półprostej
jest ściśle malejąca na półprostej
![]() .
Z ciągłości wynika, że jest ona ściśle malejąca na półprostej domkniętej
.
Z ciągłości wynika, że jest ona ściśle malejąca na półprostej domkniętej ![]() .
.
Przypadek C.
Gdy ![]() jest mniejszy od
jest mniejszy od ![]() , to
na mocy lematu 5.4.1
, to
na mocy lematu 5.4.1
Wobec tego
Ponadto
czyli
Z powyższego wynika, że
W ten sposób pokazaliśmy, że funkcja ![]() jest stała na odcinku
jest stała na odcinku![]() .
Z ciągłości wynika, że jest ona stała na odcinku domkniętym
.
Z ciągłości wynika, że jest ona stała na odcinku domkniętym ![]() .
.
Podsumowując, gdy dystrybuanta ![]() jest ściśle monotoniczna w pewnym otoczeniu
jest ściśle monotoniczna w pewnym otoczeniu ![]() , to
, to
![]() i
i ![]() przyjmuje minimum dokładnie w jednym punkcie.
W przeciwnym przypadku każdy punkt z przedziału
przyjmuje minimum dokładnie w jednym punkcie.
W przeciwnym przypadku każdy punkt z przedziału
![]() minimalizuje
minimalizuje ![]() .
.
15.2. Teoretyczne podstawy pomiaru ryzyka dla inwestycji finansowych.
Każdą inwestycję ![]() charakteryzujemy za pomocą dwóch wielkości:
charakteryzujemy za pomocą dwóch wielkości:
wartości początkowej (nakładów) ozn. ![]()
i wartości końcowej (wypłaty, bogactwa końcowego) ozn. ![]() .
.![]() i jest znane w momencie rozpoczęcia inwestycji.
i jest znane w momencie rozpoczęcia inwestycji.![]() modelujemy jako zmienną losową określoną na pewnej przestrzeni probabilistycznej
modelujemy jako zmienną losową określoną na pewnej przestrzeni probabilistycznej
![]() .
.
W tej konwencji![]() oznacza zysk,
oznacza zysk,![]() stratę,
stratę,
a stopa zwrotu to ![]() .
.
Ponadto ze względów technicznych zakładamy, że zbiór dopuszczalnych inwestycji ![]() jest stożkiem wypukłym
jest stożkiem wypukłym
oraz zawiera inwestycję o zerowym zysku
Inwestycje ![]() z punktów i. oraz ii. będziemy oznaczać odpowiednio
z punktów i. oraz ii. będziemy oznaczać odpowiednio
![]() i
i ![]() .
.
Z punktu widzenia metodologicznego wyróżniamy dwie grupy miar ryzyka: miary dyspersji i miary monotoniczne. Osobną grupę stanowią miary efektywności, ściśle związane z ryzykiem nieosiągnięcia zakładanego poziomu zysku albo stopy zwrotu.
15.2.1. Miary dyspersji.
Miary dyspersji ostrzegają, o ile stopa zwrotu ![]() albo wypłata
albo wypłata ![]() różnią się od prognozy
(np. wartości oczekiwanej lub mediany).
Ostrzeżenie to może dotyczyć zarówno:
różnią się od prognozy
(np. wartości oczekiwanej lub mediany).
Ostrzeżenie to może dotyczyć zarówno:
1. Możliwości wystąpienia efektu niezgodnego z przewidywaniami. Nieważne, czy jest to
przykra niespodzianka, czy przyjemne zaskoczenie; ważne, że prognoza była niedokładna.
2. Możliwości poniesienia straty. Uwzględniamy tylko przykre niespodzianki.
Najbardziej popularne miary ryzyka-dyspersji to omówione na poprzednim wykładzie (patrz 14.3.1):
1. Odchylenie standardowe i wariancja.
Wyznaczamy prognozę błędu prognozy.
2. Ujemne semiodchylenie standardowe
i ujemna semiwariancja.
Są to odpowiedniki odchylenia standardowego i wariancji w przypadku drugiej interpretacji ryzyka.
3. Odchylenie przeciętne i ujemne semiodchylenie przeciętne.
Więcej przykładów i informacji o miarach dyspersji (dewiacji) czytelnik może znaleźć w pracy [40].
15.2.2. Miary monotoniczne – zgodne z dominacją stochastyczną.
Miary monotoniczne mają za zadanie oceniać, która inwestycja może przynieść większą stratę. Funkcja
jest monotoniczą miarą ryzyka jeżeli spełnia następujące warunki
Poza tym ,,mile widziane” są następujące własności:
Miary spełniające aksjomaty A1, A2, A3 i A4 nazywa się wypukłymi (patrz [14]).
Natomiast miary spełniające wszystkie pięć aksjomatów to tzw. koherentne miary ryzyka
(patrz [2, 3]). Podstawowym zastosowaniem takich miar jest wyznaczanie wielkości
”kapitału ekonomicznego” potrzebnego do zabezpieczenia danej pozycji.
Przykłady miar monotonicznych.
1. Prawdopodobieństwo nieosiągnięcia wyznaczonego poziomu ![]() (poziomu aspiracji)
(poziomu aspiracji)
Gdy ![]() jest to prawdopodobieństwo poniesienia straty.
jest to prawdopodobieństwo poniesienia straty.
Gdy ![]() , to
, to ![]() spełnia tylko warunki A1 i A2.
spełnia tylko warunki A1 i A2.
2. Value at Risk - największa strata przy zadanym poziomie istotności ![]() (
(![]() ).
).
![]() spełnia warunki A1, A2, A4 i A5, ale na ogół nie spełnia A3 – patrz lemat 15.1.
spełnia warunki A1, A2, A4 i A5, ale na ogół nie spełnia A3 – patrz lemat 15.1.
3. Conditional VaR (zwany też Probable Maximum Loss lub Expected Shortfall) - warunkowa oczekiwana wartość straty pod warunkiem, że osiągnie ona lub przekroczy VaR.
Dla zmiennych losowych ![]() o ciągłym rozkładzie
o ciągłym rozkładzie
![]() jest koherentną miarą ryzyka i spełnia wszystkie pięć aksjomatów (patrz [32, 39, 1]).
jest koherentną miarą ryzyka i spełnia wszystkie pięć aksjomatów (patrz [32, 39, 1]).
4. Spadek oczekiwanej użyteczności.
gdzie ![]() wklęsła i rosnąca funkcja na
wklęsła i rosnąca funkcja na ![]() (funkcja użyteczności) np.
(funkcja użyteczności) np. ![]() .
.![]() spełnia warunki A1, A2 i A3.
spełnia warunki A1, A2 i A3.
5. Miary ryzyka indukowane przez zmianę miary probabilistycznej.
Niech ![]() ,
, ![]() ,
nieujemne zmienne losowe o skończonej wartości oczekiwanej (np. kursy waluty lokalnej w
,
nieujemne zmienne losowe o skończonej wartości oczekiwanej (np. kursy waluty lokalnej w ![]() -tej walucie
lub koszyku walut).
-tej walucie
lub koszyku walut).
Miary indukowane są koherentnymi miarami ryzyka i spełniają wszystkie pięć aksjomatów.
6. Miary wyznaczone przez poziom krytyczny ![]() taki, że wartość oczekiwana jego przekroczenia przez stratę jest
stała i wynosi
taki, że wartość oczekiwana jego przekroczenia przez stratę jest
stała i wynosi ![]() ,
, ![]() .
.
Miary ![]() są wypukłe i spełniają warunki A1, A2, A3 i A4 ([22]).
są wypukłe i spełniają warunki A1, A2, A3 i A4 ([22]).
7. Miary wyznaczone przez poziom krytyczny ![]() taki, że wartość oczekiwana przekroczenia
taki, że wartość oczekiwana przekroczenia ![]() jest
proporcjonalna do
jest
proporcjonalna do ![]() i wynosi
i wynosi ![]() ,
, ![]() .
.
gdzie
Miary ![]() spełniają warunki A1, A2, A3 i A5 ([22]).
spełniają warunki A1, A2, A3 i A5 ([22]).
8. Miary wyznaczone przez poziom krytyczny ![]() taki, że dla ustalonego parametru,
taki, że dla ustalonego parametru, ![]() .
.
Miary ![]() są koherentne i spełniają warunki A1, A2, A3, A4 i A5 ([22]).
są koherentne i spełniają warunki A1, A2, A3, A4 i A5 ([22]).
9. Składka holenderska.
Miary ![]() są koherentne i spełniają warunki A1, A2, A3, A4 i A5.
są koherentne i spełniają warunki A1, A2, A3, A4 i A5.
15.2.3. Miary efektywności
Miary efektywności (performance measures) mają za zadanie ocenić w jakim stopniu dana strategia
inwestycyjna gwarantuje uzyskanie (i przekroczenie) zadanego poziomu aspiracji ![]() .
Zwykle benchmark
.
Zwykle benchmark ![]() jest wielkością deterministyczną, ale może być też zależny od czynników losowych.
jest wielkością deterministyczną, ale może być też zależny od czynników losowych.
Miary efektywności najczęściej konstruowane są jako iloraz dwóch miar:
miary nadwyżki stopy zwrotu nad benchmarkiem ![]()
i miary dyspersji stopy zwrotu względem benchmarku ![]() .
.
Można tu zauważyć pewną analogię z testami statystycznymi dotyczącymi wartości oczekiwanej.
Przykłady miar efektywności ([31]).
Przyjmiemy następujące oznaczenia:![]() – stopa zwrotu z inwestycji, a
– stopa zwrotu z inwestycji, a ![]() – benchmark czyli wymagany poziom stopy zwrotu (poziom aspiracji).
– benchmark czyli wymagany poziom stopy zwrotu (poziom aspiracji).
1. Uogólniony współczynnik Sharpe'a.
2. Współczynnik Sortino.
3. Wskaźnik potencjału nadwyżki (Upside Potential Ratio).
4. Stosunek zysku do straty (Gain-Loss Ratio), zwany też funkcją omega.
Miary 2, 3, i 4, w odróżnieniu od ,,symetrycznego” współczynnika Sharpe'a, określane są w literaturze jako ”Downside Risk Measures”.
15.3. Ćwiczenia
Ćwiczenie 15.1
Wyznacz ![]() dla straty
dla straty ![]() o rozkładzie normalnym,
o rozkładzie normalnym, ![]() , dla
, dla ![]() i dla
i dla ![]() .
.
Rozwiązanie.
gdzie ![]() jest dystrybuantą standardowego rozkładu normalnego.
Zatem
jest dystrybuantą standardowego rozkładu normalnego.
Zatem ![]() a
a ![]() .
.
Odpowiedź.![]() a
a ![]() .
.
Ćwiczenie 15.2
Wyznacz ![]() dla straty
dla straty ![]() o rozkładzie lognormalnym,
o rozkładzie lognormalnym, ![]()
![]() , dla
, dla ![]() .
.
Rozwiązanie.
gdzie ![]() jest dystrybuantą standardowego rozkładu normalnego.
jest dystrybuantą standardowego rozkładu normalnego.
Odpowiedź.![]() ,
gdzie
,
gdzie ![]() jest dystrybuantą standardowego rozkładu normalnego.
jest dystrybuantą standardowego rozkładu normalnego.
Ćwiczenie 15.3
Wyznacz ![]() dla straty
dla straty ![]() o rozkładzie Pareto,
o rozkładzie Pareto, ![]() ,
, ![]() ,
, ![]() dla
dla ![]() i dla
i dla ![]() .
.
Rozwiązanie.
Zatem
Odpowiedź.![]() ,
a
,
a ![]() .
.
Ćwiczenie 15.4
Przybliżamy łączny rozkład dziennych stóp zwrotu kursów USD i EUR w PLN rozkładem normalnym o parametrach:
![]() ,
, ![]() ,
, ![]() i
i ![]() .
Aktualny kurs USD wynosi 3,5 PLN, a EUR – 4 PLN.
Wyznaczyć dzienny Value at Risk dla portfela walutowego złożonego z 20 tys. USD i 10 tys. EUR,
dla
.
Aktualny kurs USD wynosi 3,5 PLN, a EUR – 4 PLN.
Wyznaczyć dzienny Value at Risk dla portfela walutowego złożonego z 20 tys. USD i 10 tys. EUR,
dla ![]() .
.
Rozwiązanie.
Niech ![]() i
i ![]() oznaczają dzienne stopy zwrotu (relatywne przyrosty) kursów USD i EUR.
Oznaczmy przez
oznaczają dzienne stopy zwrotu (relatywne przyrosty) kursów USD i EUR.
Oznaczmy przez ![]() wyrażoną w PLN, możliwą stratę, tzn. różnicę wartości aktualnej portfela i w dniu następnym.
wyrażoną w PLN, możliwą stratę, tzn. różnicę wartości aktualnej portfela i w dniu następnym.
![]() ma rozkład normalny o zerowej wartości oczekiwanej i wariancji
ma rozkład normalny o zerowej wartości oczekiwanej i wariancji
Odchylenie standardowe ![]() wynosi 1300.
Po przybliżeniu kwantyla rozkładu normalnego standardowego przez 1,65
otrzymujemy, że
wynosi 1300.
Po przybliżeniu kwantyla rozkładu normalnego standardowego przez 1,65
otrzymujemy, że ![]() wynosi
wynosi ![]() .
.
Odpowiedź.
Dla poziomu ufności 0,95 Value at Risk wynosi 2145 PLN.




