« 1. Rynek kapitałowy, wiadomości wstępne  Spis treści  3. Struktura terminowa stóp procentowych »  

Zagadnienia

2. Pieniądz

Liczba godzin 2.
Zakres materiału:
Proces bogactwa. Proces akumulacji. Stopa zwrotu. Inflacja i realna stopa zwrotu. Metoda strumieni pieniężnych. Współczynnik dyskonta. Rodzaje kapitalizacji: prosta, składana, ciągła. Struktura liczenia dni (tzw. day count). Inflacja i realna stopa zwrotu

2.1. Opis inwestycji finansowych

2.1.1. Ujęcie ,,globalne”

Rozważmy inwestycję finansową w okresie \langle T_{0},T_{1}\rangle. \; T=T_{1}-T_{0} nazywa się ,,czasem życia inwestycji” lub ,,horyzontem czasowym”.

Inwestycję modelujemy za pomocą procesu bogactwa (wealth process)

K:\langle T_{0},T_{1}\rangle\rightarrow\langle 0,\infty),

gdzie K(t) interpretujemy jako stan posiadania inwestora w chwili t.

W szczególności:
K=K(T_{0}) oznacza kapitał początkowy inwestora,
K(t)=0 dla pewnego t oznacza bankructwo inwestora w chwili t.

Jeżeli dodatkowo założymy, że funkcja K(t) jest rosnąca, to mówimy o procesie akumulacji. Taki proces wykorzystuje się na przykład do modelowania rachunku oszczędnościowego a vista, którego posiadacz nie dokonywał wypłat. Gdy porównujemy wartości procesu akumulacji w dwóch momentach t_{1} i t_{2}, t_{1}<t_{2}, to mówimy, że kwota K(t_{1}) zakumulowała się do kwoty K(t_{2}) lub że wartość skumulowana kwoty K(t_{1}) (zainwestowanej w chwili t_{1}) w chwili t_{2} wyniosła K(t_{2}).

Zysk to różnica wartości procesu bogactwa w dwóch momentach czasu.

Z(t_{2},t_{1})=K(t_{2})-K(t_{1}),\;\;\;\; t_{2}>t_{1}.

Jeśli t_{1} jest momentem rozpoczęcia inwestycji (t_{1}=T_{0}), to zwyczajowo opuszczamy jeden argument funkcji Z.

Z(t)=Z(t,T_{0})=K(t)-K.
Uwaga 2.1

Gdy Z przyjmuje wartość ujemną, wówczas mówimy o stracie.

Jeśli K(t_{1})>0, to możemy określić stopę zwrotu w okresie \langle t_{1},t_{2}\rangle (względny przyrost procesu bogactwa K(t))

r(t_{2},t_{1})=\frac{Z(t_{2},t_{1})}{K(t_{1})}=\frac{K(t_{2})}{K(t_{1})}-1,
r(t)=r(t,T_{0})=\frac{K(t)-K}{K}.

Gdy modelowany proces jest ,,mierzony” w pewnych jednostkach monetarnych, to stopa zwrotu mówi nam, ile wynosi zysk z jednej jednostki monetarnej. Jak łatwo zauważyć, stopy zwrotu wyznaczają proces bogactwa. Mamy

K(t)=(1+r(t))K,\;\;\; K(t_{2})=(1+r(t_{2},t_{1}))K(t_{1}).

Warto zwrócić uwagę na zależność ,,wielookresowej” stopy zwrotu od stóp zwrotu w poszczególnych okresach.

Lemat 2.1

Niech t_{0}<t_{1}<\dots<t_{n}. Jeżeli w okresie \langle t_{{i-1}},t_{i}\rangle stopa zwrotu wynosi r_{i}, i=1,\dots,n, to stopa zwrotu w okresie \langle t_{{0}},t_{n}\rangle wyniesie

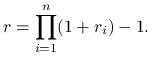r=\prod _{{i=1}}^{n}(1+r_{i})-1.

Dowód.
Korzystamy z zależności

K(t_{i})=K(t_{{i-1}})(1+r(t_{i},t_{{i-1}}))=K(t_{{i-1}})(1+r_{i}),\;\;\; i=1,2,\dots,n.

Mnożąc powyższe równości stronami, a następnie skracając, otrzymujemy

K(t_{n})=K(t_{0})(1+r_{1})\dots(1+r_{n}).

Zatem

r=r(t_{n},t_{0})=\frac{K(t_{n})-K(t_{0})}{K(t_{0})}=(1+r_{1})\dots(1+r_{n})-1.

2.1.2. Ujęcie ,,lokalne”

Z każdą inwestycją związane są przepływy gotówki (cash flows), zwane też przepływami (strumieniami) pieniężnymi

CF_{0},CF_{1},\dots,CF_{n},

które mają miejsce w chwili t_{i}\in\langle T_{0},T_{1}\rangle,

T_{0}=t_{0}<t_{1}<\dots<t_{n}.

Niekiedy będziemy stosowali zapis uproszczony

CF_{{t_{0}}},CF_{{t_{1}}},\dots,CF_{{t_{n}}}.

Ujemna wartość CF_{i} (lub CF_{t}) oznacza wydatki, a dodatnia przychody. Zysk z inwestycji wyznaczamy według następującego wzoru:

Z=CF_{0}+CF_{1}+\dots+CF_{n}.

Gdy rozpatrujemy inwestycję jednookresową (n=1), taką, że CF_{0}<0, a CF_{1}>0 (najpierw inwestujemy), to wzór na stopę zwrotu jest następujacy:

r=\frac{CF_{1}+CF_{0}}{|CF_{0}|}=\frac{CF_{1}}{|CF_{0}|}-1.

Przykład
Inwestor kupił za 100 zł roczną obligację. Po roku wypłata wyniosła 110 zł.
Mamy następujące dane:
czas życia inwestycji 1 rok, zatem t\in\langle 0,1\rangle;
K(0)=100,
K(1)=110.
Dla t\in(0,1) K(t) jest wartością rynkową obligacji w momencie t.
Zysk i stopa zwrotu wynoszą odpowiednio

Z=110-100=10,\;\;\; r=\frac{10}{100}=0,1.

Alternatywny opis wygląda następująco:

CF_{0}=-100,\;\;\; CF_{1}=110.

Zatem zysk i stopa zwrotu wynoszą odpowiednio

Z=-100+110=10,\;\;\; r=\frac{10}{|-100|}=0,1.

Podsumowanie:
Proces bogactwa opisuje stan posiadania inwestora, a przepływy gotówki tylko stan jego rachunku bankowego.

2.2. Przykłady procesów akumulacji

2.2.1. Odsetki proste (procent prosty)

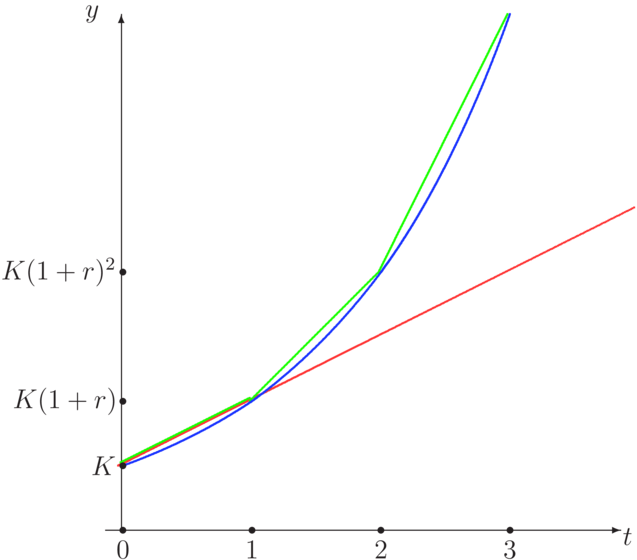
Rachunek oszczędnościowy a vista, z odsetkami naliczanymi proporcjonalnie do czasu utrzymywania lokaty, jest opisywany następującym procesem akumulacji:

K(t)=K\cdot(1+tr),\;\;\mbox{ gdzie $t$ kolejny okres lub jego część, }\;\;\; t\in\langle 0,T\rangle,\;\;\; K=const.

Stopa zwrotu dla takiego procesu wynosi

r(1)=r,\;\;\; r(t)=\frac{K(t)-K}{K}=tr.

2.2.2. Odsetki złożone (procent złożony)

Inna metoda naliczania odsetek opisana jest za pomocą funkcji wykładniczej zależnej od czasu

K(t)=K\cdot(1+r)^{t},\;\;\mbox{ gdzie $t$ kolejny okres, }\;\;\; t\in\langle 0,T\rangle,\;\;\; K=const.

Stopa zwrotu dla takiego procesu wynosi

r(1)=r,\;\;\; r(t)=\frac{K(t)-K}{K}=(1+r)^{t}-1=tr+\frac{t(t-1)}{2}r^{2}+\dots.

Jak widać, różnica między stopami zwrotu powyższych procesów jest rzędu r^{2}.

2.2.3. Okresowa kapitalizacja odsetek

W praktyce stosuje się połączenie obu sposobów oprocentowania. Pomiędzy pełnymi okresami nalicza się odsetki w sposób prosty, a następnie dodaje się odsetki do kapitału (kapitalizacja odsetek).

K(t)=K\cdot(1+r)^{{[t]}}\cdot(1+(t)r),\;\;\;\;\; t\in\langle 0,T\rangle,\;\;\; K=const.

[t] część całkowita, (t) część ułamkowa (czyli t=[t]+(t), gdzie [t]\in\mathbb{Z}, (t)\in\langle 0,1)). Zauważmy, że

r(1)=r,\;\;\; r(t)=\frac{K(t)-K}{K}=(1+r)^{{[t]}}\cdot(1+(t)r)-1.

Poniżej przedstawione są wykresy opisanych powyżej trzech procesów akumulacji:

y=K(1+tr),\;\;\; y=K(1+r)^{t}\;\;\mbox{ oraz }\;\; y=K\cdot(1+r)^{{[t]}}\cdot(1+(t)r).
Rys. 2.1. Porównanie procesów akumulacji..

2.2.4. Kapitalizacja ciągła

Czasami wygodniej jest zapisywać proces akumulacji opisujący procent złożony za pomocą funkcji wykładniczej o podstawie e.

K(t)=K\cdot e^{{t\gamma}},\;\;\;\;\; t\in\langle 0,T\rangle,\;\;\; K=const.

Mówimy wówczas o kapitalizacji ciągłej. Wielkość oznaczoną literą \gamma będziemy nazywać intensywnością oprocentowania. Łatwo wyrazić ją za pomocą stopy procentowej (procent złożony)

\gamma=\ln(1+r),\;\;\; r=e^{{\gamma}}-1.
Uwaga 2.2

W niektórych ,,źródłach” \gamma nazywa się ,,chwilową stopą procentową”.

Aby porównywać różne procesy akumulacji, należy dokonać wyboru wspólnej jednostki czasu i ustalić wzorcowy typ procesu.

2.2.5. Roczna skala czasowa

Od tej chwili jako jednostkę czasu przyjmujemy rok kalendarzowy. Niech \tau – długość okresu mierzona w latach (np. miesiąc, kwartał, …) r – stopa zwrotu jednookresowa (miesięczna, kwartalna, …), a \hat{r}=r\tau^{{-1}} – stopa zwrotu w skali rocznej. Wówczas proces akumulacji opisujący procent prosty przyjmuje następującą postać

K(t)=K\cdot(1+r\frac{t}{\tau})=K\cdot(1+t\hat{r}).

Natomiast dla procentu złożonego mamy

K(t)=K\cdot(1+r)^{{\frac{t}{\tau}}}=K\cdot(1+\tau\hat{r})^{{\frac{t}{\tau}}}.

Jeżeli długość okresu maleje do 0, to otrzymamy w granicy kapitalizację ciągłą z intensywnością równą \hat{r}

\lim _{{\tau\rightarrow 0}}K\cdot(1+\tau\hat{r})^{{\frac{t}{\tau}}}=Ke^{{t\hat{r}}}.

Stąd też nazwa – kapitalizacja ciągła.

Uwaga 2.3

W matematyce aktuarialnej, dla podkreślenia, że stopa procentowa podana jest w skali rocznej, stosuje się symbol i^{{(m)}}. Oznacza on stopę procentową (dla procentu prostego) dla okresu \frac{1}{m} roku w skali rocznej. Jeśli r oznacza oprocentowanie okresowe, to

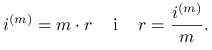i^{{(m)}}=m\cdot r\;\;\;\mbox{ i }\;\;\; r=\frac{i^{{(m)}}}{m}.

Na przykład w ćwiczeniu 2.8 mamy i^{{(4)}}=0,08 i r=0,02.

Uwaga 2.4

W dalszym ciągu będziemy oznaczać stopy zwrotu i stopy procentowe wymiennie literami r i i. Symbol r pochodzi od angielskiego rate of return i chętnie jest używany w finansach, a i od interest rate (lub rate of interest) i używany jest przez aktuariuszy.

2.2.6. Nominalna i efektywna stopa procentowa

Jak już wspominaliśmy, aby móc porównywać różne procesy akumulacji, należy wybrać typ wzorcowy procesu. Wybór oprocentowania prostego prowadzi do stopy nominalnej, a oprocentowania złożonego do stopy efektywnej.

Niech K(t) będzie pewnym procesem akumulacji.

Stopa nominalna w okresie \langle t,t+h\rangle (t czas w latach)

i_{n}=i_{n}(h,t)

to taka stopa procentowa, że

K(t+h)=K(t)\cdot(1+hi_{n}(h,t)),

czyli

i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}.

Stopa efektywna w okresie \langle t,t+h\rangle (t czas w latach)

i_{{ef}}=i_{{ef}}(h,t)

to taka stopa procentowa, że

K(t+h)=K(t)\cdot(1+i_{{ef}}(h,t))^{h},

czyli

i_{{ef}}(h,t)=\sqrt[h]{\frac{K(t+h)}{K(t)}}-1.

Podobnie określa się efektywną intensywność oprocentowania w okresie \langle t,t+h\rangle

\gamma _{{ef}}=\gamma _{{ef}}(h,t).

Jest to taka intensywność, że

K(t+h)=K(t)\cdot e^{{h\gamma _{{ef}}(h,t)}},

czyli

\gamma _{{ef}}(h,t)=\frac{1}{h}\ln(\frac{K(t+h)}{K(t)})=\ln(1+i_{{ef}}(h,t)).

Porównamy teraz graniczne wartości efektywnej intensywności i stopy nominalnej. Okazuje się, że jeżeli istnieją, to są sobie równe.

Lemat 2.2

Dla ustalonego momentu t następujące warunki są równoważne:
1. Prawostronna pochodna K w punkcie t istnieje i jest równa k

k=\lim _{{h\rightarrow 0^{+}}}\frac{K(t+h)-K(t)}{h};

2. Efektywna intensywność \gamma _{{ef}}(h,t) ma w punkcie h=0 granicę \frac{k}{K(t)};
3. Stopa nominalna i_{n}(h,t) ma w punkcie h=0 granicę \frac{k}{K(t)}.

Dowód.
1\Rightarrow 2.
Jeśli K ma w t prawostronną pochodną, to również ma ją złożenie \ln\circ K. Zatem

\gamma _{{ef}}(h,t)=\frac{\ln(K(t+h))-\ln(K(t))}{h}\longrightarrow\ln(K(t))^{\prime}=\frac{k}{K(t)}.

2\Rightarrow 3.
Przedstawimy i_{n} jako iloczyn dwóch funkcji posiadających granicę gdy h\rightarrow 0.

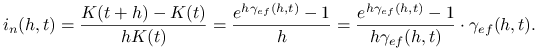i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}=\frac{e^{{h\gamma _{{ef}}(h,t)}}-1}{h}=\frac{e^{{h\gamma _{{ef}}(h,t)}}-1}{h\gamma _{{ef}}(h,t)}\cdot\gamma _{{ef}}(h,t).

Zatem

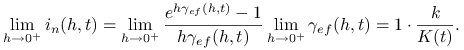\lim _{{h\rightarrow 0^{+}}}i_{n}(h,t)=\lim _{{h\rightarrow 0^{+}}}\frac{e^{{h\gamma _{{ef}}(h,t)}}-1}{h\gamma _{{ef}}(h,t)}\lim _{{h\rightarrow 0^{+}}}\gamma _{{ef}}(h,t)=1\cdot\frac{k}{K(t)}.

3\Rightarrow 1.

\lim _{{h\rightarrow 0^{+}}}\frac{K(t+h)-K(t)}{h}=K(t)\lim _{{h\rightarrow 0^{+}}}\frac{K(t+h)-K(t)}{hK(t)}=
=K(t)\lim _{{h\rightarrow 0^{+}}}i_{n}(h,t)=K(t)\frac{k}{K(t)}=k.

Przykład
Odsetki proste K(t)=(1+tr)K, t\in\langle 0,T\rangle.

i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}=\frac{(1+(t+h)r)K-(1+tr)K}{h(1+tr)K}=
=\frac{hr}{h(1+tr)}=\frac{r}{(1+tr)}.

Jak widać, stopa nominalna nie zależy od długości okresu h i maleje wraz z upływem czasu. Największa wartość przyjmowana jest w momencie początkowym

i_{n}(h,0)=r.
i_{{ef}}(h,t)=\sqrt[h]{\frac{K(t+h)}{K(t)}}-1=\sqrt[h]{\frac{1+(t+h)r}{1+tr}}-1=
=(1+\frac{hr}{1+tr})^{{\frac{1}{h}}}-1

Zauważmy, że dla okresów długości 1 stopa efektywna i nominalna są równe.

i_{{ef}}(1,t)=(1+\frac{r}{1+tr})-1=\frac{r}{1+tr}=i_{n}(1,t).

Efektywna intensywność wynosi

\gamma _{{ef}}(h,t)=\ln(1+i_{{ef}}(h,t))=\frac{1}{h}\ln(1+\frac{hr}{1+tr}).

A więc ona również maleje w miarę upływu czasu.

Przykład
Odsetki złożone K(t)=(1+r)^{t}K, t\in\langle 0,T\rangle.

i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}=\frac{(1+r)^{{h}}-1}{h}.

Zauważmy, że stopa nominalna nie zależy od t. Dla okresów długości 1 wynosi ona

i_{n}(1,t)=r.
i_{{ef}}(h,t)=(\frac{K(t+h)}{K(t)})^{{1/h}}-1=((1+r)^{h})^{{1/h}}-1=r

A zatem stopa efektywna jest stała. Podobnie efektywna intensywność

\gamma _{{ef}}(h,t)=\ln(1+r).

Przykład
Kapitalizacja ciągła K(t)=e^{{rt}}K, t\in\langle 0,T\rangle.

i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}=\frac{1}{h}(e^{{rh}}-1).

Zauważmy, że stopa nominalna nie zależy od t.

i_{{ef}}(h,t)=(\frac{K(t+h)}{K(t)})^{{1/h}}-1=(e^{{rh}})^{{\frac{1}{h}}}-1=e^{r}-1

Jak widać, stopa efektywna jest stała. Podobnie efektywna intensywność

\gamma _{{ef}}(h,t)=\ln(1+i_{{ef}}(h,t))=r.
Uwaga 2.5

W praktyce bankowej dla okresów do jednego roku stosuje się zazwyczaj stopę nominalną, a dla dłuższych efektywną.

2.2.7. Porównanie stopy nominalnej i stopy efektywnej

Niech K(t) będzie dowolnym procesem akumulacji. Okazuje się, że to, która ze stóp, nominalna czy efektywna, jest większa, zależy tylko od długości okresu h.

Lemat 2.3

Dla ustalonego procesu akumulacji K(t) i dowolnego czasu t\geq 0 zachodzą następujące implikacje

\displaystyle 0<h<1 \displaystyle\Rightarrow \displaystyle i_{n}(h,t)<i_{{ef}}(h,t),
\displaystyle h=1 \displaystyle\Rightarrow \displaystyle i_{n}(h,t)=i_{{ef}}(h,t),
\displaystyle h>1 \displaystyle\Rightarrow \displaystyle i_{n}(h,t)>i_{{ef}}(h,t).

Dowód.
Korzystamy ze wzoru na stopę nominalną

i_{n}(h,t)=\frac{K(t+h)-K(t)}{hK(t)}=\frac{1}{h}(\frac{K(t+h)}{K(t)}-1).

Ale jak wcześniej wyliczyliśmy

\frac{K(t+h)}{K(t)}=(i_{{ef}}+1)^{h}=e^{{h\gamma _{{ef}}}}.

Zatem

i_{n}=\frac{1}{h}(e^{{h\gamma _{{ef}}}}-1).

Rozważmy funkcję

f(x)=\frac{e^{x}-1}{x}

dla x>0. Można ją rozwinąć w szereg potęgowy zbieżny na całej prostej rzeczywistej.

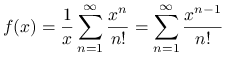f(x)=\frac{1}{x}\sum _{{n=1}}^{{\infty}}\frac{x^{n}}{n!}=\sum _{{n=1}}^{{\infty}}\frac{x^{{n-1}}}{n!}

Pierwszy wyraz rozwinięcia jest stały, a wszystkie pozostałe są ściśle rosnące dla x>0. Zatem f też jest ściśle rosnąca. Zauważmy, że

i_{n}=f(h\gamma _{{ef}})\cdot\gamma _{{ef}}.

Dla h=1 mamy i_{n}=f(\gamma _{{ef}})\cdot\gamma _{{ef}}=e^{{\gamma _{{ef}}}}-1=i_{{ef}}.
Dla 0<h<1 mamy i_{n}<f(\gamma _{{ef}})\cdot\gamma _{{ef}}=e^{{\gamma _{{ef}}}}-1=i_{{ef}}.
Dla h>1 mamy i_{n}>f(\gamma _{{ef}})\cdot\gamma _{{ef}}=e^{{\gamma _{{ef}}}}-1=i_{{ef}}.

Możemy teraz przeformułować uwagę 2.5 z poprzedniego podrozdziału. W praktyce bankowej do określenia wysokości oprocentowania kredytów i lokat używa się \min(i_{n},i_{{ef}}).

2.2.8. Rachunek czasu w matematyce finansowej

Jak ustaliliśmy wcześniej, czas mierzymy w latach. W związku z tym zachodzi pytanie, jak przeliczać dni na lata. Najprościej byłoby podzielić liczbę dni przez długość roku. Problem pojawia się, gdy następuje zmiana roku zwykłego na przestępny lub odwrotnie?

Metody stosowane przez banki.

1. Dokładna liczba dni:

t=\frac{m_{1}}{365}+\frac{m_{2}}{366},

gdzie: m_{1} – liczba dni w roku zwykłym, a m_{2} – w przestępnym. Procent prosty obliczony w oparciu o dokładną liczbę dni nazywa się ,,dokładnym procentem prostym” (exact simple interest).

Metoda ta jest dość skomplikowana rachunkowo, dlatego stosuje się też inne, prostsze.

2. Zasada równych miesięcy.
Przyjmujemy, że każdy miesiąc ma równą liczbę dni – 30, a rok ma ich 360.

t=\frac{m}{360},

gdzie: m – pomnożona przez 30 liczba pełnych kalendarzowych miesięcy, powiększona o liczbę dni z ,,napoczętego” miesiąca.

m=(D_{2}-D_{1})+30\cdot(M_{2}-M_{1})+360\cdot(R_{2}-R_{1}),

D_{1}M_{1}R_{1} oznacza datę rozpoczęcia inwestycji, a D_{2}M_{2}R_{2} datę zakończenia inwestycji. Procent prosty obliczony w oparciu o zasadę równych miesięcy nazywa się ,,zwykłym procentem prostym” (ordinary simple interest).

3. Reguła bankowa (Banker's rule).

t=\frac{m}{360},

gdzie: m – dokładna liczba dni.

2.2.9. Dyskonto

O dyskoncie mówimy, gdy opłata za korzystanie z cudzych pieniędzy jest pobrana z ,,góry”. Stopą dyskonta nazywamy stosunek zysku (zwanego wtedy dyskontem) do końcowej wielkości kapitału.

D(t)=\frac{K(t)-K(0)}{K(t)}.

W skali rocznej stopa ta wynosi

\hat{D}(t)=\frac{K(t)-K(0)}{tK(t)},

gdzie: t – czas w latach. Stopa dyskonta jest ściśle związana ze stopą zwrotu.

Lemat 2.4
(1-D(t))(1+r(t))=1

Dowód.

D(t)=\frac{K(t)-K(0)}{K(t)}=1-\frac{K(0)}{K(t)},
r(t)=\frac{K(t)-K(0)}{K(0)}=\frac{K(t)}{K(0)}-1.

Zatem

(1-D(t))(1+r(t))=(1-(1-\frac{K(0)}{K(t)}))(1+(\frac{K(t)}{K(0)}-1))=\frac{K(0)}{K(t)}\frac{K(t)}{K(0)}=1.

Uwaga. W matematyce aktuarialnej, aby podkreślić, że stopa dyskonta podana jest w skali rocznej, stosuje się symbol d^{{(m)}}. Oznacza on stopę dyskonta dla okresu \frac{1}{m} roku w skali rocznej. Jeśli d=D(\frac{1}{m}) oznacza okresową stopę dyskonta, to

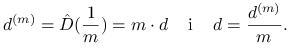d^{{(m)}}=\hat{D}(\frac{1}{m})=m\cdot d\;\;\;\mbox{ i }\;\;\; d=\frac{d^{{(m)}}}{m}.

Okazuje się, że dla krótkiego okresu czasu (czyli dużego m) i ,,gładkiego” procesu akumulacji d^{{(m)}} mało różni się od i^{{(m)}} (wprowadzonego w §1.3.5).

Lemat 2.5

Jeżeli proces akumulacji K(t), t\in\langle 0,T), ma prawostronną pochodną w ,,0” równą k, to

\lim _{{m\rightarrow\infty}}d^{{(m)}}=\lim _{{m\rightarrow\infty}}i^{{(m)}}=\frac{k}{K(0)}.

Dowód.

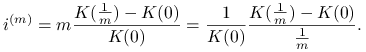i^{{(m)}}=m\frac{K(\frac{1}{m})-K(0)}{K(0)}=\frac{1}{K(0)}\frac{K(\frac{1}{m})-K(0)}{\frac{1}{m}}.

Zatem gdy \frac{1}{m} zbiega do zera, to otrzymujemy w granicy \frac{k}{K(0)}. Podobnie

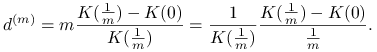d^{{(m)}}=m\frac{K(\frac{1}{m})-K(0)}{K(\frac{1}{m})}=\frac{1}{K(\frac{1}{m})}\frac{K(\frac{1}{m})-K(0)}{\frac{1}{m}}.

Zatem

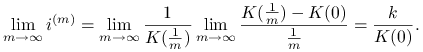\lim _{{m\rightarrow\infty}}i^{{(m)}}=\lim _{{m\rightarrow\infty}}\frac{1}{K(\frac{1}{m})}\lim _{{m\rightarrow\infty}}\frac{K(\frac{1}{m})-K(0)}{\frac{1}{m}}=\frac{k}{K(0)}.

Przykład
Rozważmy proces akumulacji ,,kapitalizacja ciągła” K(t)=K(0)e^{{\gamma t}}. K(t) jest różniczkowalny w ,,0” i K^{\prime}(0)=K(0)\gamma. Zatem

\lim _{{m\rightarrow\infty}}d^{{(m)}}=\lim _{{m\rightarrow\infty}}i^{{(m)}}=\gamma.

2.3. Inflacja i realna stopa zwrotu

Za pomocą procesu bogactwa można też modelować ,,inflację”, czyli spadek wartości wybranej jednostki monetarnej – JM.

Ustalamy pewien koszyk dóbr konsumpcyjnych. Na podstawie cen tych dóbr w chwili t wyznaczamy CPI(t) – indeks cenowy konsumenta (consumer price index), czyli wartość koszyka w chwili t wyrażoną w JM. Stopa inflacji w okresie \langle t_{1},t_{2}\rangle, to względny przyrost CPI

r_{{CPI}}(t_{2},t_{1})=\frac{CPI(t_{2})-CPI(t_{1})}{CPI(t_{1})}.

Niech K(t) będzie pewnym procesem bogactwa. Jeżeli chcemy ocenić, ile dóbr konsumpcyjnych można nabyć za K(t) JM w chwili t, to musimy przeliczyć K(t) na ,,koszyki”, czyli wyznaczyć wielkość zwaną jego realną wartością

K_{{real}}(t)=\frac{K(t)}{CPI(t)}.

Stopę zwrotu procesu bogactwa K_{{real}} nazywamy ,,realną stopą zwrotu”. Można ją łatwo wyznaczyć, znając stopę zwrotu procesu K(t) i stopę inflacji.

Lemat 2.6

Wzór Fishera.

r_{{real}}(t_{2},t_{1})=\frac{r(t_{2},t_{1})-r_{{CPI}}(t_{2},t_{1})}{1+r_{{CPI}}(t_{2},t_{1})}.

Dowód.

r_{{real}}(t_{2},t_{1})=\frac{K_{{real}}(t_{2})}{K_{{real}}(t_{1})}-1=\frac{K(t_{2})}{K(t_{1})}\cdot\frac{CPI(t_{1})}{CPI(t_{2})}-1=
=\frac{1+r(t_{2},t_{1})}{1+r_{{CPI}}(t_{2},t_{1})}-1=\frac{r(t_{2},t_{1})-r_{{CPI}}(t_{2},t_{1})}{1+r_{{CPI}}(t_{2},t_{1})}.

Uwaga. Dla odróżnienia od realnej stopy zwrotu stopę r(t_{2},t_{1}) nazywa się ,,nominalną stopą zwrotu”.

2.4. Ćwiczenia

Ćwiczenie 2.1

Rozważmy proces bogactwa K(t)=t^{2}+2t+3, gdzie t\in\langle 0,1000\rangle – czas w miesiącach,
a) sprawdzić, czy jest to proces akumulacji,
b) obliczyć miesięczny zysk Z_{n} dla n-tego miesiąca,
c) obliczyć miesięczną stopę zwrotu r_{n} dla n-tego miesiąca.

Rozwiązanie.
a) Dla t\geq 0 funkcja kwadratowa K(t)=t^{2}+2t+3 jest ściśle rosnąca, zatem
. K jest procesem akumulacji.
b) Z_{n}=K(n)-K(n-1)=n^{2}+2n+3-(n-1)^{2}-2(n-1)-3=2n+1.
c) r_{n}=\frac{K(n)-K(n-1)}{K(n-1)}=\frac{2n+1}{n^{2}+2}.

Odpowiedź.K jest procesem akumulacji. W n-tym miesiącu zysk wynosi 2n+1, a stopa zwrotu \frac{2n+1}{n^{2}+2}.

Ćwiczenie 2.2

Wiadomo, że proces akumulacji K(t) ma postać a\cdot t^{2}+b, gdzie t\in\langle 0,100\rangle – czas w latach. Wyznaczyć stopę zwrotu w okresie \langle 5,10\rangle, jeżeli wiadomo, że 100 jednostek monetarnych zainwestowanych w chwili 0 akumuluje się do 172 po 3 latach.

Rozwiązanie. Z warunku K(0)=100, wynika, że b=100. Mamy także K(3)=172, co oznacza, że a\cdot 3^{2}+100=172 czyli a=8. Zatem

K(5)=8\cdot 5^{2}+100=300,\;\;\; K(10)=8\cdot 10^{2}+100=900,
r(5,10)=\frac{K(10)-K(5)}{K(5)}=\frac{900-300}{300}=2.

Odpowiedź. Stopa zwrotu w okresie \langle 5,10\rangle wynosi 200%, tzn. w ciągu tych pięciu lat kapitał uległ potrojeniu.

Ćwiczenie 2.3

Inwestor zainwestował na giełdzie 1024 zł. W pierwszym miesiącu poniósł stratę, stopa zwrotu wyniosła –50%. Natomiast w kolejnych miesiącach stopy zwrotu wyniosły +25%.
a) Wyznaczyć stopę zwrotu z pierwszego półrocza.
b) Wyznaczyć wartość inwestycji po pół roku.
c) Po ilu miesiącach inwestycja zaczęła przynosić zysk?

Rozwiązanie. Jako jednostkę czasu przyjmiemy miesiąc.

r(6)=(1-0.5)(1+0.25)^{5}-1=\frac{5^{4}}{2\cdot 4^{5}}-1=\frac{3125}{2048}-1=0.52588.

Zatem

K(6)=K(0)(1+r(6))=1024\frac{3125}{2048}=1562.5.

Ponadto zauważmy, że

r(4)=(1-0.5)(1+0.25)^{3}-1=\frac{125}{128}-1=-0.023<0,
r(5)=(1-0.5)(1+0.25)^{4}-1=\frac{625}{512}-1=0.221>0.

Odpowiedź. Stopa zwrotu za pierwsze półrocze wyniosła 52.59%. Inwestycja po pół roku była warta 1562.5 zł, ale zysk przyniosła dopiero w piątym miesiącu od momemtu zainwestowania pieniędzy.

Ćwiczenie 2.4

Bank udzielił pożyczki w wysokości 1000 zł. Pożyczkobiorca spłacił ją w trzech ratach. Po pół roku wpłacił 500 zł, po 7 miesiącach 300, a po roku kolejne 300. Wyznaczyć łączną kwotę odsetek pobranych przez bank.

Rozwiązanie. Przeanalizujemy zadanie z punktu widzenia banku. Mamy cztery przepływy gotówki

CF_{0}=-1000,\;\;\; CF_{1}=500,\;\;\; CF_{2}=300,\;\;\; CF_{3}=300.

Zatem zysk banku (odsetki) wynosi

Z=CF_{0}+CF_{1}+CF_{2}+CF_{3}=-1000+500+300+300=100.

Odpowiedź. Bank pobrał 100 zł odsetek.

Ćwiczenie 2.5

Obliczyć wartość skumulowaną 2000 EUR zainwestowanych na pół roku na procent prosty, przy stopie procentowej 8% rocznie.

Rozwiązanie. Na podstawie definicji procentu prostego mamy

K(0.5)=2000(1+0.5\cdot 0.08)=2000\cdot 1.04=2080.

Odpowiedź. Po pół roku inwestor otrzymał 2080 EUR.

Ćwiczenie 2.6

Obliczyć wartość skumulowaną 2000 EUR zainwestowanych na cztery lata na procent składany przy stopie procentowej 8% rocznie.

Rozwiązanie. Na podstawie definicji procentu składanego mamy

K(4)=2000(1.08)^{4}=2000\cdot 1.36049=2720.98.

Odpowiedź. Po czterech latach inwestor otrzymał 2720.98 EUR.

Ćwiczenie 2.7

Obliczyć wartość skumulowaną 2000 EUR zainwestowanych na cztery i pół roku przy stopie procentowej 8% rocznie i rocznej kapitalizacji odsetek.

Rozwiązanie. Roczna kapitalizacja odsetek oznacza, że

K(4.5)=2000(1+0.08)(1+0.08)(1+0.08)(1+0.08)(1+0.5\cdot 0.08)=
=2000\cdot 1.08^{4}\cdot 1.04=2000\cdot 1.41491=2829.82.

Odpowiedź. Po czterech i pół roku inwestor otrzymał 2829.82 EUR.

Ćwiczenie 2.8

Obliczyć wartość skumulowaną kwoty 500 zł zainwestowanej na pięć lat na 8% (w skali rocznej) składane kwartalnie.

Rozwiązanie.

K(5)=500\big(1+{0.08\over 4}\big)^{{4\cdot 5}}=500(1.02)^{{20}}=742.97

Odpowiedź. Po pięciu latach inwestor otrzyma 742.97 zł.

Ćwiczenie 2.9

Rozważmy proces akumulacji K(t), gdzie t\in\langle 0,20\rangle czas w latach. Niech r_{n} roczna stopa zwrotu w n-tym roku. Pokazać, że r_{n}=i_{{ef}}(1,n-1).

Rozwiązanie. Z definicji efektywnej 1 rocznej (h=1!) stopy procentowej w n-tym roku mamy

K(n)=K(n-1)(1+i_{{ef}}(1,n-1)).

Zatem

r_{n}=\frac{K(n)}{K(n-1)}-1=\frac{K(n-1)(1+i_{{ef}}(1,n-1))}{K(n-1)}-1=i_{{ef}}(1,n-1).
Ćwiczenie 2.10

Obliczyć wysokość odsetek, jakie zarobił kapitał 2000 USD zdeponowany w banku 17 czerwca 1999 roku, jeśli pieniądze zostały wypłacone 10 września tego samego roku, a stopa procentu prostego wynosiła 8%. Zastosować trzy metody obliczania czasu.

Rozwiązanie. Dokładne oprocentowanie proste. Dokładna liczba dni inwestycji wynosi 85. Zatem otrzymujemy

2000\cdot 0.08{85\over 365}=37.26

Reguła równych miesięcy. Formuła na obliczanie przybliżonej liczby dni daje wynik

360(0)+30(9-6)+(10-17)=83

Stąd

2000\cdot 0.08{83\over 360}=36.89

Natomiast reguła bankiera daje następujący wynik

2000\cdot 0.08{85\over 360}=37.78.

Odpowiedź. Odsetki obliczone według dokładnej liczby dni wyniosły 37.26 USD, zgodnie z zasadą równych miesięcy 36.89 USD, a według reguły bankowej 37.78 USD.

Ćwiczenie 2.11

Porównujemy dwie roczne inwestycje o tej samej stopie zwrotu i tej samej stopie dyskonta. Wiemy o nich, co następuje:
\bullet Inwestycja A. Zysk płatny na końcu roku z zainwestowania kwoty K na jeden rok wynosi 336.
\bullet Inwestycja B. Dyskonto dla wypłaty K wynosi 300.

Obliczyć wielkość kwoty K, roczną stopę zwrotu r i roczną stopę dyskonta d.

Rozwiązanie. Na podstawie warunków zadania mamy

K(1+r)=K+336

oraz

(K-300)(1+r)=K.

Wstawiając 1+r z pierwszego równania do drugiego, dostajemy

(K-300){K+336\over K}=K.

Mnożąc stronami przez K, mamy

(K-300)(K+336)=K^{2}

co sprowadza się do równania

36\cdot K=300\cdot 336

stąd K=2800. Ponadto otrzymujemy

r=\frac{336}{K}=0.12,\;\;\; d=\frac{300}{K}=0.1071.

Odpowiedź. Kwota K wynosi 2800. Natomiast stopy zwrotu i dyskonta wynoszą odpowiednio 12% i 10.71%.

Ćwiczenie 2.12

Bank proponuje swoim klientom roczną lokatę o oprocentowaniu stałym 8%. Wyznaczyć realną stopę zwrotu z tej lokaty, jeśli roczna stopa inflacji \pi wyniesie
a) 5%, b) 7%, c) 10%.

Rozwiązanie.

r_{{real}}=\frac{r-\pi}{1+\pi},

Zatem

r_{a}=\frac{0.08-0.05}{1+0.05}=0.0286,
r_{b}=\frac{0.08-0.07}{1+0.07}=0.0093,
r_{c}=\frac{0.08-0.1}{1+0.1}=-0.0182.

Odpowiedź.Realna stopa zwrotu wyniesie odpowiednio 2.86%, 0.93% i –1.82%.

« 1. Rynek kapitałowy, wiadomości wstępne  Spis treści  3. Struktura terminowa stóp procentowych »  

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

strona główna | webmaster | o portalu | pomoc

© Wydział Matematyki, Informatyki i Mechaniki UW, 2009-2010. Niniejsze materiały są udostępnione bezpłatnie na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Polska.

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Projekt współfinansowany przez Ministerstwo Nauki i Szkolnictwa Wyższego i przez Uniwersytet Warszawski.