5. Wyznaczanie struktury terminowej stóp zwrotu
Liczba godzin 2.
Zakres materiału:
Tworzenie struktury stóp procentowych.
5.1. Wyznaczanie struktury terminowej stóp zwrotu
Empiryczną strukturę terminową wyznaczamy na podstawie następujących danych:
stóp referencyjnych na rynku międzybankowym,
cen,
kuponów i kwot wykupu obligacji
zerokuponowych
i kuponowych o stałym oprocentowaniu
oraz kontraktów FRA.
Przypomnijmy, że przez ![]() oznaczona została funkcja opisująca strukturę terminową czynnika dyskontującego.
oznaczona została funkcja opisująca strukturę terminową czynnika dyskontującego.
5.1.1. Stopy międzybankowe
Niech ![]() oznacza stopę procentową na okres
oznacza stopę procentową na okres ![]() wyrażony w latach. Wówczas przyjmujemy
wyrażony w latach. Wówczas przyjmujemy
5.1.2. Obligacje zerokuponowe i bony
Mamy do czynienia z dwoma przepływami pieniężnymi: zakupem i wykupem obligacji.
Niech ![]() oznacza cenę zakupu,
oznacza cenę zakupu,
![]() – kwotę otrzymaną po wykupieniu obligacji,
a
– kwotę otrzymaną po wykupieniu obligacji,
a ![]() – czas życia obligacji. Wówczas kładziemy
– czas życia obligacji. Wówczas kładziemy
Ta metoda ma istotne ograniczenie. A mianowicie, obligacje zerokuponowe, będące w obrocie rynkowym, mają zwykle krótki termin
do wykupienia. W szczególności czas życia bonów skarbowych nie przekracza jednego roku.
5.1.3. Obligacje kuponowe o stałym oprocentowaniu
Obligacja, z której ![]() krotnie wypłacane są odsetki (
krotnie wypłacane są odsetki (![]() -kuponowa) daje
-kuponowa) daje ![]() przepływów pieniężnych.
Niech
przepływów pieniężnych.
Niech ![]() – cena zakupu obligacji,
– cena zakupu obligacji,
![]() – kupony,
– kupony,
![]() – ostatni kupon i kwota otrzymana po wykupieniu obligacji.
Kolejne przepływy gotówki następują po czasie
– ostatni kupon i kwota otrzymana po wykupieniu obligacji.
Kolejne przepływy gotówki następują po czasie ![]() .
.
Stosuje się dwie metody:
A. Wyznacza się Yield to Maturity (![]() ) – stopę zwrotu liczoną do
momentu zapadalności.
) – stopę zwrotu liczoną do
momentu zapadalności.
B. Oblicza się ![]() w momentach kolejnych przepływów finansowych w sposób łańcuchowy.
w momentach kolejnych przepływów finansowych w sposób łańcuchowy.
5.1.3.1. Yield to Maturity – stopa zwrotu liczona do momentu zapadalności
Założenie toretyczne:
Reinwestujemy otrzymane odsetki ![]() z tą samą efektywną stopą zwrotu.
z tą samą efektywną stopą zwrotu.
Czyli szukamy takiej efektywnej stopy zwrotu ![]() , że
, że
Lub po podzieleniu przez ![]()
Następnie wyznaczamy ![]() z wzoru
z wzoru
Zauważmy, że jest to równoważne przyjęciu, że efektywna stopa zwrotu jest równa stopie zwrotu liczonej do momentu zapadalności
5.1.3.2. Metoda łańcuchowa
Jeśli znamy ![]() dla
dla ![]() , to
, to ![]() wyznaczamy ze wzoru
wyznaczamy ze wzoru
Stosując jedną lub drugą metodę, otrzymujemy wartości ![]() dla skończonej ilości punktów
dla skończonej ilości punktów
![]() . Następnie należy skonstruować funkcję malejącą, która przedłuży naszą empiryczną
. Następnie należy skonstruować funkcję malejącą, która przedłuży naszą empiryczną
![]() określoną dla
określoną dla ![]() , albo dobrać funkcję ,,modelową”, która przybliży empiryczne
, albo dobrać funkcję ,,modelową”, która przybliży empiryczne ![]() .
.
5.1.4. Wyznaczanie struktury terminowej w oparciu o kontrakty FRA
Korzystamy ze wzoru z lematu 3.5.
Jeśli znamy stopę FRA na okres ![]() oraz
oraz ![]() , to wówczas
, to wówczas
5.2. Ćwiczenia
Ćwiczenie 5.1
W dniu 27 sierpnia 2004 roku na Giełdzie Papierów Wartościowych w Warszawie było notowanych pięć serii obligacji zerokuponowych OKmmrr, wszystkie o nominale 1000 zł. Wyznaczyć strukturę terminową.
Rozwiązanie
W poniższej tabeli
podane są ich terminy zapadalności obligacji i ceny, po jakich można było je zakupić. Na tej podstawie
wyznaczone zostały: czas życia ![]() ,
, ![]() ,
, ![]() i
i ![]() .
Dla uproszczenia przyjęliśmy, że 1 dzień, to
.
Dla uproszczenia przyjęliśmy, że 1 dzień, to ![]() część roku.
część roku.
| seria | OK1204 | OK0405 | OK0805 | OK0406 | OK0806 |
| termin | 12.12. | 12.04. | 12.08. | 12.04. | 12.08. |
| zapadalności | 2004 | 2005 | 2005 | 2006 | 2006 |
| cena | |||||
| w zł ( |
980,5 | 957 | 934,8 | 888,5 | 866,4 |
| czas życia | |||||
| w latach ( |
0,2932 | 0,6247 | 0,9589 | 1,6247 | 1,9589 |
| 0,9805 | 0,957 | 0,9348 | 0,8885 | 0,8664 | |
| 0,06718 | 0,07036 | 0,07031 | 0,07277 | 0,07321 | |
| 0,06948 | 0,07290 | 0,07284 | 0,07548 | 0,07595 |
Ćwiczenie 5.2
Rozważmy obligację WS0922. Jest to obligacja o stałym oprocentowaniu 5,75% (w skali roku)
i terminie zapadalności 2022-09-23. Nominał wynosi 1000 zł. Odsetki wypłacane są co roku we wrześniu.
W dniu 11 sierpnia 2004 na GPW w Warszawie za tę obligację płacono 890,90 zł.
Wyznaczyć stopę zwrotu liczoną do momentu zapadalności (![]() ).
).
Rozwiązanie
Stosujemy metodę YTM.
Mamy 19 okresów odsetkowych (![]() ). Z pierwszego pozostało tylko 43 dni, pozostałe są jednoroczne.
). Z pierwszego pozostało tylko 43 dni, pozostałe są jednoroczne.
Czas życia obligacji wynosił
YTM wyznaczamy z równania
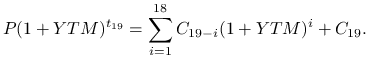 |
Po wstawieniu wartości liczbowych równanie to wygląda następująco:
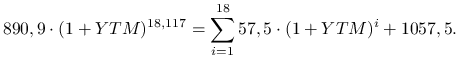 |
Jego jedynym dodatnim pierwiastkiem jest
Zatem
Ćwiczenie 5.3
Rozważmy obligację WS0437. Jest to obligacja o stałym oprocentowaniu 5% (w skali roku)
i terminie zapadalności 2037-04-25. Nominał wynosi 1000 zł. Odsetki wypłacane są co roku w kwietniu.
W dniu 21 listopada 2011 na GPW w Warszawie kurs tej obligacji wynosił 89.
Wyznaczyć stopę zwrotu liczoną do momentu zapadalności (![]() ).
).
Rozwiązanie
Stosujemy metodę YTM.
Mamy 26 okresów odsetkowych (![]() ). Z pierwszego pozostało tylko 156 dni, pozostałe są jednoroczne.
Naliczone odsetki wynoszą (po zaokrągleniu do groszy)
). Z pierwszego pozostało tylko 156 dni, pozostałe są jednoroczne.
Naliczone odsetki wynoszą (po zaokrągleniu do groszy)
Otrzymujemy
Czas życia obligacji wynosił
YTM wyznaczamy z równania
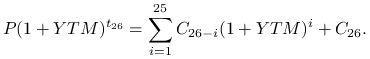 |
Po wstawieniu wartości liczbowych równanie to wygląda następująco:
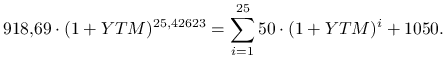 |
Jego jedynym dodatnim pierwiastkiem jest
Ćwiczenie 5.4
Rozważmy grudniowe obligacje z serii SP: SP1206, SP1207 i SP1208. Są to obligacje o stałym oprocentowaniu,
odpowiednio
9,0%, 5,5% i 6,6% (w skali roku),
o terminach zapadalności 2006-12-03, 2007-12-02 i 2008-12-01. Nominał wynosi 100 zł.
Odsetki wypłacane są co roku na początku grudnia.
W dniu 27 sierpnia 2004 na GPW w Warszawie za te obligacje płacono
odpowiednio 109,06 zł, 98,09 zł i 100,35 zł.
Wyznaczyć strukturę terminową.
Rozwiązanie
Stosujemy metodę łańcuchową.
Dla uproszczenia przyjmiemy, że okresy odsetkowe kończą się 2 grudnia.
Wówczas
Wartości ![]() i
i ![]() nie możemy określić za pomocą notowań obligacji serii SP.
Przybliżymy, je korzystając z notowań obligacji zerokuponowych z przykładu 1.8.1.
nie możemy określić za pomocą notowań obligacji serii SP.
Przybliżymy, je korzystając z notowań obligacji zerokuponowych z przykładu 1.8.1.
![]() ,
, ![]() i
i ![]() wyznaczamy metodą łańcuchową.
wyznaczamy metodą łańcuchową.
Zatem ![]() .
.
Czyli ![]() .
.
Otrzymujemy ![]() .
.
Uzyskane wyniki są zebrane w poniższej tabeli.
| seria | SP1206 | SP1207 | SP1208 |
| termin zapadalności | 2006-12-03 | 2007-12-02 | 2008-12-01 |
| kupony | 9,00 | 5,50 | 6,60 |
| cena w zł | 109,06 | 98,09 | 100,35 |
| czas życia w latach ( |
2,27 | 3,27 | 4,26 |
| 0,8441 | 0,7870 | 0,7231 | |
| 0,0776 | 0,0761 | 0,0790 | |
| 0,0747 | 0,0734 | 0,0760 |
Ćwiczenie 5.5
Przedłużamy funkcję ![]() jako funkcję kawałkami wykładniczą (kawałkami płaska struktura terminowa).
Przyjmujemy, że
jako funkcję kawałkami wykładniczą (kawałkami płaska struktura terminowa).
Przyjmujemy, że ![]() i
i ![]() ,
a dla
,
a dla ![]() ,
, ![]() , wyznaczamy
, wyznaczamy ![]() jako ważoną średnią geometryczną
jako ważoną średnią geometryczną ![]() i
i ![]() . Kładziemy
. Kładziemy
Zauważmy, że taka metoda przedłużania ,,zachowuje” płaską strukturę czasową.
Jeśli ![]() dla
dla ![]()
![]() to po przedłużeniu
to po przedłużeniu ![]() dla dowolnego
dla dowolnego ![]() .
.
W oparciu wartości ![]() wyznaczone w ćwiczeniach 5.1 i 5.3
wyznaczyć łączną strukturę terminową.
wyznaczone w ćwiczeniach 5.1 i 5.3
wyznaczyć łączną strukturę terminową.
Rozwiązanie
Mamy
gdzie:
Po przedłużeniu otrzymujemy:
![B(t)=\left\{\begin{array}[]{rcc}\exp(-0,0674t)&\mbox{ dla }&t\in\langle 0,t_{1})\\
1,002\exp(-0,0732t)&\mbox{ dla }&t\in\langle t_{1},t_{2})\\
1,000\exp(-0,0702t)&\mbox{ dla }&t\in\langle t_{2},t_{3})\\
1,006\exp(-0,0763t)&\mbox{ dla }&t\in\langle t_{3},t_{4})\\
1,004\exp(-0,0754t)&\mbox{ dla }&t\in\langle t_{4},t_{5})\\
1,022\exp(-0,0843t)&\mbox{ dla }&t\in\langle t_{5},t_{6})\\
0,990\exp(-0,0703t)&\mbox{ dla }&t\in\langle t_{6},t_{7})\\
1,038\exp(-0,0847t)&\mbox{ dla }&t\in\langle t_{7},t_{8}\rangle\\
\end{array}\right.](wyklady/rka/mi/mi499.png) |




