Zagadnienia
6. Analiza instrumentów dłużnych
Liczba godzin 4.
Zakres materiału:
Wartość obecna, dyskontowanie (tzw. metoda przepływów). Wewnętrzna stopa zwrotu (IRR).
6.1. Wartość obecna – Present Value (PV)
6.1.1. Definicja
Truizmem jest stwierdzenie, że wartość pieniądza zmienia się w czasie.
Wartość obecna (Present Value) przyszłej kwoty ![]() to wartość tej kwoty w chwili obecnej
wyznaczona przez porównanie z lokatą bankową lub inną wzorcową inwestycją.
Zatem jest to kwota pieniędzy, jaką dzisiaj należy:
to wartość tej kwoty w chwili obecnej
wyznaczona przez porównanie z lokatą bankową lub inną wzorcową inwestycją.
Zatem jest to kwota pieniędzy, jaką dzisiaj należy:![]() ulokować w banku na stały procent
ulokować w banku na stały procent
albo![]() zainwestować w bezpieczną inwestycję
zainwestować w bezpieczną inwestycję
tak, aby w przyszłości otrzymać kwotę ![]() .
.
Proces przekształcania przyszłej wartości pieniądza w wartość obecną nazywa się
dyskontowaniem. Pozwala on porównać ze sobą kontrakty finansowe o przepływach gotówki
w różnych momentach czasu. Stosuje się dwie metody dyskontowania:
A. Dyskontujemy za pomocą struktury terminowej stóp procentowych
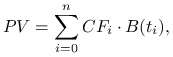 |
gdzie: ![]() – czynnik dyskontujący,
a
– czynnik dyskontujący,
a ![]() – czas, po którym nastąpi
– czas, po którym nastąpi ![]() -ty przepływ gotówki
-ty przepływ gotówki ![]() .
.
B. Dyskontujemy za pomocą wybranego procesu akumulacji ![]() (np. rachunku bankowego a vista),
(np. rachunku bankowego a vista),
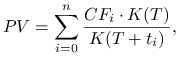 |
gdzie: ![]() – moment dyskontowania (np. moment zawarcia transakcji).
– moment dyskontowania (np. moment zawarcia transakcji).
W zastosowaniach praktycznych częściej stosuje się metodę A, a w rozważaniach teoretycznych – B.
Uwaga.
Czasami wygodniej jest modelować badaną inwestycję za pomocą ciągłego strumienia płatności
z zadaną gęstością ![]() ,
, ![]() . Co oznacza, że wypłatę w okresie od
. Co oznacza, że wypłatę w okresie od ![]() do
do ![]() liczymy wg wzoru
liczymy wg wzoru
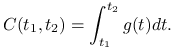 |
Wówczas wartość obecna też wyraża się za pomocą całki
W pewnym sensie oprocentowanie i dyskontowanie są procesami odwrotnymi.
6.1.2. Zależność struktury terminowej od procesu akumulacji
W klasycznych modelach przyjmuje się, że proces akumulacji ![]() jest znany w chwili
jest znany w chwili ![]() i wyznacza strukturę terminową w chwili
i wyznacza strukturę terminową w chwili ![]()
Przy tych założeniach nie ma znaczenia, czy wartość obecną liczymy w oparciu o
strukturę terminową,
czy o proces akumulacji. Obie metody dają ten sam wynik
W nowszym ujęciu modeluje się ![]() jako proces stochastyczny,
na pewnej przestrzeni probabilistycznej
jako proces stochastyczny,
na pewnej przestrzeni probabilistycznej
![]() , która opisuje wszystkie możliwe decyzje ekonomiczne i finansowe
oraz wydarzenia mające wpływ na ekonomię i finanse.
Zdarzeniami elementarnymi (elementami
, która opisuje wszystkie możliwe decyzje ekonomiczne i finansowe
oraz wydarzenia mające wpływ na ekonomię i finanse.
Zdarzeniami elementarnymi (elementami ![]() ) są ciągi decyzji podejmowanych
w kolejnych momentach czasu i wydarzeń mających miejsce w kolejnych momentach czasu.
) są ciągi decyzji podejmowanych
w kolejnych momentach czasu i wydarzeń mających miejsce w kolejnych momentach czasu.
![]() jest rodziną zbiorów decyzji i wydarzeń. Jeżeli
jest rodziną zbiorów decyzji i wydarzeń. Jeżeli ![]() należy do
należy do ![]() , to
, to
![]() jest prawdopodobieństwem, że zostanie podjęta któraś z decyzji
ze zbioru
jest prawdopodobieństwem, że zostanie podjęta któraś z decyzji
ze zbioru ![]() lub nastąpi wydarzenie należące do
lub nastąpi wydarzenie należące do ![]() . Na przykład możemy postawić pytanie, jakie jest prawdopodobieństwo, że
na swoim najbliższym posiedzeniu Rada Polityki Pieniężnej podniesie stopę referencyjną,
albo jakie jest prawdopodobieństwo, że w Japonii w przyszłym roku będzie trzęsienie ziemi.
Następnie przyjmuje się, że
struktura terminowa w chwili
. Na przykład możemy postawić pytanie, jakie jest prawdopodobieństwo, że
na swoim najbliższym posiedzeniu Rada Polityki Pieniężnej podniesie stopę referencyjną,
albo jakie jest prawdopodobieństwo, że w Japonii w przyszłym roku będzie trzęsienie ziemi.
Następnie przyjmuje się, że
struktura terminowa w chwili ![]() wynosi
wynosi
gdzie ![]() jest pewną miarą probabilistyczną na
jest pewną miarą probabilistyczną na ![]() , na ogół tylko równoważną mierze
, na ogół tylko równoważną mierze ![]() ,
,
a ![]() jest
jest ![]() -ciałem zawartym w
-ciałem zawartym w ![]() , które określa zasób informacji dostępny w chwili
, które określa zasób informacji dostępny w chwili ![]() .
Zatem
.
Zatem ![]() to rodzina zbiorów decyzji i wydarzeń znanych w chwili
to rodzina zbiorów decyzji i wydarzeń znanych w chwili ![]() .
Zauważmy, że jeżeli wartość pewnej zmiennej losowej
.
Zauważmy, że jeżeli wartość pewnej zmiennej losowej ![]() będzie znana w chwili
będzie znana w chwili ![]() , to
jest ona
, to
jest ona ![]() -mierzalna.
W szczególności
-mierzalna.
W szczególności ![]() są
są ![]() -mierzalne dla
-mierzalne dla ![]() .
Takie założenia gwarantują, że wartość obecna liczona w oparciu o strukturę terminową
jest równa
wartości oczekiwanej wartości obecnej, liczonej
za pomocą procesu akumulacji.
.
Takie założenia gwarantują, że wartość obecna liczona w oparciu o strukturę terminową
jest równa
wartości oczekiwanej wartości obecnej, liczonej
za pomocą procesu akumulacji.
Niestety ta zgodność nie występuje dla stóp zwrotu.
W modelach deterministycznych
stopa zwrotu wyznaczona przez strukturę terminową ![]() jest równa stopie zwrotu z procesu akumulacji
jest równa stopie zwrotu z procesu akumulacji ![]() .
Natomiast w modelach stochastycznych mogą one być istotnie różne.
.
Natomiast w modelach stochastycznych mogą one być istotnie różne.
Lemat 6.1
Stopa zwrotu wyznaczona przez strukturę terminową jest niewiększa niż wartość oczekiwana
(względem miary ![]() ) stopy zwrotu z procesu akumulacji
) stopy zwrotu z procesu akumulacji
Ponadto równość zachodzi tylko wtedy, gdy warunkowy rozkład ![]() jest jednopunktowy
(tzn. gdy
jest jednopunktowy
(tzn. gdy ![]() jest znane w momencie
jest znane w momencie ![]() ).
).
Dowód – ćwiczenie 6.3
Przykłady:
1. Deterministyczny proces akumulacji typu ,,procent składany”
indukuje płaską strukturę terminową
która ponadto nie zmienia się wraz z upływem czasu (nie zależy od ![]() ).
).
2. Stochastyczny proces akumulacji
gdzie: ![]() stałe,
stałe, ![]() ,
a
,
a ![]() zero-jedynkowa zmienna losowa
zero-jedynkowa zmienna losowa
Wartość ![]() zależy od decyzji, która zostanie podjęta w chwili
zależy od decyzji, która zostanie podjęta w chwili ![]() ,
zatem
,
zatem ![]() jest
jest ![]() -mierzalna dla
-mierzalna dla ![]() .
Ponadto, dla uproszczenia zakładamy, że w mierze
.
Ponadto, dla uproszczenia zakładamy, że w mierze ![]() ,
, ![]() jest niezależna od
jest niezależna od ![]() dla
dla ![]() .
.
Niech ![]() , wówczas
, wówczas
Proszę zwrócić uwagę, że w przypadku ![]() jest to wzór Stoodleya.
jest to wzór Stoodleya.
Dla ![]() otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili
otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili ![]() wartość
wartość ![]() jest już znana (
jest już znana (![]() jest
jest ![]() -mierzalna) zatem
-mierzalna) zatem
Bardziej skomplikowane procesy stochastyczne prowadzą do omówionych wcześniej wzorów Vasička i CIR. W obu modelach
gdzie intensywnośc ![]() , zwana ,,natychmiastową chwilową stopą procentową”, jest procesem
stochastycznym spełniającym stochastyczne równanie różniczkowe.
W modelu Vasička równanie to ma postać
, zwana ,,natychmiastową chwilową stopą procentową”, jest procesem
stochastycznym spełniającym stochastyczne równanie różniczkowe.
W modelu Vasička równanie to ma postać
a w modelu CIR
6.1.3. Dyskontowanie za pomocą płaskiej struktury terminowej
Rozpatrzmy najprostszy przypadek, gdy chwilowa intensywność
jest stała,
![]() .
Wówczas czynnik dyskontujący ma postać
.
Wówczas czynnik dyskontujący ma postać
Ponadto przyjmijmy, że czas życia kontraktu wynosi ![]() lat, a przepływy gotówki mają miejsce raz w roku.
lat, a przepływy gotówki mają miejsce raz w roku.![]() w momencie zawarcia kontraktu,
w momencie zawarcia kontraktu,![]() po 1 roku,
po 1 roku,![]() po 2 latach,
po 2 latach,
…………………………..![]() po
po ![]() latach.
latach.
Dyskontujemy kolejne przepływy
Wartość obecna całego kontraktu jest równa sumie wartości obecnych wszystkich przepływów gotówki
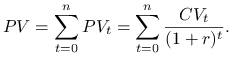 |
Zauważmy, że identyczne wzory otrzymamy, dyskontując za pomocą deterministycznego
procesu akumulacji o stałej (efektywnej) stopie zwrotu.
Uwaga. Przy regularnych przepływach gotówki powyższy wzór można zapisać w postaci łańcuchowej
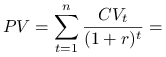 |
6.1.4. Zastosowanie PV
6.1.4.1. Kryterium opłacalności inwestycji.
Rozważmy inwestycję, w czasie trwania której ma miejsce ![]() przepływów gotówki
przepływów gotówki![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() .
Wówczas wartość obecna wynosi
.
Wówczas wartość obecna wynosi
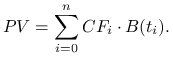 |
Gdy ![]() , to badana inwestycja jest niekorzystna, gdyż
tempo pomnażania kapitału będzie mniejsze niż w przypadku lokat (i kredytów)
ze strukturą terminową opisaną przez
, to badana inwestycja jest niekorzystna, gdyż
tempo pomnażania kapitału będzie mniejsze niż w przypadku lokat (i kredytów)
ze strukturą terminową opisaną przez ![]() i podobnie
będzie mniejsze niż w przypadku zainwestowania posiadanych środków w
deterministyczny proces akumulacji
i podobnie
będzie mniejsze niż w przypadku zainwestowania posiadanych środków w
deterministyczny proces akumulacji ![]() .
.
Gdy ![]() , to badana inwestycja jest korzystna, gdyż
tempo pomnażania kapitału będzie większe niż w przypadku lokat (i kredytów)
ze strukturą terminową opisaną przez
, to badana inwestycja jest korzystna, gdyż
tempo pomnażania kapitału będzie większe niż w przypadku lokat (i kredytów)
ze strukturą terminową opisaną przez ![]() i również
będzie większe niż w przypadku zainwestowania posiadanych środków w
deterministyczny proces akumulacji
i również
będzie większe niż w przypadku zainwestowania posiadanych środków w
deterministyczny proces akumulacji ![]() .
.
6.1.4.2. Kryterium opłacalności zakupu kontraktu.
Rozważmy inwestycję (kontrakt), w czasie trwania której będzie miało miejsce ![]() przepływów gotówki
przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() ,
(np. obligację
,
(np. obligację ![]() -kuponową o stałym oprocentowaniu). Rynkowa cena inwestycji
wynosi
-kuponową o stałym oprocentowaniu). Rynkowa cena inwestycji
wynosi ![]() . Porównując wartość obecną
. Porównując wartość obecną
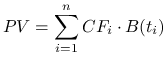 |
z ceną możemy stwierdzić, czy inwestycja jest opłacalna.
Gdy ![]() , to badana inwestycja jest niekorzystna, a gdy
, to badana inwestycja jest niekorzystna, a gdy
![]() , korzystna.
Kryterium to wynika z poprzedniego, gdy przyjmiemy
, korzystna.
Kryterium to wynika z poprzedniego, gdy przyjmiemy ![]() .
.
6.1.4.3. Wycena inwestycji.
Rozważmy inwestycję, w czasie trwania której będzie miało miejsce ![]() przepływów gotówki
przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() ,
(np. obligację
,
(np. obligację ![]() -kuponową o stałym oprocentowaniu). Wartość teoretyczną
takiej inwestycji wyznacza jej wartość obecna.
-kuponową o stałym oprocentowaniu). Wartość teoretyczną
takiej inwestycji wyznacza jej wartość obecna.
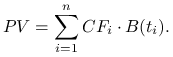 |
Wynika to z faktu, że gdy cena jest równa wartości obecnej, to poprzednie kryterium
nie daje żadnych wskazówek co do kupna lub sprzedaży.
6.1.4.4. Wycena dywidendy płaconej posiadaczowi akcji.
Posiadacz akcji (akcjonariusz) otrzymuje co roku wypłatę części zysku spółki tzw. dywidendę. Wyznaczymy jej wartość obecną przy założeniu, że struktura terminowa jest płaska
![]() Przypadek stałego wzrostu wielkości dywidendy,
Przypadek stałego wzrostu wielkości dywidendy, ![]() ,
, ![]() (model Gordona).
(model Gordona).
Jak widać, gdy stopa wzrostu wielkości dywidendy ![]() dąży do
dąży do ![]() , to wartość dywidendy
rośnie do nieskończoności. Patrz ćwiczenie 6.10.
, to wartość dywidendy
rośnie do nieskończoności. Patrz ćwiczenie 6.10.
![]() Przypadek, gdy dywidenda wzrasta w postępie arytmetycznym,
za rok płacona jest dywidenda
Przypadek, gdy dywidenda wzrasta w postępie arytmetycznym,
za rok płacona jest dywidenda ![]() , a następnie co rok wzrasta o
, a następnie co rok wzrasta o ![]() .
.
Niezależnie od tego, jak duży jest roczny wzrost
wartości dywidendy, jej wartość obecna jest skończona. Patrz ćwiczenie 6.11.
6.2. Ćwiczenia
Ćwiczenie 6.1
Jaka kwota musi być zainwestowana na 9% rocznie przy oprocentowaniu
składanym, by wypłata po trzech latach wyniosła 1000 zł?
Ile wynosi czynnik dyskontujący?
Rozwiązanie.
Oznaczmy przez ![]() szukaną kwotę.
Mamy
szukaną kwotę.
Mamy
Zatem
Odpowiedź.
Należy zainwestować 772,18 zł, a czynnik dyskontujący wynosi 0,77218.
Ćwiczenie 6.2
Jaka kwota musi być zainwestowana na 9% rocznie przy oprocentowaniu
prostym, by wypłata po trzech latach wyniosła 1000 zł?
Ile wynosi czynnik dyskontujący?
Rozwiązanie.
Oznaczmy przez ![]() szukaną kwotę.
Mamy
szukaną kwotę.
Mamy
Zatem
Odpowiedź.
Należy zainwestować 7874,4 zł, a czynnik dyskontujący wynosi 0,78740.
Ćwiczenie 6.3
Udowodnić lemat 6.1.
Rozwiązanie.
Pokażemy, że ![]() .
Wykorzystamy w tym celu nierówność Jensena.
.
Wykorzystamy w tym celu nierówność Jensena.
Zatem
Zauważmy, że funkcja ![]() jest ściśle wypukła, zatem
w przypadku, gdy rozkład nie jest jednopunktowy, to w nierówności Jensena
pojawi się nierówność ostra.
jest ściśle wypukła, zatem
w przypadku, gdy rozkład nie jest jednopunktowy, to w nierówności Jensena
pojawi się nierówność ostra.
Ćwiczenie 6.4
Wyznaczyć strukturę terminową indukowaną przez deterministyczny proces akumulacji
Rozwiązanie.![]() . Zatem
. Zatem
Odpowiedź.
Proces akumulacji typu ,,procent składany” indukuje płaską strukturę terminową
![]() ,
która ponadto nie zmienia się wraz z upływem czasu (nie zależy od
,
która ponadto nie zmienia się wraz z upływem czasu (nie zależy od ![]() ).
).
Ćwiczenie 6.5
Wyznaczyć strukturę terminową indukowaną przez stochastyczny proces akumulacji
gdzie: ![]() stałe,
stałe, ![]() ,
a
,
a ![]() zero-jedynkowa zmienna losowa
zero-jedynkowa zmienna losowa
Wartość ![]() zależy od decyzji, która zostanie podjęta w chwili
zależy od decyzji, która zostanie podjęta w chwili ![]() ,
zatem
,
zatem ![]() jest
jest ![]() -mierzalna dla
-mierzalna dla ![]() .
Ponadto, dla uproszczenia zakładamy, że w mierze
.
Ponadto, dla uproszczenia zakładamy, że w mierze ![]() ,
, ![]() jest niezależna od
jest niezależna od ![]() dla
dla ![]() .
.
Rozwiązanie.
Niech ![]() , wówczas dla
, wówczas dla ![]() otrzymujemy
otrzymujemy
a dla ![]()
Zwróćmy uwagę, że dla ![]() jest to wzór Stoodleya.
jest to wzór Stoodleya.
Dla ![]() otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili
otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili ![]() wartość
wartość ![]() jest już znana (
jest już znana (![]() jest
jest ![]() -mierzalna) zatem
-mierzalna) zatem
Odpowiedź.
Niech ![]() . Wówczas
. Wówczas
Dla ![]() otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili
otrzymujemy wzór analogiczny do wzoru z poprzedniego przykładu. W chwili ![]() wartość
wartość ![]() jest już znana (
jest już znana (![]() jest
jest ![]() -mierzalna) zatem
-mierzalna) zatem
Ćwiczenie 6.6
Wyznaczyć PV dla czteroletnich kredytów opisanych w przykładzie
z punktu 3 podrozdziału 4.1.
Rozpatrzyć trzy przypadki: rynkowa stopa procentowa ![]() równa efektywnej stopie procentowej kredytu,
mniejsza od niej i większa.
równa efektywnej stopie procentowej kredytu,
mniejsza od niej i większa.
Rozwiązanie.
A. ![]() .
.
1. Jednorazowa spłata kapitału i odsetek.
2. Jednorazowa spłata kapitału, odsetki płatne po każdym okresie.
3. Równe raty kapitałowe, odsetki płatne po każdym okresie.
4. Równe spłaty (rata kapitałowa + odsetki = const).
Zgodnie z oczekiwaniami, gdy stopa rynkowa jest równa stopie efektywnej kredytu,
to wartość obecna wszystkich przepływów
jest równa 0. Można to sformułować następująco: wartość obecna spłat jest równa kwocie kredytu.
B. ![]() .
.
1. Jednorazowa spłata kapitału i odsetek.
2. Jednorazowa spłata kapitału, odsetki płatne po każdym okresie.
3. Równe raty kapitałowe, odsetki płatne po każdym okresie.
4. Równe spłaty (rata kapitałowa + odsetki = const).
Zgodnie z oczekiwaniami, gdy stopa rynkowa jest mniejsza od stopy efektywnej kredytu, to wartość obecna wszystkich przepływów
jest dodatnia. Można to sformułować następująco: wartość obecna spłat jest większa niż kwota kredytu.
Różnica między oprocentowaniem kredytu a stopą rynkową nazywa się marżą. Interpretuje się ją jako wynagrodzenie
kredytodawcy za poniesione ryzyko.
C. ![]() .
.
1. Jednorazowa spłata kapitału i odsetek.
2. Jednorazowa spłata kapitału, odsetki płatne po każdym okresie.
3. Równe raty kapitałowe, odsetki płatne po każdym okresie.
4. Równe spłaty (rata kapitałowa + odsetki = const).
Zgodnie z oczekiwaniami, gdy stopa rynkowa jest większa od stopy efektywnej kredytu, to wartość obecna wszystkich przepływów
jest ujemna. Czyli wartość obecna spłat jest mniejsza niż kwota kredytu.
Ćwiczenie 6.7
Pokazać, że
cztery kredyty rozważane w poprzednim ćwiczeniu są opłacalne dla banku wtedy, gdy
stopa efektywna oprocentowania kredytu jest większa niż stopa rynkowa.
Ćwiczenie 6.8
Rozważmy 4 inwestycje o przepływach gotówki, takich jak spłaty kredytów w przykładzie z punktu 3 podrozdziału 4.1.
Przepływy gotówki mają miejsce na koniec roku, czyli ![]() .
.
Wycenić te inwestycje zgodnie z płaską strukturą terminową
dla stopy rynkowej ![]() równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
Odpowiedź.
Otrzymujemy następujące wartości teoretyczne:
![\begin{array}[]{|c|c|c|c|c|}\hline&r=0{,}09&r=0{,}1&r=0{,}11&Stoodley\\
\hline I1&1037{,}2054&1000&964{,}4480&1000{,}8267\\
I2&1032{,}3972&1000&968{,}9755&1000{,}6864\\
I3&1021{,}1189&1000&979{,}6010&1000{,}3600\\
I4&1022{,}0344&1000&978{,}7285&1000{,}3815\\
\hline\end{array}](wyklady/rka/mi/mi689.png) |
Podsumowując, gdy stopa rynkowa jest równa stopie efektywnej oprocentowania, to wartość teoretyczna spłat
kredytu jest równa kwocie kredytu. Natomiast, gdy stopa rynkowa jest mniejsza, to wartość teoretyczna
jest większa. Na odwrót – gdy stopa rynkowa jest większa, to wartość teoretyczna
jest mniejsza. Wycena według wzoru Stoodleya jest nieznacznie większa niż kwota kredytu.
Wynika to z wypukłości funkcji ![]() . Średnia z wycen jest większa niż wycena według
średniej stopy rynkowej.
. Średnia z wycen jest większa niż wycena według
średniej stopy rynkowej.
Ćwiczenie 6.9
W oparciu o płaską strukturę terminową ![]() dokonać wyceny
stałej rocznej dywidendy
dokonać wyceny
stałej rocznej dywidendy ![]() . (Pierwsza wypłata za rok.)
. (Pierwsza wypłata za rok.)
Rozwiązanie.
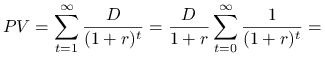 |
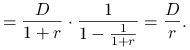 |
Odpowiedź.
Wartość teoretyczna stałej rocznej dywidendy wyznaczona za pomocą płaskiej struktury terminowej wynosi ![]() .
.
Ćwiczenie 6.10
W oparciu o płaską strukturę terminową ![]() dokonać wyceny rocznej dywidendy o stałej stopie wzrostu
dokonać wyceny rocznej dywidendy o stałej stopie wzrostu ![]()
(model Gordona).
Rozwiązanie.
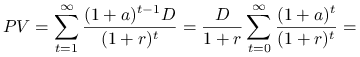 |
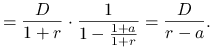 |
Odpowiedź.
Wartość teoretyczna rocznej dywidendy o stałej stopie wzrostu wyznaczona za pomocą płaskiej struktury terminowej wynosi ![]() .
.
Ćwiczenie 6.11
W oparciu o płaską strukturę terminową ![]() dokonać wyceny rocznej dywidendy
wzrastającej w postępie arytmetycznym.
Za rok płacona jest dywidenda
dokonać wyceny rocznej dywidendy
wzrastającej w postępie arytmetycznym.
Za rok płacona jest dywidenda ![]() , a następnie co rok wzrasta o
, a następnie co rok wzrasta o ![]() .
.
Rozwiązanie.
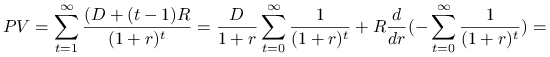 |
Odpowiedź.
Wartość teoretyczna rocznej dywidendy wzrastającej w postępie arytmetycznym wyznaczona za pomocą płaskiej struktury terminowej wynosi ![]() .
.
Ćwiczenie 6.12
Zmarły ojciec zostawił dwóm synom będącym obecnie w wieku 8 i 15 lat lokatę 100 000 USD z zastrzeżeniem,
że każdy odbierze swoją część w rocznicę śmierci ojca po osiągnięciu wieku 21 lat.
Przyjmując stałą efektywną stopę 8% w ciągu 13 przyszłych lat obliczyć, wysokości tych kwot,
jeśli synowie sprawiedliwie podzielą się spadkiem.
Wskazówka: sprawiedliwie oznacza, że wartości obecne obu kwot są równe.
Odpowiedź.
Konkretne kwoty zależą od sposobu w jaki bank zaokrągla odsetki. Jesli przy wypłacie odsetki będą zaokrąglone w dół do 1 USD to młodszy syn otrzyma 135 981 USD, a starszy 79 343 USD.
Ćwiczenie 6.13
Kupiec ma beczkę wina, którą może teraz sprzedać za ![]() złotych
lub też może ją przechować przez okres czasu
złotych
lub też może ją przechować przez okres czasu ![]() (liczony w latach), po czym sprzedać za sumę
(liczony w latach), po czym sprzedać za sumę
![]() . Załóżmy, że struktura terminowa jest płaska,
a intensywność oprocentowania wynosi 0.05 (w skali rocznej).
Wyznaczyć moment najkorzystniejszej dla kupca sprzedaży wina,
tzn.
. Załóżmy, że struktura terminowa jest płaska,
a intensywność oprocentowania wynosi 0.05 (w skali rocznej).
Wyznaczyć moment najkorzystniejszej dla kupca sprzedaży wina,
tzn. ![]() takie, że wartość obecna ceny beczki
przechowanej przez okres czasu
takie, że wartość obecna ceny beczki
przechowanej przez okres czasu ![]() jest największa.
jest największa.
Odpowiedź.
Optymalny moment sprzedaży wynosi 25 lat.




