Zagadnienia
8. Zarządzanie portfelem instrumentów dłużnych
Liczba godzin 2.
Zakres materiału:
Czas trwania (duration) i zmodyfikowany czas trwania. Wypukłość.
Uodpornianie (immunizacja) portfela. Znaczenie duration.
8.1. Duration – średni czas życia i convexity – wypukłość
Rozważmy inwestycję, w czasie trwania której będzie miało miejsce ![]() nieujemnych przepływów gotówki
nieujemnych przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() ,
(np. obligację
,
(np. obligację ![]() -kuponową o stałym oprocentowaniu lub portfel zawierający kilka obligacji).
Załóżmy, że jej wartość obecna jest dodatnia
(tzn. przynajmniej jeden przepływ gotówki jest niezerowy).
-kuponową o stałym oprocentowaniu lub portfel zawierający kilka obligacji).
Załóżmy, że jej wartość obecna jest dodatnia
(tzn. przynajmniej jeden przepływ gotówki jest niezerowy).
Definicja 8.1
Duration, to średni czas życia danej inwestycji ważony udziałem wartości obecnej kolejnych przepływów gotówki w wartości obecnej całej inwestycji
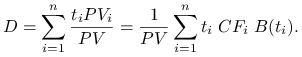 |
Convexity (wypukłość), to średni kwadrat czasu życia danej inwestycji
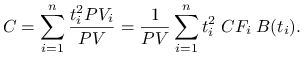 |
Uwaga.
Warto zauważyć, że duration i convexity zdefiniowane zostały za pomocą analogicznych formuł jak
pierwszy i drugi moment zmiennej losowej o rozkładzie dyskretnym. A stąd wynika, że dla
duration i convexity zachodzą podobne zależności jak dla momentów.
Jako przykład wykorzystania tej analogii pokażemy, że średni kwadrat ![]() jest większy od kwadratu średniej
jest większy od kwadratu średniej ![]() .
.
Lemat 8.1
Dla dowolnej inwestycji o dodatnich przepływach gotówki
Ponadto równość zachodzi tylko wtedy, gdy ma miejsce dokładnie jeden niezerowy przepływ gotówki (np. ![]() ).
).
Dowód.
Rozważmy średni kwadrat odchylenia od średniej. Mamy
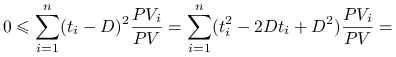 |
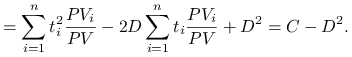 |
8.2. Równoległe przesunięcia struktur terminowych
Z obserwacji rynku wynika, że struktura terminowa stóp procentowych nie jest stała, lecz zmienia się wraz z upływem czasu. Najczęściej obserwowane zmiany polegają na zwiększeniu lub zmiejszeniu średniej efektywnej intensywności o stałą, co wizualnie odpowiada przesunięciu równoległemu jej wykresu. Okazuje się, że wpływ takich zmian na wartość obecną portfela obligacji dobrze charakteryzuje się używając duration i convexity.
Definicja 8.2
Jednoparametrowa rodzina struktur terminowych czynnika dyskontującego
gdzie ![]() ustalona nierosnąca funkcja taka, że
ustalona nierosnąca funkcja taka, że ![]() ,
,
nazywa się równoległym przesunięciem ![]() .
.
Przykład 8.1
Gdy funkcja ![]() jest stała, to znaczy
jest stała, to znaczy
to ![]() ,
, ![]() jest rodziną wszystkich płaskich struktur terminowych.
jest rodziną wszystkich płaskich struktur terminowych.
Przykład 8.2
Gdy funkcja ![]() jest zadane przez intensywność
jest zadane przez intensywność ![]() ,
,
to intensywość ![]() wynosi
wynosi
Ponieważ czynnik dyskontujący jest ściśle malejący, to otrzymujemy następujące oszacowanie ![]()
Jak w podrozdziale 8.1 rozważamy inwestycję, w czasie trwania której będzie miało miejsce ![]() przepływów gotówki
przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() .
Zakładamy, że wszystkie
.
Zakładamy, że wszystkie ![]() są dodatnie.
są dodatnie.
Oznaczmy przez ![]() ,
, ![]() i
i ![]() wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą terminową
wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą terminową ![]() .
.
Lemat 8.2
Dowód.
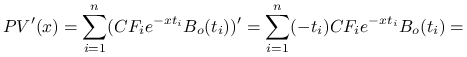 |
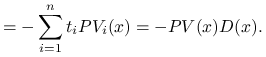 |
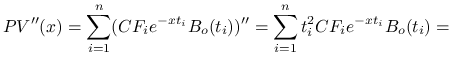 |
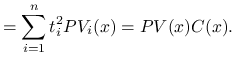 |
Ostatnią równość otrzymamy po zróżniczkowaniu pierwszej.
Po skróceniu przez ![]() otrzymujemy
otrzymujemy
Z lematu 8.1 wynika, że w przypadku, gdy mamy co najmniej dwa dodatnie przepływy gotówki, to pochodna duration jest ujemna. Zatem
Wniosek 8.1
Gdy ![]() to
duration
to
duration ![]() jest ściśle malejącą funkcją zmiennej
jest ściśle malejącą funkcją zmiennej ![]() . Przy przesunięciu równoległym w górę średni czas życia
maleje, a przy przesunięciu w dół rośnie.
. Przy przesunięciu równoległym w górę średni czas życia
maleje, a przy przesunięciu w dół rośnie.
Z punktu widzenia praktyka
duration mierzy liniową część zależności wartości teoretycznej (czyli PV) od
przesunięcia równoległego (czyli od
,,czynnika ryzyka” ![]() ),
a convexity część kwadratową tej zależności. Rzeczywiście po zastosowaniu wzoru Taylora otrzymujemy:
),
a convexity część kwadratową tej zależności. Rzeczywiście po zastosowaniu wzoru Taylora otrzymujemy:
Wniosek 8.2
Dla małych ![]()
Rozważmy teraz ogólniejsze inwestycje, w których mamy do czynienia zarówno
z wypłatami, jak i z wpłatami (przychodami i rozchodami),
tzn. przepływy gotówki mogą być zarówno dodatnie, jak i ujemne.
Niech ![]() oznacza inwestycję, w czasie trwania której będzie miało miejsce
oznacza inwestycję, w czasie trwania której będzie miało miejsce ![]() przepływów gotówki
przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() .
Zakładamy, że przynajmniej jeden przepływ jest dodatni i przynajmniej jeden ujemny.
.
Zakładamy, że przynajmniej jeden przepływ jest dodatni i przynajmniej jeden ujemny.
Przedstawimy ![]() jako różnicę dwóch inwestycji o przepływach nieujemnych
jako różnicę dwóch inwestycji o przepływach nieujemnych
![]() i
i ![]() . W czasie trwania
. W czasie trwania ![]() (
(![]() ) będzie miało miejsce
) będzie miało miejsce ![]() przepływów gotówki
przepływów gotówki
![]() (
(![]() ), odpowiednio w momentach
), odpowiednio w momentach ![]() ,
,
Oznaczmy przez ![]() ,
, ![]() i
i ![]() wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą
wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą ![]() dla inwestycji
dla inwestycji ![]() .
.
Lemat 8.3
Wartość obecna ![]() inwestycji
inwestycji ![]() jest różnicą wartości obecnych
inwestycji
jest różnicą wartości obecnych
inwestycji ![]()
Dowód.
Rzeczywiście dla każdego ![]()
Zatem
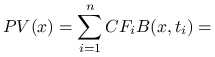 |
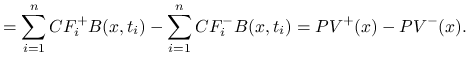 |
Załóżmy dodatkowo, że
dla pewnego ![]() wartości obecne obu inwestycji
wartości obecne obu inwestycji ![]() są równe
są równe ![]() ,
, ![]() ,
,
Wówczas wartość obecna inwestycji ![]()
![]() jest równa 0. Natomiast dla
jest równa 0. Natomiast dla ![]() bliskich
bliskich ![]() wartość obecna
wartość obecna ![]() zależy od duration i convexity
zależy od duration i convexity ![]() .
.
Lemat 8.4
Dla małych ![]()
Zauważmy, że gdy duration są równe, to część liniowa się zeruje i ![]() jest punktem krytycznym
jest punktem krytycznym ![]() .
Jeśli dodatkowo convexity są różne, to w
.
Jeśli dodatkowo convexity są różne, to w ![]() mamy ekstremum lokalne.
mamy ekstremum lokalne.
Wniosek 8.3
Niech ![]() i
i ![]() . Wówczas
. Wówczas
gdy ![]() , to
, to ![]() ma w
ma w ![]() maksimum lokalne,
maksimum lokalne,
a
gdy ![]() , to
, to ![]() ma w
ma w ![]() minimum lokalne.
minimum lokalne.
Jeżeli dodatkowo ograniczymy przemienność wpłat i wypłat, to okaże się, że w punkcie ![]() jest ekstremum globalne. Na przykład, jeśli najpierw mamy serię wypłat, potem serię wpłat i na koniec
znowu serię wypłat, to w
jest ekstremum globalne. Na przykład, jeśli najpierw mamy serię wypłat, potem serię wpłat i na koniec
znowu serię wypłat, to w ![]()
![]() ma globalne minimum.
ma globalne minimum.
Twierdzenie 8.1
Jeżeli ![]() zmieniają dwukrotnie znak
zmieniają dwukrotnie znak
oraz ![]() i
i ![]() , to
, to
![]() ma w punkcie
ma w punkcie ![]() silne minimum globalne
silne minimum globalne
Dowód.
Niech ![]() i
i ![]() rozdzielają momenty przychodów i wydatków
rozdzielają momenty przychodów i wydatków
W dowodzie twierdzenia wykorzystamy następujące oszacowania wariancji ,,czasu życia” inwestycji
![]() .
.
Lemat 8.5
Dla każdego ![]() większego od
większego od ![]()
Dowód lematu.
Zauważmy, że momenty czasu ![]() , w których mają miejsce wydatki spełniają oszacowanie
, w których mają miejsce wydatki spełniają oszacowanie
zatem
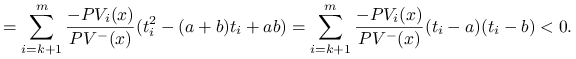 |
Natomiast momenty czasu ![]() , w których mają miejsce przychody, spełniają oszacowanie
, w których mają miejsce przychody, spełniają oszacowanie
zatem
Dowód twierdzenia cd.
Zamiast różnicy ![]() i
i ![]() będziemy badać ich iloraz. Niech
będziemy badać ich iloraz. Niech
Z założenia ![]() wynika, że
wynika, że ![]() .
Pokażemy, że funkcja
.
Pokażemy, że funkcja ![]() ma w tym punkcie silne minimum globalne.
ma w tym punkcie silne minimum globalne.
Z założenia ![]() wynika, że
wynika, że ![]() .
Pokażemy, że jest to jedyny punkt, w którym pochodna
.
Pokażemy, że jest to jedyny punkt, w którym pochodna ![]() się zeruje.
się zeruje.
Niech ![]() . Oczywiście
. Oczywiście ![]() . Z lematu 8.2 otrzymujemy
. Z lematu 8.2 otrzymujemy
Z oszacowania wariancji czasu życia wynika, że gdy dla pewnego ![]()
![]() (czyli
(czyli ![]() ), to
), to ![]() .
Ponieważ
.
Ponieważ ![]() jest funkcją ciągłą, to z powyższego wynika, że
zeruje się ona tylko w punkcie
jest funkcją ciągłą, to z powyższego wynika, że
zeruje się ona tylko w punkcie ![]() i co więcej – zmienia w tym punkcie znak z ,,–” na ,,+”.
Obie wartości obecne są nieujemne, zatem to samo zachodzi dla
i co więcej – zmienia w tym punkcie znak z ,,–” na ,,+”.
Obie wartości obecne są nieujemne, zatem to samo zachodzi dla ![]() ,
,
Czyli ![]() ma w punkcie
ma w punkcie ![]() silne minimum globalne. Zatem
silne minimum globalne. Zatem
Co kończy dowód.
Powyższe fakty są wykorzystywane w praktyce bankowej przy tworzeniu tzw. regulacji ostrożnościowych, które
najczęściej sprowadzają się do ustalenia limitów na moduł różnicy duration dla pasywów
i aktywów (tzw. duration gap)
oraz dla różnicy convexity. Ponadto wymaga się, aby present value pasywów i present value aktywów
były równe.
8.3. Przypadek płaskiej struktury czasowej
Rozważmy płaską strukturę terminową, opisaną
poprzez zależność od stopy procentowej ![]()
Biorąc pod uwagę, że rodzinę płaskich struktur terminowych można przedstawić jako rodzinę przesunięć równoległych
to wyniki z poprzedniego podrozdziału stosują się również do tego przypadku. Co najwyżej należy skorzystać
z twierdzenia o pochodnej funkcji złożonej, aby opisać zależność ![]() od
od ![]() .
.
Jak poprzednio rozważmy inwestycję, w czasie trwania której będzie miało miejsce ![]() dodatnich przepływów gotówki
dodatnich przepływów gotówki
![]() , odpowiednio w momentach
, odpowiednio w momentach ![]() .
Oznaczmy przez
.
Oznaczmy przez ![]() ,
, ![]() i
i ![]() odpowiednio wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą
odpowiednio wartość obecną, duration i convexity wyznaczone zgodnie ze
strukturą ![]() .
.
Lemat 8.6
Dowód - patrz ćwiczenie 8.2.
Uwaga. Iloraz
nazywa się zmodyfikowanym duration
(w odróżnieniu od ![]() zwanego duration Macaulaya).
zwanego duration Macaulaya).
Na podstawie lematu 8.1 wnioskujemy, że gdy co najmniej dwa przepływy gotówki są dodatnie, to pochodna duration jest ujemna. Zatem
Wniosek 8.4
Gdy ![]() to
duration
to
duration ![]() jest ściśle malejącą funkcją
jest ściśle malejącą funkcją ![]() .
Gdy rynkowa stopa procentowa
.
Gdy rynkowa stopa procentowa ![]() rośnie, to
średni czas życia
maleje i na odwrót, gdy
rośnie, to
średni czas życia
maleje i na odwrót, gdy ![]() maleje, to średni czas życia rośnie.
maleje, to średni czas życia rośnie.
Wniosek 8.5
Gdy ![]() to
duration
to
duration ![]() przyjmuje wartości większe niż czas pierwszej wypłaty
przyjmuje wartości większe niż czas pierwszej wypłaty ![]() i mniejsze niż średni czas wypłat ważony udziałem kolejnych wypłat w ich sumie
i mniejsze niż średni czas wypłat ważony udziałem kolejnych wypłat w ich sumie
Dowód - patrz ćwiczenie 8.3.
Z punktu widzenia praktyka
duration mierzy część liniową zależności wartości teoretycznej (czyli PV) od
,,czynnika ryzyka” ![]() ,
a suma duration i convexity część kwadratową tej zależności. Rzeczywiście po zastosowaniu wzoru Taylora otrzymujemy:
,
a suma duration i convexity część kwadratową tej zależności. Rzeczywiście po zastosowaniu wzoru Taylora otrzymujemy:
Wniosek 8.6
Dla małych ![]() prawdziwy jest wzór
prawdziwy jest wzór
8.4. Future Value i immunizacja portfela obligacji
Niech ![]() oznacza wartość obecną inwestycji
oznacza wartość obecną inwestycji ![]() .
.
Future Value ozn. ![]() (wartość przyszła) to wielkość przepływu gotówki po czasie
(wartość przyszła) to wielkość przepływu gotówki po czasie ![]() , którego
wartość obecna jest równa
, którego
wartość obecna jest równa ![]() .
.
W szczególności, jeżeli ![]() generuje tylko jeden przepływ gotówki
generuje tylko jeden przepływ gotówki ![]() , który ma miejsce w momencie
, który ma miejsce w momencie ![]() , to
, to
W modelach opartych na istnieniu deterministycznego procesu akumulacji
![]() , Future Value interpretuje się jako wartość inwestycji
, Future Value interpretuje się jako wartość inwestycji ![]() w chwili
w chwili ![]() .
A dokładniej, jest to suma następujących dwóch kwot: kwoty otrzymanej przez reinwestowanie przepływów gotówki
.
A dokładniej, jest to suma następujących dwóch kwot: kwoty otrzymanej przez reinwestowanie przepływów gotówki
![]() dla
dla ![]() i kwoty równej wartości obecnej pozostałych przepływów gotówki
liczonej po upływie czasu
i kwoty równej wartości obecnej pozostałych przepływów gotówki
liczonej po upływie czasu ![]() . Niech
. Niech ![]() oznacza chwilę obecną, a
oznacza chwilę obecną, a ![]() wartość zreinwestowanej
inwestycji
wartość zreinwestowanej
inwestycji ![]() w momencie
w momencie ![]() . Otrzymujemy:
. Otrzymujemy:
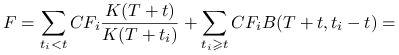 |
Na ogół w modelach stochastycznych powyższy wzór nie zachodzi. Co więcej
może się okazać, że wartość oczekiwana ![]() jest różna od
jest różna od ![]() .
.
Przeanalizujmy jak zmienia się ![]() przy przesunięciu równoległym struktury terminowej.
Niech
przy przesunięciu równoległym struktury terminowej.
Niech ![]() oznacza przepływ gotówki w momencie
oznacza przepływ gotówki w momencie ![]() , a
, a ![]() Future Value inwestycji
Future Value inwestycji ![]() liczoną według
struktury terminowej
liczoną według
struktury terminowej
![]() .
.
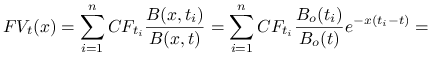 |
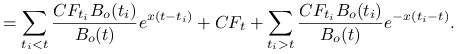 |
Zauważmy, że gdy ![]() rośnie, to rośnie pierwszy składnik i maleje ostatni; na odwrót, gdy
rośnie, to rośnie pierwszy składnik i maleje ostatni; na odwrót, gdy ![]() maleje,
to maleje pierwszy składnik i rośnie ostatni.
maleje,
to maleje pierwszy składnik i rośnie ostatni.
Zachodzi pytanie, w jaki sposób ![]() zależy od
zależy od ![]() . Okazuje się, że w ogólnym przypadku
odpowiedź można sformułować,
wykorzystując duration
. Okazuje się, że w ogólnym przypadku
odpowiedź można sformułować,
wykorzystując duration ![]() . Dla ułatwienia ograniczymy się do takich inwestycji, w których
wszystkie przepływy gotówki są dodatnie i liczba przepływów jest nie mniejsza od dwóch.
. Dla ułatwienia ograniczymy się do takich inwestycji, w których
wszystkie przepływy gotówki są dodatnie i liczba przepływów jest nie mniejsza od dwóch.
Twierdzenie 8.2
Jeżeli wszystkie przepływy gotówki inwestycji ![]() są dodatnie
są dodatnie
oraz ![]() ,
, ![]() , to
, to
![]() ma w punkcie
ma w punkcie ![]() silne minimum globalne
silne minimum globalne
Dowód.
Rozważamy nową inwestycję ![]() złożoną z inwestycji
złożoną z inwestycji ![]() oraz inwestycji
oraz inwestycji ![]() o jednym ujemnym przepływie gotówki
o jednym ujemnym przepływie gotówki
który ma miejsce po upływie czasu ![]() . Zgodnie z twierdzeniem 8.1 Present Value inwestycji
. Zgodnie z twierdzeniem 8.1 Present Value inwestycji ![]()
![]() ma silne globalne minimum w punkcie
ma silne globalne minimum w punkcie ![]()
Ponieważ Future Value jest liniowa ze względu na inwestycje, to
Zatem dla ![]() zachodzi ostra nierówność
zachodzi ostra nierówność
![]() .
.
W przypadku, gdy zachodzi tylko jeden niezerowy przepływ gotówki w chwili ![]() , to
, to
![]() nie zależy od
nie zależy od ![]() , a dla
, a dla ![]() (odpowiednio
(odpowiednio ![]() )
)
![]() jest ściśle malejącą (odp. ściśle rosnącą) funkcją
jest ściśle malejącą (odp. ściśle rosnącą) funkcją ![]() .
.
Uwaga.
Dobór składu portfela obligacji o stałym oprocentowaniu taki, że
średni czas życia portfela pokrywa się z momentem ![]() , dla którego wyznaczamy
Future Value, nazywa się
immunizacją, czyli uodpornieniem portfela.
Według klasycznej teorii, należy tak dobierać skład portfela, aby był on uodporniony na przesunięcie
równoległe struktury terminowej.
, dla którego wyznaczamy
Future Value, nazywa się
immunizacją, czyli uodpornieniem portfela.
Według klasycznej teorii, należy tak dobierać skład portfela, aby był on uodporniony na przesunięcie
równoległe struktury terminowej.
8.5. Ćwiczenia
Ćwiczenie 8.1
Rozważmy, podobnie jak w zadaniu 6.8, 4 inwestycje o przepływach gotówki, takich jak spłaty kredytów w przykładzie z punktu 3 podrozdziału 4.1.
Przepływy gotówki mają miejsce na koniec roku, czyli ![]() .
.
Wyznaczymy duration i convexity tych inwestycji na 4 sposoby. Zgodnie z płaską strukturą terminową
dla stopy rynkowej ![]() równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
Odpowiedź.
Otrzymujemy następujące wartości duration:
![\begin{array}[]{|c|c|c|c|c|}\hline&r=0{,}09&r=0{,}1&r=0{,}11&Stoodley\\
\hline I1&4&4&4&4\\
I2&3{,}4956&3{,}4869&3{,}4781&3{,}4871\\
I3&2{,}2940&2{,}2829&2{,}2719&2{,}2832\\
I4&2{,}3925&2{,}3812&2{,}3700&2{,}3815\\
\hline\end{array}](wyklady/rka/mi/mi994.png) |
i convexity:
![\begin{array}[]{|c|c|c|c|c|}\hline&r=0{,}09&r=0{,}1&r=0{,}11&Stoodley\\
\hline I1&16&16&16&16\\
I2&13{,}1651&13{,}1187&13{,}0720&13{,}1201\\
I3&6{,}4804&6{,}4264&6{,}3731&6{,}4278\\
I4&6{,}9662&6{,}9104&6{,}8552&6{,}9119\\
\hline\end{array}](wyklady/rka/mi/mi1003.png) |
Ćwiczenie 8.2
Udowodnij lemat 8.6
Rozwiązanie.
Niech ![]() . Wówczas
. Wówczas
Ćwiczenie 8.3
Udowodnij wniosek 8.5
Rozwiązanie.
Zauważmy, że granice ![]() wynoszą odpowiednio:
wynoszą odpowiednio:
Ćwiczenie 8.4
Zakładając, że wypłaty następują na koniec roku oraz
że struktura terminowa jest płaska i stopa procentowa ![]() wynosi (w skali rocznej) 10%,
obliczyć średni czas życia (duration) i wypukłość (convexity) następujących obligacji
w dniu emisji (pięć lat przed wykupem):
wynosi (w skali rocznej) 10%,
obliczyć średni czas życia (duration) i wypukłość (convexity) następujących obligacji
w dniu emisji (pięć lat przed wykupem):
1. pięcioletnia obligacja z kuponem zerowym.
2. pięcioletnia obligacja z kuponem 10%.
3. pięcioletnia obligacja z kuponem 8%.
Rozwiązanie.
Oznaczmy przez ![]() wartość nominalną obligacji.
wartość nominalną obligacji.
1. Ponieważ jest tylko jedna płatność w przyszłości
Zatem
2. Mamy pięć płatności.
Wzór na wartość obecną przybierze postać
Zatem
3. Jak poprzednio, mamy pięć płatności.
Wzór na wartość obecną przybierze postać
Zatem
Odpowiedź.
Średni czas życia i wypukłość wynoszą odpowiednio:
– dla obligacji zerokuponowej: 5 i 25,
– dla obligacji z kuponem 10%: 4,1699 i 19,2658,
– a dla obligacji z kuponem 8%: 4,2814 i 20,0363.
Ćwiczenie 8.5
Zakładając, że wypłaty następują na koniec roku oraz
że struktura terminowa jest płaska i stopa procentowa ![]() wynosi (w skali rocznej) 10%,
obliczyć średni czas życia (duration) i wypukłość (convexity) następujących inwestycji:
wynosi (w skali rocznej) 10%,
obliczyć średni czas życia (duration) i wypukłość (convexity) następujących inwestycji:
1. pięcioletnia spłata kredytu, raty w równej wysokości zawierają spłatę
kapitału i odsetki.
2. renta płacąca odsetki w nieskończoność.
Rozwiązanie.
Oznaczmy przez ![]() kwotę pojedynczej płatności.
kwotę pojedynczej płatności.
1.
Mamy pięć płatności
Wzór na wartość obecną przybierze postać
Zatem
2. Mamy nieskończenie wiele płatności
Wzór na wartość obecną przybierze postać
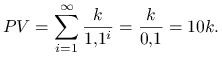 |
Zatem
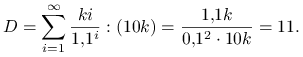 |
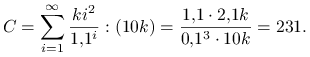 |
Skorzystaliśmy tutaj z następujących wzorów sumacyjnych dla ![]()
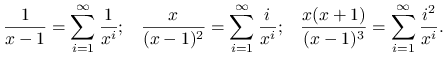 |
Odpowiedź.
Średni czas życia i wypukłość wynoszą odpowiednio:
– dla renty pięcioletniej: 2,8101 i 9,8734,
– a dla renty ,,nieskończonej”: 11 i 231.
Ćwiczenie 8.6
Rozważmy 4 inwestycje o następujących przepływach gotówki:
Przepływy gotówki mają miejsce na koniec roku, czyli ![]() .
.
Wyznaczyć Future Value tych inwestycji na 4 sposoby. Zgodnie z płaską strukturą terminową
dla stopy rynkowej ![]() równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
równej
odpowiednio 9%, 10% i 11% oraz zgodnie ze wzorem Stoodleya
Odpowiedź.
Otrzymujemy następujące wartości ![]() :
:
![\begin{array}[]{|c|c|c|c|c|}\hline&r=0{,}09&r=0{,}1&r=0{,}11&Stoodley\\
\hline I1&1232{,}304&1210&1188{,}296&1210{,}700\\
I2&1226{,}591&1210&1193{,}875&1210{,}530\\
I3&1213{,}191&1210&1206{,}966&1210{,}135\\
I4&1214{,}279&1210&1205{,}891&1210{,}162\\
\hline\end{array}](wyklady/rka/mi/mi878.png) |
i ![]() :
:
![\begin{array}[]{|c|c|c|c|c|}\hline&r=0{,}09&r=0{,}1&r=0{,}11&Stoodley\\
\hline I1&1464{,}100&1464{,}1&1464{,}100&1464{,}100\\
I2&1457{,}313&1464{,}1&1470{,}973&1463{,}895\\
I3&1441{,}393&1464{,}1&1487{,}103&1463{,}417\\
I4&1442{,}685&1464{,}1&1485{,}779&1463{,}449\\
\hline\end{array}](wyklady/rka/mi/mi877.png) |
Podsumowując, gdy stopa rynkowa jest równa efektywnej stopie oprocentowania kredytu, to
future value nie zależy od sposobu spłaty kredytu.
Ćwiczenie 8.7
Inwestor ma do dyspozycji: obligacje 4 letnie, o wartości nominalnej 100 zł
i oprocentowane w wysokości 5% rocznie – płatne co rok, oraz roczne bony skarbowe
o wartości nominalnej 100 zł. Zakładamy, że struktura terminowa stóp procentowych jest płaska,
aktualna stopa procentowa wynosi 5%, a pierwsze wypłaty nastąpią za rok.
a. Wyznaczyć Present Value, Duration i Covexity dla obligacji oraz dla bonów.
b. Jaki
powinien być skład portfela inwestora, aby Future Value dla ![]() lata
wynosiła 1 390 252,5 zł i była uodporniona na wahania stopy procentowej?
lata
wynosiła 1 390 252,5 zł i była uodporniona na wahania stopy procentowej?
Rozwiązanie.
a. Ponieważ stopa rynkowa jest równa stopie oprocentowania obligacji to Present Value jest równe wartości nominalnej
Natomiast Duration i Convexity wynoszą odpowiednio
Ponieważ bony generują tylko jeden przyszły przepływ gotówki (po 1 roku) to
b.
Zgodnie z twierdzeniem 8.2 portfel będzie uodporniony gdy jego Duration wyniesie 3 lata (![]() ).
Zatem aby wyznaczyć liczbę obligacji (
).
Zatem aby wyznaczyć liczbę obligacji (![]() ) i bonów (
) i bonów (![]() ) musimy rozwiązać układ równań:
) musimy rozwiązać układ równań:
Z drugiego równania otrzymujemy
Czyli
Po wstawieniu do pierwszego równania otrzymujemy
Co po uproszczeniu daje
czyli
Odpowiedź.
a. Dla obligacji Present Value, Duration i Covexity wynoszą odpowiednio
100, 3,723 i 14,439,
a dla bonów
95,238, 1 i 1.
b. Porfel spełniający warunki zadania skład się z 8 820 czteroletnich obligacji i 3 349 rocznych bonów.




