Zagadnienia

1.1 Zadania

1. Zbieżność według rozkładu – zbieżność miar probabilistycznych w przestrzeniach metrycznych

Celem tego rozdziału jest wprowadzenie pewnego nowego typu zbieżności zmiennych losowych, tzw. zbieżności według rozkładu. Zacznijmy od pewnych intuicji związanych z tym pojęciem. Jak sama nazwa wskazuje, zbieżność ta odnosi się do rozkładów zmiennych losowych. Zatem, aby ją zdefiniować (na początek, dla rzeczywistych zmiennych losowych), potrzebujemy metody pozwalającej stwierdzić czy dwa rozkłady prawdopodobieństwa na $\mathbb{R}$ są ,,bliskie”. Jeśli tak na to spojrzeć, to automatycznie narzuca się użycie tzw. całkowitej wariacji miary. Ściślej, definiujemy odległość dwóch miar probabilistycznych $\mu$ , $\nu$ na $\mathbb{R}$ jako całkowitą wariację ich różnicy:

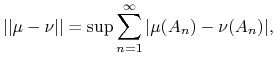$||\mu-\nu||=\sup\sum _{{n=1}}^{\infty}|\mu(A_{n})-\nu(A_{n})|,$

gdzie supremum jest wzięte po wszystkich rozbiciach prostej rzeczywistej na przeliczalną liczbę zbiorów borelowskich $(A_{n})_{{n=1}}^{\infty}$ . I teraz mówimy, że $X_{n}$ zbiega do $X$ jeśli $||P_{{X_{n}}}-P_{X}||\to 0$ gdy $n\to\infty$ .

To podejście jest jednak zbyt restrykcyjne i zbieżność według rozkładu wprowadzimy w inny sposób. W całym niniejszym rozdziale, $(E,\rho)$ jest przestrzenią metryczną, $\mathcal{B}(E)$ oznacza klasę podzbiorów borelowskich $E$ oraz

$C(E)=\{ f:E\to\mathbb{R}\,\,\text{ciągłe i ograniczone}\}.$

Definicja 1.1

Niech $(P_{n})_{n}$ będzie ciągiem miar probabilistycznych na $\mathcal{B}(E)$ (rozkładów prawdopodobieństwa na $E$ ). Mówimy, że ciąg $(P_{n})$ jest zbieżny według rozkładu do $P$ (lub słabo zbieżny do $P$ ), jeżeli dla każdej funkcji $f\in C(E)$ mamy $\int _{E}fdP_{n}\to\int _{E}fdP$ . Oznaczenie: $P_{n}\Rightarrow P$ .

Dowód poprawności definicji: Musimy udowodnić, że jeśli $P_{n}\Rightarrow P$ oraz $P_{n}\Rightarrow P^{{\prime}}$ , to $P=P^{{\prime}}$ . Innymi słowy, musimy wykazać następujący fakt.

Stwierdzenie 1.1

Załóżmy, że $P$ , $P^{{\prime}}$ są takimi rozkładami w $E$ , że dla każdej funkcji $f\in C(E)$ , $\int _{E}fdP=\int _{E}fdP^{{\prime}}$ . Wówczas $P=P^{{\prime}}$ .

Przytoczmy pomocniczy fakt z Topologii I.

Lemat 1.1

Niech $F$ będzie domkniętym podzbiorem $E$ . Wówczas dla każdego $\varepsilon>0$ istnieje $f\in C(E)$ jednostajnie ciągła spełniająca $0\leq f\leq 1$ oraz

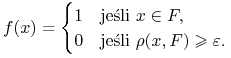$f(x)=\begin{cases}1&\text{jeśli }x\in F,\\ 0&\text{jeśli }\rho(x,F)\geq\varepsilon.\end{cases}$

Dowód Stwierdzenia 1.1:

Wystarczy udowodnić, że dla każdego domkniętego $F\subset E$ zachodzi $P(F)=P^{{\prime}}(F)$ (teza wynika wówczas prosto z lematu o $\pi-\lambda$ układach). Dla każdego $n$ i $\varepsilon=1/n$ , Lemat 1.1 daje funkcję $f_{n}$ o odpowiednich własnościach. Widzimy, iż dla każdego $x\in E$ , $f_{n}(x)\to 1_{F}(x)$ , zatem

$P(F)=\int _{E}1_{F}dP\leftarrow\int _{E}f_{n}dP=\int _{E}f_{n}dP^{{\prime}}\to P^{{\prime}}(F).$

∎

Przykłady:

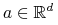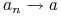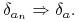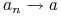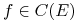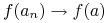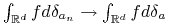Załóżmy, że $(a_{n})$ jest ciągiem punktów z $\mathbb{R}^{d}$ oraz $a\in\mathbb{R}^{d}$ . Wówczas $a_{n}\to a$ wtedy i tylko wtedy, gdy $\delta _{{a_{n}}}\Rightarrow\delta _{a}.$ Istotnie, $a_{n}\to a$ wtedy i tylko wtedy, gdy dla każdej funkcji $f\in C(E)$ mamy $f(a_{n})\to f(a)$ , czyli $\int _{{\mathbb{R}^{d}}}fd\delta _{{a_{n}}}\to\int _{{\mathbb{R}^{d}}}fd\delta _{a}$ .
Załóżmy, że 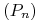$(P_{n})$ jest ciągiem miar probabilistycznych na 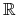$\mathbb{R}$ , zadanym przez

$P_{n}(\{ k/n\})=1/n,\qquad k=1,\, 2,\,\ldots,\, n.$

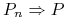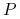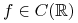Wówczas $P_{n}\Rightarrow P$ , gdzie $P$ jest rozkładem jednostajnym na $[0,1]$ . Istotnie, dla dowolnej funkcji $f\in C(\mathbb{R})$ ,

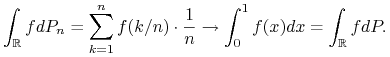
$\int _{\mathbb{R}}fdP_{n}=\sum _{{k=1}}^{n}f(k/n)\cdot\frac{1}{n}\to\int _{0}^{1}f(x)dx=\int _{\mathbb{R}}fdP.$

Ważna uwaga: Z tego, że $P_{n}\Rightarrow P$ nie wynika, że dla dowolnego $B\in\mathcal{B}(E)$ mamy $P_{n}(B)\to P(B)$ . Np. weźmy $a\in\mathbb{R}$ oraz ciąg $(a_{n})$ liczb rzeczywistych taki, że $a_{n}>a$ oraz $a_{n}\to a$ . Jak już wiemy, $\delta _{{a_{n}}}\to\delta _{a}$ , ale

$\delta _{{a_{n}}}((-\infty,a])=0\not\to 1=\delta _{a}((-\infty,a]).$

Twierdzenie 1.1

Niech $P_{n}$ , $P$ ( $n=1,\, 2,\,\ldots)$ będą miarami probabilistycznymi na $\mathcal{B}(E)$ . Następujące warunki są równoważne.

a) $P_{n}\Rightarrow P$ .

b) Dla każdej funkcji $f\in C(E)$ jednostajnie ciągłej, $\int _{E}fdP_{n}\to\int _{E}fdP$ .

c) Dla każdego domkniętego $F\subset E$ , $\limsup _{{n\to\infty}}P_{n}(F)\leq P(F)$ .

d) Dla każdego otwartego $G\subset E$ , $\liminf _{{n\to\infty}}P_{n}(G)\geq P(G)$ .

e) Dla każdego $A\in\mathcal{B}(E)$ takiego, że $P(\partial A)=0$ , mamy $\lim _{{n\to\infty}}P_{n}(A)=P(A)$ .

Dowód:

a) $\Rightarrow$ b) – oczywiste.

b) $\Rightarrow$ c) Ustalmy $\varepsilon>0$ i niech $F_{\varepsilon}=\{ x\in E:\rho(x,F)\leq\varepsilon\}$ . Na mocy Lematu 1.1 istnieje $f_{\varepsilon}\in C(E)$ jednostajnie ciągła, przyjmująca wartości w $[0,1]$ , równa $1$ na $F$ oraz $0$ na $F_{\varepsilon}^{c}$ . Mamy

$P_{n}(F)=\int _{F}f_{\varepsilon}dP_{n}\leq\int _{E}f_{\varepsilon}dP_{n}\to\int _{E}f_{\varepsilon}dP=\int _{{F_{\varepsilon}}}f_{\varepsilon}dP\leq P(F_{\varepsilon}).$

Zatem $\limsup _{n}P_{n}(F)\leq P(F_{\varepsilon})$ , i z dowolności $\varepsilon$ wynika, co trzeba.

c) $\Rightarrow$ a) Wystarczy udowodnić, że dla każdej funkcji $f\in C(E)$ ,

$\limsup _{n}\int _{E}fdP_{n}\leq\int _{E}fdP,$

(1.1)

gdyż po zastąpieniu $f$ przez $-f$ dostaniemy $\liminf _{n}\int _{E}fdP_{n}\geq\int _{E}fdP$ , a więc w rzeczywistości mamy równość, gdyż $\liminf\leq\limsup$ .

Zauważmy, że jeśli $f\in C(E)$ , to istnieją $a>0$ oraz $b\in\mathbb{R}$ takie, że $af+b$ przyjmuje wartości w przedziale $(0,1)$ . Co więcej, jeśli wykażemy (1.1) dla $af+b$ , to nierówność będzie także zachodzić dla $f$ . Innymi słowy, możemy bez straty ogólności założyć, że $0<f(x)<1$ dla każdego $x\in E$ .

Ustalmy taką funkcję $f$ i weźmy dodatnią liczbę całkowitą $k$ . Rozważmy zbiory

$A_{i}=\left\{ x\in E:\frac{i-1}{k}\leq f(x)<\frac{i}{k}\right\},\qquad i=1,\, 2,\,\ldots,\, k.$

Oczywiście $\bigcup _{{i=1}}^{k}A_{i}=E$ oraz zbiory $A_{1},\, A_{2},\,\ldots,\, A_{k}$ są parami rozłączne. Ponadto,

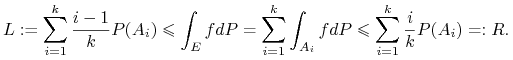$L:=\sum _{{i=1}}^{k}\frac{i-1}{k}P(A_{i})\leq\int _{E}fdP=\sum _{{i=1}}^{k}\int _{{A_{i}}}fdP\leq\sum _{{i=1}}^{k}\frac{i}{k}P(A_{i})=:R.$

Zauważmy, że

$A_{i}=\left\{ x:\frac{i-1}{k}\leq f(x)\right\}\setminus\left\{ x:\frac{i}{k}\leq f(x)\right\}=:F_{{i-1}}\setminus F_{i},$

i $\emptyset=F_{k}\subset F_{{k-1}}\subset\ldots F_{1}\subset F_{0}=E$ jest zstępującym ciągiem zbiorów domkniętych. Zatem $P(A_{i})=P(F_{{i-1}})-P(F_{i})$ , $i=1,\, 2,\,\ldots,\, k$ , i podstawiając dostajemy

$\begin{split} L&=\sum _{{i=1}}^{k}\frac{i-1}{k}(P(F_{{i-1}})-P(F_{i}))=\sum _{{i=0}}^{{k-1}}\frac{i}{k}P(F_{{i}})-\sum _{{i=1}}^{k}\frac{i-1}{k}P(F_{i})\\ &=-\frac{k-1}{k}P(F_{k})+\frac{1}{k}\sum _{{i=1}}^{{k-1}}P(F_{i})=\frac{1}{k}\sum _{{i=1}}^{{k-1}}P(F_{i})\end{split}$

oraz

$\begin{split} R&=\sum _{{i=1}}^{k}\frac{i}{k}(P(F_{{i-1}})-P(F_{i}))=\sum _{{i=0}}^{{k-1}}\frac{i+1}{k}P(F_{{i}})-\sum _{{i=1}}^{k}\frac{i}{k}P(F_{i})\\ &=-P(F_{k})+\frac{1}{k}\sum _{{i=0}}^{{k-1}}P(F_{i})=\frac{1}{k}+\frac{1}{k}\sum _{{i=1}}^{{k-1}}P(F_{i}).\end{split}$

Przeprowadzamy analogiczne oszacowania dla $\int _{E}fdP_{n}$ : w szczególności mamy

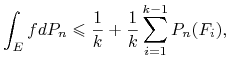$\int _{E}fdP_{n}\leq\frac{1}{k}+\frac{1}{k}\sum _{{i=1}}^{{k-1}}P_{n}(F_{i}),$

skąd wynika, na mocy c),

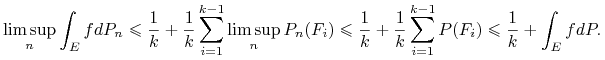$\limsup _{n}\int _{E}fdP_{n}\leq\frac{1}{k}+\frac{1}{k}\sum _{{i=1}}^{{k-1}}\limsup _{n}P_{n}(F_{i})\leq\frac{1}{k}+\frac{1}{k}\sum _{{i=1}}^{{k-1}}P(F_{i})\leq\frac{1}{k}+\int _{E}fdP.$

Wystarczy tylko zbiec z $k$ do nieskończoności.

c) $\Leftrightarrow$ d): oczywiste po przejściu do dopełnień zbiorów.

c) $\Rightarrow$ e) Załóżmy, że $A\in\mathcal{B}(E)$ spełnia warunek $P(\partial A)=0$ . Ponieważ $\partial A=\overline{A}\setminus\text{int}A$ oraz $\text{int}A\subseteq\overline{A}$ , mamy $P(\overline{A})=P(\text{int}A)=P(A)$ . Z drugiej strony, korzystając z c) oraz d), mamy

$\begin{split} P(\overline{A})&\geq\limsup _{n}P_{n}(\overline{A})\geq\limsup _{n}P_{n}(A)\\ &\geq\liminf _{n}P_{n}(A)\geq\liminf _{n}P_{n}(\text{int}A)\geq P(\text{int}A),\end{split}$

a zatem wszędzie mamy równości: to oznacza tezę podpunktu e).

e) $\Rightarrow$ c) Weźmy dowolny domknięty zbiór $F\subseteq E$ . Dla każdego $\varepsilon>0$ zbiór $F_{\varepsilon}=\{ x:\rho(x,F)\leq\varepsilon\}$ jest domknięty. Ponadto, zbiór $\{\varepsilon>0:P(\{ x:\rho(x,F)=\varepsilon\})>0\}$ jest co najwyżej przeliczalny; zatem istnieje ciąg $(\varepsilon _{n})$ liczb dodatnich malejący do $0$ taki, że $P(\{ x:\rho(x,F)=\varepsilon _{n}\})=0$ dla każdego $n$ . Ponieważ $\partial F_{\varepsilon}\subseteq\{ x:\rho(x,F)=\varepsilon\}$ , mamy więc $P(\partial F_{{\varepsilon _{n}}})=0$ dla każdego $n$ , a zatem, korzystając z e), przy ustalonym $k$ ,

$\limsup _{n}P_{n}(F)\leq\limsup _{n}P_{n}(F_{{\varepsilon _{k}}})=P(F_{{\varepsilon _{k}}}).$

Zbiegając z $k\to\infty$ , mamy $\varepsilon _{k}\to 0$ oraz $P(F_{{\varepsilon _{k}}})\to P(F)$ , na mocy tego, iż $F$ jest domknięty.

∎

Stwierdzenie 1.2

Załóżmy, że $P_{n}$ , $P$ są rozkładami prawdopodobieństwa w $\mathbb{R}^{d}$ ( $n=1,\, 2,\,\ldots$ ), o dystrybuantach $F_{n}$ , $F$ , odpowiednio. Wówczas $P_{n}\Rightarrow P$ wtedy i tylko wtedy, gdy $F_{n}(x)\to F(x)$ dla każdego punktu $x$ , w którym $F$ jest ciągła.

Dowód:

$\Rightarrow$ Weźmy punkt $x=(x_{1},\, x_{2},\,\ldots,\, x_{d})$ ciągłości dystrybuanty $F$ i niech $A=\{ y\in\mathbb{R}^{d}:y_{i}\leq x_{i},\, i=1,\, 2,\,\ldots,\, d\}$ . Zauważmy, iż $P(\partial A)=0$ ; w przeciwnym razie $F$ miałaby nieciągłość w punkcie $x$ (istotnie, mielibyśmy

$\begin{split}\lim _{{k\to\infty}}F(x_{1}-\frac{1}{k},x_{2}-\frac{1}{k},\ldots,\, x_{d}-\frac{1}{k})&=\lim _{{k\to\infty}}P(\{ y\in\mathbb{R}^{d}:y_{i}\leq x_{i}-\frac{1}{k}\})\\ &<P(A)=F(x)\,).\end{split}$

Zatem na mocy podpunktu e) Twierdzenia 1.1, $F_{n}(x)=P_{n}(A)\to P(A)=F(x)$ .

$\Leftarrow$ Najpierw udowodnimy

Lemat 1.2

Załóżmy, że $E$ jest przestrzenią metryczną, $\mathcal{K}\subseteq\mathcal{B}(E)$ jest $\pi$ -układem takim, że każdy zbiór otwarty jest sumą skończoną lub przeliczalną zbiorów z $\mathcal{K}$ . Jeśli $P_{n}$ , $P$ ( $n=1,\, 2,\,\ldots$ ) są miarami probabilistycznymi na $\mathcal{B}(E)$ takimi, że dla każdego $A\in\mathcal{K}$ mamy $P_{n}(A)\to P(A)$ , to $P_{n}\Rightarrow P$ .

Udowodnimy, że dla każdego zbioru otwartego $G\subseteq E$ , $\liminf P_{n}(G)\geq P(G)$ . Ustalmy więc zbiór otwarty $G$ oraz $\varepsilon>0$ . Z założeń lematu istnieje skończony ciąg $A_{1},\, A_{2},\,\ldots,\, A_{k}$ elementów $\mathcal{K}$ taki, że

$A_{1}\cup A_{2}\cup\ldots\cup A_{k}\subseteq G,\,\text{ oraz }\, P(G\setminus(A_{1}\cup A_{2}\cup\ldots\cup A_{k}))<\varepsilon.$

Mamy $P(G\setminus(A_{1}\cup A_{2}\cup\ldots\cup A_{k}))=P(G)-P(A_{1}\cup A_{2}\cup\ldots\cup A_{k})$ , skąd, na mocy wzoru włączeń i wyłączeń,

$\begin{split} P(G)&<\varepsilon+P(\bigcup _{{i=1}}^{k}A_{i})=\varepsilon+\sum _{{i=1}}^{k}P(A_{i})-\sum _{{1\leq i<j\leq k}}P(A_{i}\cap A_{j})+\ldots\\ &=\varepsilon+\sum _{{i=1}}^{k}\lim _{{n\to\infty}}P_{n}(A_{i})-\sum _{{1\leq i<j\leq k}}\lim _{{n\to\infty}}P_{n}(A_{i}\cap A_{j})+\ldots\\ &=\varepsilon+\lim _{n}P_{n}(\bigcup _{{i=1}}^{k}A_{i})\leq\varepsilon+\liminf _{n}P_{n}(G).\end{split}$

Wystarczy skorzystać z tego, że $\varepsilon>0$ było dowolne.

∎

Wracamy do dowodu stwierdzenia. Dla każdego $i=1,\, 2,\,\ldots$ istnieje co najwyżej przeliczalnie wiele hiperpłaszczyzn $H\subset\mathbb{R}^{d}$ prostopadłych do osi $OX_{i}$ , o dodatniej mierze $P$ ; niech $S$ oznacza dopełnienie sumy wszystkich takich hiperpłaszczyzn (sumujemy także po $i$ ). Jak łatwo zauważyć, $S$ jest gęstym podzbiorem $\mathbb{R}^{d}$ oraz każdy punkt z $S$ jest punktem ciągłości $F$ . Zbiór

$\mathcal{K}=\{(a,b]=(a_{1},b_{1}]\times(a_{2},b_{2}]\times\ldots(a_{d},b_{d}]:a,b\in S,\, a_{i}<b_{i}\text{ dla każdego }i\}$

jest $\pi$ -układem i każdy zbiór otwarty jest sumą skończoną lub przeliczalną zbiorów z $\mathcal{K}$ . Mamy

$\begin{split}&P_{n}((a,b])\\ &=\sum _{{\varepsilon _{i}\in\{ 0,1\}}}(-1)^{{d-(\varepsilon _{1}+\varepsilon _{2}+\ldots+\varepsilon _{d})}}F_{n}(b_{1}+\varepsilon _{1}(b_{1}-a_{1}),\ldots,b_{d}+\varepsilon _{d}(b_{d}-a_{d}))\\ &\to\sum _{{\varepsilon _{i}\in\{ 0,1\}}}(-1)^{{d-(\varepsilon _{1}+\varepsilon _{2}+\ldots+\varepsilon _{d})}}F(b_{1}+\varepsilon _{1}(b_{1}-a_{1}),\ldots,b_{d}+\varepsilon _{d}(b_{d}-a_{d}))\\ &=P((a,b]).\end{split}$

Wystarczy skorzystać z poprzedniego lematu.

∎

Definicja 1.2

Załóżmy, że $X_{n}$ , $X$ ( $n=1,\, 2,\,\ldots$ ) są zmiennymi losowymi o wartościach w $E$ oraz $\mu$ jest miarą probabilistyczną na $\mathcal{B}(E)$ .

(i) Mówimy, że ciąg $(X_{n})$ jest zbieżny według rozkładu do $X$ , jeśli $P_{{X_{n}}}\Rightarrow P_{{X}}$ . Oznaczenie: $X_{n}\Rightarrow X$ lub $X_{n}\xrightarrow{\mathcal{D}}X$ .

(ii) Mówimy, że ciąg $(X_{n})$ jest zbieżny według rozkładu do $\mu$ , jeśli $P_{{X_{n}}}\Rightarrow\mu$ . Oznaczenie $X_{n}\Rightarrow\mu$ lub $X_{n}\xrightarrow{\mathcal{D}}\mu$ .

Uwagi:

W definicji zbieżności według rozkładu, zmienne 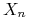$X_{n}$ mogą być określone na różnych przestrzeniach probabilistycznych.
Równoważnie, $(X_{n})$ zbiega do $X$ według rozkładu wtedy i tylko wtedy, gdy dla każdej funkcji $f\in C(E)$ ,

$\lim _{{n\to\infty}}\mathbb{E}f(X_{n})=\mathbb{E}f(X).$ (1.2)

Ponadto, na mocy podpunktu b) Twierdzenia 1.1, można się ograniczyć w (1.2) do funkcji jednostajnie ciągłych.
Słaba zbieżność odnosi się wyłącznie do rozkładów zmiennych losowych. Na przykład, rozważmy ciąg 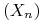$(X_{n})$ , zadany na przestrzeni probabilistycznej $([0,1],\mathcal{B}([0,1]),|\cdot|)$ wzorem

$X_{{2n-1}}=1_{{[0,1/2]}},\,\,\,\, X_{{2n}}=1_{{[1/2,1]}},\,\qquad n=1,\, 2,\,\ldots.$

Jak łatwo zauważyć, 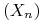$(X_{n})$ nie jest ani zbieżny prawie na pewno, ani według prawdopodobieństwa. Natomiast z punktu widzenia słabej zbieżności, jest to ciąg stały: 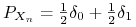$P_{{X_{n}}}=\frac{1}{2}\delta _{0}+\frac{1}{2}\delta _{1}$ . Ciąg ten zbiega słabo do 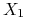$X_{1}$ oraz do $X_{2}$ .

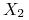Stwierdzenie 1.3

Załóżmy, że $E$ jest przestrzenią ośrodkową oraz $X$ , $X_{n}$ , $Y_{n}$ ( $n=1,\, 2,\,\ldots$ ) są zmiennymi losowymi o wartościach w $E$ , przy czym dla każdego $n$ , zmienne $X_{n}$ oraz $Y_{n}$ są określone na tej samej przestrzeni probabilistycznej. Jeśli $X_{n}\Rightarrow X$ oraz $\rho(X_{n},Y_{n})\xrightarrow{\mathbb{P}}0$ , to $Y_{n}\Rightarrow X$ .

Biorąc $X_{n}=X$ , dostajemy stąd natychmiast następujący fakt.

Wniosek 1.1

Jeśli $(X_{n})$ zbiega do $X$ według prawdopodobieństwa, to zbiega także według rozkładu.

Dowód Stwierdzenia 1.3

Niech $F$ będzie dowolnym domkniętym podzbiorem przestrzeni $E$ i ustalmy $\varepsilon>0$ . Zbiór $F_{\varepsilon}=\{ x:\rho(x,F)\leq\varepsilon\}$ jest domknięty i mamy

$\begin{split} P_{{Y_{n}}}(F)&=\mathbb{P}(Y_{n}\in F,\,\rho(X_{n},Y_{n})\leq\varepsilon)+\mathbb{P}(Y_{n}\in F,\,\rho(X_{n},Y_{n})>\varepsilon)\\ &\leq\mathbb{P}(X_{n}\in F_{\varepsilon})+\mathbb{P}(\rho(X_{n},Y_{n})>\varepsilon).\end{split}$

Zatem

$\limsup _{n}P_{{Y_{n}}}(F)\leq\limsup _{n}P_{{X_{n}}}(F_{\varepsilon})+0\leq P_{X}(F_{\varepsilon})$

i przechodząc z $\varepsilon$ do $0$ dostajemy $\limsup _{n}P_{{Y_{n}}}(F)\leq P_{X}(F)$ . Z dowolności $F$ oraz podpunktu c) Twierdzenia 1.1 wynika teza.

∎

Definicja 1.3

Niech $\mathcal{P}$ będzie pewnym zbiorem miar probabilistycznych na $\mathcal{B}(E)$ . Mówimy, że ten zbiór jest ciasny (jędrny) jeśli dla każdego $\varepsilon>0$ istnieje zwarty podzbiór $K$ przestrzeni $E$ taki, że $P(K)\geq 1-\varepsilon$ dla każdego $P\in\mathcal{P}$ .

Przykład:

Załóżmy, że $(X_{i})_{{i\in\mathcal{I}}}$ jest rodziną zmiennych losowych o wartościach rzeczywistych, takich, że dla pewnego $\alpha>0$ , $a:=\sup _{{i\in\mathcal{I}}}\mathbb{E}|X_{i}|^{\alpha}<\infty$ . Wówczas rodzina rozkładów $(P_{{X_{i}}})_{{i\in\mathcal{I}}}$ jest ciasna. Istotnie, ustalmy $\varepsilon>0$ i $L>0$ . Na mocy nierówności Czebyszewa, dla każdego $i\in\mathcal{I}$ ,

$P_{{X_{i}}}([-L,L])=\mathbb{P}(|X_{i}|\leq L)=1-\mathbb{P}(|X_{i}|>L)\geq 1-\frac{\mathbb{E}|X_{i}|^{\alpha}}{L^{\alpha}}\geq 1-\frac{a}{L^{\alpha}}=1-\varepsilon,$

o ile $a/L^{\alpha}=\varepsilon$ ; wystarczy więc wziąć $K=[-(a/\varepsilon)^{{1/\alpha}},(a/\varepsilon)^{{1/\alpha}}]$ .

Twierdzenie 1.2 (Prochorow)

(i) (Twierdzenie odwrotne) Jeśli $\mathcal{P}$ jest zbiorem ciasnym, to z każdego ciągu elementów $\mathcal{P}$ można wybrać podciąg zbieżny.

(ii) (Twierdzenie proste) Jeśli $E$ jest przestrzenią polską (tzn. ośrodkową i zupełną) i $\mathcal{P}$ ma tę własność, że z każdego ciągu można wybrać podciąg zbieżny, to $\mathcal{P}$ jest zbiorem ciasnym.

Potrzebne nam będą następujące trzy fakty: z Topologii, Analizy Funkcjonalnej oraz Teorii Miary.

Stwierdzenie 1.4

Załóżmy, że $K$ jest przestrzenią metryczną zwartą. Wówczas $C(K)$ jest ośrodkowa.

Twierdzenie 1.3 (Riesz)

Załóżmy, że $\varphi:C(K)\to\mathbb{R}$ jest dodatnim funkcjonałem liniowym ciągłym, tzn.

(i) $\varphi(af+bg)=a\varphi(f)+b\varphi(g)$ dla dowolnych $a,\, b\in\mathbb{R}$ , $f,\, g\in C(K)$ .

(ii) Istnieje stała $L$ taka, że $|\varphi(f)|\leq L\sup _{{x\in K}}|f(x)|$ dla wszystkich $f\in C(K)$ .

(iii) Dla dowolnej nieujemnej funkcji $f\in C(K)$ mamy $\varphi(f)\geq 0$ .
Wówczas istnieje dokładnie jedna miara skończona $\lambda$ na $\mathcal{B}(K)$ taka, że $\varphi(f)=\int _{K}f(x)\lambda(dx)$ dla dowolnej funkcji $f\in C(K)$ .

Stwierdzenie 1.5 (Regularność)

Załóżmy, że $\mu$ jest miarą skończoną na $\mathcal{B}(E)$ . Wówczas dla każdego $A\in\mathcal{B}(E)$ istnieje ciąg $(F_{n})$ zbiorów domkniętych zawartych w $A$ oraz ciąg $(G_{n})$ zbiorów otwartych zawierających $A$ , takie, że $\mu(F_{n})\xrightarrow{n\to\infty}\mu(A)$ oraz $\mu(G_{n})\xrightarrow{n\to\infty}\mu(A)$ .

Dowód twierdzenia odwrotnego

Załóżmy, że $\mathcal{P}$ jest ciasny. Wobec tego, dla każdego $m=1,\, 2,\,\ldots$ istnieje zwarty podzbiór $K_{m}$ przestrzeni $E$ taki, że $P(K_{m})\geq 1-\frac{1}{m}$ dla wszystkich $P\in\mathcal{P}$ . Bez straty ogólności możemy założyć, że ciąg $(K_{m})$ jest wstępujący (zastępując ten ciąg, w razie potrzeby, przez ciąg $K_{1},\, K_{1}\cup K_{2},\, K_{1}\cup K_{2}\cup K_{3},\,\ldots$ ).

Niech $(P_{m})$ będzie ciągiem miar z $\mathcal{P}$ . Dla większej przejrzystości dowodu, podzielimy go na kilka części.

1. Na mocy Stwierdzenia 1.4, dla każdego $m=1,\, 2,\,\ldots$ , $C(K_{m})$ jest przestrzenią ośrodkową. Niech $\{ f_{{m_{r}}}\} _{{r=1,\, 2,\,\ldots}}$ będzie jej przeliczalnym gęstym podzbiorem. Dla każdego $m,\, r$ , ciąg $(\int _{{K_{m}}}f_{{m_{r}}}dP_{n})_{n}$ jest ograniczonym ciągiem liczbowym; można z niego wybrać podciąg zbieżny. Stosując metodę przekątniową widzimy, iż istnieje podciąg $(n_{1},n_{2},\ldots)$ taki, że dla wszystkich $m,\, r$ , ciąg $(\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{i}}})_{i}$ jest zbieżny.

2. Pokażemy, że dla każdego $m=1,\, 2,\,\ldots$ i każdej funkcji $f\in C(K_{m})$ , ciąg $(\int _{{K_{m}}}fdP_{{n_{i}}})_{i}$ jest zbieżny. Ustalmy $\varepsilon>0$ oraz $r$ takie, że $\sup _{{x\in K_{m}}}|f(x)-f_{{m_{r}}}(x)|\leq\varepsilon/3$ . Mamy

$\begin{split}\left|\int _{{K_{m}}}fdP_{{n_{i}}}-\int _{{K_{m}}}fdP_{{n_{j}}}\right|&\leq\left|\int _{{K_{m}}}fdP_{{n_{i}}}-\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{i}}}\right|\\ &+\left|\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{i}}}-\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{j}}}\right|\\ &+\left|\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{j}}}-\int _{{K_{m}}}fdP_{{n_{j}}}\right|.\end{split}$

Dwa skrajne składniki po prawej stronie szacują się przez $\varepsilon/3$ ; na przykład, mamy

$\begin{split}\left|\int _{{K_{m}}}fdP_{{n_{i}}}-\int _{{K_{m}}}f_{{m_{r}}}dP_{{n_{i}}}\!\right|&\leq\int _{{K_{m}}}|f-f_{{m_{r}}}|dP_{{n_{i}}}\\ &\leq\sup _{K}|f-f_{{m_{r}}}|P_{{n_{i}}}(K_{m})\leq\varepsilon/3.\end{split}$

środkowy składnik nie przekracza $\varepsilon/3$ o ile $i$ , $j$ są dostatecznie duże; wynika to z definicji podciągu $(n_{i})$ .

3. Oznaczmy $\varphi _{m}(f)=\lim _{{i\to\infty}}\int _{{K_{m}}}fdP_{{n_{i}}}$ , dla $f\in C(K_{m})$ . Jest oczywiste, że $\varphi$ spełnia założenia Twierdzenia Riesza. Zatem istnieje miara $\lambda _{m}$ na $\mathcal{B}(K_{m})$ taka, że $\varphi _{m}(f)=\int _{{K_{m}}}fd\lambda _{m}$ dla wszystkich $f\in C(K_{m})$ , $m=1,\, 2,\,\ldots$ . Rozszerzmy tę miarę na $\mathcal{B}(E)$ , kładąc $\lambda _{m}(A)=\lambda _{m}(A\cap K_{m})$ .

4. Udowodnimy, że dla każdego $A\in\mathcal{B}(E)$ ciąg $(\lambda _{m}(A))$ spełnia warunek Cauchy'ego. ściślej, wykażemy, że

$0\leq\lambda _{{m_{1}}}(A)-\lambda _{{m_{2}}}(A)\leq\frac{1}{m_{2}}\qquad\text{ dla }m_{1}>m_{2}\geq 1.$

(1.3)

Najpierw załóżmy, że $F$ jest zbiorem domkniętym i niech $\varepsilon>0$ . Niech $f_{\varepsilon}$ będzie nieujemną funkcją jednostajnie ciągłą pochodzącą z Lematu 1.1. Mamy

$\begin{split} 0&\leq\int _{{K_{{m_{1}}}\setminus K_{{m_{2}}}}}f_{\varepsilon}dP_{{n_{i}}}=\int _{{K_{{m_{1}}}}}f_{\varepsilon}dP_{{n_{i}}}-\int _{{K_{{m_{2}}}}}f_{\varepsilon}dP_{{n_{i}}}\\ &\leq\sup _{{E}}|f_{\varepsilon}|(P_{{n_{i}}}(K_{{m_{1}}})-P_{{n_{i}}}(K_{{m_{2}}}))\leq 1-P_{{n_{i}}}(K_{{m_{2}}})\leq\frac{1}{m_{2}}.\end{split}$

Zbiegając teraz z $i$ do nieskończoności dostajemy

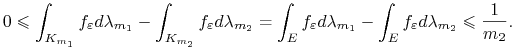$0\leq\int _{{K_{{m_{1}}}}}f_{\varepsilon}d\lambda _{{m_{1}}}-\int _{{K_{{m_{2}}}}}f_{\varepsilon}d\lambda _{{m_{2}}}=\int _{{E}}f_{\varepsilon}d\lambda _{{m_{1}}}-\int _{{E}}f_{\varepsilon}d\lambda _{{m_{2}}}\leq\frac{1}{m_{2}}.$

Weźmy teraz $\varepsilon\to 0$ ; ponieważ $f_{\varepsilon}\to 1_{A}$ , otrzymujemy (1.3) dla zbiorów domkniętych, na mocy twierdzenia Lebesgue'a. Aby otrzymać tę nierówność w przypadku ogólnym, posłużymy się regularnością. Dla dowolnego $A\in\mathcal{B}(E)$ istnieją ciągi $(F_{k}^{{\prime}})$ oraz $(F_{k}^{{\prime\prime}})$ zbiorów domkniętych zawartych w $A$ , takie, że $\lambda _{{m_{1}}}(F_{k}^{{\prime}})\to\lambda _{{m_{1}}}(A)$ oraz $\lambda _{{m_{2}}}(F_{k}^{{\prime\prime}})\to\lambda _{{m_{2}}}(A)$ . Korzystając z (1.3) dla zbioru domkniętego $F_{k}=F_{k}^{{\prime}}\cup F_{k}^{{\prime\prime}}$ i zbiegając z $k\to\infty$ otrzymujemy żądaną nierówność.

5. Wiemy, na mocy poprzedniej części, że ciąg $(\lambda _{m}(A))_{m}$ jest zbieżny dla każdego $A\in\mathcal{B}(E)$ . Oznaczmy jego granicę przez $\lambda(A)$ . Wykażemy, że $\lambda$ jest miarą probabilistyczną oraz $P_{{n_{i}}}\Rightarrow\lambda$ . Pierwsza własność wyniknie z następujących trzech faktów.

a) $\lambda(E)=1$ .

b) $\lambda(A_{1}\cup A_{2})=\lambda(A_{1})+\lambda(A_{2})$ dla $A_{1},\, A_{2}\in\mathcal{B}(E)$ takich, że $A_{1}\cap A_{2}=\emptyset.$

c) Jeśli $A_{1}\supseteq A_{2}\supseteq\ldots$ oraz $\bigcap _{{k=1}}^{\infty}A_{k}=\emptyset$ , to $\lambda(A_{k})\to 0$ .

Dowód a) Mamy $1\geq P_{{n_{i}}}(K_{m})=\int _{{K_{m}}}1dP_{{n_{i}}}\geq 1-\frac{1}{m}$ . Zbiegając z $i$ do nieskończoności dostajemy $1\geq\lambda _{m}(E)\geq 1-\frac{1}{m}$ , i teraz dążąc z $m$ do nieskończoności otrzymujemy $\lambda(E)=1$ .

Dowód b) Jasne na mocy definicji $\lambda$ i tego, że $\lambda _{m}$ jest miarą dla każdego $m$ .

Dowód c) Na mocy (1.3), mamy $0\leq\lambda(A)-\lambda _{m}(A)\leq\frac{1}{m}$ dla wszystkich $A\in\mathcal{B}(E)$ oraz $m=1,\, 2,\,\ldots$ . Zatem, dla dowolnego $k$ ,

$\lambda(A_{k})=\lambda(A_{k})-\lambda _{m}(A_{k})+\lambda _{m}(A_{k})\leq\frac{1}{m}+\lambda _{m}(A_{k}).$

Zbiegając z $k\to\infty$ widzimy, że $\limsup _{{k\to\infty}}\lambda(A_{k})\leq 1/m$ , co na mocy dowolności $m$ daje $\limsup _{k}\lambda(A_{k})=0$ , czyli $\lim _{{k\to\infty}}\lambda(A_{k})=0$ .

Pozostało już tylko sprawdzić, że $P_{{n_{i}}}\Rightarrow\lambda$ . Dla usalonej $f\in C(E)$ , mamy

$\begin{split}\left|\int _{E}fdP_{{n_{i}}}-\int _{E}fd\lambda\right|\leq&\left|\int _{{K_{m}^{c}}}fdP_{{n_{i}}}\right|+\left|\int _{{K_{m}}}fdP_{{n_{i}}}-\int _{{K_{m}}}fd\lambda _{m}\right|\\ &+\left|\int _{E}fd\lambda _{m}-\int _{E}fd\lambda\right|=I+II+III.\end{split}$

Na mocy ciasności, $I\leq\sup _{E}|f|\cdot\frac{1}{m}$ . Ponadto, z definicji $\lambda _{m}$ , $II\to 0$ gdy $m\to\infty$ . Wreszcie,

$III=\left|\int _{E}fd(\lambda-\lambda _{m})\right|\leq\sup _{E}|f|(\lambda(E)-\lambda _{m}(E))\leq\sup _{E}|f|\cdot\frac{1}{m}.$

Zatem $I+II+III\to 0$ gdy $m\to\infty$ . Dowód jest zakończony.

∎

Dowód prostego twierdzenia Prochorowa jest znacznie łatwiejszy i pozostawiamy go jako ćwiczenie (patrz zadanie 13).

Na zakończenie, zaprezentujemy następujące dwa fakty (bez dowodu).

Twierdzenie 1.4 (Skorochod)

Załóżmy, że $E$ jest przestrzenią ośrodkową oraz $P_{n}$ , $P$ ( $n=1,\, 2,\,\ldots$ ) są miarami probabilistycznymi na $\mathcal{B}(E)$ . Jeśli $P_{n}\Rightarrow P$ , to istnieją zmienne losowe $X_{n}$ , $X$ ( $n=1,\, 2,\,\ldots$ ), określone na tej samej przestrzeni probabilistycznej $(\Omega,\mathcal{F},\mathbb{P})$ takie, że $P_{{X_{n}}}=P_{n}$ , $P_{X}=P$ ( $n=1,\, 2\,\ldots$ ) oraz $X_{n}\to X$ prawie na pewno.

Twierdzenie 1.5

Załóżmy, że $E$ jest przestrzenią ośrodkową i niech $\mathcal{M}$ oznacza klasę wszystkich miar probabilistycznych na $E$ . Dla $P,\, Q\in\mathcal{M}$ definiujemy

$\pi(P,Q)=\inf\{\varepsilon>0:\forall _{{A\in\mathcal{B}(E)}}\,\, Q(A)\leq P(A_{\varepsilon})+\varepsilon,\, P(A)\leq Q(A_{\varepsilon})+\varepsilon\}.$

Wówczas $\pi$ jest metryką w $\mathcal{M}$ (jest to tzw. metryka Levy-Prochorowa) oraz zbieżność w sensie tej metryki pokrywa się ze zwykłą zbieżnością miar probabilistycznych.

1.1. Zadania

1. Udowodnić, że ciąg $(\text{Exp}(n/(n+1)))$ jest zbieżny według rozkładu do Exp $(1)$ .

2. Dany jest ciąg $(X_{n})$ zmiennych losowych zbieżny według rozkładu do zmiennej losowej $X$ . Udowodnić, że ciąg $(\sin X_{n})$ jest zbieżny według rozkładu do zmiennej $\sin X$ .

3. Czy zmienne losowe posiadające gęstość mogą zbiegać według rozkładu do zmiennej o rozkładzie dyskretnym? Czy zmienne losowe o rozkładach dyskretnych mogą zbiegać do zmiennej o rozkładzie ciągłym?

4. Niech $X_{1},\ X_{2},\ \ldots$ będą zmiennymi losowymi, przy czym dla $n\geq 1$ rozkład zmiennej $X_{n}$ określony jest następująco:

$\mathbb{P}\left(X_{n}=\frac{j}{n}\right)=\frac{2j}{n(n+1)},\ \ j=1,\ 2,\ \ldots,\ n.$

Udowodnić, że ciąg $(X_{n})$ jest zbieżny według rozkładu. Wyznaczyć rozkład graniczny.

5. Niech $B(n,p)$ oznacza rozkład Bernoulliego o $n$ próbach z prawdopodobieństwem sukcesu $p$ , a $\text{Pois}(\lambda)$ - rozkład Poissona z parametrem $\lambda$ . Wykazać, że jeśli $np_{n}\to\lambda$ , to $B(n,p_{n})\Rightarrow Pois(\lambda)$ .

6. Zmienne losowe $X_{1},\ X_{2},\ \ldots$ zbiegają według rozkładu do zmiennej $X$ stałej p.n. Wykazać, że ciąg $(X_{n})$ zbiega do $X$ według prawdopodobieństwa.

7. Niech $g_{n}$ , $g$ oznaczają odpowiednio gęstości rozkładów prawdopodobieństwa $\mu _{n}$ , $\mu$ na $\mathbb{R}^{N}$ . Udowodnić, że jeśli $g_{n}\to g$ p.w., to $\mu _{n}\Rightarrow\mu$ .

8. Niech $S$ będzie przeliczalnym podzbiorem $\mathbb{R}^{N}$ , zaś $\mu _{n}$ , $\mu$ - miarami probabilistycznymi skupionymi na $S$ . Wykazać, że jeśli dla każdego $x\in S$ mamy $\mu _{n}(\{ x\})\to\mu(\{ x\})$ , to $\mu _{n}\Rightarrow\mu$ .

9. Ciąg dystrybuant $(F_{n})$ zbiega punktowo do dystrybuanty ciągłej $F$ . Wykazać, że zbieżność jest jednostajna.

10. Dane są ciągi $(X_{n})$ , $(Y_{n})$ zmiennych losowych, określonych na tej samej przestrzeni probabilistycznej, przy czym $(X_{n})$ zbiega według rozkładu do $X$ , a $(Y_{n})$ zbiega według rozkładu do zmiennej $Y$ stałej p.n.. Udowodnić, że $(X_{n}+Y_{n})$ zbiega według rozkładu do $X+Y$ . Czy teza pozostaje prawdziwa bez założenia o jednopunktowym rozkładzie $Y$ ?

11. Dany jest ciąg $(X_{n})$ zmiennych losowych przyjmujących wartości w przedziale $[0,1]$ . Udowodnić, że jeśli dla każdego $k=0,\, 1,\, 2,\,\ldots$ mamy $\mathbb{E}X_{n}^{k}\xrightarrow{n\to\infty}\frac{1}{k+1}$ , to $(X_{n})$ jest zbieżny według rozkładu.

12. Załóżmy, że $(X_{n})$ jest ciągiem niezależnych zmiennych losowych o rozkładzie Cauchy'ego z parametrem $a>0$ , tzn. z gęstością

$g(x)=\frac{a}{\pi(a^{2}+x^{2})}.$

Udowodnić, że $\frac{1}{n}\max _{{k\leq n}}X_{k}\Rightarrow\frac{1}{T}$ , gdzie $T$ ma rozkład wykładniczy. Wyznaczyć parametr tego rozkładu.

13. Załóżmy, że $E$ jest przestrzenią polską oraz $\mathcal{P}$ jest rodziną miar probabilistycznych na $\mathcal{B}(E)$ , taką, że z każdego ciągu jej elementów można wybrać podciąg zbieżny.

(i) Udowodnić, że

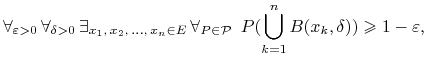$\forall _{{\varepsilon>0}}\,\forall _{{\delta>0}}\,\exists _{{x_{1},\, x_{2},\,\ldots,\, x_{n}\in E}}\,\forall _{{P\in\mathcal{P}}}\,\,\, P(\bigcup _{{k=1}}^{n}B(x_{k},\delta))\geq 1-\varepsilon,$

gdzie $B(x,\delta)=\{ y\in E:\rho(x,y)<\delta\}$ .

(ii) Wywnioskować z (i) proste twierdzenie Prochorowa (wskazówka: w przestrzeni metrycznej zupełnej zbiór domknięty i całkowicie ograniczony - tzn. dla każdego $\varepsilon>0$ posiadający skończoną $\varepsilon$ -sieć - jest zwarty).

14. Załóżmy, że ciąg $(X_{n})$ zbiega według rozkładu do $X$ . Niech $h:\mathbb{R}\to\mathbb{R}$ będzie taką funkcją borelowską, że $\mathbb{P}(X\in\{\text{punkty nieciągłości }h\})=0$ .

(i) Udowodnić, że $h(X_{n})\Rightarrow h(X)$ .

(ii) Udowodnić, że jeśli $h$ jest dodatkowo ograniczona, to $\mathbb{E}h(X_{n})\xrightarrow{n\to\infty}\mathbb{E}h(X)$ .

15. Załóżmy, że ciąg $(X_{n})$ zbiega według rozkładu do $X$ . Udowodnić, że

(i) $E|X|\leq\liminf _{n}\mathbb{E}|X_{n}|$ .

(ii) jeśli $X_{1},\, X_{2},\,$ są dodatkowo jednostajnie całkowalne, to $\mathbb{E}X_{n}\to\mathbb{E}X$ .

(iii) jeśli $X$ , $X_{1}$ , $X_{2}$ , $\ldots$ są calkowalne, nieujemne i $\mathbb{E}X_{n}\xrightarrow{n\to\infty}\mathbb{E}X$ , to $X_{1},\, X_{2},\,\ldots$ są jednostajnie całkowalne.