Zagadnienia
2. Funkcje charakterystyczne rozkładów prawdopodobieństwa w 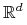
Do tej pory zajmowaliśmy się zmiennymi losowymi o wartościach w ![]() bądź, ogólniej, w przestrzeniach metrycznych (bez żadnej dodatkowej struktury). W tym rozdziale ważną rolę będą pełniły zmienne losowe o wartościach w
bądź, ogólniej, w przestrzeniach metrycznych (bez żadnej dodatkowej struktury). W tym rozdziale ważną rolę będą pełniły zmienne losowe o wartościach w ![]() .
.
2.1. Zmienne losowe o wartościach zespolonych.
Załóżmy, że ![]() jest przestrzenią probabilistyczną. Funkcja
jest przestrzenią probabilistyczną. Funkcja ![]() jest zmienną losową, jeśli jest zmienną losową przy utożsamieniu
jest zmienną losową, jeśli jest zmienną losową przy utożsamieniu ![]() - innymi słowy, jeśli
- innymi słowy, jeśli ![]() jest zmienną losową w
jest zmienną losową w ![]() . Jeśli
. Jeśli ![]() oraz
oraz ![]() są całkowalne (co jest równoważne temu, że
są całkowalne (co jest równoważne temu, że ![]() ), to definiujemy
), to definiujemy ![]() . Bez trudu dowodzimy, iż mają miejsce następujące fakty.
. Bez trudu dowodzimy, iż mają miejsce następujące fakty.
(i) Mamy ![]() .
.
(ii) Zachodzi twierdzenie Lebesgue'a o zmajoryzowanym przejściu do granicy pod znakiem wartości oczekiwanej.
(iii) Dla dowolnych ![]() i dowolnych zespolonych zmiennych losowych
i dowolnych zespolonych zmiennych losowych ![]() takich, że
takich, że ![]() istnieją, mamy
istnieją, mamy
2.2. Funkcje charakterystyczne
Przechodzimy do definicji głownego pojęcia tego rozdziału.
Definicja 2.1
(i) Załóżmy, że ![]() jest rozkładem prawdopodobieństwa w
jest rozkładem prawdopodobieństwa w ![]() . Funkcję
. Funkcję
nazywamy funkcją charakterystyczną ![]() .
.
(ii) Załóżmy, że ![]() jest zmienną losową o wartościach w
jest zmienną losową o wartościach w ![]() , określoną na
, określoną na ![]() . Wówczas
. Wówczas ![]() nazywamy funkcją charakterystyczną (rozkładu) zmiennej losowej
nazywamy funkcją charakterystyczną (rozkładu) zmiennej losowej ![]() .
.
Uwaga: Z twierdzenia o zamianie zmiennych wynika, iż ![]()
Bezpośrednio z definicji widzimy, że funkcja charakterystyczna zmiennej losowej zależy tylko od rozkładu tej zmiennej.
Własności funkcji charakterystycznych.
1) Załóżmy, że ![]() jest
jest ![]() -wymiarową zmienną losową. Wówczas
-wymiarową zmienną losową. Wówczas ![]() jest dobrze określona na całym
jest dobrze określona na całym ![]() , ponadto
, ponadto ![]() oraz
oraz
2) Załóżmy, że ![]() jest
jest ![]() -wymiarową zmienną losową. Wówczas
-wymiarową zmienną losową. Wówczas ![]() jest jednostajnie ciągła na
jest jednostajnie ciągła na ![]() ; istotnie, dla
; istotnie, dla ![]() ,
,
gdy ![]() .
.
3) Załóżmy, że ![]() jest
jest ![]() -wymiarową zmienną losową. Wówczas
-wymiarową zmienną losową. Wówczas ![]() jest dodatnio określona, tzn. dla wszystkich
jest dodatnio określona, tzn. dla wszystkich
![]() oraz
oraz ![]() ,
,
Istotnie, mamy
Powstaje naturalne pytanie: kiedy funkcja ![]() jest funkcją charakterystyczną pewnego rozkładu? Odpowiedź jest zawarta w
następującym twierdzeniu.
jest funkcją charakterystyczną pewnego rozkładu? Odpowiedź jest zawarta w
następującym twierdzeniu.
Twierdzenie 2.1 (Bochner)
Funkcja ![]() jest funkcją charakterystyczną pewnego rozkładu prawdopodobieństwa w
jest funkcją charakterystyczną pewnego rozkładu prawdopodobieństwa w ![]() wtedy i tylko wtedy, gdy jest ciągła, dodatnio określona oraz
wtedy i tylko wtedy, gdy jest ciągła, dodatnio określona oraz ![]() .
.
4) Załóżmy, że ![]() jest
jest ![]() -wymiarową zmienną losową,
-wymiarową zmienną losową, ![]() jest macierzą
jest macierzą ![]() oraz
oraz ![]() . Wówczas
. Wówczas
W szczególności, ![]() . Oznacza to, iż jeśli
. Oznacza to, iż jeśli ![]() (rozkład zmiennej jest symetryczny), to
(rozkład zmiennej jest symetryczny), to ![]() jest rzeczywista.
jest rzeczywista.
5) Załóżmy, że ![]() jest rzeczywistą zmienną losową taką, że
jest rzeczywistą zmienną losową taką, że ![]() dla pewnej liczby całkowitej dodatniej
dla pewnej liczby całkowitej dodatniej ![]() . Wówczas
. Wówczas ![]() ma
ma ![]() -tą pochodną ciągłą i
-tą pochodną ciągłą i
W szczególności, ![]() .
.
Weźmy najpierw ![]() . Mamy
. Mamy
Zauważmy, że ![]() oraz
oraz
zatem z twierdzenia Lebesgue'a wynika teza. Dla ![]() dowód jest analogiczny, opierający się na indukcji.
dowód jest analogiczny, opierający się na indukcji.
Zachodzi następujący ogólniejszy fakt: jeśli ![]() jest
jest ![]() -wymiarową zmienną losową taką, że
-wymiarową zmienną losową taką, że ![]() , to
, to ![]() ma ciągłe pochodne cząstkowe
ma ciągłe pochodne cząstkowe ![]() -tego rzędu i
-tego rzędu i
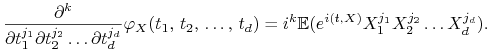 |
6) Jeśli zmienne ![]() ,
, ![]() ,
, ![]() ,
, ![]() są niezależne, to
są niezależne, to
Istotnie, mamy, iż ![]() są niezależne, skąd
są niezależne, skąd
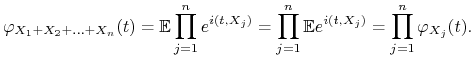 |
2.3. Przykłady.
(I) Załóżmy najpierw, że ![]() jest
jest ![]() -wymiarową zmienną losową o rozkładzie skokowym i niech
-wymiarową zmienną losową o rozkładzie skokowym i niech ![]() oznacza zbiór atomów. Bezpośrednio z definicji mamy, iż
oznacza zbiór atomów. Bezpośrednio z definicji mamy, iż
W szczególności:
1) Jeśli ![]() ,
, ![]() , to
, to ![]() . Co więcej, jeśli
. Co więcej, jeśli ![]() , to
, to ![]() .
.
2) Załóżmy, że ![]() Pois
Pois![]() ,
, ![]() . Mamy
. Mamy
 |
3) ![]() B
B![]() . Niech
. Niech ![]() będą niezależnymi zmiennymi losowymi o tym samym rozkładzie
będą niezależnymi zmiennymi losowymi o tym samym rozkładzie ![]() . Ponieważ
. Ponieważ ![]() ma ten sam rozkład co
ma ten sam rozkład co ![]() , to
, to
(II) Załóżmy teraz, że ![]() jest
jest ![]() -wymiarową zmienną losową o rozkładzie ciągłym z gęstością
-wymiarową zmienną losową o rozkładzie ciągłym z gęstością ![]() . Z definicji mamy, iż
. Z definicji mamy, iż
W szczególności:
4) Jeśli ![]() jest rozkładem jednostajnym na przedziale
jest rozkładem jednostajnym na przedziale ![]() , to
, to
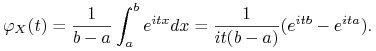 |
Jeśli ![]() , to
, to ![]() jest funkcją rzeczywistą i
jest funkcją rzeczywistą i ![]() .
.
5) Jeśli ![]() ,
, ![]() , to
, to
oraz
| (*) |
(w szczególności, dla standardowego rozkładu normalnego, dostajemy ![]() ).
).
Istotnie, weźmy ![]() jak wyżej. Zmienna
jak wyżej. Zmienna ![]() ma standardowy rozkład normalny i
ma standardowy rozkład normalny i
Zatem wystarczy udowodnić wzór (*) dla rozkładu ![]() . Załóżmy więc, że
. Załóżmy więc, że ![]() ma ten rozkład i zauważmy najpierw, że
ma ten rozkład i zauważmy najpierw, że ![]() jest funkcją rzeczywistą, gdyż rozkład
jest funkcją rzeczywistą, gdyż rozkład ![]() jest symetryczny. Zatem
jest symetryczny. Zatem
oraz
Dodatkowo, jak wiemy, ![]() : stąd
: stąd ![]() .
.
Ogólniej, jeśli ![]() ma
ma ![]() -wymiarowy rozkład normalny z gęstością
-wymiarowy rozkład normalny z gęstością
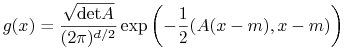 |
(gdzie ![]() to pewna macierz
to pewna macierz ![]() symetryczna i dodatnio określona, a
symetryczna i dodatnio określona, a ![]() jest pewnym wektorem z
jest pewnym wektorem z ![]() ), to
), to
Dowód tego faktu przeprowadzimy nieco później.
Przejdziemy teraz do twierdzenia o jednoznaczności: okazuje się, że funkcja charakterystyczna wyznacza rozkład jednoznacznie.
Twierdzenie 2.2 (O jednoznaczności)
Jeśli ![]() ,
, ![]() są rozkładami prawdopodobieństwa w
są rozkładami prawdopodobieństwa w ![]() takimi, że
takimi, że ![]() dla wszystkich
dla wszystkich ![]() , to
, to ![]() .
.
Zanim podamy dowód, najpierw sformułujmy wniosek.
Stwierdzenie 2.1
Zmienne losowe ![]() są niezależne wtedy i tylko wtedy, gdy
są niezależne wtedy i tylko wtedy, gdy
| (*) |
dla wszystkich ![]() .
.
Dowód:
![]() Mamy
Mamy
gdzie w przedostatnim przejściu korzystaliśmy z twierdzenia Fubiniego.
![]() Korzystając z przed chwilą udowodnionej implikacji, możemy zapisać (*) w postaci
Korzystając z przed chwilą udowodnionej implikacji, możemy zapisać (*) w postaci
a więc twierdzenie o jednoznaczności daje
czyli niezależność zmiennych ![]() .
.
W dowodzie twierdzenia o jednoznaczności będziemy potrzebować następującego pomocniczego faktu.
Twierdzenie 2.3 (Weierstrass)
Załóżmy, że ![]() jest ciągłą funkcją okresową. Wówczas istnieje ciąg
jest ciągłą funkcją okresową. Wówczas istnieje ciąg ![]() wielomianów trygonometrycznych o tym samym okresie co
wielomianów trygonometrycznych o tym samym okresie co ![]() , zbieżny jednostajnie do
, zbieżny jednostajnie do ![]() . (wielomian trygonometryczny o okresie
. (wielomian trygonometryczny o okresie ![]() to funkcja
to funkcja ![]() postaci
postaci ![]() )
)
Dowód twierdzenia o jednoznaczności (tylko dla 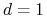 ):
):
Wystarczy udowodnić, że dla dowolnej funkcji ![]() mamy
mamy
| (*) |
Z założenia, (*) zachodzi dla funkcji ![]() ,
, ![]() , przy każdym ustalonym
, przy każdym ustalonym ![]() . Zatem, z liniowości, powyższa równość ma miejsce dla dowolnego wielomianu trygonometrycznego; mamy bowiem
. Zatem, z liniowości, powyższa równość ma miejsce dla dowolnego wielomianu trygonometrycznego; mamy bowiem ![]() ,
, ![]() . Na mocy twierdzenia Weierstrassa, (*) jest prawdziwa dla dowolnej funkcji ciągłej okresowej. Niech teraz
. Na mocy twierdzenia Weierstrassa, (*) jest prawdziwa dla dowolnej funkcji ciągłej okresowej. Niech teraz ![]() będzie dowolną funkcją ciągłą i ograniczoną. Istnieje ciąg
będzie dowolną funkcją ciągłą i ograniczoną. Istnieje ciąg ![]() funkcji ciągłych i okresowych o następującej własności:
funkcji ciągłych i okresowych o następującej własności:
Mamy, na mocy nierówności trójkąta,
gdy ![]() . Stąd otrzymujemy tezę. W przypadku ogólnym (tzn. dla
. Stąd otrzymujemy tezę. W przypadku ogólnym (tzn. dla ![]() ) dowód jest bardzo podobny; rolę twierdzenia Weierstrassa pełni ogólniejsze twierdzenie Stone'a-Weierstrassa.
) dowód jest bardzo podobny; rolę twierdzenia Weierstrassa pełni ogólniejsze twierdzenie Stone'a-Weierstrassa.
Rozkłady Gaussa (rozkłady normalne) w ![]() . Załóżmy, że
. Załóżmy, że ![]() ma rozkład normalny w
ma rozkład normalny w ![]() , o wartości ozekiwanej
, o wartości ozekiwanej ![]() i macierzy kowariancji
i macierzy kowariancji ![]() . Udowodnimy, że
. Udowodnimy, że
Istotnie, niech ![]() ,
, ![]() ,
, ![]() ,
, ![]() będą niezależnymi zmiennymi losowymi o standarowym rozkładzie normalnym na
będą niezależnymi zmiennymi losowymi o standarowym rozkładzie normalnym na ![]() i niech
i niech ![]() , gdzie
, gdzie ![]() jest macierzą
jest macierzą ![]() i
i ![]() . Mamy
. Mamy
Zauważmy, że ![]() jest macierzą symetryczną, nieujemnie określoną. Co więcej, każda macierz symetryczna
jest macierzą symetryczną, nieujemnie określoną. Co więcej, każda macierz symetryczna ![]() nieujemnie określona da się ta zapisać; stąd, dla dowolnej nieujemnie określonej symetrycznej macierzy
nieujemnie określona da się ta zapisać; stąd, dla dowolnej nieujemnie określonej symetrycznej macierzy ![]() o wymiarach
o wymiarach ![]() i dowolnego wektora
i dowolnego wektora ![]() , funkcja
, funkcja
jest funkcją charakterystyczną dokładnie jednego rozkładu prawdopodobieństwa w ![]() . Rozkłady tej postaci nazywamy rozkładami Gaussa w
. Rozkłady tej postaci nazywamy rozkładami Gaussa w ![]() . Zauważmy, że niektóre rozkłady Gaussa nie mają gęstości.
. Zauważmy, że niektóre rozkłady Gaussa nie mają gęstości.
Bezpośrednio z definicji dostajemy następujące wnioski.
Stwierdzenie 2.2
Załóżmy, że ![]() ma rozkład Gaussa w
ma rozkład Gaussa w ![]() , a
, a ![]() jest macierzą
jest macierzą ![]() i
i ![]() . Wówczas
. Wówczas ![]() ma rozkład Gaussa w
ma rozkład Gaussa w ![]() .
.
Stwierdzenie 2.3
Jeśli ![]() ,
, ![]() są niezależnymi zmiennymi losowymi o rozkładach Gaussa w
są niezależnymi zmiennymi losowymi o rozkładach Gaussa w ![]() o wartościach oczekiwanych
o wartościach oczekiwanych ![]() ,
, ![]() oraz macierzach kowariancji
oraz macierzach kowariancji ![]() ,
, ![]() , odpowiednio, to
, odpowiednio, to ![]() ma rozkład Gaussa w
ma rozkład Gaussa w ![]() o wartości średniej
o wartości średniej ![]() oraz macierzy
oraz macierzy ![]() .
.
Przechodzimy do kolejnego bardzo ważnego faktu, łączącego zbieżność według rozkładu ze zbieżnością funkcji charakterystycznych.
Twierdzenie 2.4 (Lévy - Cramera)
Załóżmy, że ![]() (
(![]() ) są rozkładami prawdopodobieństwa w
) są rozkładami prawdopodobieństwa w ![]() .
.
(i) Jeśli ![]() , to dla każdego
, to dla każdego ![]() ,
, ![]()
(ii) Jeśli dla każdego ![]() mamy
mamy ![]() , gdzie
, gdzie ![]() -pewna funkcja ciągła w
-pewna funkcja ciągła w ![]() , to
, to ![]() dla pewnego rozkładu
dla pewnego rozkładu ![]() i
i ![]() .
.
Dowód:
(i) Z definicji zbieżności według rozkładu mamy, dla dowolnego ![]() ,
,
(ii) Zacznijmy od pomocniczego faktu.
Lemat 2.1
Jeśli ![]() dla
dla ![]() należących do pewnego otoczenia
należących do pewnego otoczenia ![]() i
i ![]() jest ciągła w
jest ciągła w ![]() , to rodzina
, to rodzina ![]() jest ciasna.
jest ciasna.
Dowód lematu:
Wprowadźmy oznaczenie ![]() . Przypuśćmy, wbrew tezie, że rodzina
. Przypuśćmy, wbrew tezie, że rodzina ![]() nie jest ciasna. Wówczas istnieje
nie jest ciasna. Wówczas istnieje ![]() o tej własności, iż przy każdym
o tej własności, iż przy każdym ![]() mamy
mamy ![]() dla pewnego
dla pewnego ![]() . Zauważmy, iż
. Zauważmy, iż ![]() ; istotnie, w przeciwnym razie pewna liczba
; istotnie, w przeciwnym razie pewna liczba ![]() znalazłaby się w ciągu
znalazłaby się w ciągu ![]() nieskończenie wiele razy, co prowadziłoby do nierówności
nieskończenie wiele razy, co prowadziłoby do nierówności ![]() ; sprzeczność.
; sprzeczność.
Ponieważ ![]() jest ciągła w
jest ciągła w ![]() , to Re
, to Re![]() także ma tę własność; ponadto, na mocy zbieżności punktowej, Re
także ma tę własność; ponadto, na mocy zbieżności punktowej, Re![]() . Wobec tego istnieje takie
. Wobec tego istnieje takie ![]() , że dla każdego
, że dla każdego ![]() mamy
mamy ![]() oraz Re
oraz Re![]() . Dalej,
. Dalej,
gdzie
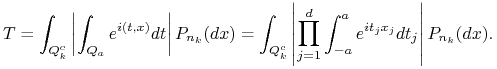 |
Ustalmy teraz ![]() . Istnieje współrzędna
. Istnieje współrzędna ![]() punktu
punktu ![]() większa co do modułu niż
większa co do modułu niż ![]() , zatem
, zatem
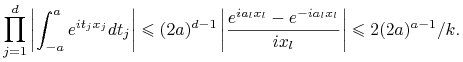 |
Stąd
Ale na mocy twierdzenia Lebesgue'a, ![]() ; stąd sprzeczność:
; stąd sprzeczność: ![]() .
.
Przechodzimy do dowodu części (ii) twierdzenia Levy-Cramera. Powyższy lemat oraz twierdzenie Prochorowa dają istnienie miary probabilistycznej ![]() na
na ![]() oraz podciągu
oraz podciągu ![]() zbieżnego słabo do
zbieżnego słabo do ![]() . Na mocy części (i) twierdzenia Levy-Cramera, mamy
. Na mocy części (i) twierdzenia Levy-Cramera, mamy ![]() , skąd
, skąd ![]() . Pozostaje jeszcze tylko udowodnić, że
. Pozostaje jeszcze tylko udowodnić, że ![]() . Przypuśćmy przeciwnie, iż dla pewnej funkcji
. Przypuśćmy przeciwnie, iż dla pewnej funkcji ![]() mamy
mamy ![]() ; stąd, dla pewnego podciągu
; stąd, dla pewnego podciągu ![]() ,
,
| (*) |
Ale na mocy lematu, rodzina ![]() także jest ciasna, stąd z twierdzenia Prochorowa istnieje podciąg
także jest ciasna, stąd z twierdzenia Prochorowa istnieje podciąg ![]() oraz miara probabilistyczna
oraz miara probabilistyczna ![]() taka, że
taka, że ![]() . Zatem, korzystając z (i),
. Zatem, korzystając z (i), ![]() , czyli
, czyli ![]() . Sprzeczność z (*) kończy dowód.
. Sprzeczność z (*) kończy dowód.
Na zakończenie zaprezentujemy twierdzenie o odwróceniu, pozwalające odczytać gęstość rozkładu za pomocą jego funkcji charakterystycznej. Analogiczny fakt dla zmiennych dyskretnych jest treścią zadania 10 poniżej.
Twierdzenie 2.5
Załóżmy, że ![]() jest rozkładem prawdopodobieństwa w
jest rozkładem prawdopodobieństwa w ![]() o funkcji charakterystycznej
o funkcji charakterystycznej ![]() . Wówczas jeśli
. Wówczas jeśli ![]() , to
, to ![]() ma ciągłą ograniczoną gęstość
ma ciągłą ograniczoną gęstość ![]() daną wzorem
daną wzorem
Dowód:
Rozważmy funkcję
gdzie w trzecim przejściu skorzystaliśmy z twierdzenia Fubiniego (dzięki czynnikowi ![]() wyrażenie podcałkowe jest całkowalne), a w czwartym użyliśmy faktu, iż wewnętrzna całka to funkcja charakterystyczna rozkładu
wyrażenie podcałkowe jest całkowalne), a w czwartym użyliśmy faktu, iż wewnętrzna całka to funkcja charakterystyczna rozkładu ![]() w punkcie
w punkcie ![]() . Jak widać, ostatnie wyrażenie to splot rozkładu
. Jak widać, ostatnie wyrażenie to splot rozkładu ![]() z rozkładem
z rozkładem ![]() , w punkcie
, w punkcie ![]() ; innymi słowy, jeśli
; innymi słowy, jeśli ![]() ,
, ![]() są niezależnymi zmiennymi o rozkładach
są niezależnymi zmiennymi o rozkładach ![]() i
i ![]() , odpowiednio, to
, odpowiednio, to ![]() ma rozkład z gęstością
ma rozkład z gęstością ![]() . Na mocy całkowalności funkcji charakterystycznej
i twierdzenia Lebesgue'a, mamy
. Na mocy całkowalności funkcji charakterystycznej
i twierdzenia Lebesgue'a, mamy ![]() dla każdego
dla każdego ![]() . Wykażemy teraz, że
. Wykażemy teraz, że ![]() . Oczywiście, na mocy lematu Fatou,
. Oczywiście, na mocy lematu Fatou, ![]() . By udowodnić nierówność przeciwną, weźmy
. By udowodnić nierówność przeciwną, weźmy ![]() oraz taką liczbę
oraz taką liczbę ![]() , by
, by ![]() . Ponieważ
. Ponieważ ![]() , to
, to
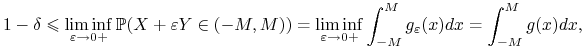 |
i
z dowolności ![]() dostajemy, iż
dostajemy, iż ![]() jest gęstością. Wystarczy teraz skorzystać z zadania 7 z pierwszego rozdziału: punktowa zbieżność
jest gęstością. Wystarczy teraz skorzystać z zadania 7 z pierwszego rozdziału: punktowa zbieżność ![]() pociąga za sobą, iż
pociąga za sobą, iż ![]() zbiega, przy
zbiega, przy ![]() , do rozkładu o gęstości
, do rozkładu o gęstości ![]() ; stąd teza.
; stąd teza.
2.4. Zadania
1. Rozstrzygnąć, czy podane niżej funkcje są funkcjami charakterystycznymi i jeśli tak, podać odpowiedni rozkład.
2. Niech ![]() ,
, ![]() ,
, ![]() ,
, ![]() będą
funkcjami charakterystycznymi pewnych rozkładów. Udowodnić, iż
dowolna kombinacja wypukła tych funkcji jest funkcją
charakterystyczną pewnego rozkładu.
będą
funkcjami charakterystycznymi pewnych rozkładów. Udowodnić, iż
dowolna kombinacja wypukła tych funkcji jest funkcją
charakterystyczną pewnego rozkładu.
3. Dany jest ciąg ![]() niezależnych zmiennych losowych o tym
samym rozkładzie. Zmienna losowa
niezależnych zmiennych losowych o tym
samym rozkładzie. Zmienna losowa ![]() jest od nich niezależna i
ma rozkład Poissona z parametrem
jest od nich niezależna i
ma rozkład Poissona z parametrem ![]() . Wyznaczyć funkcję
charakterystyczną zmiennej
. Wyznaczyć funkcję
charakterystyczną zmiennej ![]() .
.
4. Niech ![]() będzie funkcją charakterystyczną pewnego
rozkładu. Rostrzygnąć, czy
będzie funkcją charakterystyczną pewnego
rozkładu. Rostrzygnąć, czy
są funkcjami charakterystycznymi.
5. Zmienne ![]() są niezależne, przy czym
są niezależne, przy czym ![]() oraz
oraz ![]() mają rozkłady normalne. Udowodnić, że
mają rozkłady normalne. Udowodnić, że ![]() ma rozkład normalny lub
jest stała p.n..
ma rozkład normalny lub
jest stała p.n..
6. Zmienne losowe ![]() są niezależne, przy czym
są niezależne, przy czym ![]() ma
rozkład jednostajny
ma
rozkład jednostajny ![]() , a
, a ![]() ma rozkład zadany przez
ma rozkład zadany przez
Wyznaczyć rozkład zmiennej ![]() .
.
7. Zmienne losowe ![]() są niezależne i
mają ten sam rozkład,
przy czym zmienna
są niezależne i
mają ten sam rozkład,
przy czym zmienna ![]() ma rozkład normalny
ma rozkład normalny
![]() . Wyznaczyć rozkład zmiennych
. Wyznaczyć rozkład zmiennych ![]() .
.
8. Zmienna losowa ![]() ma rozkład jednostajny
ma rozkład jednostajny ![]() . Czy
istnieje niezależna od niej zmienna
. Czy
istnieje niezależna od niej zmienna ![]() taka, że rozkłady zmiennych
taka, że rozkłady zmiennych
![]() oraz
oraz ![]() są takie same?
są takie same?
9. Funkcja charakterystyczna zmiennej losowej ![]() ma drugą
pochodną w zerze. Udowodnić, że
ma drugą
pochodną w zerze. Udowodnić, że ![]() .
.
10. Zmienna losowa ![]() przyjmuje wartości całkowite. Udowodnić, że
przyjmuje wartości całkowite. Udowodnić, że
11. Udowodnić, że dla ![]() funkcja
funkcja ![]() nie jest funkcją charakterystyczną żadnego rozkładu.
nie jest funkcją charakterystyczną żadnego rozkładu.
12. Udowodnić, że ![]() jest funkcją charakterystyczną rozkładu Cauchy'ego w
jest funkcją charakterystyczną rozkładu Cauchy'ego w ![]() , tzn. rozkładu o gęstości
, tzn. rozkładu o gęstości
13. Niech ![]() ,
, ![]() ,
, ![]() będą niezależnymi zmiennymi losowymi o rozkładzie jednostajnym na przedziale
będą niezależnymi zmiennymi losowymi o rozkładzie jednostajnym na przedziale ![]() . Zdefiniujmy
. Zdefiniujmy
gdzie ![]() jest ustalone. Udowodnić, że ciąg
jest ustalone. Udowodnić, że ciąg
jest zbieżny według rozkładu i wyznaczyć funkcję charakterystyczną rozkładu granicznego.
14. Udowodnić, że jeśli ![]() (
(![]() ) są rozkładami Gaussa w
) są rozkładami Gaussa w ![]() i
i ![]() , to
, to ![]() jest rozkładem Gaussa.
jest rozkładem Gaussa.
15. Rzucamy monetą, dla której prawdopodobieństwo wypadnięcia orła wynosi ![]() , aż do momentu, gdy uzyskamy
, aż do momentu, gdy uzyskamy ![]() orłów (łącznie, niekoniecznie pod rząd). Niech
orłów (łącznie, niekoniecznie pod rząd). Niech ![]() oznacza liczbę rzutów. Udowodnić, że
oznacza liczbę rzutów. Udowodnić, że ![]() jest zbieżny według rozkładu gdy
jest zbieżny według rozkładu gdy ![]() .
.
16. Niech ![]() będzie zmienną losową o funkcji
charakterystycznej
będzie zmienną losową o funkcji
charakterystycznej ![]() . Udowodnić, że następujące warunki są
równoważne.
. Udowodnić, że następujące warunki są
równoważne.
(i) Istnieje ![]() takie, że
takie, że ![]() .
.
(ii) Istnieją ![]() takie, że zmienna
takie, że zmienna ![]() jest skoncentrowana
na zbiorze
jest skoncentrowana
na zbiorze ![]() .
.
17. Dany jest ciąg ![]() niezależnych zmiennych losowych o tym samym rozkładzie, zadanym przez
niezależnych zmiennych losowych o tym samym rozkładzie, zadanym przez ![]() . Wykazać, że szereg
. Wykazać, że szereg ![]() jest zbieżny p.n. i wyznaczyć rozkład sumy tego szeregu.
jest zbieżny p.n. i wyznaczyć rozkład sumy tego szeregu.
18. Dla ![]() , niech
, niech
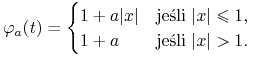 |
Dla jakich wartości parametru ![]() funkcja
funkcja ![]() jest funkcją charakterystyczną rozkładu pewnej zmiennej losowej?
jest funkcją charakterystyczną rozkładu pewnej zmiennej losowej?
19. Załóżmy, że ![]() jest rozkładem prawdopodobieństwa o funkcji charakterystycznej
jest rozkładem prawdopodobieństwa o funkcji charakterystycznej ![]() . Udowodnić, że dla dowolnego
. Udowodnić, że dla dowolnego ![]() zachodzi nierówność
zachodzi nierówność
![\mu([-r,r])\geq 1-\frac{r}{2}\int^{{2/r}}_{{-2/r}}(1-\varphi(s))\mbox{d}s](wyklady/rp2/mi/mi502.png) |
oraz
![\mu([0,r])\leq r\int _{{-\pi/2r}}^{{\pi/2r}}|\varphi(s)|\mbox{d}s.](wyklady/rp2/mi/mi437.png) |




