Zagadnienia
1. Wprowadzenie
1.1. Od autora
Jest kilka ważnych powodów, dla których warto się zająć symulacjami stochastycznymi:
-
Symulacje stochastyczne są prostym sposobem badania zjawisk losowych.
-
Ściśle związane z symulacjami stochastycznymi są metody obliczeniowe nazywane ,,Monte Carlo” (MC). Polegają one na wykorzystaniu ,,sztucznie generowanej” losowości w celu rozwiązania zadań deterministycznych. Metody MC są proste i skuteczne. Dla pewnych problemów MC jest jedynym dostępnym narzędziem obliczeniowym. Dla innych problemów MC jest co prawda mniej efektywne od metod numerycznych, ale za to dużo łatwiejsze!
-
W moim przekonaniu symulacje stochastyczne są wspaniałą pomocą przy nauce rachunku prawdopodobieństwa. Pozwalają lepiej ,,zrozumieć losowość”.
-
Symulacje stochastyczne są dostępne dla każdego. W szczególności, ,,otoczenie” R, które stanowi naprawdę potężne narzędzie, jest rozpowszechniane za darmo!
Jest wreszcie powód najważniejszy:
-
Symulacje stochastyczne są świetną zabawą!
Literatura na temat symulacji stochastycznych jest bardzo obszerna. Godna polecenia jest książka Zielińskiego i Wieczorkowskiego [23], poświęcona w całości generatorom zmiennych losowych. Przedstawia ona bardziej szczegółowo zagadnienia, odpowiadające Rozdziałom 2–4 niniejszego skryptu i zawiera materiał, który zdecydowałem się pominąć: wytwarzanie ,,liczb losowych” o rozkładzie jednostajnym i testowanie generatorów. Podobne zagadnienia są przedstawione trochę w innym stylu w monografii Ripleya [18], która również zawiera wstęp do metod Monte Carlo. Zaawansowane wykłady można znależć w nowoczesnych monografiach Asmussena i Glynna [2], Liu [15], Roberta i Caselli [19]. Pierwsza z nich jest zorientowana bardziej na wyniki teoretyczne, zaś druga bardziej na zastosowania. Świetnym wstępem do metod MCMC są prace Geyera [7] i [8]. Teoria łańcuchów Markowa z uwzględnieniem zagadnień istotnych dla MCMC jest przystępnie przedstawiona w książce Brémaud [4]. Podstawy teoretycznej analizy zrandomizowanych algorytmów (tematy poruszane w Rozdziale 15 skryptu) są znakomicie przedstawione w pracach Jerruma i Sinclaira [11] oraz Jerruma [12].
1.2. Przykłady
Zacznę od kilku przykładów zadań obliczeniowych, które można rozwiązywać symulując losowość. Wybrałem przykłady najprostsze, do zrozumienia których wystarcza zdrowy rozsądek i nie potrzeba wielkiej wiedzy.
Przykład 1.1 (Igła Buffona, 1777)
Podłoga jest nieskończoną płaszczyzną, podzieloną równoległymi
prostymi na ,,deski” szerokości ![]() . Rzucamy ,,losowo” igłę o
długości
. Rzucamy ,,losowo” igłę o
długości ![]() . Elementarne rozważania prowadzą do wniosku, że
. Elementarne rozważania prowadzą do wniosku, że
Buffon zauważył, że tę prostą obserwację można wykorzystać do…obliczania liczby ![]() metodą ,,statystyczną”. Powtórzmy nasze
doświadczenie niezależnie
metodą ,,statystyczną”. Powtórzmy nasze
doświadczenie niezależnie ![]() razy. Oczywiście, mamy do czynienia
ze schematem Bernoulliego, w którym ,,sukcesem” jest przecięcie
prostej. Niech
razy. Oczywiście, mamy do czynienia
ze schematem Bernoulliego, w którym ,,sukcesem” jest przecięcie
prostej. Niech
Wielkość ![]() jest empirycznym odpowiednikiem prawdopodobieństwa
jest empirycznym odpowiednikiem prawdopodobieństwa
![]() i powinna przybliżać to prawdopodobieństwo, przynajmniej dla
dużych
i powinna przybliżać to prawdopodobieństwo, przynajmniej dla
dużych ![]() . W takim razie, możemy za przybliżenie liczby
. W takim razie, możemy za przybliżenie liczby ![]() przyjąć
przyjąć
Statystyk powiedziałby, że zmienna losowa ![]() jest
estymatorem liczby
jest
estymatorem liczby ![]() . To wszystko jest bardzo proste, ale
parę kwestii wymaga uściślenia. Jak duża ma być liczba powtórzeń,
żeby przybliżenie było odpowiednio dokładne? Ale
przecież mamy do czynienia ze ,,ślepym losem”!
Czyż pech nie może sprawić, że mimo dużej liczby doświadczeń przybliżenie jest kiepskie? Czy
odpowiednio dobierając
. To wszystko jest bardzo proste, ale
parę kwestii wymaga uściślenia. Jak duża ma być liczba powtórzeń,
żeby przybliżenie było odpowiednio dokładne? Ale
przecież mamy do czynienia ze ,,ślepym losem”!
Czyż pech nie może sprawić, że mimo dużej liczby doświadczeń przybliżenie jest kiepskie? Czy
odpowiednio dobierając ![]() i
i ![]() możemy poprawić dokładność? A
może da się zaprojektować lepsze doświadczenie?
możemy poprawić dokładność? A
może da się zaprojektować lepsze doświadczenie?
Przykład 1.2 (Sieć zawodnych połączeń)
Niech ![]() będzie grafem skierowanym spójnym. Krawędzie
reprezentują ,,połączenia” pomiędzy wierzchołkami. Krawędź
będzie grafem skierowanym spójnym. Krawędzie
reprezentują ,,połączenia” pomiędzy wierzchołkami. Krawędź
![]() , niezależnie od pozostałych, ulega awarii ze znanym
prawdopodobieństwem
, niezależnie od pozostałych, ulega awarii ze znanym
prawdopodobieństwem ![]() . W rezultacie powstaje losowy podzbiór
. W rezultacie powstaje losowy podzbiór
![]() sprawnych połączeń o rozkładzie prawdopodobieństwa
sprawnych połączeń o rozkładzie prawdopodobieństwa
Jest jasne, jak można symulować to zjawisko: dla każdej krawędzi
![]() ,,losujemy” zmienną
,,losujemy” zmienną ![]() o rozkładzie równomiernym na
o rozkładzie równomiernym na
![]() i przyjmujemy
i przyjmujemy
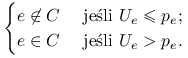 |
Powiedzmy, że interesuje nas możliwość znalezienia ścieżki (ciągu
krawędzi) wiodącej z ustalonego wierzchołka ![]() do innego
wierzchołka
do innego
wierzchołka ![]() . Niech
. Niech
Generujemy niezależnie ![]() kopii
kopii ![]() zbioru
zbioru ![]() .
Nieznane prawdopodobieństwo
.
Nieznane prawdopodobieństwo ![]() przybliżamy
przez odpowiednik próbkowy:
przybliżamy
przez odpowiednik próbkowy:
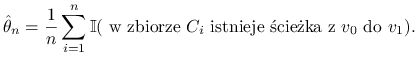 |
Przykład 1.3 (Skomplikowana całka)
Załóżmy, że ![]() są
niezależnymi zmiennymi losowymi o jednakowym rozkładzie
są
niezależnymi zmiennymi losowymi o jednakowym rozkładzie ![]() . Niech
. Niech
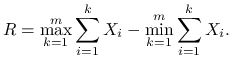 |
Chcemy obliczyć dystrybuantę zmiennej losowej ![]() ,
,
Zauważmy, że z definicji,
![H(x)={\int\cdots\int}_{{\Omega _{m}}}(2\pi)^{{-m/2}}\exp\left[-\frac{1}{2}\sum _{{i=1}}^{m}x_{i}^{2}\right]{\rm d}x_{1}\cdots{\rm d}x_{m},](wyklady/sst/mi/mi105.png) |
gdzie ![]() .
W zasadzie, jest to więc zadanie obliczenia całki. Jednak skomplikowany kształt wielowymiarowego zbioru
.
W zasadzie, jest to więc zadanie obliczenia całki. Jednak skomplikowany kształt wielowymiarowego zbioru ![]() powoduje, że zastosowanie standardowych metod numerycznych jest utrudnione. Z kolei symulowanie zmiennej losowej
powoduje, że zastosowanie standardowych metod numerycznych jest utrudnione. Z kolei symulowanie zmiennej losowej
![]() jest bardzo łatwe, wprost z definicji. Można wygenerować wiele niezależnych zmiennych
jest bardzo łatwe, wprost z definicji. Można wygenerować wiele niezależnych zmiennych ![]() o rozkładzie
takim samym jak
o rozkładzie
takim samym jak ![]() . Wystarczy teraz policzyć ile spośród tych zmiennych jest
. Wystarczy teraz policzyć ile spośród tych zmiennych jest ![]() :
:
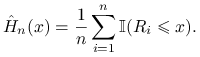 |
Schemat symulacyjnego obliczania prawdopodobieństwa jest taki sam jak w dwu poprzednich przykładach. Podobnie zresztą jak w tamtych przykładach, podstawowy algorytm można znacznie ulepszać, ale dyskusję na ten temat odłóżmy na póżniej.
Przykład 1.4 (Funkcja harmoniczna)
Następujące zadanie jest dyskretnym odpowiednikiem
sławnego zagadnienia Dirichleta.
Niech ![]() będzie podzbiorem kraty całkowitoliczbowej
będzie podzbiorem kraty całkowitoliczbowej ![]() . Oznaczmy przez
. Oznaczmy przez
![]() brzeg tego zbioru, zdefiniowany następująco:
brzeg tego zbioru, zdefiniowany następująco:
Powiemy, że ![]() jest funkcją harmoniczną, jeśli
dla każdego punktu
jest funkcją harmoniczną, jeśli
dla każdego punktu ![]() ,
,
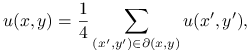 |
gdzie sumowanie rozciąga się na 4 punkty ![]() sąsiadujące z
sąsiadujące z
![]() , to znaczy
, to znaczy ![]() .
.
Mamy daną funkcję na brzegu: ![]() . Zadanie polega na skonstruowaniu jej rozszerzenia harmonicznego, to znaczy takiej funkcji harmonicznej
. Zadanie polega na skonstruowaniu jej rozszerzenia harmonicznego, to znaczy takiej funkcji harmonicznej ![]() , że
, że
![]() dla
dla ![]() .
.
Wyobraźmy sobie błądzenie losowe po kracie,
startujące w punkcie ![]() . Formalnie jest to ciąg losowych punktów określonych następująco:
. Formalnie jest to ciąg losowych punktów określonych następująco:
gdzie ![]() są niezależnymi wektorami losowymi o jednakowym rozkładzie prawdopodobieństwa:
są niezależnymi wektorami losowymi o jednakowym rozkładzie prawdopodobieństwa:
Błądzimy tak długo, aż natrafimy na brzeg obszaru. Formalnie, określamy moment zatrzymania
![]() . Łatwo zauważyć, że funkcja
. Łatwo zauważyć, że funkcja
jest rozwiązaniem zagadnienia! Istotnie, ze wzoru na prawdopodobieństwo całkowite wynika, że
![u(x,y)=\frac{1}{4}\sum _{{(x^{\prime},y^{\prime})\in\partial(x,y)}}\mathbb{E}[\bar{u}(X_{T},Y_{T})|(X_{1},Y_{1})=(x^{\prime},y^{\prime})].](wyklady/sst/mi/mi76.png) |
Wystarczy teraz spostrzeżenie, że rozkład zmiennej losowej
![]() pod warunkiem
pod warunkiem ![]() jest taki sam jak pod warunkiem
jest taki sam jak pod warunkiem ![]() , bo błądzenie ,,rozpoczyna
się na nowo”.
, bo błądzenie ,,rozpoczyna
się na nowo”.
Algorytm Monte Carlo obliczania ![]() oparty na powyższym spostrzeżeniu został wynaleziony przez von Neumanna
i wygląda następująco:
oparty na powyższym spostrzeżeniu został wynaleziony przez von Neumanna
i wygląda następująco:
-
Powtórz wielokrotnie, powiedzmy
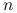 razy, niezależnie doświadczenie:
razy, niezależnie doświadczenie: -
,,błądź startując startując z
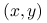 aż do brzegu;
oblicz
aż do brzegu;
oblicz 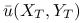 ”
” -
Uśrednij wyniki
 doświadczeń.
doświadczeń.
Dla bardziej formalnego zapisu algorytmu będę się posługiwał pseudo-kodem, który wydaje się zrozumiały bez dodatkowych objaśnień:
| { 'Gen' oznacza 'Generuj' } |
| for |
| begin |
| |
| while |
| begin |
| Gen |
| |
| end |
| |
| end |
Przykład 1.5 (Problem ,,plecakowy”)
Załóżmy, że ![]() jest wektorem o współrzędnych naturalnych
(
jest wektorem o współrzędnych naturalnych
(![]() ) i
) i ![]() . Rozważamy wektory
. Rozważamy wektory ![]() o współrzędnych
zero-jedynkowych (
o współrzędnych
zero-jedynkowych (![]() ). Interesuje nas liczba rozwiązań nierówności
). Interesuje nas liczba rozwiązań nierówności
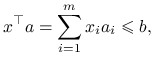 |
a więc liczność ![]() zbioru
zbioru ![]() .
Czytelnik domyśla się z pewnością, skąd nazwa problemu. Dokładne obliczenie liczby rozwiązań jest trudne. Można
spróbować zastosować prostą metodę Monte Carlo. Jeśli zmienna losowa
.
Czytelnik domyśla się z pewnością, skąd nazwa problemu. Dokładne obliczenie liczby rozwiązań jest trudne. Można
spróbować zastosować prostą metodę Monte Carlo. Jeśli zmienna losowa ![]() ma rozkład jednostajny na przestrzeni
ma rozkład jednostajny na przestrzeni ![]() ,
to
,
to ![]() . Wystarczy zatem oszacować to prawdopodobieństwo tak jak w trzech pierwszych przykładach w tym rozdziale.
Generowanie zmiennej losowej o rozkłdzie jednostajnym na przestrzeni
. Wystarczy zatem oszacować to prawdopodobieństwo tak jak w trzech pierwszych przykładach w tym rozdziale.
Generowanie zmiennej losowej o rozkłdzie jednostajnym na przestrzeni ![]() sprowadza się do przeprowadzenia
sprowadza się do przeprowadzenia
![]() rzutów monetą i jest dziecinnie proste. Na czym więc polega problem? Otóż szacowane prawdopodobieństwo może być astronomicznie małe.
Dla, powiedzmy
rzutów monetą i jest dziecinnie proste. Na czym więc polega problem? Otóż szacowane prawdopodobieństwo może być astronomicznie małe.
Dla, powiedzmy ![]() i
i ![]() , to prawdopodobieństwo jest
, to prawdopodobieństwo jest ![]() (proszę się zastanowić jak uzasadnić tę nierówność).
Przeprowadzanie ciągu doświadczeń Bernoulliego z takim prawdopodobieństwem sukcesu jest bardzo nieefektywne – na pierwszy sukces
oczekiwać będziemy średnio
(proszę się zastanowić jak uzasadnić tę nierówność).
Przeprowadzanie ciągu doświadczeń Bernoulliego z takim prawdopodobieństwem sukcesu jest bardzo nieefektywne – na pierwszy sukces
oczekiwać będziemy średnio ![]() , co dla dużych
, co dla dużych ![]() jest po prostu katastrofalne.
jest po prostu katastrofalne.
Metoda, którą naszkicuję należy do rodziny algorytmów MCMC (Monte Carlo opartych na łańcuchach Markowa). Algorytm jest
raczej skomplikowany, ale o ile mi wiadomo jest najefektywniejszym ze znanych sposobów rozwiązania zadania.
Bez straty ogólności możemy przyjąć, że ![]() . Niech
. Niech ![]() oraz
oraz ![]() .
Rozważmy ciąg zadań plecakowych ze zmniejszającą się prawą stroną nierówności, równą kolejno
.
Rozważmy ciąg zadań plecakowych ze zmniejszającą się prawą stroną nierówności, równą kolejno
![]() . Niech więc
. Niech więc ![]() . Zachodzi następujący
,,wzór teleskopowy”:
. Zachodzi następujący
,,wzór teleskopowy”:
Oczywiście, ![]() , a więc możemy uznać, że zadanie sprowadza się do obliczenia ilorazów
, a więc możemy uznać, że zadanie sprowadza się do obliczenia ilorazów ![]() (pomijamy w tym miejscu subtelności związane z dokładnością obliczeń).
Gdybyśmy umieli efektywnie generować zmienne losowe
o rozkładzie jednostajnym na przestrzeni
(pomijamy w tym miejscu subtelności związane z dokładnością obliczeń).
Gdybyśmy umieli efektywnie generować zmienne losowe
o rozkładzie jednostajnym na przestrzeni ![]() , to moglibyśmy postępować w dobrze już znany sposób: liczyć ,,sukcesy” polegające
na wpadnięciu w zbiór
, to moglibyśmy postępować w dobrze już znany sposób: liczyć ,,sukcesy” polegające
na wpadnięciu w zbiór ![]() . Rzecz jasna, możemy losować z rozkładu jednostajnego na kostce
. Rzecz jasna, możemy losować z rozkładu jednostajnego na kostce
![]() i eliminować punkty poza zbiorem
i eliminować punkty poza zbiorem ![]() , ale w ten sposób wpadlibyśmy w pułapkę, od której właśnie uciekamy:
co zrobić jeśli przez sito eliminacji przechodzi jedno na
, ale w ten sposób wpadlibyśmy w pułapkę, od której właśnie uciekamy:
co zrobić jeśli przez sito eliminacji przechodzi jedno na ![]() losowań?
losowań?
Opiszemy pewne wyjście, polegające na zastosowaniu błądzenia losowego po zbiorze ![]() . Dla ustalenia uwagi przyjmijmy
. Dla ustalenia uwagi przyjmijmy
![]() , czyli
, czyli ![]() . Losowy ciąg punktów
. Losowy ciąg punktów ![]() generujemy rekurencyjnie w taki sposób:
generujemy rekurencyjnie w taki sposób:
| for |
| begin |
| |
| Gen |
| |
| if |
| else |
| end |
| end |
Zaczynamy błądzenie w punkcie ![]() . Jeśli w chwili
. Jeśli w chwili ![]() jesteśmy w punkcie
jesteśmy w punkcie ![]() , to próbujemy przejść do
nowego punktu
, to próbujemy przejść do
nowego punktu ![]() , utworzonego przez zmianę jednej, losowo wybranej współrzędnej punktu
, utworzonego przez zmianę jednej, losowo wybranej współrzędnej punktu ![]() (0 zamieniamy na 1 lub z 1 na 0; pozostałe współrzędne zostawiamy bez zmian). Jeśli ,,proponowany punkt
(0 zamieniamy na 1 lub z 1 na 0; pozostałe współrzędne zostawiamy bez zmian). Jeśli ,,proponowany punkt ![]() nie
wypadł” z rozważanej przestrzeni
nie
wypadł” z rozważanej przestrzeni ![]() , to przechodzimy do punktu
, to przechodzimy do punktu ![]() . W przeciwnym wypadku stoimy w punkcie
. W przeciwnym wypadku stoimy w punkcie ![]() .
.
Rzecz jasna, generowane w ten sposób zmienne losowe ![]() nie mają dokładnie rozkładu jednostajnego ani tym bardziej
nie są niezależne. Jednak dla dużych
nie mają dokładnie rozkładu jednostajnego ani tym bardziej
nie są niezależne. Jednak dla dużych ![]() zmienna
zmienna ![]() ma w przybliżeniu rozkład jednostajny:
ma w przybliżeniu rozkład jednostajny:
dla każdego ![]() . Co więcej, z prawdopodobieństwem 1 jest prawdą, że
. Co więcej, z prawdopodobieństwem 1 jest prawdą, że
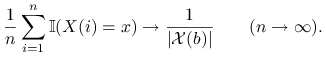 |
Innymi słowy, ciąg ![]() spełnia prawo wielkich liczb – i może być użyty do szacowania liczności podzbiorów przestrzeni
spełnia prawo wielkich liczb – i może być użyty do szacowania liczności podzbiorów przestrzeni ![]() zamiast trudnego do symulowania ciągu niezależnych zmiennych o rozkładzie jednostajnym.
zamiast trudnego do symulowania ciągu niezależnych zmiennych o rozkładzie jednostajnym.




