12. Markowowskie Monte Carlo III. Przykłady zastosowań
12.1. Statystyka bayesowska
Algorytmy MCMC zrewolucjonizowały statystykę bayesowską. Stworzyły możliwość obliczania (w przybliżeniu) rozkładów a posteriori w sytuacji, gdy dokładne, analityczne wyrażenia są niedostępne. W ten sposób statystycy uwolnili się od koniecznośći używania nadmiernie uproszczonych modeli. Zaczęli śmiało budować modele coraz bardziej realistyczne, zwykle o strukturze hierarchicznej. Przedstawię to na jednym dość typowym przykładzie, opartym na pracy [21]. Inne przykłady i doskonały wstęp do tematyki zastosowań MCMC można znaleźć w pracy Geyera [7].
12.1.1. Hierarchiczny model klasyfikacji
Przykład 12.1 (Statystyka małych obszarów)
Zacznijmy od opisania problemu tak zwanych ,,małych obszarów”, który jest dość ważny w dziedzinie badań reprezentacyjnych, czyli w tak zwanej ,,statystyce oficjalnej”. Wyobraźmy sobie, że w celu zbadania kondycji przedsiębiorstw losuje się próbkę, która liczy (powiedzmy) 3500 przedsiębiorstw z całego kraju. Na podstawie tej losowej próbki można dość wiarygodnie szacować (estymować) pewne parametry opisujące populację przedsiębiorstw w kraju. Czy jednak można z rozsądną dokłdnością oszacować sprzedaż w powiecie garwolińskim? W Polsce mamy ponad 350 powiatów. Na jeden powiat przypada średnio 10 przedsiębiorstw wybranych do próbki. Małe obszary to pod-populacje w których rozmiar próbki nie jest wystarczający, aby zastosować ,,zwykłe” estymatory (średnie z próbki). Podejście bayesowskie pozwala ,,pożyczać informację” z innych obszarów. Zakłada się, że z każdym małym obszarem związany jest nieznany parametr, który staramy się estymować. Obserwacje pochodzące z określonego obszaru mają rozkład prawdopodobieństwa zależny od odpowiadającego temu obszarowi parameru. Parametry, zgodnie z filozofią bayesowską, traktuje się jak zmienne losowe. W najprostszej wersji taki model jest zbudowany w następujący sposób.
12.1.1.1. Model bayesowski
-
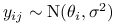 – badana cecha dla
– badana cecha dla 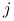 -tej
wylosowanej jednostki
-tej
wylosowanej jednostki 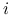 -tego obszaru,
-tego obszaru, 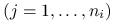 ,
, 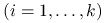 ,
, -
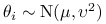 – interesująca nas średnia
w
– interesująca nas średnia
w 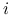 -tym obszarze,
-tym obszarze, -
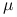 – średnia w całej populacji.
– średnia w całej populacji.
Ciekawe, że ten sam model pojawia się w różnych innych zastosowanianich, na przykład w matematyce ubezpieczeniowej. Przytoczymy klasyczny rezultat dotyczący tego modelu, aby wyjaśnić na czym polega wspomniane ,,pożyczanie informacji”.
12.1.1.2. Estymator bayesowski
W modelu przedstawionym powyżej, łatwo obliczyć estymator bayesowski (przy kwadratowej funkcji straty), czyli wartość oczekiwaną a posteriori. Następujący wzór jest bardzo dobrze znany specjalistom od małych obszarów i aktuariuszom.
Estymator bayesowski dla ![]() -tego obszaru jest średnią ważoną
-tego obszaru jest średnią ważoną ![]() (estymatora opartego na danych
z tego obszaru) i wielkości
(estymatora opartego na danych
z tego obszaru) i wielkości ![]() , która opisuje całą populację, a nie tylko
, która opisuje całą populację, a nie tylko ![]() -ty obszar.
Niestety, proste estymator napisany powyżej zależy od parametrów
-ty obszar.
Niestety, proste estymator napisany powyżej zależy od parametrów ![]() ,
, ![]() i
i ![]() , które w
praktyce są nieznane i które trzeba estymować. Konsekwentnie bayesowskie podejście polega na
traktowaniu również tych parametrów jako zmiennych losowych, czyli nałożeniu na nie rozkłądów a priori.
Powstaje w ten sposób model hierarchiczny.
, które w
praktyce są nieznane i które trzeba estymować. Konsekwentnie bayesowskie podejście polega na
traktowaniu również tych parametrów jako zmiennych losowych, czyli nałożeniu na nie rozkłądów a priori.
Powstaje w ten sposób model hierarchiczny.
12.1.1.3. Hierarchiczny model bayesowski
Uzupełnijmy rozpatrywany powyżej model, dobudowując ,,wyższe piętra” hierarchii. potraktujemy mianowicie
parametry rozkładów a priori: ![]() ,
, ![]() i
i ![]() jako zmienne losowe i wyspecyfikujemy ich rozkłady
a priori.
jako zmienne losowe i wyspecyfikujemy ich rozkłady
a priori.
-
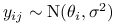 ,
, -
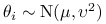 ,
, -
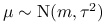 ,
, -
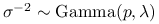 ,
, -
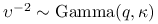 .
.
Zakładamy przy tym, że ![]() ,
, ![]() i
i ![]() są a priori niezależne (niestety, są one zależne a posteriori).
Na szczycie hierarchii mamy ,,hiperparametry”
są a priori niezależne (niestety, są one zależne a posteriori).
Na szczycie hierarchii mamy ,,hiperparametry” ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , o których musimy założyć, ze są znanymi liczbami.
, o których musimy założyć, ze są znanymi liczbami.
Łączny rozkład prawdopodobieństwa wszystkich zmiennych losowych w modelu ma postać
We wzorze powyżej i w dalej traktujemy (trochę nieformalnie) ![]() i
i ![]() jako pojedyncze symbole nowych
zmiennych, żeby nie mnożyć oznaczeń.
Rozkład prawdopodobieństwa a posteriori jest więc taki:
jako pojedyncze symbole nowych
zmiennych, żeby nie mnożyć oznaczeń.
Rozkład prawdopodobieństwa a posteriori jest więc taki:
To jest rozkład ,,docelowy” ![]() , na przestrzeni
, na przestrzeni ![]() , ze nieznaną stałą normującą
, ze nieznaną stałą normującą ![]() .
Choć wygląda na papierze dość prosto, ale obliczenie rozkładów brzegowych, wartości oczekiwanych i innych charakterystyk
jest, łagodnie mówiąc, trudne.
.
Choć wygląda na papierze dość prosto, ale obliczenie rozkładów brzegowych, wartości oczekiwanych i innych charakterystyk
jest, łagodnie mówiąc, trudne.
12.1.2. Próbnik Gibbsa w modelu hierarchicznym
Rozkłady warunkowe poszczególnych współrzędnych są proste i łatwe do generowania. Można te rozkłady ,,odczytać” uważnie patrząc na rozkład łączny:
Dla ustalenia uwagi zajmijmy się rozkładem warunkowym zmiennej ![]() . Kolorem niebieskim oznaczyliśmy
te czynniki łącznej gęstości, które zawierają
. Kolorem niebieskim oznaczyliśmy
te czynniki łącznej gęstości, które zawierają ![]() . Pozostałe, czarne czynniki traktujemy jako stałe.
Stąd widać, jak wygląda rozkład warunkowy
. Pozostałe, czarne czynniki traktujemy jako stałe.
Stąd widać, jak wygląda rozkład warunkowy ![]() ,, przynajmniej z dokładnością do proporcjonalności:
,, przynajmniej z dokładnością do proporcjonalności:
Jest to zatem rozkład ![]() . Zupełnie podobnie rozpoznajemy
inne (pełne) rozkłady warunkowe:
. Zupełnie podobnie rozpoznajemy
inne (pełne) rozkłady warunkowe:
| (12.1) |
gdzie, rzecz jasna, ![]() ,
, ![]() i
i ![]() . Zwróćmy uwagę, że współrzędne
wektora
. Zwróćmy uwagę, że współrzędne
wektora ![]() są warunkowo niezależne (pełny rozkład warunkowy
są warunkowo niezależne (pełny rozkład warunkowy ![]() nie zależy od
nie zależy od ![]() ). Dzięki temy możemy w
próbniku Gibbsa potraktować
). Dzięki temy możemy w
próbniku Gibbsa potraktować ![]() jako cały ,,blok” współrządnych i zmieniać ,,na raz”.
jako cały ,,blok” współrządnych i zmieniać ,,na raz”.
Próbnik Gibbsa ma w tym modelu przestrzeń stanów ![]() składającą się z punktów
składającą się z punktów
![]() . Reguła przejścia próbnika w wersji systematycznej
(duży krok ,,SystemPG”),
. Reguła przejścia próbnika w wersji systematycznej
(duży krok ,,SystemPG”),
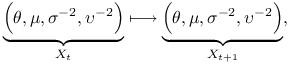 |
jest złożona z następujących ,,małych kroków”:
-
Wylosuj
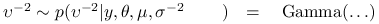 ,
,
-
Wylosuj
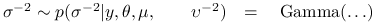 ,
,
-
Wylosuj
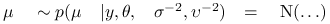 ,
,
-
Wylosuj
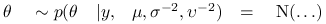 .
.
Łańcuch Markowa jest zbieżny do rozkładu a posteriori:
Najbardziej interesujące są w tym hierarchicznym modelu zmienne ![]() (pozostałe zmienne można uznać za ,,parametry zkłócające).
Dla ustalenia uwagi zajmijmy się zmienną
(pozostałe zmienne można uznać za ,,parametry zkłócające).
Dla ustalenia uwagi zajmijmy się zmienną ![]() (powiedzmy, wartością średnią w pierwszym małym obszarze).
Estymator bayesowski jest to wartość oczekiwana a posteriori tej zmiennej:
(powiedzmy, wartością średnią w pierwszym małym obszarze).
Estymator bayesowski jest to wartość oczekiwana a posteriori tej zmiennej:
Aproksymacją MCMC interesującej nas wielkości są średnie wzdłuż trajektorii łańcucha:
gdzie ![]() dla
dla ![]() .
.
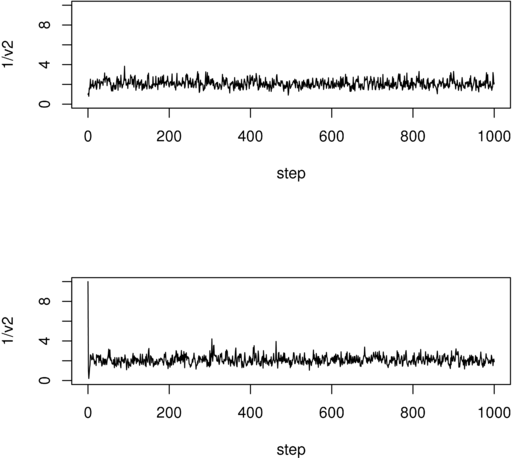
Na Rysunku 12.1 pokazane są dwie przykładowe trajektorie współrzędnej ![]() dla PG poruszającego się
po przestrzeni
dla PG poruszającego się
po przestrzeni ![]() wymiarowej (model uwzględniający 1000 małych obszarów).
Dwie trajektorie odpowiadają dwum różnym punktom startowym. Dla innych zmiennych rysunki wyglądają bardzo podobnie.
Uderzające jest to, jak szybko trajektoria zdaje się ,,osiągać” rozkład stacjonarny, przynajmniej wizualnie.
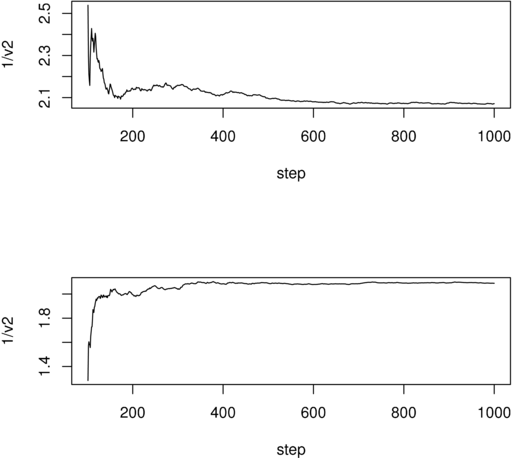
Na Rysunku 12.2 pokazane są kolejne ,,skumulowane” średnie dla tych samych dwóch trajektorii zmiennej
wymiarowej (model uwzględniający 1000 małych obszarów).
Dwie trajektorie odpowiadają dwum różnym punktom startowym. Dla innych zmiennych rysunki wyglądają bardzo podobnie.
Uderzające jest to, jak szybko trajektoria zdaje się ,,osiągać” rozkład stacjonarny, przynajmniej wizualnie.
Na Rysunku 12.2 pokazane są kolejne ,,skumulowane” średnie dla tych samych dwóch trajektorii zmiennej
![]() .
.
12.2. Estymatory największej wiarogodności
Metody MCMC w połączeniu z ideą losowania istotnego (Rozdział 8) znajdują zastosowanie również w statystyce ,,częstościowej”, czyli nie-bayesowskiej. Pokażę przykład, w którym oblicza się meodami Monte carlo estymator największej wiarogodności.
12.2.1. Model auto-logistyczny
Niech ![]() będzie wektorem (konfiguracją) binarnych zmiennych losowych na przestrzeni
będzie wektorem (konfiguracją) binarnych zmiennych losowych na przestrzeni ![]() .
Rozważmy następujący rozkład Gibbsa:
.
Rozważmy następujący rozkład Gibbsa:
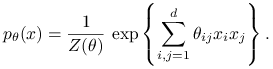 |
Rolę parametru gra macierz ![]() . Zakłąd się, że jest to maciezrz symetryczna .
Stała normująca
. Zakłąd się, że jest to maciezrz symetryczna .
Stała normująca ![]() jest typowo (dla dużych
jest typowo (dla dużych ![]() ) niemożliwa do obliczenia. Stanowi to, jak dalej zobaczymy, poważny problem dla statystyków.
) niemożliwa do obliczenia. Stanowi to, jak dalej zobaczymy, poważny problem dla statystyków.
Przykład 12.2 (Statystyka przestrzenna)
W zastosowaniach ,,przestrzennych” indeks ![]() interpretuje się
jako ,,miejsce”. Zbiór miejsc wyposażony jest w strukturę grafu.
Krawędzie łączą miejsca ,,sąsiadujące”. Piszemy
interpretuje się
jako ,,miejsce”. Zbiór miejsc wyposażony jest w strukturę grafu.
Krawędzie łączą miejsca ,,sąsiadujące”. Piszemy ![]() . Tego typu modele mogą opisywać na przykład
rozprzestrzenianie się chorób lub występowanie pewnych gatunków. Wartośc
. Tego typu modele mogą opisywać na przykład
rozprzestrzenianie się chorób lub występowanie pewnych gatunków. Wartośc ![]() oznacza obecność gatunku
lub występowanie choroby w miejscu
oznacza obecność gatunku
lub występowanie choroby w miejscu ![]() .
Najprostszy model zakłada, że każda zmienna
.
Najprostszy model zakłada, że każda zmienna ![]() zależy tylko od swoich ,,sąsiadów” i to w podobny sposób
w całym rozpatrywanym obszarze. W takim modelu mamy tylko dwa parametry
zależy tylko od swoich ,,sąsiadów” i to w podobny sposób
w całym rozpatrywanym obszarze. W takim modelu mamy tylko dwa parametry ![]() :
:
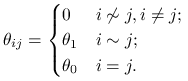 |
Parametr ![]() opisuje ,,skłonność” pojedynczej zmiennej do przyjmowania wartości 1, zaś parametr
opisuje ,,skłonność” pojedynczej zmiennej do przyjmowania wartości 1, zaś parametr ![]() odpowiada za zależność
od zmiennych sąsiadujących (zakaźność choroby, powiedzmy). W typowej dla statystyki przestrzennej sytuacji, rozpatruje się
nawet dziesiątki tysięcy ,,miejsc”. Stała
odpowiada za zależność
od zmiennych sąsiadujących (zakaźność choroby, powiedzmy). W typowej dla statystyki przestrzennej sytuacji, rozpatruje się
nawet dziesiątki tysięcy ,,miejsc”. Stała ![]() jest wtedy sumą niewyobrażalnie wielu (dokładnie
jest wtedy sumą niewyobrażalnie wielu (dokładnie ![]() ) składników.
) składników.
12.2.1.1. Próbnik Gibbsa w modelu auto-logistycznym
,,Pełne” rozkłady warunkowe (full conditionals) są w modelu auto-logistycznym bardzo proste:
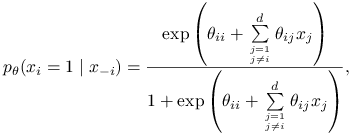 |
gdzie ![]() .
Zatem:
.
Zatem:
-
Symulowanie
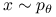 jest łatwe za pomocą próbnika Gibbsa (PG):
jest łatwe za pomocą próbnika Gibbsa (PG): -
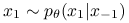 ,
, -
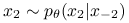 ,
, 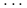
12.2.1.2. Aproksymacja wiarogodności
Estymator największej wiarogodności obliczany metodą Monte Carlo został zaproponowany w pracy Geyer and Thopmpson (1992, JRSS). Rozważmy bardziej ogólną wykładniczą rodzinę rozkładów prawdopodobieństwa:
gdzie ![]() jest wektorem statystyk dostatecznych.
Rozkłady autologistyczne tworzą rodzinę wykładniczą. Wystarczy
jest wektorem statystyk dostatecznych.
Rozkłady autologistyczne tworzą rodzinę wykładniczą. Wystarczy ![]() ustawić w wektor,
statystykami
ustawić w wektor,
statystykami ![]() są
są ![]() i
i ![]() .
Logarytm wiarogodności
.
Logarytm wiarogodności ![]() jest dany pozornie prostym wzorem:
jest dany pozornie prostym wzorem:
Kłopot jest ze stałą normującą ![]() , która w bardziej skomplikowanych modelach jest trudna lub wręcz niemożliwa do
obliczenia. Wspomnieliśmy, że tak właśnie jest dla typowych modeli autologistycznych.
Istnieje jednak prosty sposób aproksymacji stałej
, która w bardziej skomplikowanych modelach jest trudna lub wręcz niemożliwa do
obliczenia. Wspomnieliśmy, że tak właśnie jest dla typowych modeli autologistycznych.
Istnieje jednak prosty sposób aproksymacji stałej ![]() metodą MC. Istotnie, wybierzmy (w zasadzie dowolny)
punkt
metodą MC. Istotnie, wybierzmy (w zasadzie dowolny)
punkt ![]() i zauważmy, że
i zauważmy, że
Pozwala to wyrazić wielkość ![]() jako wartość oczekiwaną względem rozkładu
jako wartość oczekiwaną względem rozkładu ![]() :
:
Powyższe rozważania nie są niczym nowym: to jest po prostu przedstawiony w Rozdziale 8 schemat
losowania istotnego, w specjalnym przypadku rodziny wykładniczej.
Jeśli celem jest maksymalizacja wiarogodności ![]() , to nieznana stała
, to nieznana stała ![]() zupełnie nie przeszkadza
(bo interesującą nas funkcję wiarygodności wystarczy znać z dokładnością do stałej).
zupełnie nie przeszkadza
(bo interesującą nas funkcję wiarygodności wystarczy znać z dokładnością do stałej).
Jeśli umiemy generować zmienne losowe o rozkładzie ![]() , to sposób przybliżonego obliczania
, to sposób przybliżonego obliczania
![]() jest w zasadzie oczywisty.
Generujemy próbkę MC:
jest w zasadzie oczywisty.
Generujemy próbkę MC: ![]() ,
, ![]() gdzie
gdzie
![]() jest w zasadzie dowolne, zaś
jest w zasadzie dowolne, zaś ![]() jest możliwie największe. Obliczamy
jest możliwie największe. Obliczamy
![\hat{Z}(\theta)/Z(\theta _{*})=\frac{1}{n_{*}}\sum _{{k=1}}^{{n_{*}}}\exp\left[(\theta-\theta _{{*}})^{\top}T(x_{*}(k))\right].](wyklady/sst/mi/mi1340.png) |
Aproksymacja logarytmu wiarogodności polega na wstawieniu ![]() w miejsce
w miejsce ![]() we wzorze na
we wzorze na
![]() :
:
![\hat{L}_{{\rm MC}}(\theta)=\theta^{\top}T(x)-\log\underbrace{\sum _{{k=1}}^{{n_{*}}}{\exp[(\theta-\theta _{{*}})^{\top}T(x_{*}(k))}]}_{{\text{ przybliżenie MC }Z(\theta)}}+{\rm const}.](wyklady/sst/mi/mi1358.png) |
Pozostaje wiele szczegółów do dopracowania. Umiemy obliczać wiarogodność jako funkcję ![]() , ale trzeba jeszcze znależć maksimum
tej funkcji. Dobór
, ale trzeba jeszcze znależć maksimum
tej funkcji. Dobór ![]() nie wpływa na poprawność rozumowania ale może mieć zasadniczy wpływ na efektywność algorytmu.
Nie będziemy się w to zagłębiać. Wspomnimy tylko, jak omawiana metoda jest związana z markowowskimi
metodami Monte Carlo, MCMC. Wróćmy do rozkładu auto-logistycznego. Jak losować próbkę z tego rozkładu? Tu przychodzi z pomocą
próbnik Gibbsa. W rzeczy samej, mamy do czynienia z kolejną aproksymacją: PG jest tylko przybliżonym algorytmem
generowania z rozkładu
nie wpływa na poprawność rozumowania ale może mieć zasadniczy wpływ na efektywność algorytmu.
Nie będziemy się w to zagłębiać. Wspomnimy tylko, jak omawiana metoda jest związana z markowowskimi
metodami Monte Carlo, MCMC. Wróćmy do rozkładu auto-logistycznego. Jak losować próbkę z tego rozkładu? Tu przychodzi z pomocą
próbnik Gibbsa. W rzeczy samej, mamy do czynienia z kolejną aproksymacją: PG jest tylko przybliżonym algorytmem
generowania z rozkładu ![]() , które to losowanie pozwala obliczać wiarogodność w przybliżeniu.
Momo wszystko, metody MCMC oferują pewne wyjście lepsze niż bezradne rozłożenie rąk.
, które to losowanie pozwala obliczać wiarogodność w przybliżeniu.
Momo wszystko, metody MCMC oferują pewne wyjście lepsze niż bezradne rozłożenie rąk.