Zagadnienia
15. Markowowskie Monte Carlo VI. Oszacowania dokładności
W tym rozdziale zajmiemy się problemem oszacowania błędu markowowskich algorytmów Monte Carlo. W odróżnieniu od wstępnych rozważań w Rozdziale 10, będą nas interesowały ścisłe nierówności, a nie oceny oparte na twierdzeniach granicznych. Skupimy się na rozkładzie spektralnym macierzy przejścia. Jest to najbardziej znana i zapewne najskuteczniejsza metoda otrzymywania dobrych oszacowań, przynajmniej dla łańcuchów odwracalnych na przestrzeni skończonej.
15.1. Reprezentacja spektralna macierzy odwracalnej
Rozważmy łańcuch nieprzywiedlny i odwracalny z macierzą przejścia ![]() i
rozkładem stacjonarnym
i
rozkładem stacjonarnym ![]() . Zakładamy więc, że dla dowolnych
. Zakładamy więc, że dla dowolnych ![]() spełniona jest zależność
spełniona jest zależność
Niech
![\Pi={\rm diag}(\pi)=\left(\begin{array}[]{cccc}\pi(1)&0&\cdots&0\cr 0&\pi(2)&\cdots&0\cr\vdots&\vdots&\ddots&\vdots\cr 0&0&\cdots&\pi(d)\cr\end{array}\right).](wyklady/sst/mi/mi1822.png) |
Warunek odwracalności możemy zapisać w postaci ![]() .
Wyposażmy przestrzeń
.
Wyposażmy przestrzeń ![]() w iloczyn skalarny
w iloczyn skalarny
gdzie ![]() traktujemy jak wektory kolumnowe. Oczywiście, norma funkcji
traktujemy jak wektory kolumnowe. Oczywiście, norma funkcji ![]() jest zdefiniowana
wzorem
jest zdefiniowana
wzorem ![]() . Macierz
. Macierz ![]() traktujemy jako operator działający z lewej strony na
funkcje, z prawej strony na rozkłady prawdopodobieństwa. Zgodnie z regułami mnożenia macierzy i wektorów, wzory na
traktujemy jako operator działający z lewej strony na
funkcje, z prawej strony na rozkłady prawdopodobieństwa. Zgodnie z regułami mnożenia macierzy i wektorów, wzory na ![]() i
i
![]() są następujące:
są następujące:
Odwracalność ![]() implikuje
implikuje
Znaczy to, że ![]() jest macierzą operatora samosprzężonego względem
iloczynu skalarnego
jest macierzą operatora samosprzężonego względem
iloczynu skalarnego ![]() . W skrócie powiemy, że
. W skrócie powiemy, że ![]() jest
jest
![]() -samosprzężona. Wartości własne
-samosprzężona. Wartości własne ![]() są rzeczywiste i zawarte w przedziale
są rzeczywiste i zawarte w przedziale ![]() .
Uporządkujmy je w kolejności malejącej:
.
Uporządkujmy je w kolejności malejącej:
Wiadomo, że ![]() jest pojedynczą wartością własną. Jeśli
łańcuch jest nieokresowy, to
jest pojedynczą wartością własną. Jeśli
łańcuch jest nieokresowy, to ![]() . Niech
. Niech
Reprezentacja spektralna macierzy ![]() jest następująca:
jest następująca:
gdzie
lub, równoważnie, ![]() . Zauważmy, że kolumny macierzy
. Zauważmy, że kolumny macierzy
są prawostronnymi wektorami własnymi macierzy ![]() tworzącymi bazę
tworzącymi bazę
![]() -ortonormalną. Mamy więc
-ortonormalną. Mamy więc ![]() (oczywiście,
(oczywiście, ![]() jest tu wektorem jedynek) oraz
jest tu wektorem jedynek) oraz
Lewostronne wektory własne ![]() (zapisane wierszowo) są postaci
(zapisane wierszowo) są postaci ![]() :
mamy
:
mamy ![]() . W szczególności,
. W szczególności, ![]() .
Zapiszmy reprezentację spektralną
.
Zapiszmy reprezentację spektralną ![]() w bardziej jawnej formie:
w bardziej jawnej formie:
przy tym
Zauważmy jeszcze, że pierwszy (lub raczej - zerowy) składnik jest macierzą stabilną (o jednakowych wierszach):
Reprezentacja spektralna prowadzi do zgrabnych wyrażeń na potęgi macierzy. Łatwo zauważyć, że
![]() , czyli
, czyli
| (15.1) |
Wiemy, że wszystkie wartości własne ![]() z wyjątkiem zerowej (
z wyjątkiem zerowej (![]() ) oraz, być może, ostatniej
(
) oraz, być może, ostatniej
(![]() ) są co do modułu mniejsze niż 1. Jeżeli więc
) są co do modułu mniejsze niż 1. Jeżeli więc ![]() , to wszystkie
składniki sumy we wzorze (15.1) z wyjątkiem początkowego zmierzają do zera i w rezultacie
, to wszystkie
składniki sumy we wzorze (15.1) z wyjątkiem początkowego zmierzają do zera i w rezultacie
Jest to nic innego jak teza Słabego Twierdzenia Ergodycznego (Twierdzenie 14.5), otrzymana zupełnie inną metodą,
przy założeniu odwracalności. Można pokazać, że warunek ![]() jest równoważny nieokresowości, i jest
konieczny (jeśli
jest równoważny nieokresowości, i jest
konieczny (jeśli ![]() to łańcuch ma okres 2).
to łańcuch ma okres 2).
Następujący lemat będzie podstawą dalszych rozważań i umożliwi ,,przerobienie” STE na jawne wyniki. Zdefiniujmy
Załóżmy, że łańcuch jest nieokresowy, więc ![]() . Pokażemy, że operator
. Pokażemy, że operator ![]() ograniczony do podprzestrzeni
ograniczony do podprzestrzeni
![]() ortogonalnej do
funkcji stałych jest zwężający, ze stałą
ortogonalnej do
funkcji stałych jest zwężający, ze stałą ![]() .
.
Lemat 15.1
Jeżeli ![]() to
to ![]() .
.
Dowód
Wystarczy zauważyć, że
Korzystamy tu z faktu, że ![]() jest samosprzężony, ze wzoru (15.1) i z tego, że
jest samosprzężony, ze wzoru (15.1) i z tego, że ![]() .
.
15.1.1. Oszacowanie szybkości zbieżności
Przejdźmy teraz do jawnych oszacowań szybkości zbieżności w STE.
Wyniki zawarte z tym podrozdziale pochodzą z pracy Diaconisa i Strooka [5].
Dla rozkładu prawdopodobieństwa ![]() definiujemy ,,odległość”
definiujemy ,,odległość” ![]() od rozkładu stacjonarnego
wzorem
od rozkładu stacjonarnego
wzorem
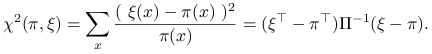 |
Ta ,,odległość” nie ma własności symetrii, więc nie jest metryką, ale to nie przeszkadza. Istotna jest
interpretacja ![]() jako ,,odstępstwa od stacjonarności”. Wykorzystamy
podejście spektralne, w szczególności Lemat 15.1. Niech
jako ,,odstępstwa od stacjonarności”. Wykorzystamy
podejście spektralne, w szczególności Lemat 15.1. Niech ![]() .
.
Stwierdzenie 15.1 (Diaconis i Strook)
Jeśli łańcuch odwracalny, nieprzywiedlny i nieokresowy ma rozkład początkowy ![]() , to
, to
Dowód
Zastosujmy Lemat 15.1 do wektora ![]() który, jak łatwo zauważyć, jest prostopadły do 1.
Otrzymujemy
który, jak łatwo zauważyć, jest prostopadły do 1.
Otrzymujemy
Wniosek 15.1
Dla łańcucha o rozkładzie początkowym skupionym w punkcie ![]() ,
,
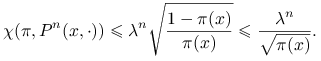 |
Istotnie, mamy jeszcze jedno wyrażenie na ,,odległość” ![]() : dla dowolnego rozkładu
: dla dowolnego rozkładu ![]() ,
,
Wystarczy teraz podstawić ![]() , aby otrzymać
, aby otrzymać ![]() .
.
15.1.2. Oszacowanie normy pełnego wahania
Istnieje prosta nierówność pomiędzy normą pełnego wahania i ,,odległością” ![]() :
:
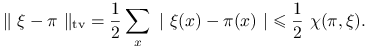 |
Wynika to z następującego rachunku:
Stąd natychmiast otrzymujemy wniosek
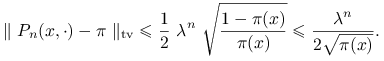 |
15.1.3. Oszacowanie obciążenia estymatora
Rozważmy zadanie obliczania wartości oczekiwanej ![]() dla pewnej funkcji
dla pewnej funkcji ![]() . Niech
. Niech
![]() oznacza ,,scentrowaną” funkcję
oznacza ,,scentrowaną” funkcję ![]() . Natychmiast widać, że
. Natychmiast widać, że ![]() i możemy zastosować
Lemat 15.1. Stąd już tylko mały krok do oszacowania różnicy między
wartością oczekiwaną
i możemy zastosować
Lemat 15.1. Stąd już tylko mały krok do oszacowania różnicy między
wartością oczekiwaną ![]() i wartością stacjonarną
i wartością stacjonarną ![]() .
.
Stwierdzenie 15.2
Jeśli łańcuch jest odwracalny, nieprzywiedlny, nieokresowy i ma rozkład początkowy ![]() , to
, to
gdzie ![]() jest wariancją stacjonarną funkcji
jest wariancją stacjonarną funkcji ![]() .
.
Dowód
Mamy
Rozważmy teraz naturalny estymator
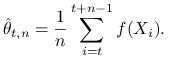 |
Jest to średnia wzdłuż trajektorii łańcucha, dlugości ![]() i ,,opóźniona” o
i ,,opóźniona” o ![]() . Idea jest jasna: ignorujemy początkowy
odcinek trajektorii długości
. Idea jest jasna: ignorujemy początkowy
odcinek trajektorii długości ![]() (tak zwany okres burn-in) aby dać łańcuchowi czas na zbliżenie od rozkładu
stacjonarnego. Później obliczmy średnią. W ten sposób redukujemy obciążenie. Precyzuje to następujący wniosek.
(tak zwany okres burn-in) aby dać łańcuchowi czas na zbliżenie od rozkładu
stacjonarnego. Później obliczmy średnią. W ten sposób redukujemy obciążenie. Precyzuje to następujący wniosek.
Wniosek 15.2
Dla dowolnego ![]() mamy
mamy
Wynika to z nierówności trójkąta i wzoru na sumę szeregu geometrycznego:
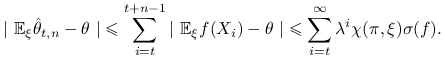 |
Zwróćmy uwagę, że obciążenie maleje w tempie geometrycznym przy ![]() ale zachowuje sią zaledwie jak
ale zachowuje sią zaledwie jak
![]() przy ustalonym
przy ustalonym ![]() i
i ![]() (ponieważ początkowe wyrazy sumy mają na obciążenie wpływ dominujący).
(ponieważ początkowe wyrazy sumy mają na obciążenie wpływ dominujący).
15.2. Oszacowanie błędu średniokwadratowego estymatora
Oszacowanie błędu średniokwadratowego (BŚK) estymatora MCMC jest znaczne trudniejsze i subtelniejsze, niż obciążenia.
15.2.1. Asymptotyczna wariancja
Zacznijmy od wyprowadzenia kolejnego wzoru na asymptotyczną wariancję. Przypomnijmy, że zgodnie ze Stwierdzeniem 14.1,
gdzie
Skorzystajmy z reprezentacji spektralnej macierzy ![]() :
:
![P-{1}\pi^{\top}=\sum _{{i\geq 1}}\lambda _{{i}}v_{{i}}v_{{i}}^{\top}\Pi=V\left(\begin{array}[]{c|ccc}0&&\cdots&0\\
\cline{1-4}&\lambda _{{1}}&\cdots&0\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&\lambda _{{d-1}}\end{array}\right).V^{\top}\Pi](wyklady/sst/mi/mi1745.png) |
Z definicji macierzy ![]() i wzoru (15.1), ponieważ
i wzoru (15.1), ponieważ ![]() , więc
, więc
![A=\sum _{{n=0}}^{{\infty}}(P^{{n}}-{1}\pi^{\top})=V\left(\begin{array}[]{c|ccc}0&&\cdots&0\\
\cline{1-4}&\ddots&\cdots&\\
\vdots&\vdots&{1}/(1-\lambda _{{i}})&\vdots\\
0&&\cdots&\ddots\end{array}\right)V^{\top}\Pi.](wyklady/sst/mi/mi1791.png) |
Wreszcie, ponieważ ![]() , więc
, więc
![\Pi(2A-1+1\pi^{\top})=\Pi V\left(\begin{array}[]{c|ccc}0&&\cdots&0\\
\cline{1-4}&\ddots&\cdots&\\
\vdots&\vdots&(1+\lambda _{i})/(1-\lambda _{i})&\vdots\\
0&&\cdots&\ddots\end{array}\right)V^{\top}\Pi.](wyklady/sst/mi/mi1773.png) |
Zauważmy teraz, że wektor ![]() zawiera współrzędne wektora
zawiera współrzędne wektora ![]() w bazie ON złożonej z prawych wektorów własnych:
w bazie ON złożonej z prawych wektorów własnych:
![]() . Udowodniliśmy w ten sposób następujący fakt.
. Udowodniliśmy w ten sposób następujący fakt.
Stwierdzenie 15.3
Dla łańcucha odwracalnego, wzór na asymptotyczną wariancję przybiera postać
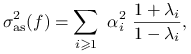 |
gdzie ![]() .
.
Wynika stąd ważna nierówność.
Wniosek 15.3
Dla łańcucha odwracalnego mamy następujące oszacowanie asymptotycznej wariancji:
gdzie ![]() jest największą wartością własną mniejszą od 1, a
jest największą wartością własną mniejszą od 1, a ![]() jest wariancją stacjonarną.
jest wariancją stacjonarną.
Istotnie,
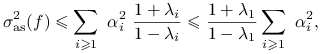 |
a łatwo widzieć, że ![]() . Zwróćmy uwagę, że we Wniosku
15.3 występuje
. Zwróćmy uwagę, że we Wniosku
15.3 występuje ![]() , a nie
, a nie
![]() (największa co do modułu wartość własna mniejsza od 1).
(największa co do modułu wartość własna mniejsza od 1).
Na zakończenie przytoczę jeszcze kilka sugestywnych wzorów.
Uwaga 15.1
Macierz ![]() jest nazywana laplasjanem. Zauważmy, że
jest nazywana laplasjanem. Zauważmy, że
Ponieważ
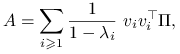 |
uzasadnia to interpretację macierzy ![]() jako ,,uogólnionej odwrotności” laplasjanu.
jako ,,uogólnionej odwrotności” laplasjanu.
Dorzućmy przy okazji jeszcze jedno wyrażenie na asymptotyczną wariancję:
Jeśli ![]() , to
, to ![]() i ostatni wzór możemy przepisać w postaci
i ostatni wzór możemy przepisać w postaci
15.2.2. Oszacowanie BŚK
Wyniki w tym podrozdziale zostały otrzymane przez Aldousa [1].
Pomysł polega na tym, żeby najpierw otrzymać nierówność dla łańcucha stacjonarnego,
a potem postarać się o uogólnienie dla łańcucha o dowolnym rozkładzie początkowym.
Przypomnijmy oznaczenia ![]() ,
, ![]() .
.
Stwierdzenie 15.4 (Aldous, 1987)
Dla dla łańcucha nieprzywiedlnego, odwracalnego i stacjonarnego, ![]() można oszacować w następujący sposób:
można oszacować w następujący sposób:
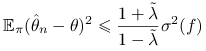 |
gdzie ![]() , zaś
, zaś ![]() jest największą wartością własną mniejszą od
jest największą wartością własną mniejszą od ![]() .
.
Dowód
Korzystamy ze stacjonarności i z rozkładu spektralnego macierzy ![]() .
.
Zwróćmy uwagę na miejsce, w którym pomijamy składniki odpowiadające ujemnym wartościom własnym.
Uzasadnienie jest takie, że dla , ![]() , składniki sumy
, składniki sumy ![]() są
naprzemian ujemne i dodatnie, o malejących wartościach bezwzględnych. Stąd wynika, że
są
naprzemian ujemne i dodatnie, o malejących wartościach bezwzględnych. Stąd wynika, że
![]() i można tę sumę w nierówności opuścić. Jest to ciekawe zjawisko:
ujemne wartości własne pomagają, zmniejszają błąd! Działają podobnie jak zmienne antytetyczne.
i można tę sumę w nierówności opuścić. Jest to ciekawe zjawisko:
ujemne wartości własne pomagają, zmniejszają błąd! Działają podobnie jak zmienne antytetyczne.
Niech teraz ![]() oznacza błąd średniokwadratowy dla łańcucha startującego z punktu
oznacza błąd średniokwadratowy dla łańcucha startującego z punktu ![]() ,
,
Rozpatrzmy łańcuch o rozkładzie początkowym ![]() . Niech
. Niech
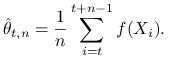 |
będzie średnią długości ![]() obliczany po odrzuceniu
obliczany po odrzuceniu ![]() początkowych zmiennych.
początkowych zmiennych.
Stwierdzenie 15.5
Dla dla łańcucha nieprzywiedlnego, odwracalnego startującego z dowolnego rozkładu ![]() ,
, ![]() można oszacować w następujący sposób:
można oszacować w następujący sposób:
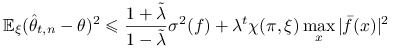 |
gdzie ![]() i
i ![]() .
.
Nierówność podane przez Aldousa w cytowanej pracy była nieco inna.
Stwierdzenie 15.6 (Aldous, 1987)
Dla dla łańcucha nieprzywiedlnego, odwracalnego startującego z dowolnego rozkładu ![]() mamy następujące oszacowanie błędu
mamy następujące oszacowanie błędu ![]() :
:
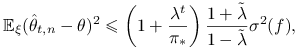 |
gdzie ![]() .
.
Dowód
Istotnie, załóżmy, że łańcuch startuje z deterministycznie wybranego punktu
![]() , czyli
, czyli ![]() . Jeśli otrzymamy oszacowanie niezależne od
. Jeśli otrzymamy oszacowanie niezależne od ![]() , dowód będzie zakończony.
, dowód będzie zakończony.
i zastosujmy Stwierdzenie 15.4. Wykorzystaliśmy tu nierówność ![]() , która wynika z rozkładu
spektralnego:
, która wynika z rozkładu
spektralnego:
W powyższym wzorze symbol ![]() oznacza wektor
oznacza wektor ![]() , gdzie jedynka stoi na
, gdzie jedynka stoi na ![]() -tym miejscu. Skorzystaliśmy
z nierówności Schwarza.
-tym miejscu. Skorzystaliśmy
z nierówności Schwarza.




