Zagadnienia
4. Generowanie zmiennych losowych II. Specjalne metody
4.1. Rozkłady dyskretne
Jak wylosować zmienną losową ![]() o rozkładzie
o rozkładzie ![]() mając dane
mając dane
![]() ? Metoda odwracanie dystrybuanty
w przypadku rozkładów dyskretnych (Przykład 3.6)
przyjmuje następującą postać. Obliczamy
? Metoda odwracanie dystrybuanty
w przypadku rozkładów dyskretnych (Przykład 3.6)
przyjmuje następującą postać. Obliczamy ![]() , gdzie
, gdzie
![]() . Losujemy
. Losujemy ![]() i szukamy przedziału
i szukamy przedziału
![]() w którym leży
w którym leży ![]() .
.
Przykład 4.1 (Algorytm prymitywny)
W zasadzie można to zrobić tak:
| Gen |
| while |
| return |
Problemem jest mała efektywność tego algorytmu. Jedno z możliwych ulepszeń polega na bardziej ,,inteligentnym” lokalizowaniu przedziału
![]() , na przykład metodą bisekcji.
, na przykład metodą bisekcji.
Przykład 4.2 (Algorytm podziału odcinka)
Załóżmy, że mamy rozkład prawdopodobieństwa ![]() na przestrzeni
skończonej i liczby
na przestrzeni
skończonej i liczby ![]() są uporządkowane:
są uporządkowane: ![]() .
.
| Gen |
| repeat |
| |
| if |
| until |
| return |
Przedstawię teraz piękną metodę opartą na innym pomyśle.
Przykład 4.3 (Metoda ,,Alias”)
Przypuśćmy, że mamy dwa ciągi liczb:
![]() , gdzie
, gdzie ![]() oraz
oraz ![]() , gdzie
, gdzie
![]() (to są owe ,,aliasy”). Rozaptrzmy taki algorytm:
(to są owe ,,aliasy”). Rozaptrzmy taki algorytm:
| Gen |
| Gen |
| if |
| return |
Jest jasne, że
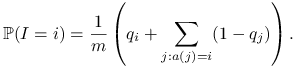 |
Jeśli mamy zadany rozkład prawdopodobieństwa ![]() i chcemy, żeby
i chcemy, żeby
![]() , to musimy dobrać odpowiednio
, to musimy dobrać odpowiednio ![]() i
i ![]() . Można zawsze
tak zrobić, i to na wiele różnych sposobów. Opracowanie algorytmu dobierania wektorów
. Można zawsze
tak zrobić, i to na wiele różnych sposobów. Opracowanie algorytmu dobierania wektorów ![]() i
i ![]() do zadanego
do zadanego ![]() pozostawiamy jako ćwiczenie.
pozostawiamy jako ćwiczenie.
4.2. Schematy kombinatoryczne
4.2.1. Pobieranie próbki bez zwracania
Spośród ![]() obiektów chcemy wybrać losowo
obiektów chcemy wybrać losowo
![]() tak, aby każdy z
tak, aby każdy z ![]() podzbiorów miał jednakowe prawdopodobieństwo.
Oczywiście, można losować tak, jak ze zwracaniem, tylko odrzucać elementy wylosowane powtórnie.
podzbiorów miał jednakowe prawdopodobieństwo.
Oczywiście, można losować tak, jak ze zwracaniem, tylko odrzucać elementy wylosowane powtórnie.
Przykład 4.4 (Losowanie bez zwracania I)
W tablicy ![]() zaznaczamy, które elementy zostały wybrane.
zaznaczamy, które elementy zostały wybrane.
| for |
| repeat |
| repeat |
| Gen |
| until |
| |
| |
| until |
Pewnym ulepszeniem tej prymitywnej metody jest następujący algorytm.
Przykład 4.5 (Losowanie bez zwracania II)
Tablica ![]() ma takie samo znaczenie jak w poprzednim przykładzie. Będziemy teraz
,,przeglądać” elementy
ma takie samo znaczenie jak w poprzednim przykładzie. Będziemy teraz
,,przeglądać” elementy ![]() po kolei, decydując o zaliczeniu do
próbki kolejnego elementu zgodnie z odpowiednim prawdopodobieństwem warunkowym.
Niech
po kolei, decydując o zaliczeniu do
próbki kolejnego elementu zgodnie z odpowiednim prawdopodobieństwem warunkowym.
Niech ![]() oznacza liczbę wybranych, zaś
oznacza liczbę wybranych, zaś ![]() - liczbę przejrzanych poprzednio elementów.
- liczbę przejrzanych poprzednio elementów.
| for |
| repeat |
| Gen |
| if |
| begin |
| |
| |
| end; |
| |
| until |
Przykład 4.6 (Losowanie bez zwracania III)
Tablica ![]() będzie teraz zawierała numery wybieranych elementów. Podobnie jak
poprzednio,
będzie teraz zawierała numery wybieranych elementów. Podobnie jak
poprzednio, ![]() – oznacza liczbę elementów wybranych,
– oznacza liczbę elementów wybranych, ![]() – liczbę przejrzanych.
– liczbę przejrzanych.
| for |
| for |
| begin |
| Gen |
| if |
| begin |
| Gen |
| |
| end |
| end |
Uzasadnienie poprawności tego algorytmu jest
rekurencyjne. Załóżmy, że przed ![]() -tym losowaniem każda próbka
wybrana ze zbioru
-tym losowaniem każda próbka
wybrana ze zbioru ![]() ma prawdopodobieństwo
ma prawdopodobieństwo
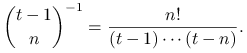 |
W kroku ![]() ta próbka ,,przeżywa” czyli pozostaje bez zmiany z prawdopodobieństwem
ta próbka ,,przeżywa” czyli pozostaje bez zmiany z prawdopodobieństwem
![]() (jest to prawdopodobieństwo, że próbka wylosowana ze zbioru
(jest to prawdopodobieństwo, że próbka wylosowana ze zbioru ![]() nie zawiera elementu
nie zawiera elementu ![]() . Zatem po kroku
. Zatem po kroku ![]() każda próbka nie zawierająca elementu
każda próbka nie zawierająca elementu ![]() ma prawdopodobieństwo
ma prawdopodobieństwo
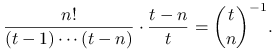 |
Z prawdopodobieństwem ![]() ,,podmieniamy” jeden z elementów próbki (losowo wybrany) na element
,,podmieniamy” jeden z elementów próbki (losowo wybrany) na element ![]() . Sprawdzenie, że każda probka zawierająca element
. Sprawdzenie, że każda probka zawierająca element ![]() ma po
ma po
![]() -tym losowaniu jednakowe prawdopodobieństwo – pozostawiam jako ćwiczenie.
-tym losowaniu jednakowe prawdopodobieństwo – pozostawiam jako ćwiczenie.
4.2.2. Permutacje losowe
Przez permutację losową rozumiemy uporządkowanie ![]() elementów wygenerowane zgodnie z rozkładem jednostajnym na
przestrzeni wszystkich
elementów wygenerowane zgodnie z rozkładem jednostajnym na
przestrzeni wszystkich ![]() możliwych uporządkowań.
Permutację liczb
możliwych uporządkowań.
Permutację liczb ![]() zapiszemy w tablicy
zapiszemy w tablicy ![]() .
Łatwo sprawdzić poprawność następującego algorytmu.
.
Łatwo sprawdzić poprawność następującego algorytmu.
| for |
| for |
| begin |
| Gen |
| |
| end |
4.3. Specjalne metody eliminacji
4.3.1. Iloraz zmiennych równomiernych
Szczególnie często stosowany jest specjalny przypadek metody eliminacji, znany jako algorytm ,,ilorazu zmiennych równomiernych” (Ratio of Uniforms). Zaczniemy od prostego przykładu, który wyjaśni tę nazwę.
Przykład 4.7 (Rozkład Cauchy'ego)
Metodą eliminacji z prostokąta ![]() otrzymujemy zmienną losową
otrzymujemy zmienną losową ![]() o
rozkładzie jednostajnym na półkolu
o
rozkładzie jednostajnym na półkolu ![]() . Kąt
. Kąt ![]() pomiędzy
osią poziomą i punktem
pomiędzy
osią poziomą i punktem ![]() ma, oczywiście, rozkład
ma, oczywiście, rozkład ![]() .
.
| repeat |
| Gen |
| Gen |
| until |
Na wyjściu ![]() , bo
, bo
Ogólny algorytm metody ,,ilorazu równomiernych” oparty jest na następującym fakcie.
Stwierdzenie 4.1
Załóżmy o funkcji ![]() , że
, że
Niech zbiór ![]() będzie określony następująco:
będzie określony następująco:
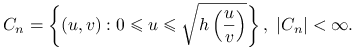 |
Miara Lebesgue'a (pole) tego zbioru jest skończone, ![]() , a zatem można mówić o
rozkładzie jednostajnym
, a zatem można mówić o
rozkładzie jednostajnym ![]() .
.
Jeżeli ![]() i
i ![]() , to
, to ![]() ma gęstość proporcjonalną do
funkcji
ma gęstość proporcjonalną do
funkcji ![]() (
(![]() ).
).
Dowód
,,Pole figury” ![]() jest równe
jest równe
Dokonaliśmy tu zamiany zmiennych:
Jakobian tego przekształcenia jest równy
W podobny sposób,
na mocy znanego wzoru na gęstość przekształconych zmiennych losowych obliczamy
łączną gęstość ![]() :
:
Stąd dostajemy gęstość brzegową ![]() :
:
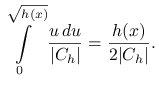 |
Żeby wylosować ![]() stosuje się zazwyczaj eliminację z prostokąta.
Użyteczne jest następujące oszacowanie boków tego prostokąta.
stosuje się zazwyczaj eliminację z prostokąta.
Użyteczne jest następujące oszacowanie boków tego prostokąta.
Stwierdzenie 4.2
Jeśli funkcje ![]() i
i ![]() są ograniczone, wtedy
są ograniczone, wtedy
gdzie
Dowód
Jeśli ![]() to oczywiście
to oczywiście ![]() .
Załóżmy dodatkowo, że
.
Załóżmy dodatkowo, że ![]() i przejdżmy do zmiennych
i przejdżmy do zmiennych ![]() , gdzie
, gdzie ![]() .
Nierówność
.
Nierówność ![]() jest równoważna
jest równoważna ![]() . Ponieważ
. Ponieważ ![]() , więc
dostajemy
, więc
dostajemy ![]() . Dla
. Dla ![]() mamy analogicznie
mamy analogicznie ![]() .
.
Ogólny algorytm RU jest następujący:
| repeat |
| Gen |
| |
| until |
Przykład 4.8 (Rozkład normalny)
Niech
Wtedy
Zauważmy, że ![]() i
i ![]() . Otrzymujemy następujący algorytm:
. Otrzymujemy następujący algorytm:
| repeat |
| Gen |
| |
| |
| until |
4.3.2. Gęstości przedstawione szeregami
Ciekawe, że można skonstruować dokładne algorytmy eliminacji bez konieczności dokładnego obliczania docelowej gęstości ![]() .
Podstawowy pomysł jest następujący. Niech
.
Podstawowy pomysł jest następujący. Niech ![]() , podobnie jak poprzednio, będzie funkcją proporcjonalną do
gęstości (nie jest potrzebna stała normująca) i
, podobnie jak poprzednio, będzie funkcją proporcjonalną do
gęstości (nie jest potrzebna stała normująca) i ![]() . Załóżmy, że mamy dwa ciągi funkcji, przybliżające
. Załóżmy, że mamy dwa ciągi funkcji, przybliżające ![]() z dołu i z góry:
z dołu i z góry:
Jeśli umiemy ewaluować funkcje ![]() i
i ![]() to możemy uruchomić następujący algorytm:
to możemy uruchomić następujący algorytm:
| repeat |
| Gen |
| Gen |
| repeat |
| |
| if |
| begin |
| until |
| until FALSE |
Poniższy algorytm jest znany jako metoda szeregów zbieżnych. Zakładamy, że
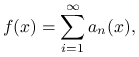 |
przy czym reszty tego szeregu umiemy oszacować z góry przez znane funkcje,
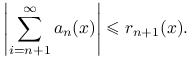 |
Pseudo-kod algorytmu jest taki:
| repeat |
| Gen |
| Gen |
| repeat |
| |
| |
| until |
| until |
| return |
Metoda szeregów naprzemiennych jest dostosowana do sytuacji gdy
![f(x)=g(x)\sum _{{i=0}}^{\infty}(-1)^{n}a_{n}(x)=g(x)\left[1-a_{1}(x)+a_{2}(x)-a_{3}(x)\ldots\right],](wyklady/sst/mi/mi390.png) |
gdzie
![]() .
Wiadomo, że w takiej sytuacji sumy częściowe przybliżają sumę szeregu na przemian z nadmiarem i z niedomiarem.
Ten fakt wykorzystuje algorytm szeregów naprzemiennych:
.
Wiadomo, że w takiej sytuacji sumy częściowe przybliżają sumę szeregu na przemian z nadmiarem i z niedomiarem.
Ten fakt wykorzystuje algorytm szeregów naprzemiennych:
| repeat |
| Gen |
| Gen |
| repeat |
| |
| |
| if |
| |
| |
| until |
| until FALSE |
Przykład 4.9
Rozkład Kołmogorowa-Smirnowa ma dystrybuantę
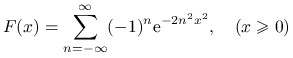 |
i gęstość
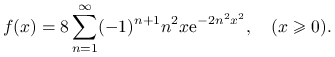 |
Możemy zastosować metodę szeregów naprzemiennych, kładąc
oraz




