Zagadnienia
5. Generowanie zmiennych losowych III. Rozkłady wielowymiarowe
5.1. Ogólne metody
Wiele spośród ogólnych metod generowania zmiennych losowych jest całkowicie niezależnych od wymiaru. W szczególności, metody eliminacji, kompozycji i przekształceń są z powodzeniem stosowane do generowania zmiennych losowych wielowymiarowych. Wyjątek stanowi ,,najbardziej ogólna” metoda odwracania dystrybuanty, która nie ma naturalnego odpowiednika dla wymiaru większego niż 1.
5.1.1. Metoda rozkładów warunkowych
Jest to właściwie jedyna metoda ,,w zasadniczy sposób wielowymiarowa”.
Opiera się na przedstawieniu gęstości łącznej zmiennych losowych
![]() jako iloczynu gęstości brzegowej i gęstości
warunkowych (wzór łańcuchowy):
jako iloczynu gęstości brzegowej i gęstości
warunkowych (wzór łańcuchowy):
Wynika stąd następujący algorytm:
| for |
| Gen |
Przykład 5.1 (Wielowymiarowy rozkład normalny)
Ograniczymy się do zmiennych losowych ![]() pochodzących z rozkładu dwuwymiarowego
pochodzących z rozkładu dwuwymiarowego ![]() o gęstości
o gęstości
![f(x_{1},x_{2})=\frac{1}{2\pi\sigma _{1}\sigma _{2}\sqrt{1-\rho^{2}}}\exp\bigg[-\frac{1}{2(1-\rho^{2})}\Big(\frac{x_{1}^{2}}{\sigma _{1}^{2}}-2\rho\frac{x_{1}x_{2}}{\sigma _{1}\sigma _{2}}+\frac{x_{2}^{2}}{\sigma _{2}^{2}}\Big)\bigg].](wyklady/sst/mi/mi589.png) |
Jak wiadomo (można to sprawdzić elementarnym rachunkiem),
![f(x_{2}|x_{1})=\frac{1}{\sqrt{2\pi}\sigma _{2}\sqrt{1-\rho^{2}}}\exp\bigg[-\frac{1}{2\sigma _{2}^{2}(1-\rho^{2})}\Big(x_{2}-\rho\frac{\sigma _{2}}{\sigma _{1}}x_{1}\Big)^{2}\bigg].](wyklady/sst/mi/mi481.png) |
To znaczy, że ![]() jest rozkładem brzegowym
jest rozkładem brzegowym ![]() oraz
oraz
jest rozkładem warunkowym ![]() dla
dla ![]() . Algorytm jst więc następujący.
. Algorytm jst więc następujący.
| Gen |
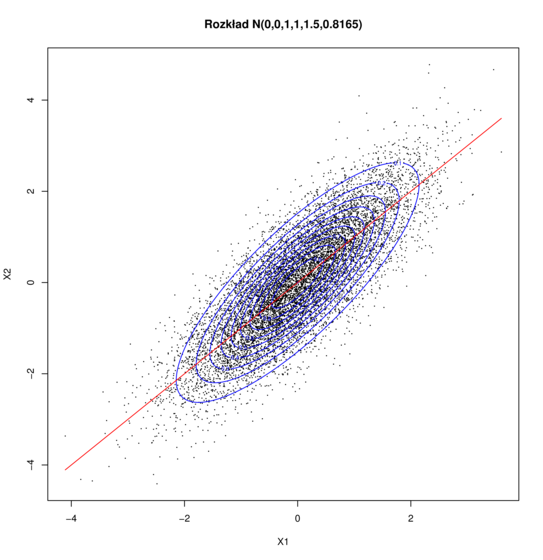
Efekt działania powyższego algorytmu widać na Rysunku 5.1. W tym konkretnym przykładzie
![]() ma rozkład brzegowy
ma rozkład brzegowy ![]() , zaś
, zaś ![]() ma rozkład warunkowy
ma rozkład warunkowy ![]() . Zauważmy, że
. Zauważmy, że
![]() i
i ![]() . Prosta
. Prosta ![]() jest wykresem funkcji regresji
jest wykresem funkcji regresji ![]() i jest przedstawiona na wykresie.
Pokazane są też poziomice gęstości (elipsy). Warto zwrócić uwagę, że funkcja regresji nie pokrywa się
ze wspólną osią tych elips. Dlaczego? Jak obliczyć oś?
i jest przedstawiona na wykresie.
Pokazane są też poziomice gęstości (elipsy). Warto zwrócić uwagę, że funkcja regresji nie pokrywa się
ze wspólną osią tych elips. Dlaczego? Jak obliczyć oś?
Uogólnienie na przypadek rozkładu normalnego
![]() , z niezerowymi średnimi, jest banalne. Uogólnienie na wyższe
wymiary też nie jest skomplikowane. Okazuje się jednak, że metoda rozkładów warunkowych dla rozkładów normalnych prowadzi to do algorytmu identycznego jak otrzymany metodą przekształceń.
, z niezerowymi średnimi, jest banalne. Uogólnienie na wyższe
wymiary też nie jest skomplikowane. Okazuje się jednak, że metoda rozkładów warunkowych dla rozkładów normalnych prowadzi to do algorytmu identycznego jak otrzymany metodą przekształceń.
5.1.2. Metoda przeksztalceń
Podstawą jest następujące twierdzenie o przekształcaniu gęstości.
Twierdzenie 5.1
Załóżmy, że ![]() jest
jest ![]() -wymiarową zmienną losową o wartościach w otwartym
zbiorze
-wymiarową zmienną losową o wartościach w otwartym
zbiorze ![]() . Jeżeli
. Jeżeli
i ![]() jest dyfeomorfizmem, to
jest dyfeomorfizmem, to
Przykład 5.2 (Wielowymiarowy rozkład normalny)
Rozważmy niezależne zmienne losowe ![]() .
Wektor
.
Wektor ![]() ma
ma ![]() -wymiarowy rozkład normalny
-wymiarowy rozkład normalny
![]() o gęstości
o gęstości
Jeżeli teraz R jest nieosobliwą macierzą ![]() to przekształcenie
to przekształcenie
![]() jest dyfeomorfizmem z jakobianem
jest dyfeomorfizmem z jakobianem ![]() . Z Twierdzenia 5.1 wynika, że wektor losowy
. Z Twierdzenia 5.1 wynika, że wektor losowy
![]() ma rozkład normalny o gęstości
ma rozkład normalny o gęstości
gdzie ![]() . Innymi słowy,
. Innymi słowy,
![]() . Algorytm generacji jest oczywisty:
. Algorytm generacji jest oczywisty:
| Gen |
5.2. Kilka ważnych przykładów
Rozmaitych rozkładów wielowymiarowych jest więcej, niż gwiazd na niebie – a wśród nich tyle przykładów ciekawych i ważnych! Musiałem wybrać zaledwie kilka z nich. Rzecz jasna, wybrałem te, które mi się szczególnie podobają.
5.2.1. Rozkłady sferyczne i eliptyczne
Najważniejszy, być może, przykład to wielowymiarowy rozkład normalny, omówiony już w 5.2. Rozpatrzymy teraz rozklady jednostajne na kuli
i sferze
Oczywiście, ![]() oznacza normę euklidesową,
oznacza normę euklidesową,
![]() . Rozkład
. Rozkład ![]() ma po prostu stałą gęstość względem
ma po prostu stałą gęstość względem ![]() -wymiarowej miary Lebesgue'a na kuli.
Rozkład
-wymiarowej miary Lebesgue'a na kuli.
Rozkład ![]() ma stałą gęstość względem
ma stałą gęstość względem ![]() -wymiarowej miary ,,powierzchniowej” na sferze. Oba te rozkłady są niezmiennicze względem
obrotów (liniowych przekształceń ortogonalnych)
-wymiarowej miary ,,powierzchniowej” na sferze. Oba te rozkłady są niezmiennicze względem
obrotów (liniowych przekształceń ortogonalnych) ![]() . Takie rozkłady nazywamy sferycznie symetrycznymi lub krócej:
sferycznymi. Zauważmy, że zmienną losową o rozkładzie
. Takie rozkłady nazywamy sferycznie symetrycznymi lub krócej:
sferycznymi. Zauważmy, że zmienną losową o rozkładzie
![]() możemy interpretować jako losowo wybrany kierunek w
przestrzeni
możemy interpretować jako losowo wybrany kierunek w
przestrzeni ![]() -wymiarowej. Algorytmy ,,poszukiwań losowych” często
wymagają generowania takich losowych kierunków.
-wymiarowej. Algorytmy ,,poszukiwań losowych” często
wymagają generowania takich losowych kierunków.
Rozkłady jednostajne na kuli i sferze są blisko ze sobą związane.
-
Jeśli
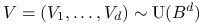 i
i 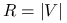 to
to
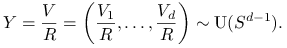
Łatwo też zauważyć, że
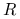 jest zmienną losową o
rozkładzie
jest zmienną losową o
rozkładzie 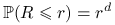 niezależną od
niezależną od 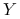 .
. -
Jeśli
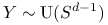 i
i 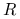 jest niezależną zmienną losową o
rozkładzie
jest niezależną zmienną losową o
rozkładzie 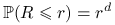 to
to 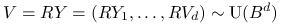 .
.
Zmienną ![]() łatwo wygenerować metodą odwracania dystrybuanty.
łatwo wygenerować metodą odwracania dystrybuanty.
Najprostszy wydaje się algorytm eliminacji:
| repeat |
| Gen |
| until |
W istocie, dokładnie ta metoda, dla ![]() , była częścią algorytmu biegunowego
Marsaglii. Problem w tym, że w wyższych wymiarach
efektywnosc eliminacji gwałtownie maleje. Prawdopodobieństwo akceptacji jest równe
stosunkowi ,,objętości” kuli
, była częścią algorytmu biegunowego
Marsaglii. Problem w tym, że w wyższych wymiarach
efektywnosc eliminacji gwałtownie maleje. Prawdopodobieństwo akceptacji jest równe
stosunkowi ,,objętości” kuli ![]() do kostki
do kostki ![]() . Ze znanego wzoru na objętość kuli
. Ze znanego wzoru na objętość kuli ![]() -wymiarowej wynika, że
-wymiarowej wynika, że
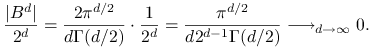 |
Zbieżność do zera jest bardzo szybka. Dla dużego ![]() kula jest znikomą
częścią opisanej na niej kostki.
kula jest znikomą
częścią opisanej na niej kostki.
Inna metoda, którą z powodzeniem stosuje się dla ![]() jest związana
ze współrzędnymi biegunowymi:
jest związana
ze współrzędnymi biegunowymi:
| Gen |
| Gen |
| Gen |
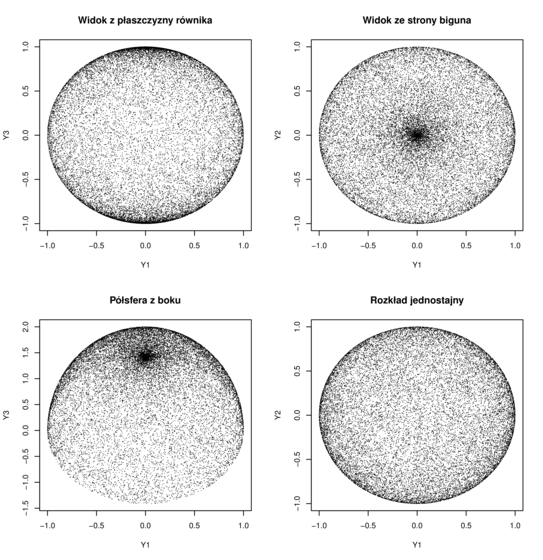
Efekt działania algorytmu ,,współrzędnych sferycznych” jest widoczny na trzech początkowych obrazkach
na Rysunku 5.2.
Górny lewy rysunek przedstawia punkty widoczne ,,z płaszczyzny równika”,
czyli ![]() . Górny prawy – te same punkty widziane ,,znad bieguna”,
czyli
. Górny prawy – te same punkty widziane ,,znad bieguna”,
czyli ![]() . Dolny lewy – górną półsferę widzianą ,,skośnie”,
czyli
. Dolny lewy – górną półsferę widzianą ,,skośnie”,
czyli ![]() , gdzie
, gdzie ![]() . Dla porównania,
na ostatnim rysunku po prawej stronie u dołu – punkty wylosowane
rzeczywiście z rozkładu
. Dla porównania,
na ostatnim rysunku po prawej stronie u dołu – punkty wylosowane
rzeczywiście z rozkładu ![]() przy pomocy poprawnego algorytmu podanego
niżej.
przy pomocy poprawnego algorytmu podanego
niżej.
| Gen |
| Gen |
Przykład 5.3 (Wielowymiarowe rozkłady Studenta)
Niech ![]() będzie wektorem losowym o rozkładzie
będzie wektorem losowym o rozkładzie
![]() , zaś
, zaś ![]() – niezależną zmienną losową o rozkładzie
– niezależną zmienną losową o rozkładzie ![]() .
Wektor
.
Wektor
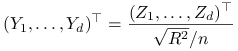 |
ma, z definicji, Sferyczny rozkład ![]() -Studenta z
-Studenta z ![]() stopniami swobody. Gęstość tego rozkładu (z dokładnością do stałej normującej) jest równa
stopniami swobody. Gęstość tego rozkładu (z dokładnością do stałej normującej) jest równa
![f(y)=f(y_{1},\ldots,y_{d})\propto\left[1+\frac{1}{n}\big(\sum y_{i}^{2}\big)\right]^{{-({n+d})/{2}}}=\left[1+\frac{1}{n}|y|^{2}\right]^{{-({n+d})/{2}}}.](wyklady/sst/mi/mi599.png) |
W przypadku jednowymiarowym, a więc przyjmując ![]() , otrzymujemy
dobrze znane rozklady t-Studenta z
, otrzymujemy
dobrze znane rozklady t-Studenta z ![]() stopniami swobody o gęstości
stopniami swobody o gęstości
W szczególnym przypadku, biorąc za liczbę stopni swobody ![]() , otrzymujemy rozkłady Cauchy'ego. Na przykład, dwuwymiarowy rozkład Cauchy'ego ma taką gęstość:
, otrzymujemy rozkłady Cauchy'ego. Na przykład, dwuwymiarowy rozkład Cauchy'ego ma taką gęstość:
Użytecznym uogólnieniem rozkładów sferycznych są rozkłady eliptyczne. Są
one określone w następujący sposób.
Niech ![]() będzie macierzą symetryczną i nieosbliwą.
Nazwijmy uogólnionym obrotem przekształcenie liniowe, które zachowuje uogólnioną normę
będzie macierzą symetryczną i nieosbliwą.
Nazwijmy uogólnionym obrotem przekształcenie liniowe, które zachowuje uogólnioną normę ![]() .
Rozkład jest z definicji eliptycznie konturowany lub krócej eliptyczny, gdy jest niezmienniczy względem uogólnionych obrotów (dla ustalonej macierzy
.
Rozkład jest z definicji eliptycznie konturowany lub krócej eliptyczny, gdy jest niezmienniczy względem uogólnionych obrotów (dla ustalonej macierzy ![]() ).
).
5.2.2. Rozklady Dirichleta
Definicja 5.1
Mówimy, że ![]() -wymiarowa zmienna losowa
-wymiarowa zmienna losowa ![]() ma rozkład Dirichleta,
ma rozkład Dirichleta,
jesli ![]() i zmienne
i zmienne ![]() mają gęstość
mają gęstość
Parametry ![]() mogą być dowolnymi liczbami dodatnimi.
mogą być dowolnymi liczbami dodatnimi.
Uwaga 5.1
Rozkłady Dirichleta dla ![]() są to w istocie rozkłady beta:
są to w istocie rozkłady beta:
Wniosek 5.1
Jeśli ![]() są niezależnymi zmiennymi o jednakowym
rozkładzie jednostajnym
są niezależnymi zmiennymi o jednakowym
rozkładzie jednostajnym ![]() i
i
oznaczają statystyki pozycyjne, to ![]()
maja rozklad ![]() .
.
Twierdzenie 5.2
Jeśli ![]() są niezależnymi zmiennymi losowymi o rozkładach
gamma,
są niezależnymi zmiennymi losowymi o rozkładach
gamma,
i ![]() to
to
Wektor losowy ![]() jest niezależny od
jest niezależny od ![]() .
.
Dowód
Obliczymy łączną gęstość zmiennych losowych ![]() . Ze wzoru na przekształcenie gęstości wynika, że
. Ze wzoru na przekształcenie gęstości wynika, że
ponieważ jakobian przekształcenia odwrotnego jest równy
![]() . Wystarczy teraz zauważyć, że
. Wystarczy teraz zauważyć, że
Wniosek 5.2
Dla niezależnych zmiennych losowych o jednakowym rozkładzie wykładniczym,
jeśli ![]() to
to
Wiele ciekawych własności rozkładów Dirichleta wynika niemal natychmiast z 5.2 (choć nie tak łatwo wyprowadzić je posługując się gęstością 5.2). Mam na myśli przede wszystkim zasadniczą własność ,,grupowania zmiennych”.
Wniosek 5.3
Rozważmy rozbicie zbioru indeksów na sumę rozłącznych podzbiorów:
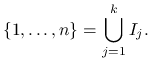 |
Jeżeli ![]() i
rozważymy ,,zgrupowane zmienne”
i
rozważymy ,,zgrupowane zmienne”
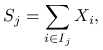 |
to wektor tych zmiennych ma też rozkład Dirichleta,
gdzie
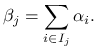 |
Co więcej, każdy z wektorów ![]() ma rozkład Dirichleta
ma rozkład Dirichleta
![]() i wszystkie te wektory są
niezależne od
i wszystkie te wektory są
niezależne od ![]() .
.
Przykład 5.4
Wniosek 5.3 razem z 5.1 pozwala szybko generować wybrane statystyki pozycyjne. Na przykład łączny rozkład dwóch statystyk pozycyjnych z rozkładu jednostajnego jest wyznaczony przez rozkład trzech ,,zgrupowanych spacji”:
Przykład 5.5 (Rozkład dwumianowy)
Aby wygenerować zmienną o rozkładzie dwumianowym ![]() wystarczy rozpoznać między którymi statystykami pozycyjnymi z rozkładu
wystarczy rozpoznać między którymi statystykami pozycyjnymi z rozkładu ![]() leży liczba
leży liczba ![]() . Nie musimy w tym celu
generować wszystkich staystyk pozycyjnych, możemy wybierać
,,najbardziej prawdopodobne”. W połączeniu 5.4 daje to
następujący algorytm.
. Nie musimy w tym celu
generować wszystkich staystyk pozycyjnych, możemy wybierać
,,najbardziej prawdopodobne”. W połączeniu 5.4 daje to
następujący algorytm.
| repeat |
| |
| Gen |
| if |
| begin |
| else |
| begin |
| until |
Metoda generowania zmiennych o rozkładzie Dirichleta opiera sie na następującym fakcie, który jest w istocie szczególnym przypadkiem ,,reguły grupowania” 5.3.
Wniosek 5.4
Jeśli ![]() i, dla
i, dla
![]() , określimy
, określimy ![]() to zmienne
to zmienne
są niezależne i
Odwrotnie, jeśli zmienne ![]() są niezależne i każda z nich
ma rozkład beta, to wektor
są niezależne i każda z nich
ma rozkład beta, to wektor ![]() ma rozkład Dirichleta.
ma rozkład Dirichleta.
Oczywiście, jeśli wygenerujemy niezależne zmienne ![]() o rozkładach beta, to zmienne
o rozkładach beta, to zmienne ![]() łatwo ,,odzyskać” przy
pomocy wzorów:
łatwo ,,odzyskać” przy
pomocy wzorów:
Powyższe równania określają algorytm generowania zmiennych o
rozkładzie ![]() .
.