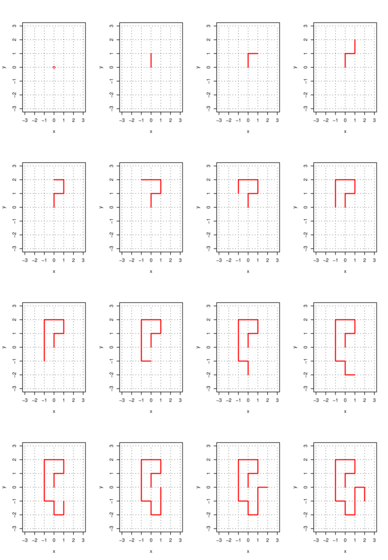8. Algorytmy Monte Carlo I. Obliczanie całek
Duża część zastosowań metod MC wiąże się z obliczaniem całek lub sum. Typowe zadanie polega na obliczeniu wartości oczekiwanej
gdzie ![]() jest zmienną losową o rozkładzie prawdopodobieństwa
jest zmienną losową o rozkładzie prawdopodobieństwa ![]() na przestrzeni
na przestrzeni ![]() , zaś
, zaś
![]() . Zazwyczaj
. Zazwyczaj ![]() jest podzbiorem wielowymiarowej przestrzeni euklidesowej
lub jest zbiorem skończonym ale bardzo licznym (na przykład zbiorem pewnych obiektów kombinatorycznych). Jeśli
jest podzbiorem wielowymiarowej przestrzeni euklidesowej
lub jest zbiorem skończonym ale bardzo licznym (na przykład zbiorem pewnych obiektów kombinatorycznych). Jeśli ![]() i rozkład
i rozkład ![]() jest opisany przez
gęstość
jest opisany przez
gęstość ![]() to całka określająca wartość oczekiwaną jest zwykłą całką Lebesgue'a.
W tym przypadku zatem możemy napisać
to całka określająca wartość oczekiwaną jest zwykłą całką Lebesgue'a.
W tym przypadku zatem możemy napisać
Równie ważny w zastosowaniach jest przypadek dyskretnej przestrzeni ![]() . Jeśli
. Jeśli
![]() , to
, to
W dalszym ciągu tego rozdziału utożsamiamy rozkład ![]() z funkcją
z funkcją ![]() .
Zwróćmy uwagę, że przedstawiamy tu
.
Zwróćmy uwagę, że przedstawiamy tu ![]() jako wartość oczekiwaną tylko dla wygody oznaczeń;
w istocie każda całka, suma, (a także prawdopodobieństwo zdarzenia losowego) jest
wartością oczekiwaną.
jako wartość oczekiwaną tylko dla wygody oznaczeń;
w istocie każda całka, suma, (a także prawdopodobieństwo zdarzenia losowego) jest
wartością oczekiwaną.
Na pierwszy rzut oka nie widać czym polega problem! Sumowanie wykonuje każdy kalkulator, całki się sprawnie oblicza numerycznie. Ale nie zawsze. Metody MC przydają się w sytuacjach gdy spotyka się z następującymi trudnościami (lub przynajmniej którąś z nich).
-
Przestrzeń
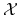 jest ogromna. To znaczy wymiar
jest ogromna. To znaczy wymiar 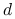 jest bardzo duży lub skończona przestrzeń zawiera astronomicznie dużą liczbę punktów.
jest bardzo duży lub skończona przestrzeń zawiera astronomicznie dużą liczbę punktów. -
Rozkład prawdopodobieństwa
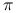 jest ,,skupiony” w małej części ogromnej przestrzeni
jest ,,skupiony” w małej części ogromnej przestrzeni 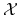 .
. -
Nie ma podstaw do zakładania, że funkcja
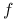 jest w jakimkolwiek sensie ,,gładka”
(co jest warunkiem stosowania standardowych numerycznych metod całkowania).
jest w jakimkolwiek sensie ,,gładka”
(co jest warunkiem stosowania standardowych numerycznych metod całkowania). -
Gęstość
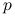 rozkładu
rozkładu 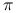 jest znana tylko z dokładnością do stałej normującej. Innymi słowy, umiemy obliczać
jest znana tylko z dokładnością do stałej normującej. Innymi słowy, umiemy obliczać 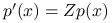 ale nie znamy stałej
ale nie znamy stałej 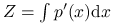 . Czsem zadanie polega właśnie na obliczeni tej stałej (
. Czsem zadanie polega właśnie na obliczeni tej stałej (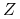 jest nazwane ,,funkcją podziału” lub sumą statystyczną).
jest nazwane ,,funkcją podziału” lub sumą statystyczną).
Prosta metoda MC (po angielsku nazywana bardziej brutalnie: Crude Monte Carlo,
czyli CMC) nasuwa się sama. Należy wygenerować ![]() niezależnych zmiennych losowych
niezależnych zmiennych losowych
![]() o jednakowym rozkładzie
o jednakowym rozkładzie ![]() i za estymator wartości oczekiwanej
wziąć średnią z próbki,
i za estymator wartości oczekiwanej
wziąć średnią z próbki,
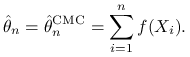 |
Mocne Prawo Wielkich Liczb gwarantuje, że ![]() prawie na pewno, gdy
prawie na pewno, gdy ![]() .
W terminologii statystycznej,
.
W terminologii statystycznej, ![]() jest mocno zgodnym estymatorem obliczanej wielkości. Zadanie wydaje się rozwiązane. Są jednak dwa zasadnicze kłopoty.
jest mocno zgodnym estymatorem obliczanej wielkości. Zadanie wydaje się rozwiązane. Są jednak dwa zasadnicze kłopoty.
-
Estymator
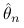 skonstruowany metodą CMC może się zbliżać do
skonstruowany metodą CMC może się zbliżać do 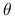 przerażająco wolno.
przerażająco wolno. -
Co robić, jeśli nie umiemy losować z rozkładu
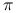 ?
?
8.1. Losowanie istotne
Zadziwiająco skutecznym sposobem na oba przedstawione wyżej kłopoty
jest losowanie istotne (Importance Sampling, w skrócie IS).
Przypuśćmy, że umiemy losować z rozkładu o gęstości ![]() . Zauważmy, że
. Zauważmy, że
gdzie ![]() . Piszemy tu wzory dla całek ale oczywiście dla sum jest tak samo.
Niech
. Piszemy tu wzory dla całek ale oczywiście dla sum jest tak samo.
Niech ![]() będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie
będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie ![]() ,
,
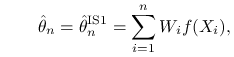 |
(8.1) |
gdzie
traktujemy jako wagi wylosowanych punktów ![]() .
Z tego co wyżej powiedzieliśmy wynika, że
.
Z tego co wyżej powiedzieliśmy wynika, że ![]() oraz
oraz
![]() prawie na pewno, gdy
prawie na pewno, gdy ![]() . Mamy więc estymator nieobciążony
i zgodny. Milcząco założyliśmy, że
. Mamy więc estymator nieobciążony
i zgodny. Milcząco założyliśmy, że ![]() w każdym wylosowanym punkcie, czyli, że
w każdym wylosowanym punkcie, czyli, że
![]() . Z tym zwykle nie ma wielkiego kłopotu.
Ponadto musimy założyć, że umiemy obliczać funkcję
. Z tym zwykle nie ma wielkiego kłopotu.
Ponadto musimy założyć, że umiemy obliczać funkcję ![]() w każdym wylosowanym punkcie.
Jeśli znamy tylko
w każdym wylosowanym punkcie.
Jeśli znamy tylko ![]() a nie znamy stałej
a nie znamy stałej ![]() to jest kłopot. Możemy tylko obliczyć
to jest kłopot. Możemy tylko obliczyć ![]() . Używamy zatem nieco innej postaci estymatora
IS, mianowicie
. Używamy zatem nieco innej postaci estymatora
IS, mianowicie
| (8.2) |
Ten estymator wygląda dziwnie, bo w mianowniku występuje estymator jedynki
ale chodzi o to, że we wzorze (8.2) w przeciwieństwie do (8.1)
możemy zastąpić ![]() przez
przez ![]() , bo nieznany czynnik
, bo nieznany czynnik ![]() skraca się.
Możemy jeszcze zapisać nasz estymator w zgrabnej formie
skraca się.
Możemy jeszcze zapisać nasz estymator w zgrabnej formie
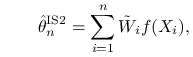 |
gdzie ![]() są unormowanymi wagami. Trzeba jednak
pamiętać, że to ,,unormowanie” polega na podzieleniu wag przez zmienną losową. W rezultacie
estymator
są unormowanymi wagami. Trzeba jednak
pamiętać, że to ,,unormowanie” polega na podzieleniu wag przez zmienną losową. W rezultacie
estymator ![]() jest obciążony. Jest jednak mocno zgodny, bo licznik
we wzorze (8.2) po podzieleniu przez
jest obciążony. Jest jednak mocno zgodny, bo licznik
we wzorze (8.2) po podzieleniu przez ![]() zmierza do
zmierza do ![]() a mianownik do 1,
prawie na pewno.
Estymator
a mianownik do 1,
prawie na pewno.
Estymator ![]() jest znacznie częściej używany niż
jest znacznie częściej używany niż ![]() . Oprócz uniezależnienia się od stałej normującej, jest jeszcze inny powód. Okazuje się, że (pomimo obciążenia)
estymator
. Oprócz uniezależnienia się od stałej normującej, jest jeszcze inny powód. Okazuje się, że (pomimo obciążenia)
estymator ![]() może być bardziej efektywny. Sens tego pojęcia wyjaśnimy w
następnym podrozdziale. Zarówno dobór przykładów jak i ogólny tok rozważań jest zapożyczony z monografii Liu [15].
może być bardziej efektywny. Sens tego pojęcia wyjaśnimy w
następnym podrozdziale. Zarówno dobór przykładów jak i ogólny tok rozważań jest zapożyczony z monografii Liu [15].
8.2. Efektywność estymatorów MC
Naturalne jest żądanie, aby estymator był mocno zgodny, ![]() prawie na pewno przy
prawie na pewno przy
![]() . Znaczy to, że zbliżymy się dowolnie blisko aproksymowanej wielkości, gdy tylko dostatecznie długo przedłużamy symulacje. Chcielibyśmy jednak wiedzieć coś konkretniejszego,
oszacować jak szybko błąd aproksymacji
. Znaczy to, że zbliżymy się dowolnie blisko aproksymowanej wielkości, gdy tylko dostatecznie długo przedłużamy symulacje. Chcielibyśmy jednak wiedzieć coś konkretniejszego,
oszacować jak szybko błąd aproksymacji ![]() maleje do zera i jakie
maleje do zera i jakie ![]() wystarczy
do osiągnięcia wystarczającej dokładności. Przedstawimy teraz
najprostsze i najczęściej stosowane w praktyce podejście, oparte na tzw. asymptotycznej
wariancji i konstrukcji asymptotycznych przedziałów ufności.
W typowej sytuacji estymator
wystarczy
do osiągnięcia wystarczającej dokładności. Przedstawimy teraz
najprostsze i najczęściej stosowane w praktyce podejście, oparte na tzw. asymptotycznej
wariancji i konstrukcji asymptotycznych przedziałów ufności.
W typowej sytuacji estymator ![]() ma następującą własność, nazywaną
asymptotyczną normalnością:
ma następującą własność, nazywaną
asymptotyczną normalnością:
w sensie zbieżności według rozkładu. W konsekwencji, dla ustalonej liczby ![]() ,
,
gdzie ![]() jest dystrybuantą rozkładu
jest dystrybuantą rozkładu ![]() . Często nie znamy asymptotycznej
wariancji
. Często nie znamy asymptotycznej
wariancji ![]() ale umiemy skonstruować jej zgodny estymator
ale umiemy skonstruować jej zgodny estymator ![]() .
Dla ustalonej ,,małej” dodatniej liczby
.
Dla ustalonej ,,małej” dodatniej liczby ![]() łatwo dobrać kwantyl rozkładu normalnego
łatwo dobrać kwantyl rozkładu normalnego ![]() tak, żeby
tak, żeby ![]() . Typowo
. Typowo
![]() i
i ![]() . Otrzymujemy
. Otrzymujemy
Ten wzór interpretuje się w praktyce tak: estymator ![]() ma błąd nie przekraczający
ma błąd nie przekraczający
![]() z prawdopodobieństwem około
z prawdopodobieństwem około ![]() . W żargonie statystycznym
. W żargonie statystycznym ![]() jest nazywane asymptotycznym poziomem ufności.
jest nazywane asymptotycznym poziomem ufności.
Chociaż opisame powyżej podejście ma swoje słabe strony, to prowadzi do prostego kryterium
porównywania estymatorów. Przypuśćmy, że mamy dwa estymatory ![]() i
i ![]() , oba asymptotycznie normalne, o asymptotycznej wariancji
, oba asymptotycznie normalne, o asymptotycznej wariancji ![]() i
i ![]() odpowiednio. Przypuśćmy dalej, że dla obliczenia pierwszego z tych estymatorów generujemy
odpowiednio. Przypuśćmy dalej, że dla obliczenia pierwszego z tych estymatorów generujemy
![]() punktów, zaś dla drugiego
punktów, zaś dla drugiego ![]() . Błędy obu estymatorów na tym mym poziomie istotności są ograniczone przez, odpowiednio,
. Błędy obu estymatorów na tym mym poziomie istotności są ograniczone przez, odpowiednio, ![]() i
i
![]() . Przyrównując te wyrażenia do siebie dochodzimy do wniosku, że oba estymatory osiągają podobną dokładność, jeśli
. Przyrównując te wyrażenia do siebie dochodzimy do wniosku, że oba estymatory osiągają podobną dokładność, jeśli
![]() . Liczbę
. Liczbę
nazywamy względną efektywnością (asymptotyczną). Czasami dobrze jest wybrać
za ,,naturalny punkt odniesienia” estymator CMC i zdefiniować efektywność
estymatora ![]() o asymptotycznej wariancji
o asymptotycznej wariancji ![]() jako
jako
Mówi się też, że jeśli wygenerujemy próbkę ![]() punktów i obliczymy
punktów i obliczymy ![]() to ,,efektywna liczność próbki” (ESS, czyli effective sample size) jest
to ,,efektywna liczność próbki” (ESS, czyli effective sample size) jest ![]() . Tyle
bowiem należałoby wygenerować punktów stosując CMC, żeby osiągnąć podobną dokładność.
. Tyle
bowiem należałoby wygenerować punktów stosując CMC, żeby osiągnąć podobną dokładność.
Asymptotyczna normalność prostego estymatora CMC wynika wprost z Centralnego Twierdzenia Granicznego (CTG). Istotnie, jeśli generujemy niezależnie
![]() o jednakowym rozkładzie
o jednakowym rozkładzie ![]() , to
, to
gdzie
Zupełnie podobnie, dla losowania istotnego w formie (8.1) otrzymujemy asymptotyczną normalność i przy tym
Z tego wzorku widać, że estymator może mieć wariancję zero jeśli
![]() . Niestety, żeby obliczyć
. Niestety, żeby obliczyć ![]() potrzebna jest znajomość
współczynnika proporcjonalności, który jest równy…
potrzebna jest znajomość
współczynnika proporcjonalności, który jest równy…![]() . Nie wszystko jednak stracone.
Pozostaje ważna reguła heurystyczna:
. Nie wszystko jednak stracone.
Pozostaje ważna reguła heurystyczna:
Gęstość ![]() należy tak dobierać, aby jej ,,kształt” był zbliżony do funkcji
należy tak dobierać, aby jej ,,kształt” był zbliżony do funkcji
![]() .
.
Dla drugiej wersji losowania istotnego, (8.2), asymptotyczna normalność wynika z następujących rozważań:
gdzie
Wyrażenie w kwadratowym nawiasie może być ujemne, jeśli jest duża dodatnia korelacja
zmiennych ![]() i
i ![]() . W tej sytuacji estymator IS2 jest lepszy od IS1. Okazuje się
więc rzecz na pozór paradoksalna: dzielenie przez estymator jedynki może poprawić estymator.
Poza tym oba estymatory IS1 i IS2 mogą mieć mniejszą (asymptotyczną) wariancję, niż CMC. Jeśli
efektywność jest większa niż 100%, to używa się czasem określenia ,,estymator superefektywny”.
. W tej sytuacji estymator IS2 jest lepszy od IS1. Okazuje się
więc rzecz na pozór paradoksalna: dzielenie przez estymator jedynki może poprawić estymator.
Poza tym oba estymatory IS1 i IS2 mogą mieć mniejszą (asymptotyczną) wariancję, niż CMC. Jeśli
efektywność jest większa niż 100%, to używa się czasem określenia ,,estymator superefektywny”.
Jeśli interesuje nas obliczenie wartości oczekiwanej dla wielu różnych funkcji ![]() , to
warto wprowadzić uniwersalny, niezależny of
, to
warto wprowadzić uniwersalny, niezależny of ![]() wskaźnik efektywności. Niezłym takim wskaźnikiem jest
wskaźnik efektywności. Niezłym takim wskaźnikiem jest ![]() .
Istotnie, ,,odchylenie
.
Istotnie, ,,odchylenie ![]() ” pomiędzy gęstością instrumentalną
” pomiędzy gęstością instrumentalną ![]() i docelową
i docelową ![]() , jest określone poniższym wzorem:
, jest określone poniższym wzorem:
Niestety, to ,,odchylenie” nie jest odległością, bo nie spełnia warunku symetrii.
Niemniej widać, że małe wartości ![]() świadczą o bliskości
świadczą o bliskości ![]() i
i ![]() .
Zauważmy, jeszcze, że
.
Zauważmy, jeszcze, że ![]() jest wariancją asymptotyczną estymatora
IS1 dla funkcji
jest wariancją asymptotyczną estymatora
IS1 dla funkcji ![]() .
.
Zgodnym estymatorem wielkości ![]() jest
jest
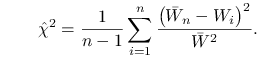 |
Dzielenie przez ![]() (a nie
(a nie ![]() ) wynika z tradycji. Dzielenie przez
) wynika z tradycji. Dzielenie przez ![]() powoduje, że
estymator nie wymaga znajomości czynnika normującego gęstość
powoduje, że
estymator nie wymaga znajomości czynnika normującego gęstość ![]() .
Jest to w istocie estymator typu IS2. Estymator typu IS1 jest równy po prostu
.
Jest to w istocie estymator typu IS2. Estymator typu IS1 jest równy po prostu ![]() , ale można go stosować tylko gdy znamy czynnik normujący.
, ale można go stosować tylko gdy znamy czynnik normujący.
Wprowadźmy teraz bardziej formalnie pojęcie ważonej próbki. Niech ![]() będzie
parą zmiennych losowych o wartościach w
będzie
parą zmiennych losowych o wartościach w ![]() . Jeśli rozkład brzegowy
. Jeśli rozkład brzegowy
![]() ma gęstość
ma gęstość ![]() zaś docelowa gęstość jest postaci
zaś docelowa gęstość jest postaci ![]() to żądamy aby
to żądamy aby
dla prawie wszystkich ![]() . Mówimy wtedy, że próbka jest dopasowana do rozkładu
. Mówimy wtedy, że próbka jest dopasowana do rozkładu ![]() . Idea jest taka jak w losowaniu istotnym IS2: dopasowanie gwarantuje, że dla każdej funkcji
. Idea jest taka jak w losowaniu istotnym IS2: dopasowanie gwarantuje, że dla każdej funkcji ![]() mamy
mamy ![]() . Nie jest konieczne, aby
. Nie jest konieczne, aby ![]() było deterministyczną funkcją
było deterministyczną funkcją ![]() . Pozostawiamy sobie możliwość generowania wag losowo.
. Pozostawiamy sobie możliwość generowania wag losowo.
Stała normująca ![]() jest na ogół nieznana, a więc
waga
jest na ogół nieznana, a więc
waga ![]() jest określona z dokładnością do proporcjonalności. W poprzednich
podrozdziałach dla podkreślenia opatrywaliśmy takie nieunormowane wagi znaczkiem ,,prim”
ale teraz to pomijamy.
Gdy generujemy ciąg ważonych zmiennych losowych
jest określona z dokładnością do proporcjonalności. W poprzednich
podrozdziałach dla podkreślenia opatrywaliśmy takie nieunormowane wagi znaczkiem ,,prim”
ale teraz to pomijamy.
Gdy generujemy ciąg ważonych zmiennych losowych ![]() , to
oczywiście wymaga się aby
, to
oczywiście wymaga się aby ![]() , gdzie
stała
, gdzie
stała ![]() musi być jednakowa dla wszystkich
musi być jednakowa dla wszystkich ![]() .
Jeśli założy się niezależność par
.
Jeśli założy się niezależność par ![]() , to zgodność i asymptotyczną normalność estymatora
, to zgodność i asymptotyczną normalność estymatora ![]() danego równaniem (8.2) wykazuje się tak samo jak poprzednio. Asymptotyczna wariancja jest równa
danego równaniem (8.2) wykazuje się tak samo jak poprzednio. Asymptotyczna wariancja jest równa
![]() ; czynnik
; czynnik ![]() pojawia się dlatego, że operujemy nieunormowanymi wagami.
pojawia się dlatego, że operujemy nieunormowanymi wagami.
Jest jednak dużo ciekawych zastosowań, w których
punkty ![]() są zależne. Wtedy nawet zgodność estymatora
są zależne. Wtedy nawet zgodność estymatora ![]() nie
jest automatyczna. Asymptotyczna normalność może zachodzić z graniczną
wariancją zupełnie inną niż w przypadku niezależnym lub nie zachodzić wcale.
nie
jest automatyczna. Asymptotyczna normalność może zachodzić z graniczną
wariancją zupełnie inną niż w przypadku niezależnym lub nie zachodzić wcale.
8.3. Ważona eliminacja
Interesujące jest powiązanie idei eliminacji z ważeniem próbek. Czysta metoda eliminacji pracuje w sytuacji, gdy gęstość ,,instrumentalna” majoryzuje funkcję proporcjonalną do gęstości docelowej, czyli ![]() . Jeśli ten warunek nie jest spełniony, to można
naprawić odpowiednio ważąc wylosowaną próbkę. Dokładniej, algorytm ważonej eliminacji
(Rejection Control, w skrócie RC) jest następujący.
. Jeśli ten warunek nie jest spełniony, to można
naprawić odpowiednio ważąc wylosowaną próbkę. Dokładniej, algorytm ważonej eliminacji
(Rejection Control, w skrócie RC) jest następujący.
| repeat |
| Gen |
| |
| if |
| begin |
| |
| Gen |
| end; |
| until ( |
Dowód poprawności algorytmu
Zauważmy, że prawdopodobieństwo akceptacji ![]() w tym algorytmie jest równe
w tym algorytmie jest równe ![]() , gdzie
, gdzie
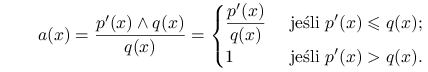 |
Rozkład ![]() na wyjściu algorytmu ma zatem gęstość
na wyjściu algorytmu ma zatem gęstość ![]() . Waga
. Waga
![]() jest więc ,,dopasowana” do rozkładu
jest więc ,,dopasowana” do rozkładu ![]() w sensie zdefiniowanym w poprzednim podrozdziale, bo
w sensie zdefiniowanym w poprzednim podrozdziale, bo
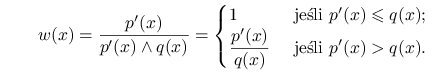 |
Zauważmy jeszcze, jak należy modyfikować wagi w RC, jeśli na wejściu mamy próbkę ważoną,
dopasowaną do ![]() .
Jeżeli punkt
.
Jeżeli punkt ![]() , pochodzący z rozkładu
, pochodzący z rozkładu ![]() , ma na wejściu wagę
, ma na wejściu wagę ![]() , to
na wyjściu zaakceptowany punkt
, to
na wyjściu zaakceptowany punkt ![]() ma rozkład
ma rozkład ![]() i powinien mieć wagę
i powinien mieć wagę ![]() . Widać stąd, że
. Widać stąd, że
gdzie ![]() jest napisanym wyżej prawdopodobieństwem akceptacji w RC.
jest napisanym wyżej prawdopodobieństwem akceptacji w RC.
Przykład 8.1 (Nie-samo-przecinające się błądzenia)
Po angielsku nazywają się Self Avoiding Walks, w skrócie SAW. Niech ![]() będzie
będzie ![]() -wymiarową kratą całkowitoliczbową.
Mówimy, że ciąg
-wymiarową kratą całkowitoliczbową.
Mówimy, że ciąg ![]() punktów kraty jest SAW-em jeśli
punktów kraty jest SAW-em jeśli
-
każde dwa kolejne punkty
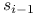 i
i 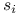 sąsiadują ze sobą, czyli różnią się
o
sąsiadują ze sobą, czyli różnią się
o 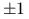 na dokładnie jednej współrzędnej,
na dokładnie jednej współrzędnej, -
żadne dwa punkty nie zajmują tego samego miejsca, czyli
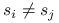 dla
dla 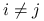 .
.
Zbiór wszystkich SAW-ów o ![]() ogniwach w
ogniwach w ![]() oznaczymy
oznaczymy ![]() , a
dla
, a
dla ![]() i
i ![]() ustalonych w skrócie SAW. Przykład
ustalonych w skrócie SAW. Przykład ![]() widać na rysunku.
widać na rysunku.
-
Jak policzyć SAW-y, czyli obliczyć
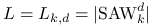 ?
?
Zainteresujmy się teraz ,,losowo wybranym SAW-em”. Rozumiemy przez to zmienną losową ![]() o rozkładzie jednostajnym w zbiorze
o rozkładzie jednostajnym w zbiorze ![]() , czyli taką, że
, czyli taką, że ![]() dla każdego
dla każdego ![]() . W skrócie,
. W skrócie, ![]() .
Niech
.
Niech ![]() oznacza odległość euklidesową końca SAW-a, czyli punktu
oznacza odległość euklidesową końca SAW-a, czyli punktu ![]() , od początku, czyli punktu
, od początku, czyli punktu ![]() . Na przykład dla lańcuszka widocznego na rysunku mamy
. Na przykład dla lańcuszka widocznego na rysunku mamy ![]() .
Można zadać sobie pytanie, jaka jest średni kwadrat takiej odległości, czyli
.
Można zadać sobie pytanie, jaka jest średni kwadrat takiej odległości, czyli
-
Jak obliczyć
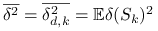 ,
przy założeniu, że
,
przy założeniu, że 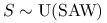 ?
?
Można zastosować prostą metodę MC, czyli eliminację. Niech ![]() oznacza zbiór
wszystkich ,,błądzeń”, czyli ciągów
oznacza zbiór
wszystkich ,,błądzeń”, czyli ciągów ![]() niekonieczne spełniających
warunek ,,
niekonieczne spełniających
warunek ,,![]() dla
dla ![]() ”. Oczywiście
”. Oczywiście ![]() i metoda generowania ,,losowego błądzenia” (z rozkładu
i metoda generowania ,,losowego błądzenia” (z rozkładu ![]() ) jest bardzo prosta: kolejno losujemy pojedyncze kroki, wybierając zawsze jedną z
) jest bardzo prosta: kolejno losujemy pojedyncze kroki, wybierając zawsze jedną z ![]() możliwości.
Żeby otrzymać ,,losowy SAW”, stosujemy eliminację. Ten sposób pozwala w zasadzie estymować
możliwości.
Żeby otrzymać ,,losowy SAW”, stosujemy eliminację. Ten sposób pozwala w zasadzie estymować
![]() (przez uśrednianie długości zaakceptowanych błądzeń) oraz
(przez uśrednianie długości zaakceptowanych błądzeń) oraz
![]() (przez zanotowanie frakcji akceptowanych błądzeń).
Niestety, metoda jest bardzo nieefektywna, bo dla dużych
(przez zanotowanie frakcji akceptowanych błądzeń).
Niestety, metoda jest bardzo nieefektywna, bo dla dużych ![]() prawdopodobieństwo akceptacji szybko zbliża sie do zera.
prawdopodobieństwo akceptacji szybko zbliża sie do zera.
Metoda ,,wzrostu” zaproponowana przez Rosenbluthów polega na losowaniu kolejnych kroków błądzenia spośród ,,dopuszczalnych punktów”, to znaczy punktów wcześniej nie odwiedzonych.
W każdym kroku, z wyjątkiem pierwszego mamy co najwyżej ![]() możliwości. W błądzeniu
widocznym na rysunku kolejne kroki wybieraliśmy spośród:
możliwości. W błądzeniu
widocznym na rysunku kolejne kroki wybieraliśmy spośród:
możliwych. Nasz SAW został zatem wylosowany z prawdopodobieństwem
Powiedzmy ogólniej, że przy budowaniu SAW-a ![]() mamy kolejno
mamy kolejno
możliwości (nie jest przy tym wykluczone, że w pewnym kroku nie mamy żadnej możliwości, ![]() ).
Używając terminologii i oznaczeń związanych z losowaniem istotnym powiemy, że
).
Używając terminologii i oznaczeń związanych z losowaniem istotnym powiemy, że
jest gęstością instrumentalną dla ![]() , gęstość docelowa jest stała, równa
, gęstość docelowa jest stała, równa
![]() , zatem funkcja podziału jest po prostu liczbą SAW-ów:
, zatem funkcja podziału jest po prostu liczbą SAW-ów: ![]() .
Wagi przypisujemy zgodnie ze wzorem
.
Wagi przypisujemy zgodnie ze wzorem ![]() (jeśli wygenerowanie
SAW-a się nie udało,
(jeśli wygenerowanie
SAW-a się nie udało, ![]() dla pewnego
dla pewnego ![]() , to waga jest zero).
Niech teraz
, to waga jest zero).
Niech teraz ![]() będą niezależnymi błądzeniami losowanymi
metodą Rosenbluthów. Zgodnie z ogólnymi zasadami losowania istotnego,
będą niezależnymi błądzeniami losowanymi
metodą Rosenbluthów. Zgodnie z ogólnymi zasadami losowania istotnego,
Należy przy tym uwzględniać w tych wzorach błądzenia o wadze zero, czyli ,,nieudane SAW-y”.
Przykład 8.2 (Prawdopodobieństwo ruiny i wykładnicza zamiana miary)
Rozpatrzymy najprostszy model procesu opisującego straty i przychody w ubezpieczeniowej ,,teorii ryzyka”. Niech ![]() będą zmiennymi losowymi oznaczającymi straty netto
(straty
będą zmiennymi losowymi oznaczającymi straty netto
(straty ![]() przychody) towarzystwa ubezpieczeniowego w kolejnych okresach czasu. Założymy
(co jest dużym uproszczeniem), że te zmienne są niezależne i mają jednakowy rozkład o gęstości
przychody) towarzystwa ubezpieczeniowego w kolejnych okresach czasu. Założymy
(co jest dużym uproszczeniem), że te zmienne są niezależne i mają jednakowy rozkład o gęstości
![]() . Tak zwana ,,nadwyżka ubezpieczyciela” na koniec
. Tak zwana ,,nadwyżka ubezpieczyciela” na koniec ![]() -go roku jest równa
-go roku jest równa
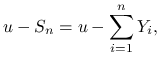 |
gdzie ![]() jest rezerwą początkową.
Interesuje nas prawdopodobieństwo zdarzenia, polegającego na tym, że
jest rezerwą początkową.
Interesuje nas prawdopodobieństwo zdarzenia, polegającego na tym, że
![]() dla pewnego
dla pewnego ![]() . Mówimy wtedy (znowu w dużym uproszczeniu) o ,,ruinie ubezpieczyciela”. Wygodnie jest przyjąć następujące oznaczenia i konwencje.
Zmienna losowa
. Mówimy wtedy (znowu w dużym uproszczeniu) o ,,ruinie ubezpieczyciela”. Wygodnie jest przyjąć następujące oznaczenia i konwencje.
Zmienna losowa
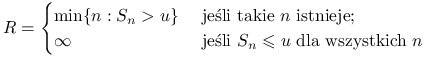 |
oznacza czas oczekiwania na ruinę, przy czym jeśli ruina nigdy nie nastąpi to ten czas uznajemy za nieskończony. Przy takiej umowie, prawdopodobieństwo ruiny możemy zapisać jako ![]() .
Wskaźnik
.
Wskaźnik ![]() przy symbolu wartości oczekiwanej przypomina, że chodzi tu o ,,oryginalny” proces,
dla którego
przy symbolu wartości oczekiwanej przypomina, że chodzi tu o ,,oryginalny” proces,
dla którego ![]() .
.
Obliczenie ![]() analitycznie jest możliwe tylko w bardzo specjalnych przykładach. Motody numeryczne istnieją, ale też nie są łatwe. Pokażemy sposób obliczania
analitycznie jest możliwe tylko w bardzo specjalnych przykładach. Motody numeryczne istnieją, ale też nie są łatwe. Pokażemy sposób obliczania ![]() metodą Monte Carlo, który stanowi jeden z najpiękniejszych, klasycznych, przykładów losowania istotnego.
Przyjmiemy bardzo rozsądne założenie, że
metodą Monte Carlo, który stanowi jeden z najpiękniejszych, klasycznych, przykładów losowania istotnego.
Przyjmiemy bardzo rozsądne założenie, że ![]() . Funkcję tworzącą momenty, która odpowiada gęstości
. Funkcję tworzącą momenty, która odpowiada gęstości ![]() określamy wzorem
określamy wzorem
Założymy, że ta funkcja przyjmuje wartości skończone przynajmniej w pewnym otoczeniu zera
i istnieje takie ![]() , że
, że
Liczba ![]() jest nazywana współczynnikiem dopasowania i odgrywa tu kluczową rolę.
jest nazywana współczynnikiem dopasowania i odgrywa tu kluczową rolę.
Metoda wykładniczej zamiany miary jest specjalnym przypadkiem losowania istotnego. Zeby określić instrumentalny rozkład prawdopodobieństwa, połóżmy
Z definicji współczynnika dopasowania wynika, że ![]() jest gęstością prawdopodobieństwa, to znaczy
jest gęstością prawdopodobieństwa, to znaczy
![]() .
Generuje się ciąg
.
Generuje się ciąg ![]() jednakowo rozłożonych zmiennych losowych o gęstości
jednakowo rozłożonych zmiennych losowych o gęstości ![]() .
Dla utworzonego w ten sposób ,,instrumentalnego procesu” używać będziemy symboli
.
Dla utworzonego w ten sposób ,,instrumentalnego procesu” używać będziemy symboli ![]() i
i
![]() . Zauważmy, że
. Zauważmy, że
ponieważ funkcja tworząca momenty ![]() jest wypukła,
jest wypukła, ![]() i
i ![]() . Po zamianie miary, proces
. Po zamianie miary, proces ![]() na mocy Prawa Wielkich Liczb
zmierza prawie na pewno do minus nieskończoności, a zatem ruina następuje z prawdopodobieństwem jeden,
na mocy Prawa Wielkich Liczb
zmierza prawie na pewno do minus nieskończoności, a zatem ruina następuje z prawdopodobieństwem jeden,
![]() . Pokażemy, jak wyrazić prstwo ruiny dla oryginalnego procesu w
terminach procesu instrumentalnego. Niech
. Pokażemy, jak wyrazić prstwo ruiny dla oryginalnego procesu w
terminach procesu instrumentalnego. Niech
Innymi słowy, zdarzenie ![]() zachodzi gdy
zachodzi gdy ![]() .
Mamy zatem
.
Mamy zatem
Weźmy sumę powyższych równości dla ![]() i skorzystajmy z faktu, że
i skorzystajmy z faktu, że ![]() . Dochodzimy do wzoru
. Dochodzimy do wzoru
| (8.3) |
Ten fakt jest podstawą algorytmu Monte Carlo:
| for |
| begin |
| |
| repeat |
| Gen |
| until |
| |
| end |
Algorytm jest prosty i efektywny. Trochę to zadziwiające, że w celu obliczenia prawdopodobieństwa
ruiny generuje się proces dla którego ruina jest pewna. Po chwili zastanowienia można jednak zauważyć,
że wykładnicza zamiana miary realizuje podstawową ideę losowania istotnego: rozkład instrumentalny
,,naśladuje” proces docelowy ograniczony do zdarzenia ![]() .
.
Ciekawe, że wykładnicza zamiana miary nie tylko jest techniką Monte Carlo, ale jest też
techniką dowodzenia twierdzeń! Aby się o tym przekonać, zauważmy, że ,,po drodze”
udowodniliśmy nierówność ![]() (wynika to z podstawowego wzoru
(8.3) gdyż
(wynika to z podstawowego wzoru
(8.3) gdyż ![]() ).
Jest to sławna nierówność Lundberga i wcale nie jest ona oczywista.
).
Jest to sławna nierówność Lundberga i wcale nie jest ona oczywista.