9. Algorytmy Monte Carlo II. Redukcja wariancji
W tym rozdziale omówię niektóre metody redukcji wariancji dla klasycznych algorytmów Monte Carlo, w których
losujemy próbki niezależnie, z jednakowego rozkładu. Wiemy, że dla takich algorytmów wariancja
estymatora zachowuje się jak ![]() . Jedyne, co możemy zrobić – to konstruować takie algorytmy,
dla których stała ,,
. Jedyne, co możemy zrobić – to konstruować takie algorytmy,
dla których stała ,,![]() ” jest możliwie mała. Najważniejszą z tych metod faktycznie już poznaliśmy:
jest to losowanie istotne, omówione w Rozdziale 8. Odpowiedni wybór ,,rozkładu
instrumentalnego” może zmniejszyć wariancję…setki tysięcy razy! Istnieje jeszcze kilka
innych, bardzo skutecznych technik. Do podstawowych należą: losowanie warstwowe, metoda zmiennych kontrolnych, metoda
zmiennych antytetycznych. Możliwe są niezliczone modyfikacje i kombinacje tych metod.
Materiał zawarty w tym rozdziale jest w dużym stopniu zaczerpnięty z monografii Ripleya [18].
” jest możliwie mała. Najważniejszą z tych metod faktycznie już poznaliśmy:
jest to losowanie istotne, omówione w Rozdziale 8. Odpowiedni wybór ,,rozkładu
instrumentalnego” może zmniejszyć wariancję…setki tysięcy razy! Istnieje jeszcze kilka
innych, bardzo skutecznych technik. Do podstawowych należą: losowanie warstwowe, metoda zmiennych kontrolnych, metoda
zmiennych antytetycznych. Możliwe są niezliczone modyfikacje i kombinacje tych metod.
Materiał zawarty w tym rozdziale jest w dużym stopniu zaczerpnięty z monografii Ripleya [18].
9.1. Losowanie warstwowe
Tak jak w poprzednim rozdziale, zedanie polega na obliczeniu wielkości
| (9.1) |
gdzie rozkład prawdopodobieństwa i jego gęstość dla uproszczenia oznaczamy tym samym symbolem ![]() . Losowanie warstwowe polega na tym, że rozbijamy przestrzeń
. Losowanie warstwowe polega na tym, że rozbijamy przestrzeń ![]() na
sumę
na
sumę ![]() rozłącznych podzbiorów (warstw),
rozłącznych podzbiorów (warstw),
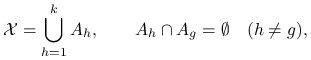 |
(9.2) |
i losujemy ![]() niezależnych próbek, po jednej z każdej warstwy. Niech
niezależnych próbek, po jednej z każdej warstwy. Niech ![]() będzie gęstostością rozkładu warunkowego
zmiennej
będzie gęstostością rozkładu warunkowego
zmiennej ![]() przy
przy ![]() , czyli
, czyli
| (9.3) |
Widać natychmiast, że ![]() . Rozbijamy teraz całkę, którą chcemy obliczyć:
. Rozbijamy teraz całkę, którą chcemy obliczyć:
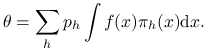 |
(9.4) |
Możemy użyć następującego estymatora warstwowego:
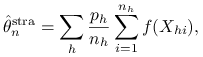 |
(9.5) |
gdzie
| (9.6) |
jest próbką rozmiaru ![]() wylosowaną z
wylosowaną z ![]() -tej warstwy (
-tej warstwy (![]() ).
Jest to estymator nieobciążony,
).
Jest to estymator nieobciążony,
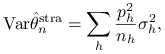 |
(9.7) |
gdzie ![]() .
.
Porównajmy estymator warstwowy (9.5) ze ,,zwykłym” estymatorem
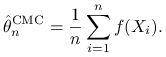 |
(9.8) |
opartym na jednej próbce
| (9.9) |
Oczywiście
| (9.10) |
gdzie ![]() . Żeby porównanie było ,,uczciwe” rozważmy próbkę liczności
. Żeby porównanie było ,,uczciwe” rozważmy próbkę liczności ![]() .
Jeśli decydujemy się na sumaryczną liczność
próbki
.
Jeśli decydujemy się na sumaryczną liczność
próbki ![]() , to możemy w różny sposób ,,rozdzielić” to
, to możemy w różny sposób ,,rozdzielić” to ![]() pomiędzy warstwami. To się nazywa alokacja próbki.
pomiędzy warstwami. To się nazywa alokacja próbki.
Stwierdzenie 9.1 (Alokacja proporcjonalna)
Jeżeli ![]() dla
dla ![]() , to
, to
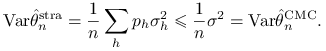 |
(9.11) |
Dowód
Wyrażenie na wariancję wynika znatychmiast z podstawienia ![]() w ogólnym wzorze (9.7).
Nierówność wynika z następującej tożsamości:
w ogólnym wzorze (9.7).
Nierówność wynika z następującej tożsamości:
| (9.12) |
gdzie ![]() . Jest to klasyczny wzór na dekompozycję wariancji na
,,wariancję wewnątrz warstw” (pierwszy składnik w (9.12)) i ,,wariancję pomiędzy warstwami”
(drugi składnik w (9.12)). Zdefiniujemy zmienną losową
. Jest to klasyczny wzór na dekompozycję wariancji na
,,wariancję wewnątrz warstw” (pierwszy składnik w (9.12)) i ,,wariancję pomiędzy warstwami”
(drugi składnik w (9.12)). Zdefiniujemy zmienną losową ![]() jako ,,numer warstwy do której wpada
jako ,,numer warstwy do której wpada
![]() ”, czyli
”, czyli ![]() . Możemy teraz wzór (9.12) przepisać w dobrze znanej postaci
. Możemy teraz wzór (9.12) przepisać w dobrze znanej postaci
| (9.13) |
Wzór (9.12) podpowiada, jak dzielić przestrzeń na warstwy. Największy zysk w porównaniu z losowaniem
nie-warstwowym jest wtedy, gdy ,,wariancja międzywarstwowa” jest dużo większa od ,,wewnątrzwarstwowej” Warstwy należy więc
wybierać tak, żeby funkcja ![]() była możliwie bliska stałej na każdym zbiorze
była możliwie bliska stałej na każdym zbiorze ![]() i różniła
się jak najbardziej pomiędzy poszczególnymi zbiorami.
i różniła
się jak najbardziej pomiędzy poszczególnymi zbiorami.
Stwierdzenie 9.1 pokazuje, że zawsze zyskujemy na losowaniu warstwowym, jeśli zastosujemy najprostszą,
proporcjonalną alokację. Okazuje się, że nie jest to alokacja najlepsza.
Jerzy Spława-Neyman odkrył prostą regułę wyznaczania alokacji optymalnej. Wychodzimy od wzoru (9.7) i
staramy się zoptymalizować prawą stronę przy warunku ![]() . Poszukujemy zatem rozwiązania
zadania
. Poszukujemy zatem rozwiązania
zadania
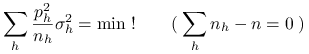 |
(9.14) |
(względem zmiennych ![]() ). Zastosujmy metodę mnożników Lagrange'a. Szukamy minimum
). Zastosujmy metodę mnożników Lagrange'a. Szukamy minimum
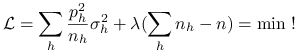 |
(9.15) |
Obliczamy pochodną i przyrównujemy do zera:
| (9.16) |
Stąd natychmiast otrzymujemy rozwiązanie:
![]() .
.
Stwierdzenie 9.2 (Alokacja optymalna, J. Neyman)
Estymator warstwowy ma najmniejszą wariancję jeśli alokacja ![]() losowanych punktów jest dana wzorem
losowanych punktów jest dana wzorem
| (9.17) |
Zignorowaliśmy tutaj niewygodne wymaganie, że liczności próbek ![]() muszą być całkowite. Gdyby to wziąć pod uwagę,
rozwiązanie stałoby się skomplikowane, a zysk praktyczny z tego byłby znikomy. W praktyce rozwiązanie neymanowskie
zaokrągla się do liczb całkowitych i koniec. Ważniejszy jest inny problem. Żeby wyznaczyć alokację optymalną,
trzeba znać nie tylko prawdopodobieństwa
muszą być całkowite. Gdyby to wziąć pod uwagę,
rozwiązanie stałoby się skomplikowane, a zysk praktyczny z tego byłby znikomy. W praktyce rozwiązanie neymanowskie
zaokrągla się do liczb całkowitych i koniec. Ważniejszy jest inny problem. Żeby wyznaczyć alokację optymalną,
trzeba znać nie tylko prawdopodobieństwa ![]() ale i wariancje warstwowe
ale i wariancje warstwowe ![]() . W praktyce często opłaca się wylosować
wstępne próbki, na podstawie których estymuje się wariancje
. W praktyce często opłaca się wylosować
wstępne próbki, na podstawie których estymuje się wariancje ![]() . Dopiero potem alokuje się dużą,
roboczą próbkę rozmiaru
. Dopiero potem alokuje się dużą,
roboczą próbkę rozmiaru ![]() , która jest wykorzystana do obliczania docelowej całki.
, która jest wykorzystana do obliczania docelowej całki.
9.2. Zmienne kontrolne
Idea zmiennych kontrolnych polega na rozbiciu docelowej całki (wartości oczekiwanej) na dwa składniki, z których jeden umiemy obliczyć analitycznie. Metodę Monte Carlo stosujemy do drugiego składnika. Przedstawmy wielkość obliczaną w postaci
| (9.18) |
Dążymy do tego, żeby całka funkcji ![]() była obliczona analitycznie (lub numerycznie) a różnica
była obliczona analitycznie (lub numerycznie) a różnica ![]() była
możliwie bliska stałej, bo wtedy wariancja metody Monte Carlo jest mała. Funkcję
była
możliwie bliska stałej, bo wtedy wariancja metody Monte Carlo jest mała. Funkcję ![]() lub zmienną losową
lub zmienną losową
![]() nazywamy zmienną kontrolną.
nazywamy zmienną kontrolną.
Dla uproszczenia połóżmy ![]() , gdzie
, gdzie ![]() . Przypuśćmy, że zmiennej kontrolnej będziemy szukać pośród
kombinacji liniowych funkcji
. Przypuśćmy, że zmiennej kontrolnej będziemy szukać pośród
kombinacji liniowych funkcji ![]() o znanych całkach. Niech
o znanych całkach. Niech ![]() i
i ![]() .
Przy tym stale pamiętajmy, że
.
Przy tym stale pamiętajmy, że ![]() i będziemy pomijać indeks
i będziemy pomijać indeks ![]() przy wartościach oczekiwanych i wariancjach. Zatem
przy wartościach oczekiwanych i wariancjach. Zatem
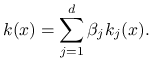 |
(9.19) |
Innymi słowy poszukujemy wektora współczynników ![]() który minimalizuje wariancję
który minimalizuje wariancję
![]() . Wykorzystamy następujący standardowy wynik z teorii regresji liniowej.
. Wykorzystamy następujący standardowy wynik z teorii regresji liniowej.
Stwierdzenie 9.3
Niech ![]() i
i ![]() będą zmiennymi losowymi o skończonych drugich momentach, wymiaru odpowiednio
będą zmiennymi losowymi o skończonych drugich momentach, wymiaru odpowiednio ![]() i
i ![]() .
Zakładamy dodatkowo odwracalność macierzy wariancji-kowariancji
.
Zakładamy dodatkowo odwracalność macierzy wariancji-kowariancji ![]() . Kowariancję pomiędzy
. Kowariancję pomiędzy
![]() i
i ![]() traktujemy jako wektor wierszowy i oznaczamy przez
traktujemy jako wektor wierszowy i oznaczamy przez ![]() Spośród zmiennych losowych postaci
Spośród zmiennych losowych postaci ![]() , najmniejszą wariancję otrzymujemy dla
, najmniejszą wariancję otrzymujemy dla
| (9.20) |
Ta najmniejsza wartość wariancji jest równa
| (9.21) |
Przepiszmy tem wynik w bardziej sugestywnej formie. Niech ![]() . Można pokazać, że
. Można pokazać, że ![]() maksymalizuje
korelację pomiędzy
maksymalizuje
korelację pomiędzy ![]() i
i ![]() . Napiszmy
. Napiszmy
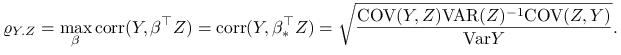 |
(9.22) |
Niech teraz ![]() będzie estymatorem zmiennych kontrolnych. To znaczy, że losujemy próbkę
będzie estymatorem zmiennych kontrolnych. To znaczy, że losujemy próbkę ![]() ,
,
| (9.23) |
gdzie ![]() , zaś
, zaś ![]() są obliczone analitycznie lub numerycznie
są obliczone analitycznie lub numerycznie
![]() . Wariancja estymatora jest wyrażona wzorem
. Wariancja estymatora jest wyrażona wzorem
| (9.24) |
co należy porównać z wariancją ![]() ,,zwykłego” estymatora.
,,zwykłego” estymatora.
Zróbmy podobną uwagę, jak w poprzednim podrozdziale. Optymalny wybór współczynników regresji wymaga znajomości wariancji i kowariancji, których obliczenie może być …(i jest zazwyczaj!) trudniejsze niż wyjściowe zadanie obliczenia wartości oczekiwanej. Niemniej, można najpierw wylosować wstępną próbkę, wyestymować potrzebne wariancje i kowariancje (nawet niezbyt dokładnie) po to, żeby dla dużej, roboczej próbki skonstruować dobre zmienne kontrolne.
Wspomnijmy na koniec, że dobieranie zmiennej kontrolnej metodą regresji liniowej nie jest jedynym sposobem. W konkretnych przykładach można spotkać najróżniejsze, bardzo pomysłowe konstrukcje, realizujące podstawową ideę zmiennych kontrolnych.
9.3. Zmienne antytetyczne
Przypuśćmy, że estymujemy wielkość ![]() . Jeśli mamy dwie zmienne losowe
. Jeśli mamy dwie zmienne losowe ![]() i
i ![]() o jednakowym rozkładzie
o jednakowym rozkładzie ![]() ale nie zakładamy ich niezależności, to
ale nie zakładamy ich niezależności, to
Jeśli ![]() , to wariancja w powyższym wzorze jest mniejsza niż
, to wariancja w powyższym wzorze jest mniejsza niż ![]() , czyli
mniejsza niż w przypadku niezależności
, czyli
mniejsza niż w przypadku niezależności ![]() i
i ![]() . To sugeruje, żeby zamiast losować niezależnie
. To sugeruje, żeby zamiast losować niezależnie ![]() zmiennych
zmiennych
![]() , wygenerować pary zmiennych ujemnie skorelowanych. Załóżmy, że
, wygenerować pary zmiennych ujemnie skorelowanych. Załóżmy, że ![]() i mamy
i mamy ![]() niezależnych par
niezależnych par
![]() , a więc łącznie
, a więc łącznie ![]() zmiennych. Porównajmy wariancję ,,zwykłego” estymatora
zmiennych. Porównajmy wariancję ,,zwykłego” estymatora
![]() i estymatora
i estymatora ![]() wykorzystującego ujemne skorelowanie par:
wykorzystującego ujemne skorelowanie par:
Wariancja estymatora ![]() jest tym mniejsza, im
jest tym mniejsza, im ![]() bliższe
bliższe ![]() (im bardziej ujemnie skorelowane są pary). Standardowym sposobem generowania ujemnie skorelowanych
par jest odwracanie dystrybuanty z użyciem ,,odwróconych loczb losowych”.
(im bardziej ujemnie skorelowane są pary). Standardowym sposobem generowania ujemnie skorelowanych
par jest odwracanie dystrybuanty z użyciem ,,odwróconych loczb losowych”.
Stwierdzenie 9.4
Jeśli ![]() jest funkcją monotoniczną różną od stałej,
jest funkcją monotoniczną różną od stałej, ![]() i
i ![]() , to
, to
| (9.25) |
Dowód
Bez straty ogólności załóżmy, że ![]() jest niemalejąca. Niech
jest niemalejąca. Niech
![]() i
i ![]() . Łatwo zauważyć, że
. Łatwo zauważyć, że
![]() . Zauważmy, że
. Zauważmy, że
| (9.26) |
ponieważ dla ![]() mamy
mamy ![]() i dla
i dla ![]() mamy
mamy ![]() .
.
Przypomnijmy, że dla dowolnej dystrybuanty ![]() określamy uogólnioną funkcję odwrotną
określamy uogólnioną funkcję odwrotną ![]() następującym wzorem:
następującym wzorem:
| (9.27) |
Natychmiast wnioskujemy ze Stwierdzenia 9.4, że
![]() . W ten sposób możemy produkować ujemnie skorelowane pary zmiennych
o zadanej dystrybuancie. Okazuje się, że są to najbardziej ujemnie skorelowane pary. Jeśli
. W ten sposób możemy produkować ujemnie skorelowane pary zmiennych
o zadanej dystrybuancie. Okazuje się, że są to najbardziej ujemnie skorelowane pary. Jeśli
![]() i
i ![]() , to
, to
| (9.28) |
Powyższy fakt ma oczywiste znaczenie z punktu widzenia metod Monte Carlo. Udowodnimy ogólniejsze twierdzenie.
Twierdzenie 9.1
Jeżeli ![]() ,
, ![]() oraz
oraz ![]() ,
, ![]() to
to
| (9.29) |
Twierdzenie 9.2 wynika z trzech poniższych faktów. Każdy z nich jest sam w sobie interesujący. Zaczniemy od sławnego wyniku Frecheta.
Twierdzenie 9.2 (Ograniczenia Frecheta)
Jeżeli ![]() ,
, ![]() oraz
oraz ![]() oznaczają,
odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę dwóch zmiennych losowych to
oznaczają,
odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę dwóch zmiennych losowych to
| (9.30) |
Istnieją rozkłady łączne o brzegowych ![]() i
i ![]() , dla których jest osiągane
ograniczenie dolne i ograniczenie górne.
, dla których jest osiągane
ograniczenie dolne i ograniczenie górne.
Dowód
Ograniczenie górne wynika z oczywistych nierówności
| (9.31) |
Ograniczenie dolne jest równie proste:
| (9.32) |
Pozostała do pokazania osiągalność. Następujący lemat jest jednym z piękniejszych przykładów ,,symulacyjnego punktu widzenia” w rachunku prawdopodobieństwa.
Lemat 9.1
Jeśli ![]() to
to
| (9.33) |
Dowód
Pierwsza równość jest oczywista:
| (9.34) |
Druga równość też jest oczywista:
| (9.35) |
Głębokie twierdzenie Frecheta składa się więc z kilku dość oczywistych spostrzeżeń. Zeby udowodnić Twierdzenie 9.1 potrzeba jeszcze jednego ciekawego lematu.
Lemat 9.2
Niech ![]() ,
, ![]() i
i ![]() oznaczają,
odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę zmiennych losowych
oznaczają,
odpowiednio, dystrybuanty brzegowe oraz łączną dystrybuantę zmiennych losowych ![]() i
i ![]() .
Jeśli
.
Jeśli ![]() ,
, ![]() to
to
| (9.36) |
Dowód
Niech ![]() i
i ![]() będą niezależnymi parami o jednakowym rozkładzie
takim jak para
będą niezależnymi parami o jednakowym rozkładzie
takim jak para ![]() . Wtedy
. Wtedy
| (9.37) |




