Zagadnienia
3. Analiza Składowych Głównych
3.1. Analiza danych wielowymiarowych
Oznaczenia:
-
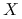 będzie oznaczał wektor losowy w przestrzeni
będzie oznaczał wektor losowy w przestrzeni 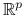 :
: ![X=\left(\begin{array}[]{c}X_{1}\\
\ldots\\
X_{p}\\
\end{array}\right)](wyklady/st2/mi/mi360.png) .
. -
Przez
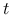 oznaczymy wektor liczb,
oznaczymy wektor liczb, 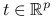 .
. -
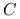 to macierz liczb:
to macierz liczb: 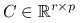 .
. -
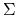 będzie oznaczać macierz kowariancji wektora losowego
będzie oznaczać macierz kowariancji wektora losowego 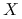 , czyli:
, czyli: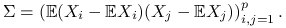
Oznaczeń
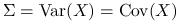 będziemy używać zamiennie.
będziemy używać zamiennie.
Stwierdzenie 3.1
Proste własności wprowadzonych pojęć:
-
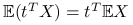 ,
, 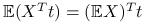 .
. -
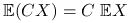 , gdzie:
, gdzie:![C=\left(\begin{array}[]{c}C_{1}^{T}\\
\ldots\\
C_{r}^{T}\\
\end{array}\right),\quad\mathbb{E}(CX)\stackrel{(1)}{=}\left(\begin{array}[]{c}C_{1}^{T}\\
\ldots\\
C_{r}^{T}\\
\end{array}\right)\mathbb{E}X](wyklady/st2/mi/mi316.png)
.
-
Macierz kowariancji jest równa:
![\Sigma=\mathbb{E}\left[(X-\mathbb{E}X)(X-\mathbb{E}X)^{T}\right].](wyklady/st2/mi/mi223.png)
-
Macierz kowariancji ma następującą własność:
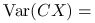
![\displaystyle\mathbb{E}\left[(CX-\mathbb{E}CX)(CX-\mathbb{E}CX)^{T}\right]=](wyklady/st2/mi/mi231.png)
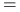
![\displaystyle\mathbb{E}\left[C(X-\mathbb{E}X)(X-\mathbb{E}X)^{T}C^{T}\right]=](wyklady/st2/mi/mi275.png)
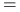
![\displaystyle C\text{ }\mathbb{E}\left[(X-\mathbb{E}X)(X-\mathbb{E}X)^{T}\right]C^{T}=](wyklady/st2/mi/mi354.png)
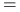
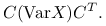
-
Ponadto, macierz
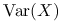 jest symetryczna i nieujemnie określona:
jest symetryczna i nieujemnie określona:symetryczność wynika z symetryczności kowariancji dwóch zmiennych losowych;
nieujemna określoność wynika z nieujemności wariancji dla zmiennej losowej. Dla
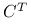 o wymiarach
o wymiarach 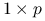 :
: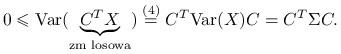
-
Jeżeli
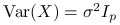 , a macierz
, a macierz 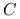 jest ortonormlna o wymiarach
jest ortonormlna o wymiarach 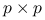 (
(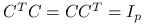 ), to:
), to: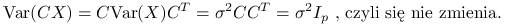
3.2. Redukcja Wymiaru danych
Wygodną postacią macierzy wariancji ![]() jest postać diagonalna. Wtedy korelacje pomiędzy różnymi elementami wektora losowego są zerowe.
jest postać diagonalna. Wtedy korelacje pomiędzy różnymi elementami wektora losowego są zerowe.
Problem 3.1
Jak przekształcić wektor losowy ![]() żeby zdiagonalizować
żeby zdiagonalizować ![]() ?
?
Twierdzenie 3.1
Rozkład spektralny macierzy symetrycznej ![]() .
Dla symetrycznej macierzy
.
Dla symetrycznej macierzy ![]() o wymiarze
o wymiarze ![]() istnieją:
istnieją:
-
ortonormalna (czyli
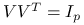 ) macierz kwadratowa
) macierz kwadratowa 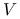 o wymiarze
o wymiarze 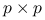 , oznaczmy
, oznaczmy ![V=[v_{1},\ldots,v_{p}]](wyklady/st2/mi/mi324.png) ;
; -
diagonalna macierz
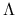 o wyrazach na przekątnych
o wyrazach na przekątnych  , że
, że
![]() to wektory własne macierzy
to wektory własne macierzy ![]() , a
, a ![]() to wartości własne, które dla macierzy symetrycznej są rzeczywiste. Wtedy:
to wartości własne, które dla macierzy symetrycznej są rzeczywiste. Wtedy:
Ponieważ macierz kowariancji ![]() wektora losowego
wektora losowego ![]() jest symetryczna, możemy zastosować do niej rozkład spektralny:
jest symetryczna, możemy zastosować do niej rozkład spektralny: ![]() .
Pomnóżmy wektor
.
Pomnóżmy wektor ![]() przez macierz
przez macierz ![]() :
: ![]() . Macierz kowariancji dla takiego wektora to:
. Macierz kowariancji dla takiego wektora to:
Ponieważ macierz ![]() jest nieujemnie określona, wszystkie jej wartości własne są nieujemne:
jest nieujemnie określona, wszystkie jej wartości własne są nieujemne: ![]() . Uporządkujmy wartości własne
. Uporządkujmy wartości własne ![]() i odpowiadające im wektory własne
i odpowiadające im wektory własne ![]() tak, żeby
tak, żeby ![]() . Oznaczmy dla tak ustawionych wektorów własnych:
. Oznaczmy dla tak ustawionych wektorów własnych:
3.2.1. Analiza składowych głównych – wersja populacyjna
Definicja 3.1
Mamy wektor losowy ![]() oraz macierz kowariancji
oraz macierz kowariancji ![]() .
.
Składowymi głównymi (principal components) nazywamy elementy wektora ![]() .
.
Kierunkami głównymi (rotations) nazywamy kolumny macierzy ![]() .
.
Stwierdzenie 3.2
Własności składowych głównych:
-
wsółrzędne wektora
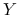 są nieskorelowane;
są nieskorelowane; -
wariancje poszczególnych
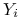 równe są
równe są 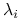 ;
; -
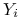 ustawione są od
ustawione są od 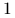 do
do 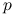 w kolejności nierosnących wariancji;
w kolejności nierosnących wariancji;
-
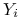 to kombinacje liniowe zmiennych losowych
to kombinacje liniowe zmiennych losowych 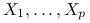 ;
;
Stwierdzenie 3.3
Kierunki główne to unormowane wektory, w kierunku których obserwujemy największą wariancję danych, będące wzajemnie do siebie prostopadłe:
-
jeżeli
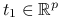 ,
, 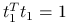

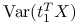 osiąga maksimum
osiąga maksimum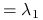 dla
dla 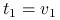 .
. -
jeżeli
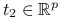 ,
, 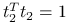 ,
, 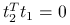

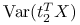 osiąga maksimum
osiąga maksimum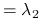 dla
dla 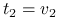 .
.
![]() jest bazą ortonormalną przestrzeni
jest bazą ortonormalną przestrzeni ![]() .
.
-
Zapiszmy
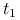 w tej bazie:
w tej bazie: 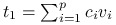 , gdzie
, gdzie 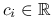 współczynniki. Z założeń wynika:
współczynniki. Z założeń wynika: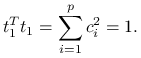
Zauważmy, że:
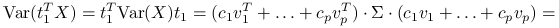
z własności wektorów własnych macierzy,
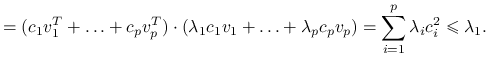
Jeżeli przyjmiemy
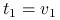 , czyli
, czyli 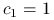 ,
, 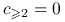 , otrzymujemy kombinację liniową o maksymalnej wariancji równej
, otrzymujemy kombinację liniową o maksymalnej wariancji równej 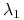 .
. -
Ponieważ
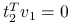 , możemy zapisać:
, możemy zapisać: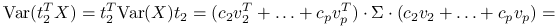
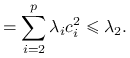
Analogicznie,
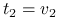 .
.
Stwierdzenie 3.4
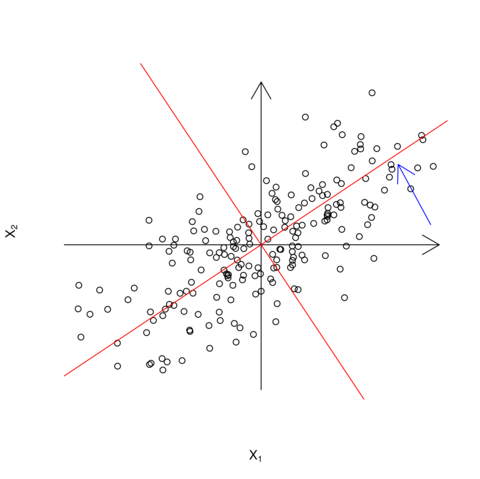
Ponieważ ![]() jest macierzą ortonormalną, możemy interpretować
jest macierzą ortonormalną, możemy interpretować ![]() jako współrzędne dla obróconego układu. Dla
jako współrzędne dla obróconego układu. Dla ![]() obrócone osie byłyby wyznaczone przez
obrócone osie byłyby wyznaczone przez ![]() i
i ![]() , przy czym
, przy czym ![]() byłby kierunkiem, w którym mamy największą zmienność danych, a
byłby kierunkiem, w którym mamy największą zmienność danych, a ![]() prostopadłym do niego (rysunek 3.1).
prostopadłym do niego (rysunek 3.1).
Definicja 3.2
Całkowity rozrzut danych dla wektora losowego ![]() to suma wariancji jego współrzędnych:
to suma wariancji jego współrzędnych: ![]() . Wariancje poszczególnych
. Wariancje poszczególnych ![]() można interpretować jako ilość informacji, jaką przechowuje dana zmienna: im większa wariancja, tym lepiej możemy różnicować obserwowane wielkości.
można interpretować jako ilość informacji, jaką przechowuje dana zmienna: im większa wariancja, tym lepiej możemy różnicować obserwowane wielkości.
Uwaga 3.1
Ślady macierzy ![]() i
i ![]() równają się sobie, czyli całkowite rozrzuty danych dla
równają się sobie, czyli całkowite rozrzuty danych dla ![]() i
i ![]() są równe:
są równe:
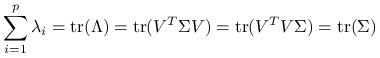 |
.
Istotnym parametrem diagnostycznym przy rozważaniu analizy składowych głównych jest:
czyli część całkowitego rozrzutu danych wyjaśniona przez ![]() pierwszych składowych głównych. Na jego podstawie dokonuje się redukcji wymiaru danych: z
pierwszych składowych głównych. Na jego podstawie dokonuje się redukcji wymiaru danych: z ![]() zmiennych zostaje utworzone
zmiennych zostaje utworzone ![]() kombinacji liniowych tych zmiennych, które wyjaśniają np.
kombinacji liniowych tych zmiennych, które wyjaśniają np. ![]() zmienności wyjściowych danych.
zmienności wyjściowych danych.
3.2.2. Analiza składowych głównych – wersja próbkowa
Podejście próbkowe do analizy danych różni się od populacyjnego tym, że w podejściu populacyjnym do analizy brana jest zmienna losowa, a w podejściu próbkowym jej realizacje. Dlatego teraz zamiast wektora zmiennych losowych ![]() będziemy rozpatrywać macierz jego
będziemy rozpatrywać macierz jego ![]() realizacji:
realizacji:
![X=\left(\begin{array}[]{ccc}X_{{11}}&\ldots&X_{{1p}}\\
X_{{21}}&\ldots&X_{{2p}}\\
&\ldots&\\
X_{{n1}}&\ldots&X_{{np}}\\
\end{array}\right)\quad=\quad\left(\begin{array}[]{c}X_{1}^{T}\\
X_{2}^{T}\\
\ldots\\
X_{n}^{T}\\
\end{array}\right).](wyklady/st2/mi/mi238.png) |
Do analizy potrzebna będzie macierz kowariancji próbkowej. Zdefiniujmy scentrowaną macierz ![]() jako:
jako:
![X_{c}=\left(\begin{array}[]{ccc}X_{{11}}-\overline{X}_{{.1}}&\ldots&X_{{1p}}-\overline{X}_{{.p}}\\
X_{{21}}-\overline{X}_{{.1}}&\ldots&X_{{2p}}-\overline{X}_{{.p}}\\
&\ldots&\\
X_{{n1}}-\overline{X}_{{.1}}&\ldots&X_{{np}}-\overline{X}_{{.p}}\\
\end{array}\right)\quad=\quad\left(\begin{array}[]{c}X_{{c1}}^{T}\\
X_{{c2}}^{T}\\
\ldots\\
X_{{cn}}^{T}\\
\end{array}\right),](wyklady/st2/mi/mi224.png) |
gdzie ![]() ,
, ![]() .
.
Zauważmy, że macierz kowariancji próbkowej możemy wyrazić za pomocą macierzy:
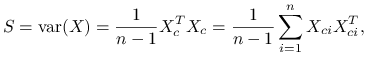 |
która jest nieobciążonym estymatorem macierzy kowariancji:
Macierz ![]() jest symetryczna i nieujemnie określona. Znajdźmy składowe główne dla podejścia próbkowego tą samą metodą jak dla podejścia populacyjnego:
jest symetryczna i nieujemnie określona. Znajdźmy składowe główne dla podejścia próbkowego tą samą metodą jak dla podejścia populacyjnego:
Wniosek 3.1
Składowe główne dla problemu próbkowego równe są wektorom ![]() , macierz kowariancji próbkowej dla
, macierz kowariancji próbkowej dla ![]() jest równa
jest równa ![]() .
.
3.2.3. Rozkład na wartości szczególne (Singular Value Decomposition)
Rozkład SVD posłuży nam do tańszej obliczeniowo konstrukcji składowych głównych w wersji próbkowej.
Twierdzenie 3.2
Rozkład na wartości szczególne
Dla dowolnej macierzy ![]()
![]() ,
, ![]()
![]() macierz ortonormalna
macierz ortonormalna ![]() oraz
oraz ![]() macierz ortonormalna
macierz ortonormalna ![]() takie, że
takie, że ![]() , gdzie
, gdzie ![]() jest macierzą diagonalną:
jest macierzą diagonalną:
gdzie ![]() jest rzędem macierzy
jest rzędem macierzy ![]() . Rozkład taki nazywamy szerokim rozkładem SVD, w odróżnieniu od wąskiego rozkładu SVD, w którym skracamy macierze do istotnych obliczeniowo:
. Rozkład taki nazywamy szerokim rozkładem SVD, w odróżnieniu od wąskiego rozkładu SVD, w którym skracamy macierze do istotnych obliczeniowo:
![\left(\begin{array}[]{c}\\
A\\
\\
\end{array}\right)_{{m\times n}}=\left(\begin{array}[]{c}\\
U\\
\\
\end{array}\right)_{{m\times m}}\left(\begin{array}[]{c}\\
\Sigma\\
\\
\end{array}\right)_{{m\times n}}\left(\begin{array}[]{c}\\
V\\
\\
\end{array}\right)_{{n\times n}}^{T}=](wyklady/st2/mi/mi322.png) |
![=\left(\begin{array}[]{ccc}&|&\\
\left(\begin{array}[]{c}U_{1}\\
\end{array}\right)_{{m\times k}}&|&\left(\begin{array}[]{c}U_{2}\\
\end{array}\right)_{{m\times(m-k)}}\\
&|&\\
\end{array}\right)\left(\begin{array}[]{cc}\Sigma^{{\prime}}&0\\
&\\
0&0\\
\end{array}\right)\left(\begin{array}[]{c}\left(\begin{array}[]{c}V_{1}\\
\end{array}\right)^{T}_{{n\times k}}\\
\\
\left(\begin{array}[]{c}V_{2}\\
\end{array}\right)^{T}_{{n\times(n-k)}}\\
\end{array}\right)=](wyklady/st2/mi/mi241.png) |
Zauważmy, że macierz ![]() jest symetryczna i nieujemnie określona:
jest symetryczna i nieujemnie określona:
Zatem, korzystając z rozkładu spektralnego dla ![]() otrzymujemy:
otrzymujemy:
| (3.1) |
gdzie założymy, że ![]() to nieujemne pierwiastki z
to nieujemne pierwiastki z ![]() :
:
Zauważmy, że ![]() jest podmacierzą
jest podmacierzą ![]() o niezerowych wyrazach na przekątnej:
o niezerowych wyrazach na przekątnej:
![V_{1}^{T}A^{T}AV_{1}=\left(\begin{array}[]{ccc}\sigma _{1}^{2}&&0\\
&\ldots&\\
0&&\sigma _{k}^{2}\\
\end{array}\right)](wyklady/st2/mi/mi228.png) |
Zdefiniujmy ![]() jako:
jako:
skąd otrzymujemy:
![U_{1}^{T}U_{1}=\left(\begin{array}[]{ccc}\sigma _{1}^{{-1}}&&0\\
&\ldots&\\
0&&\sigma _{k}^{{-1}}\\
\end{array}\right)\underbrace{V_{1}^{T}A^{T}AV_{1}}_{{\text{diag}(\sigma _{1}^{2},\ldots,\sigma _{k}^{2})}}\left(\begin{array}[]{ccc}\sigma _{1}^{{-1}}&&0\\
&\ldots&\\
0&&\sigma _{k}^{{-1}}\\
\end{array}\right)=I_{k}.](wyklady/st2/mi/mi249.png) |
Uzupełniamy dowolnie ![]() do ortonormalnej macierzy
do ortonormalnej macierzy ![]() :
: ![]() Wtedy:
Wtedy:
ponieważ ze wzoru (3.1) wynika, że ![]()
![]() takiego, że
takiego, że ![]() ,
, ![]() , a norma euklidesowa wektora jest równa zero wtedy i tylko wtedy gdy wektor jest równy zero, otrzymujemy:
, a norma euklidesowa wektora jest równa zero wtedy i tylko wtedy gdy wektor jest równy zero, otrzymujemy:
![=\left(\begin{array}[]{ccc}\text{diag}(\sigma _{1}^{{-1}},\ldots,\sigma _{k}^{{-1}})\underbrace{V_{1}^{T}A^{T}AV_{1}}_{{=\text{diag}(\sigma _{1}^{{2}},\ldots,\sigma _{k}^{{2}})}}&|&0\\
U_{2}^{T}U_{1}\text{ diag}(\sigma _{1},\ldots,\sigma _{k})&|&0\\
\end{array}\right)=](wyklady/st2/mi/mi373.png) |
Z równości ![]() , ponieważ
, ponieważ ![]() i
i ![]() są macierzami ortonormalnymi, wynika:
są macierzami ortonormalnymi, wynika:
Stwierdzenie 3.5
Wróćmy do analizy składowych głównych. Do scentrowanej macierzy danych ![]() o wymiarze
o wymiarze ![]() użyjmy wąskiego rozkładu SVD i oznaczmy:
użyjmy wąskiego rozkładu SVD i oznaczmy:
wtedy:
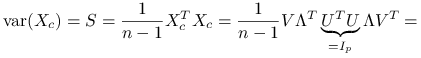 |
Wniosek 3.2
Zauważmy, że:
-
Składowe główne w wersji próbkowej przy użyciu rozkładu SVD:
![Y=X_{c}V=U\Lambda V^{T}V=U\Lambda=[\lambda _{1}U_{1},\ldots,\lambda _{p}U_{p}].](wyklady/st2/mi/mi285.png)
Obliczanie składowych głównych z tego wzoru jest tańsze obliczeniowo.
-
Widać związek pomiędzy rozkładem SVD dla
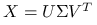 oraz rozkładem spektralnym dla
oraz rozkładem spektralnym dla 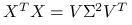 .
. -
Podobnie jest dla
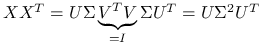 .
.
3.2.4. Kolejna zaleta analizy składowych głównych
Wróćmy do analizy składowych głównych w wersji populacyjnej.
Stwierdzenie 3.6
Przy założeniu, że wektor losowy ![]() jest scentrowany
jest scentrowany ![]() , możemy zapisać
, możemy zapisać ![]() . Korzystając z rozkładu spektralnego, oznaczmy
. Korzystając z rozkładu spektralnego, oznaczmy ![]() . Wtedy:
. Wtedy:
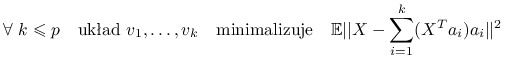 |
| wśród wszystkich układów ortonormalnych |
|
Czyli w sensie minimalizacji błędu średniokwadratowego najlepszym ![]() -wymiarowym przybliżeniem
-wymiarowym przybliżeniem ![]() jest rzut ortogonalny
jest rzut ortogonalny ![]() na
na ![]() pierwszych kierunków głównych.
pierwszych kierunków głównych.
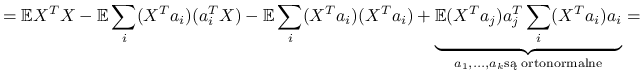 |
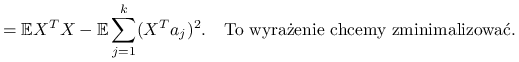 |
Czyli maksymalizujemy po ![]() :
:
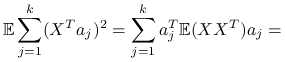 |
![=\sum _{{j=1}}^{k}a_{j}^{T}[\sum _{{i=1}}^{p}\lambda _{i}v_{i}v_{i}^{T}]a_{j}=\sum _{{j=1}}^{k}\sum _{{i=1}}^{p}\lambda _{i}(v_{i}^{T}a_{j})^{2}=\clubsuit](wyklady/st2/mi/mi248.png) |
Przyjrzyjmy się współczynnikom przy ![]() , są to kwadraty współczynników
, są to kwadraty współczynników ![]() w bazie ortonormalnej
w bazie ortonormalnej ![]() , więc sumują się do jedynki:
, więc sumują się do jedynki:
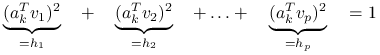 |
|||
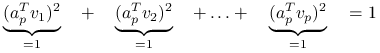 |
|||
Czyli otrzymujemy:
 |
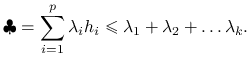 |
Jeśli podstawimy ![]() , otrzymujemy
, otrzymujemy ![]() , dla których osiągane jest wyliczone maksimum.
, dla których osiągane jest wyliczone maksimum.
3.3. Przykłady w programie R
Analiza składowych głównych:
-
dla danych Pima: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/pca.R
-
dla danych Iris i Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/rzutDanych.R