Zagadnienia
11. Metoda wzmacnienia klasyfikatorów (ang. Boosting)
11.1. Metoda wzmacnienia klasyfikatorów (ang. Boosting)
11.1.1. Wstęp
\blockBoosting jest ogólną metodą służącą zwiększeniu skuteczności dowolnego algorytmu uczenia. Idea Budowanie “mocnego i złożonego klasyfikatora” ze “słabych i prostych klasyfikatorów”. \pause\block
-
Leslie Valiant i Michael Kearns byli pierwszymi, którzy pokazali, że “słabe” algorytmy uczące, których skuteczność jest nawet niewiele lepsza niż losowe zgadywanie, mogą być wykorzystane do stworzenia dowolnie skutecznego “silnego” klasyfikatora.
-
Robert Schapire jako pierwszy przedstawił algorytm wzmacniania działający w czasie wielomianowym.
-
Yoav Freund zaproponował znacznie bardziej efektywny algorytm wzmacniania, który mimo tego, że był w pewnym sensie optymalny, miał pewne istotne w praktyce wady.
-
Pierwsze eksperymenty z tymi wczesnymi algorytmami wzmacniania zostały przeprowadzone przez zespół Drucker, Schapire, Simard i dotyczyły zadania OCR (ang. optical character recognition), w którym sieci neuronowe były użyte jako “proste” klasyfikatory.
-
Freund i Schapire przedstawili algorytm AdaBoost, który rozwiązał wiele praktycznych trudności wcześniejszych algorytmów wzmacniania.
11.1.2. AdaBoost - opis algorytmu
-
Algorytm na wejściu otrzymuje zbiór treningowy
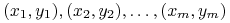 , gdzie każdy
, gdzie każdy 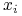 należy do pewnej
dziedziny problemu
należy do pewnej
dziedziny problemu  , natomiast każda etykieta (decyzja)
, natomiast każda etykieta (decyzja) 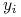 należy do pewnego
zbioru
należy do pewnego
zbioru 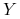 . Dla ułatwienia będziemy na razie zakładać, że
. Dla ułatwienia będziemy na razie zakładać, że 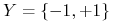 .
. -
AdaBoost (Adaptive Boosting) wywołuje wybrany “słaby” algorytm uczący w serii T iteracji. Zakładamy, że błąd uzyskiwanych klasyfikatorów na zbiorze treningowym jest mniejszy niż
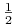 .
. -
Jedną z głównych idei algorytmu jest strojenie rozkładu (lub wag elementów) dla zbioru treningowego. Wagę
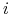 -tego elementu ze zbioru treningowego w iteracji
-tego elementu ze zbioru treningowego w iteracji 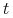 będziemy
oznaczali przez
będziemy
oznaczali przez 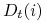 .
.
-
Początkowo wszystkie wagi są ustawione na równe wartości;
-
Po każdej iteracji, wagi elementów źle klasyfikowanych są zwiększane. Dzięki temu mamy możliwość skierowania uwagi “słabego” klasyfikatora na pewne elementy (trudne do wyuczenia) ze zbioru treningowego.
-
Zadaniem “słabego” algorytmu uczącego jest zbudowanie klasyfikatora (ang. hypothesis)
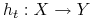 odpowiedniego dla aktualnego rozkładu
odpowiedniego dla aktualnego rozkładu 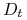 .
. -
Skuteczność takiego klasyfikatora jest mierzona przez jego błąd (z uwzględnieniem rozkładu
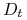 ):
):![\varepsilon _{t}=Pr_{{D_{t}}}[h_{t}(x_{i})\neq y_{i}]=\sum _{{i:h_{t}(i)\neq y_{i}}}D_{t}(i)](wyklady/syd/mi/mi849.png)
-
W praktyce “słaby” algorytm uczący może być algorytmem, który uwzględnia rozkład
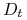 . Nie jest to
jednak konieczne. Kiedy algorytm nie pozwala na bezpośrednie uwzględnienie rozkładu
. Nie jest to
jednak konieczne. Kiedy algorytm nie pozwala na bezpośrednie uwzględnienie rozkładu 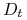 ,
losuje się (względem
,
losuje się (względem 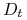 ) podzbiór zbioru treningowego, na którym następnie wywołuje się
algorytm uczący.
) podzbiór zbioru treningowego, na którym następnie wywołuje się
algorytm uczący. -
Kiedy AdaBoost dostaje klasyfikator
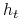 dobierany jest parametr
dobierany jest parametr 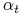 . Intuicyjnie
. Intuicyjnie 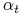 odpowiada za wagę jaką przykładamy do klasyfikatora
odpowiada za wagę jaką przykładamy do klasyfikatora 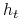 . Zauważmy, że
. Zauważmy, że 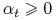 gdy
gdy
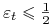 . Ponadto
. Ponadto 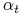 rośnie kiedy
rośnie kiedy 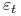 maleje.
maleje. -
Rozkład
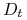 jest następnie zmieniany tak, aby zwiększyć (zmniejszyć) wagi elementów
zbioru treningowego, które są źle (dobrze) klasyfikowane przez
jest następnie zmieniany tak, aby zwiększyć (zmniejszyć) wagi elementów
zbioru treningowego, które są źle (dobrze) klasyfikowane przez 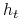 . Stąd wagi mają tendencję
do skupiania się na “trudnych” przykładach.
. Stąd wagi mają tendencję
do skupiania się na “trudnych” przykładach.
Dane: ![]() , gdzie
, gdzie ![]() ,
, ![]()
Inicjalizacja: ![]() dla
dla ![]()
for ![]() do:
do:
-
<+-> Wykorzystując “słaby” algorytm uczący zbuduj klasyfikator
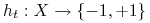
(uwzględniając rozkład
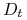 ).
). -
<+->
![\varepsilon _{t}=Pr_{{D_{t}}}[h_{t}(x_{i})\neq y_{i}]=\sum _{{i:h_{t}(i)\neq y_{i}}}D_{t}(i)](wyklady/syd/mi/mi860.png)
-
<+->
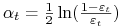
-
<+-> Uaktualnij wagi elementów zbioru treningowego:
\pause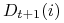
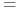
![\displaystyle\frac{D_{t}(i)}{Z_{t}}\times\left\{\begin{array}[]{l}e^{{-\alpha _{t}}}\ \textrm{ jeśli }h_{t}(x_{i})=y_{i}\\
e^{{\alpha _{t}}}\ \ \textrm{ jeśli }h_{t}(x_{i})\neq y_{i}\end{array}\right.](wyklady/syd/mi/mi870.png)
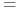
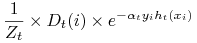
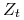 jest czynnikiem normalizującym (wybranym tak, aby
jest czynnikiem normalizującym (wybranym tak, aby 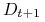 było rozkładem).
było rozkładem).
Wynikowy klasyfikator powstaje za pomocą ważonego głosowania klasyfikatorów ![]() , gdzie
, gdzie ![]() jest
wagą przypisaną klasyfikatorowi
jest
wagą przypisaną klasyfikatorowi ![]() .
.
| 1 | 2 | |||
| słabe klasyfikatory | ||||
| wagi | ||||
![]()




