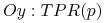Zagadnienia
3. Metody oceny klasyfikatorów
3.1. Metody oceny klasyfikatorów
3.1.1. Skuteczność predykcji
\blockBłąd klasyfikacji
gdzie:
-
Sukces: gdy obiekt jest prawidłowo klasyfikowany
-
Błąd: gdy obiekt jest źle klasyfikowany
-
Błąd klasyfikacji (lub odsetka błędów podczas klasyfikacji) powinien być wyznaczony na losowych i nieznanych danych.
-
Są dwa rodzaje błędu:
-
W “systemach uczących się”: minimalizujemy FP+FN lub miarę skuteczności (ang. Accuracy) (ACC):
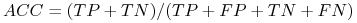
-
W marketingu: maksymalizujemy TP.
-
Podział zbioru danych na część treningową i testową;
-
Uczenie lub poszukiwanie modelu
-
Ocena klasyfikatora
-
Niektóre metody uczenia działają w dwóch etapach:
-
Etap 1: Buduje strukturę
-
Etap 2: Optymalizuje parametry
Uwaga: Nie używaj danych testowych do budowy klasyfikatorów!
-
Właściwa procedura powinna zawierać 3 zbiory: treningowe, walidacyjne i testowe
-
Dane walidacyjne używane są do optymalizacji parametrów
3.1.2. Przedział ufności miar ocen
-
Przykład:
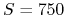 sukcesów w
sukcesów w 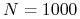 próbach
próbach-
Estymowana skuteczność:
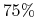
-
Jak bliska jest ta estymacja do prawdziwej skuteczności
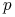 ?
? -
Odp: z
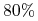 pewności możemy twierdzić, że
pewności możemy twierdzić, że ![p\in[73.2,76.7]](wyklady/syd/mi/mi158.png)
-
-
Inny przykład: S=75 i N=100
-
Estymowana skuteczność:
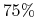 ;
; -
![p\in[69.1,80.1]](wyklady/syd/mi/mi142.png) z
z 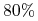 pewności.
pewności.
-
-
Rozpatrujemy rozkład Bernoulliego:
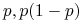
-
Oczekiwany odsetek sukcesu w
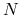 próbach:
próbach: 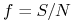
-
Wartość oczekiwana i wariancja dla
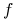 :
: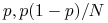
-
Dla dużych
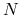 , zm.l.
, zm.l. 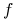 ma rozkład zbliżony do rozkładu normalnego;
ma rozkład zbliżony do rozkładu normalnego; -
![[–z\leq X\leq z]](wyklady/syd/mi/mi172.png) nazywamy przedziałem ufności na poziomie
nazywamy przedziałem ufności na poziomie 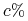 dla zm.l.
dla zm.l.  o zerowej wartości oczekiwanej wtw:
o zerowej wartości oczekiwanej wtw:![P[-z\leq X\leq z]=c](wyklady/syd/mi/mi162.png)
-
Dla rozkładu symetrycznego mamy:
![P[-z\leq X\leq z]=1-2P[X\geq z]](wyklady/syd/mi/mi152.png)
-
Wartość oczekiwana i wariancję dla
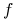 :
: 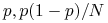
-
Normalizacja zm.
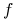 :
: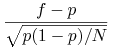
-
Mamy równanie na
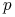 :
: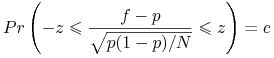
-
Rozwiązanie dla
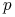 :
: ![p\in[p_{1},p_{2}]](wyklady/syd/mi/mi165.png) , gdzie
, gdzie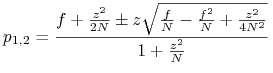
3.1.3. Metody walidacji danych
Ogólna zasada:
-
Im większy zbiór treningowy, tym lepszy jest klasyfikator
-
Im większy jest zbiór testowy, tym lepiej można aproksymować błąd klasyfikacji.
Praktyczna rada: Kiedy proces oceniania się zakończy, wszystkie dane mogą być wykorzystywane do skonstruowania ostatecznego klasyfikatora
-
Walidacja krzyżowa nie pozwala na wielokrotne testowanie tego samego obiektu
-
Krok 1: Podział zbioru danych na
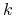 równych podzbiorów
równych podzbiorów -
Krok 2: Testowanie każdego podzbioru używając pozostałych jako zbiór treningowy
-
-
To się nazywa
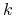 -CV =
-CV = 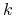 -fold cross-validation
-fold cross-validation -
Zwykle obiekty są przetasowane przed dokonaniem podziału.
-
Błędy wszystkich iteracji są uśrednione, aby otrzymać błąd globalny.
-
Standardowa metoda ocena klasyfikatorów: 10-krotna walidacja krzyżowa
-
Liczba 10 została wyznaczona w wyniku wielu doświadczeń.
-
Walidacja pozwala na zmniejszenie długości przedziału ufności
-
Jeszcze lepsza metoda oszacowania parametrów:
Walidacja z powtórzeniami!
-
Leave-one-out: przypadek szczególny walidacji krzyżowej Liczba grup = liczba przykładów
-
Dla
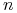 obiektów budujemy klasyfikator
obiektów budujemy klasyfikator 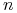 razy
razy -
Najlepiej ocenia klasyfikatora
-
Obliczeniowo kosztowna metoda (wyjątek:
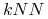 )
)
-
-
Bootstraping: próbkuje ze zwracaniem, żeby stworzyć różne zbiory treningowe i testowe
-
Próbkuje ze zwracaniem
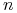 razy
razy -
Wybrane obiekty tworzą zbiór treningowy
-
Reszta – zbiór testowy.
-
3.1.4. Krzywy Lift i ROC
-
Miara “sensitivity” lub “true positive rate” (TPR)
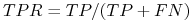
czasem nazywa się też “recall” lub “hit rate”.
-
Specificity (SPC) lub True Negative Rate
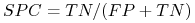
-
false positive rate (FPR):
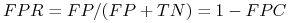
-
positive predictive value (PPV) lub precision:
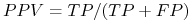
-
negative predictive value (NPV):
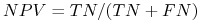
-
false discovery rate (FDR):
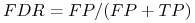
-
Matthew's correlation coefficient (MCC)
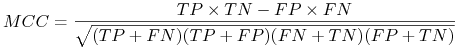
-
F1 score:
![F1=2TP/[(TP+FN)+(TP+FP)]](wyklady/syd/mi/mi137.png) lub
lub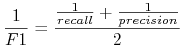
Funkcje
-
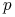 - parametr określający początek listy rankingowej
- parametr określający początek listy rankingowej -
CPH - (ang. Cumulative Percentage Hit)
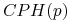 = część klasy docelowej znajdująca się wsród
= część klasy docelowej znajdująca się wsród 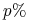 pierwszych obiektów z listy
rankingowej.
pierwszych obiektów z listy
rankingowej. -
zysk (ang. lift):
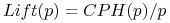
-
Trafienie lub true positive rate:
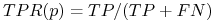
-
Odsetek fałszywych alarmów
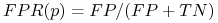
Wyróżnione krzywy
-
Gain chart:
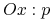
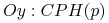
-
Lift chart:
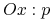
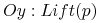
-
ROC (receiver operating characteristic):