Zagadnienia

8.1 Zagadnienie Mayera
8.2 Zagadnienie Bolzy

8. Istnienie sterowania optymalnego

W tym rozdziale zajmiemy się warunkiem wystarczającym istnienia sterowania optymalnego. W całym rozdziale zakładamy, że $\Omega=[-1,1]$ .

8.1. Zagadnienie Mayera

Rozważamy najpierw zagadnienie Mayera (M):

$\dot{x}=f(t,x,u)\,,\quad x(0)=x_{0}\,,\quad u\in{{\mathbb{U}}}_{m}$

(8.1)

z funkcjonałem kosztu

$\mathfrak{C}[u]=\mathfrak{g}\big({t_{1}},x({t_{1}})\big)\,,$

(8.2)

gdzie $x({t_{1}})=x({t_{1}};x_{0},{u(\,.\,)})$ oraz $f$ i $\mathfrak{g}$ są zadanymi funkcjami o wartościach w ${\mathbb{R}}^{n}$ i ${\mathbb{R}}^{1}$ , odpowiednio.

Sformułujemy twierdzenia mówiące o istnieniu sterowania optymalnego, tzn. takiego $u_{*}\in{\mathbb{U}}_{m}$ , że warunek (6.2) jest spełniony.

Analogia: Zagadnienie minimum rzeczywistej funkcji $h$ w obszarze $\mathbb{D}\in{\mathbb{R}}^{n}$ . Warunkiem wystarczającym (the sufficient condition) istnienia minimum jest:

$\mathbb{D}$ jest zbiorem zwartym (compact) i $h$ jest funkcją ciągłą.

Wprowadzamy następujące oznaczenie

Definicja 8.1

Dla $T>0$ zbiór $\Delta(T)\subset{\mathbb{U}}_{m}$ jest zbiorem sterowań, które prowadzą $x_{0}$ do ${\mathcal{T}}({t_{1}})$ w czasie ${t_{1}}$ , gdzie $0<{t_{1}}\leq T$ .

Podstawowymi założeniami są

Założenie 8.1

Funkcja

$f\,:\;[0,T]\times{\mathbb{R}}^{n}\times\Omega\,\to\,{\mathbb{R}}^{n}$

jest ciągła względem wszystkich zmiennych, różniczkowalna w sposób ciągły

względem $x\in{\mathbb{R}}^{n}$ oraz spełnia

$|f(t,x,v)|\leq\mathrm{const}.\,(1+|x|)\,,\qquad\forall\;(t,x,v)\in[0,T]\times{\mathbb{R}}^{n}\times\Omega\,.$

(8.3)

Założenie (8.3) może byc zastąpione innym, gwarantującym jednostajne oszacowanie odpowiedzi.

Założenie 8.2

Zbiór

$f(t,x,\Omega)=\Big\{ f(t,x,v)\,:\; v\in\Omega\Big\}$

(8.4)

jest zbiorem wypukłym (convex) dla wszystkich $t\in[0,T]$ , $x\in{\mathbb{R}}^{n}$ .

Założenie 8.2 gwarantuje domkniętość zbioru trajektorii — por. [14].

Przy powyższych założeniach można sformułować twierdzenie o istnieniu sterowania optymalnego dla zagadnienia Mayera:

Twierdzenie 8.1 (Istnienie sterowania optymalnego dla zagadnienia Mayera)

Niech będą spełnione następujące warunki dla $T>0$ :

funkcja $f$ spełnia założenia 8.1 oraz 8.2;
funkcja $\mathfrak{g}\,:\;[0,T]\times{\mathbb{R}}^{n}\,\to\,{\mathbb{R}}^{1}$ jest ciągła;
zbiór 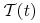${\mathcal{T}}(t)$ jest domknięty dla każdego $t\in[0,T]$
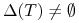
$\Delta(T)\not=\emptyset$

Wówczas istnieje optymalne sterowanie.

Szkic dowodu

[14], str. 89.

$\quad$

Ogólna idea dowodu istnienia sterowania optymalnego jest następująca: bada się (skomplikowane, nieliniowe) przekształcenie

$\mathfrak{C}\,:\quad{{\mathbb{U}}}_{m}\,\to\,{\mathbb{R}}^{1}$

i pokazuje następujące fakty

istnieje ciąg 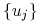$\{ u_{j}\}$ ,,minimalizujący” z odpowiedziami $\{ x_{j}(t)\}$ ,
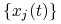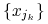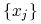pewien podciąg $\{ x_{{j_{k}}}\}$ ciągu $\{ x_{j}\}$ zbiega do pewnej granicy $x_{*}$ ,
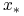istnieje 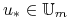$u_{*}\in{{\mathbb{U}}}_{m}$ , dla którego 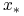$x_{*}$ jest odpowiedzią,
odpowiedź 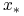$x_{*}$ spełnia wszystkie określone warunki.

Uwaga 8.1

W ogólnym przypadku nie wiemy czy $\{ u_{{j_{k}}}\}$ zbiega do $u_{*}$ . Dla zagadnień z liniową zależnością od sterowania można pokazać zbieżność $\{ u_{{j_{k}}}\}$ do $u_{*}$ .

∎

Przykład 8.1 ([14], str. 91)

Zagadnienie optymalnego sterowania dla

$\dot{x}=(x)^{2}\, u\,,\qquad x_{0}=1\,,$

$\mathfrak{g}({t_{1}},x({t_{1}}))=-x({t_{1}})\,.$

Cel nie jest ustalony, (zagadnienie swobodnego punktu końcowego), czas dotarcia $t_{1}>0$ jest ustalony.

Dla każdego $\varepsilon\in\,]\, 0,1\,[\,$ określamy sterowanie

$u_{{\varepsilon}}(t)=\left\{\begin{array}[]{ccc}1&\mathrm{dla}&t\in[0,1-\varepsilon]\\ 0&\mathrm{dla}&t>1-\varepsilon\,.\end{array}\right.$

Wówczas odpowiedź

$x_{{\varepsilon}}(t)=\left\{\begin{array}[]{ccc}\,\frac{1}{1-t}&\mathrm{dla}&t\in\,[\, 0,1-\varepsilon\,]\\ \frac{1}{\varepsilon}&\mathrm{dla}&t>1-\varepsilon\,.\end{array}\right.\,.$

Jeżeli ${t_{1}}>1$ , to $x_{{\varepsilon}}(t_{1})=\frac{1}{\varepsilon}$ . Zatem

$\mathfrak{g}({t_{1}},x({t_{1}}))=-\frac{1}{\varepsilon}\,.$

Nie ma więc sterowania optymalnego ( $\varepsilon$ może być dowolnie małe). To pokazuje, że oszacowanie (8.3) w założeniu 8.1, lub inne gwarantujące jednostajne oszacowanie, jest potrzebne.

Przykład 8.2 ([14], str. 92)

Zagadnienie optymalnego sterowania dla

$\dot{x}=u\,,\qquad x_{0}=1\,,$

$\mathfrak{g}({t_{1}},x({t_{1}}))=\big(x({t_{1}})-1\big)\mathrm{sign}\, x({t_{1}})\,.$

Infimium $\mathfrak{g}$ to $-1$ , ale nie jest nigdy osiągane. Funkcja $\mathfrak{g}$ nie jest ciągła!

Założenie o wypukłości 8.2 można odrzucić dla układu liniowego względem stanu

$\dot{x}=A(t)x+b(t,u)\,.$

Twierdzenie 8.2

Niech będą spełnione następujące warunki dla $T>0$ :

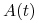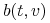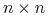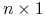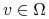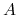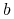$A(t)$ i $b(t,v)$ są macierzami $n\times n$ i $n\times 1$ , odpowiednio, dla $t\in[0,T]$ , $v\in\Omega$ oraz $A$ , $b$ są ciągłe;
funkcja $\mathfrak{g}\,:\;[0,T]\times{\mathbb{R}}^{n}\,\to\,{\mathbb{R}}^{1}$ jest ciągła;
zbiór 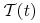${\mathcal{T}}(t)$ jest domknięty dla każdego $t\in[0,T]$
$\Delta(T)\not=\emptyset$

Wówczas istnieje optymalne sterowanie.

Dowód: [14], str. 92. $\;\clubsuit$

8.2. Zagadnienie Bolzy

Dla zagadnienia Bolzy (B) (lub zagadnienia Lagrange'a (L)) określamy

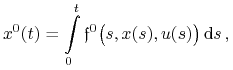$x^{0}(t)=\int\limits _{{0}}^{t}\mathfrak{f}^{0}\big(s,x(s),u(s)\big)\,\mathrm{d}s\,,$

wprowadzamy $(n+1)$ –wymiarowy wektor

$\mathbf{x}(t)=\big(x^{0}(t),x^{T}(t)\big)^{T}$

oraz

$\mathbf{f}(t,\mathbf{x})=\big(\mathfrak{f}^{0},f^{T}\big)^{T}(t,\mathbf{x})\,.$

W ten sposób sprowadzamy zagadnienie Bolzy (B) do zagadnienia Mayera (M) dla

$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},u)\,,$

(8.5)

z $\mathfrak{C}[u]=x^{0}({t_{1}})+\mathfrak{g}({t_{1}},x({t_{1}}))$ .

Twierdzenie o istnieniu sterowania optymalnego dla zagadnienia Bolzy wynika z twierdzenia 8.1. Założenie 8.2 jest zastąpione następującym:

Założenie 8.3

Zbiór

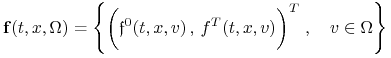$\mathbf{f}(t,x,\Omega)=\Bigg\{\bigg(\mathfrak{f}^{0}(t,x,v)\,,\, f^{T}(t,x,v)\bigg)^{T}\;,\quad v\in\Omega\Bigg\}$

(8.6)

jest zbiorem wypukłym w ${\mathbb{R}}^{{n+1}}$ dla wszystkich $0\leq t\leq T$ , $x\in{\mathbb{R}}^{n}$ .

Można sformułować twierdzenie o istnieniu sterowania optymalnego dla zagadnienia Bolzy:

Twierdzenie 8.3 (Istnienie sterowania optymalnego dla zagadnienia Bolzy)

Niech będą spełnione następujące warunki dla $T>0$ :

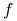funkcja $f$ spełnia założenie 8.1;
funkcje $\mathfrak{f}^{0}\,:\;[0,T]\times{\mathbb{R}}^{n}\times\Omega\,\to\,{\mathbb{R}}^{1}$ oraz $\mathfrak{g}\,:\;[0,T]\times{\mathbb{R}}^{n}\,\to\,{\mathbb{R}}^{1}$ są ciągłe;
jest spełniony założenie wypukłości 8.3;
zbiór 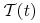${\mathcal{T}}(t)$ jest domknięty dla każdego $t\in[0,T]$
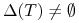
$\Delta(T)\not=\emptyset$

Wówczas istnieje optymalne sterowanie.

Dowód twierdzenia 8.3: [14], str. 94; [31], str. 92–95. $\;\clubsuit$

Założenie 8.3 o wypukłości $\mathbf{f}(t,x,\Omega)$ dotyczy geometrii związku pomiędzy $\mathfrak{f}^{0}$ i $f$ , a nie odnosi się do wypukłości $\mathfrak{f}^{0}$ i $f$ .

Przykład 8.3 ([31], str. 91)

$\dot{x}=|u|^{{\frac{1}{2}}}\;,\qquad{\mathfrak{C}}[u]=\int\limits _{0}^{{{{t_{1}}}}}|u(s)|^{{\frac{1}{2}}}x(s)\,\mathrm{d}\, s\,,$

$\mathbf{f}(t,x,\Omega)=\Big\{\big(|v|^{{\frac{1}{2}}}x\,,\,|v|^{{\frac{1}{2}}}\big)\;:\quad-1\leq v\leq 1\Big\}$

jest wypukły, choć $f$ nie jest funkcją wypukłą.

Przykład 8.4 ([31], str. 91)

$\dot{x}=u\,,\qquad{\mathfrak{C}}[u]=\int\limits _{0}^{{{{t_{1}}}}}\{ u(s)\}^{2}\,\mathrm{d}s\,,$

$\mathbf{f}(t,x,\Omega)=\Big\{\big(\big(v\big)^{2}\,,\, v\big)\;:\quad-1\leq v\leq 1\Big\}$

nie jest wypukły, choć $f$ jest liniowa, a ${\mathfrak{f}}^{0}$ — wypukła.

Założenie 8.1 jest istotne. W poniższym przykładzie nieliniowość względem zmiennej $x^{2}$ powoduje nieistnienie optymalnego sterowania.

Przykład 8.5 ([31], str. 83)

Niech $n=2$ , $m=1$ ,

$x=\left[\begin{array}[]{c}x^{1}\\ x^{2}\end{array}\right]\,,\quad\dot{x}^{1}=1\,,\quad\dot{x}^{2}=\big(x^{2}+1\big)^{2}u\,,\quad x_{0}=\left[\begin{array}[]{c}-2\\ \par \end{array}\right]$

$\mathfrak{C}[u]=\int\limits _{0}^{{t_{1}}}\mathfrak{f}^{0}(t,x,u)\,\mathrm{d}\, t$

$\mathfrak{f}^{0}(t,x,u)=\left\{\begin{array}[]{cc}\; 1&\qquad\mathrm{gdy}\; x^{2}<0\\ {\frac{1}{\big(x^{2}+1\big)^{2}}}&\qquad\mathrm{gdy}\; x^{2}\geq 0\end{array}\right.$

Cel jest ustalony $\mathcal{T}(t)\equiv\{ 0\}$ .

Mamy $x^{1}(t)=t-2$ , zatem musi być $t_{1}=2$ . Dla $u\equiv+1$ mamy $x^{1}(t)=t-2$ , $x^{2}(t)={\frac{t}{1-t}}$ , $0\leq t<1$ , więc nie jest to odpowiedź pomyślna. Dla $\alpha\in\,]\, 0,1\,[\,$ określmy

$u_{{\alpha}}(t)=\left\{\begin{array}[]{cc}\;\alpha&\qquad{\rm dla}\; 0\leq t\leq 1\\ -\alpha&\qquad{\rm dla}\; 1<t\leq 2\end{array}\right.$

Odpowiedzią (pomyślną) jest

$x^{1}_{{\alpha}}(t)=t-2\,,\quad x^{2}_{{\alpha}}(t)=\left\{\begin{array}[]{cc}\;{\frac{\alpha\, t}{1-\alpha\, t}}&\qquad{\rm dla}\; 0\leq t\leq 1\\ {\frac{\alpha\,(2-t)}{1-(2-t)\alpha}}&\qquad{\rm dla}\; 1\leq t\leq 2\end{array}\right.$

Rzeczywiście: na $0\leq t\leq 1$ :

$\frac{{\rm d}\, x^{2}}{\big(1+x^{2}\big)^{2}}=\alpha\,{\rm d}\, t\qquad\Rightarrow\qquad\Big[-\big(1+x^{2}\big)^{{-1}}\Big]_{{-2}}^{{x^{2}}}=\alpha\, t$

$\quad\Rightarrow\qquad-\frac{1}{1+x^{2}}+\frac{1}{1-2}=\alpha\, t\qquad\Rightarrow\qquad x^{2}=\frac{\alpha\, t}{1-\alpha\, t}$

Na $1<t\leq 2$ : warunek początkowy dla $t=1$ ma postać $x^{2}=\frac{\alpha}{1-\alpha}$

$\Big[-\big(1+x^{2}\big)^{{-1}}\Big]_{{\frac{\alpha}{1-\alpha}}}^{{x^{2}}}=-\alpha\, t+\alpha\qquad\Rightarrow$

$-\frac{1}{1+x^{2}}+\frac{1}{1+\frac{\alpha}{1-\alpha}}=-\alpha\,(t-1)\qquad\Rightarrow\qquad-\frac{1}{1+x^{2}}=2\alpha-1-\alpha t$

$\Rightarrow\qquad x^{2}=\frac{-\alpha\,(t-2)}{1+\alpha\,(t-2)}$

$\mathfrak{C}[u_{{\alpha}}]=\int\limits _{0}^{{t_{1}}}\frac{1}{\big(1+x^{2}\big)^{2}}\,\mathrm{d}t=\int\limits _{0}^{1}\frac{1}{\Big(1+\frac{\alpha\, t}{1-\alpha\, t}\Big)^{2}}\,\mathrm{d}t+\int\limits _{1}^{2}\frac{1}{\Big(1+\frac{\alpha\,(2-t)}{1-\alpha\,(2-t)}\Big)^{2}}\,\mathrm{d}t=$

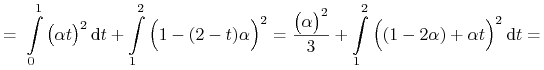$=\;\int\limits _{0}^{1}\big(\alpha t\big)^{2}\,\mathrm{d}t+\int\limits _{1}^{2}\Big(1-(2-t)\alpha\Big)^{2}=\frac{\big(\alpha\big)^{2}}{3}+\int\limits _{1}^{2}\Big((1-2\alpha)+\alpha t\Big)^{2}\,\mathrm{d}t=$

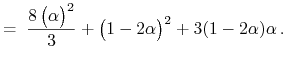$=\;\frac{8\,\big(\alpha\big)^{2}}{3}+\big(1-2\alpha\big)^{2}+3(1-2\alpha)\alpha\,.$

Gdy $\alpha\uparrow 1$ funkcja $x^{2}_{{\alpha}}(t)$ zbiega do pewnej funkcji osobliwej w $t=1$ .

Ponadto $\mathfrak{C}[u_{{\alpha}}]\to\frac{2}{3}$ gdy $\alpha\uparrow 1$ . Zatem optymalne sterowanie $u_{*}$ powinno spełniać warunek

$\mathfrak{C}[u_{*}]\leq\frac{2}{3}\,.$

Pokażemy, że każde pomyślne sterowanie daje koszt $\;>\frac{2}{3}\,$ .

Dla pomyślnego sterowania mamy $x^{2}(0)=x^{2}(2)=0$ oraz bezpośrednio z równania, dla $-1\leq u(t)\leq 1$ otrzymujemy

$-\big(x^{2}(t)+1\big)^{2}\leq\dot{x}^{2}(t)\leq\big(x^{2}(t)+1\big)^{2}\,.$

Stąd, z nierówności po prawej stronie (całkując od $0$ do $t<1$ ),

$-\frac{1}{x^{2}(t)+1}+1\leq t\,,\qquad{\mathrm{czyli}}\qquad\frac{1}{x^{2}(t)+1}\geq 1-t\,,$

dla $0\leq t<1\,$ .

Z nierówności po lewej stronie (całkując od $t\geq 1$ do $2$ ),

$-2+t\leq-1+\frac{1}{x^{2}+1}\,,\qquad{\rm czyli}\quad t-1\leq\frac{1}{x^{2}+1}\,,$

dla $1\leq t\leq 2\,$ .

Ale pomyślna odpowiedź musi być ograniczona (jako funkcja ciągła na zbiorze zwartym), więc pierwsza nierówność jest ostra. Zatem

$\mathfrak{C}[u]>\int\limits _{0}^{1}(1-t)^{2}\,{\rm d}t+\int\limits _{1}^{2}(t-1)^{2}\,{\rm d}t=\frac{2}{3}\,.$

Wniosek: nie istnieje optymalne sterowanie!

Następujący przykład pokazuje, ze nawet dla ograniczonych odpowiedzi, zależność od sterowania $u$ może powodować nieistnienie optymalnego sterowania. Potrzebne jest więc dodatkowe założenie, n.p. o wypukłości 8.3.

Przykład 8.6 ([31], str. 85)

Niech $n=3$ , $m=1$ ,

$x=\left[\begin{array}[]{c}x^{1}\\ x^{2}\\ x^{3}\end{array}\right]\,,\qquad{\dot{x}}=\left[\begin{array}[]{c}\sin(2\,\pi\, u)\\ \cos(2\,\pi\, u)\\ -1\end{array}\right]\,,\qquad x_{0}=\left[\begin{array}[]{c}0\\ 0\\ 1\end{array}\right]\,.$

$\mathfrak{C}[u]=\int\limits _{0}^{{t_{1}}}\Big(\big(x^{1}(t)\big)^{2}+\big(x^{2}(t)\big)^{2}\big)\,\mathrm{d}t\,.$

Cel jest ustalony $\mathcal{T}(t)\equiv 0$ .

Mamy $x^{3}(t)=1-t$ , zatem musi być $t_{1}=1$

Każda odpowiedź spełnia $|\dot{x}|\leq c$ , a zatem $|x(t)|\leq|x_{0}|+ct\leq c+1$ dla $0\leq t\leq 1$ .

Skonstruujemy ciąg sterowań $\{ u_{j}\} _{{j\in{\mathbb{N}}}}$ , t.ż. $\mathfrak{C}[u_{j}]\to 0$ dla $j\to\infty$ .

Ponieważ zawsze $\mathfrak{C}[u]\geq 0$ , każde sterowanie optymalne $u_{*}$ musiałoby spełniać $\mathfrak{C}[u_{*}]=0$

To prowadzi do sprzeczności, gdyż wtedy

$x^{1}_{*}(t)=x^{2}_{*}(t)=0\,,\qquad{\rm p.w.}\,,$

a zatem $\dot{x}^{1}_{*}(t)=\dot{x}^{2}_{*}(t)=0$ , co jest niemożliwe, gdyż

$\dot{x}^{1}_{*}(t)=\sin(2\,\pi\, u_{*}(t))\,,\qquad\dot{x}^{2}_{*}(t)=\cos(2\,\pi\, u_{*}(t))\,.$

W.w. ciąg sterowań ma postać $u_{j}(t)=jt-[jt]$ , $j=1,2,\ldots$ .

Wówczas

$\sin\Big(2\,\pi\, u_{j}(t)\Big)=\sin(2\,\pi\, jt)\,,\qquad\cos\Big(2\,\pi\, u_{j}(t)\Big)=\cos(2\,\pi\, jt)\,.$

Odpowiedź ma postać

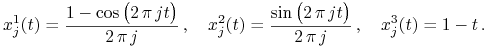$x^{1}_{j}(t)=\frac{1-\cos\big(2\,\pi\, jt\big)}{2\,\pi\, j}\,,\quad x^{2}_{j}(t)=\frac{\sin\big(2\,\pi\, jt\big)}{2\,\pi\, j}\,,\quad x^{3}_{j}(t)=1-t\,.$

Mamy więc

$\mathfrak{C}[u_{j}]=\int\limits _{0}^{1}{\frac{2\,\big(1-\cos(2\,\pi\, jt)\big)\,\mathrm{d}\, t}{(2\,\pi\, j)^{2}}}=\frac{1}{2\,\pi^{2}\, j^{2}}\,,$

czyli rzeczywiście $\mathfrak{C}[u_{j}]\to 0$ dla $j\to\infty$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Teoria sterowania

Zagadnienia

8. Istnienie sterowania optymalnego

8.1. Zagadnienie Mayera

Definicja 8.1

Założenie 8.1

Założenie 8.2

Twierdzenie 8.1 (Istnienie sterowania optymalnego dla zagadnienia Mayera)

Szkic dowodu

Uwaga 8.1

Przykład 8.1 ([14], str. 91)

Przykład 8.2 ([14], str. 92)

Twierdzenie 8.2

8.2. Zagadnienie Bolzy

Założenie 8.3

Twierdzenie 8.3 (Istnienie sterowania optymalnego dla zagadnienia Bolzy)

Przykład 8.3 ([31], str. 91)

Przykład 8.4 ([31], str. 91)

Przykład 8.5 ([31], str. 83)

Przykład 8.6 ([31], str. 85)