Zagadnienia

11.1 Twierdzenie Liouville'a
11.2 Równania Lagrange'a i Hamiltona. Potoki geodezyjne

11. O gładkich miarach niezmienniczych

11.1. Twierdzenie Liouville'a

To twierdzenie jest znane z kursu Równań Rożniczkowych Zwyczajnych.

Rozważmy równanie różniczkowe $\dot{x}=F(x)$ (gdzie $F$ jest funkcją klasy $C^{1}$ na gładkiej zwartej rozmaitości, albo (dla uproszczenia) w $R^{m}$ . Na rozmaitości zwartej każde rozwiązanie takiego równania można przedłużyć na całą prostą; w $R^{m}$ tak nie musi być, ale - jest tak na pewno na przykład wtedy gdy funkcja $F$ jest ograniczona lub gdy mamy równanie hamiltonowskie i poziomice hamiltonianu są zwarte.

Niech $\varphi^{t}$ będzie potokiem tego pola wektorowego, zatem $\frac{d}{dt}\varphi^{t}(x)_{{|t=0}}=F(x)$ . Dla $t$ bliskich zeru mamy więc

$\varphi^{t}(x)=x+F(x)\cdot t+O(t^{2})$

(11.1)

Niech $D$ będzie obszarem; oznaczmy $D(t)={\rm vol}(\varphi^{t}(D)$ .

Twierdzenie 11.1

Jeżeli ${\rm div}F\equiv 0$ to funkcja $D(t)$ jest stała, czyli potok pola zachowuje objętość w przestrzeni fazowej.

Sprawdzimy że

$\frac{d}{dt}D(t)_{{|t=0}}=\int _{D}{\rm div}Fdx$

Istotnie, mamy policzyć

$\frac{d}{dt}\int _{D}|{\rm Jac}\varphi^{t}(x)|dx=\frac{d}{dt}\int _{D}{\rm Jac}\varphi^{t}(x)dx_{{|t=0}}$

Oprócz 11.1 mamy, dla $t$ bliskich zeru:

$D_{x}\varphi^{t}(x)=I+t\frac{\partial F}{\partial x}+O(t^{2})$

Ten drugi wzór wyraża twierdzenie mówiace iż $D_{x}\varphi^{t}(x)$ - funkcja zmiennej $t$ o wartościach macierzowych, spełnia równanie różniczkowe liniowe $\dot{Y}=\frac{\partial F}{\partial x}(\varphi^{t}(x))Y$ z warunkiem początkowym $Y(0)=I$ .

Jeśli- licząc wyznacznik macierzy $D_{x}\varphi^{t}(x)$ interesujemy się tylko jego pochodną względem $t$ , to widzimy że przy liczeniu wyznacznika $I+t\frac{\partial F}{\partial x}+O(t^{2})$ musimy wziąć tylko te wyrazy które zawierają $t$ w pierwszej potędze. Po zsumowaniu-mamy

$\frac{d}{dt}{\rm Jac}\varphi^{t}(x)_{{|t=0}}=\frac{\partial F_{1}}{\partial x_{1}}+\frac{\partial F_{2}}{\partial x_{2}}+\dots+\frac{\partial F_{m}}{\partial x_{m}}={\rm div}F(x)$

(11.2)

Zauważamy dalej, że

$\frac{d}{dt}D(t)_{{|t=t_{0}}}=\frac{d}{ds}D(t_{0}+s)_{{|s=0}}=\frac{d}{ds}{\rm vol}\varphi^{{t_{0}+s}}(D)_{{|s=0}}=\frac{d}{ds}_{{|s=0}}{\rm vol}\varphi^{s}(\varphi^{{t_{0}}}(D))$

ZAtem, z udowodnionej już części, zastosowanej dla $\varphi^{{t_{0}}}(D)$ wynika teza.

Latwo widać że warunek $\div F=0$ jest też konieczny (szczegóły zostawiamy jako ćwiczenie)

∎

Uwaga 11.1

W podobny sposób można sprawdzić że jeśli $\rho>0$ jest funkcją klasy $C^{1}$ i ${\rm div}(\rho\cdot F)=0$ to potok pola wyznaczonego przez $F$ zachowuje miarę z gęstością $\rho$ względem miary Lebesgue'a.

Wniosek 11.1

Rozważmy pole hamiltonowskie w $R^{{2m}}$ ; $H$ jest funkcją klasy $C^{2}$ , układ równań ma postać

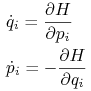$\begin{aligned}\displaystyle&\displaystyle\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}\\ \displaystyle&\displaystyle\dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}\end{aligned}$

(11.3)

Zatem $F=\left(\frac{\partial H}{\partial p_{1}},\dots,\frac{\partial H}{\partial p_{m}},-\frac{\partial H}{\partial q_{1}},\dots-\frac{\partial H}{\partial q_{m}}\right)$ .

Ponieważ ${\rm div}F=0$ , otrzymujemy ważny wniosek: Potok pola hamiltonowskiegoz achowuje objętość w przestrzeni fazowej.

Potok hamiltonowski ma calkę pierwszą: jest nią funkcja Hamiltona $H$ . Zatem przestrzeń fazowa rozpada się na niezmiennicze powierzchnie stałej energii. Mamy

Twierdzenie 11.2

Jeśli dla układu hamiltonowskiego powierzchnia stałej energii $\Sigma=\{ H=c\}$ spełnia ${\rm grad}H\neq 0$ w każdym punkcie tej powierzchni, to miara na $\Sigma$ określona wzorem

$\mu(A)=\int _{A}\frac{d\sigma}{||{\rm grad}H||}$

jest niezmiennicza względem potoku pola z hamiltonianem $H$ . $\sigma$ oznacza tutaj standardową miarę powierzchniową na powierzchni $\Sigma$ .

Skoro ${\rm grad}H\neq 0$ na powierzchni $\Sigma$ , możemy założyć (ograniczając się do pewnego otwartego podzbioru $\Sigma$ ) że $\frac{\partial H}{\partial p_{m}}\neq 0$ na $\Sigma$ . W tekim razie, $p_{m}$ daje się (lokalnie) wyznaczyć jako funkcja pozostałych zmiennych; $p_{m}=F(q_{1},\dots,q_{m},p_{1},\dots p_{{m-1}})=F(q,p^{{\prime}})$ . Miara powierzchniowa $\sigma$ na $\Sigma$ może być więc wyliczona według formuły:

$\sigma(A)=\int _{{\tilde{A}}}\sqrt{1+||{\rm grad}F||^{2}}$

$\tilde{A}$ jest mierzalnym zbiorem $\mathbb{R}^{{2m-1}}$ , $A=\{(x,F(x)),x\in\tilde{A}\}$ jest odpowiadającym mu zbiorem na wykresie. Bezpośrednim rachunkiem wyliczamy że

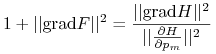$1+||{\rm grad}F||^{2}=\frac{||{\rm grad}H||^{2}}{||\frac{\partial H}{\partial p_{m}}||^{2}}$

(pominęliśmy w tym napisie argumenty funkcji) Zatem

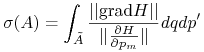$\sigma(A)=\int _{{\tilde{A}}}\frac{||{\rm grad}H||}{||\frac{\partial H}{\partial p_{m}}||}dqdp^{{\prime}}$

zaś

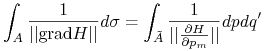$\int _{A}\frac{1}{||{\rm grad}H||}d\sigma=\int _{{\tilde{A}}}\frac{1}{||\frac{\partial H}{\partial p_{m}}||}dpdq^{{\prime}}$

Przekształcenie

$\mathbb{R}^{{2m-1}}\ni(q,p^{{\prime}})=(q_{1},\dots q_{m},p_{1},\dots,p_{{m-1}})\mapsto(q_{1},\dots q_{m},p_{1},\dots,p_{{m-1}},F(q,p^{{\prime}}))\in\mathbb{R}^{{2m}}$

jest parametryzacją rozmaitości $\Sigma$ , zaś miara $\frac{1}{||{\rm grad}H||}d\sigma$ na $\Sigma$ jest- jak sprawdziliśmy- obrazem miary ${||\frac{\partial H}{\partial p_{m}}||}dpdq^{{\prime}}$ w przestrzeni parametrów. Aby sprawdzić że potok wyjściowego pola 11.3 zachowuje miarę $\frac{1}{||{\rm grad}H||}d\sigma$ , możemy więc sprawdzić, rownoważnie, że potok pola przeniesionego parametryzacją do $\mathbb{R}^{{2m-1}}$ zachowuje miarę ${||\frac{\partial H}{\partial p_{m}}||}dpdq^{{\prime}}$ . Jest to miara z gęstością $rho={||\frac{\partial H}{\partial p_{m}}||}$ względem miary Lebesgue'a. Aby sprawdzić że jest ona zachowana, skorzystamy z Uwagi 11.1).

Równania we współrzędnych $(q,p^{{\prime}})$ wyglądają oczywiście:

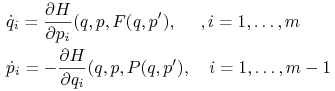$\begin{aligned}\displaystyle&\displaystyle\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}(q,p,F(q,p^{{\prime}}),~~~~,i=1,\dots,m\\ \displaystyle&\displaystyle\dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}(q,p,P(q,p^{{\prime}}),~~~i=1,\dots,m-1\end{aligned}$

(11.4)

Oznaczając przez $X$ funkcję wektorową (w $\mathbb{R}^{{2m-1}}$ ) po prawej stronie równania mamy więc sprawdzić że ${\rm div}(\rho\cdot X)=0$ . Liczymy

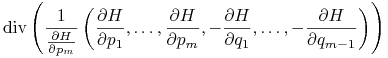${\rm div}\left(\frac{1}{\frac{\partial H}{\partial p_{m}}}\left(\frac{\partial H}{\partial p_{1}},\dots,\frac{\partial H}{\partial p_{m}},-\frac{\partial H}{\partial q_{1}},\dots,-\frac{\partial H}{\partial q_{{m-1}}}\right)\right)$

(znowu pominęliśmy w zapisie argumenty występujących tu funkcji). Poszczególne składniki (występujace we wzorze na dywergencję) wypiszmy z uwzględnieniem argumentów: Pierwszy składnik to:

$\frac{\partial}{\partial q_{1}}\left[\frac{\frac{\partial H}{\partial p_{1}}(q,p^{{\prime}},F(q,p^{{\prime}})}{\frac{\partial H}{\partial p_{m}}(q,p^{{\prime}},F(q,p^{{\prime}})}\right]=\frac{\partial}{\partial q_{1}}\left(-\frac{\partial F}{\partial p_{1}}\right)$

Stąd już łatwo widać że suma składników jest równa zero, co kończy dowód.

∎

11.2. Równania Lagrange'a i Hamiltona. Potoki geodezyjne

W mechanice klasycznej równania ruchu punktu materialnego w polu sił z potencjałem $V$ są opisywane przez równania Eulera-Lagrange'a: Niech $M$ będzie rozmaitością riemannowską (przestrzenią konfiguracji), $TM$ -wiązką styczną (przestrzenią fazową). Funkcja Lagrange'a

$L:TM\to\mathbb{R}:L(x,v)=\frac{1}{2}<v,v>-V(x)=K-V$

(11.5)

jest rózniczkowalną funkcją opisującą ruch przez równanie różniczkowe pierwszego rzędu w $TM$ :

$\frac{d}{dt}\frac{\partial L}{\partial v}=\frac{\partial L}{\partial x}$

$K(v)=\frac{1}{2}<v,v>$ jest energią kinetyczną. Rozwiązanie jest to zatem funkcja $t\mapsto(x(t),v(t))\in TM$ . Tutaj iloczyn skalarny $<v,v>$ odpowiadający strukturze Riemannowskiej na $M$ (w szczególności, zależy od od punktu $x$ , gdzie $v\in T_{x}M$ ).

Stwierdzenie 11.1

Równanie Lagrange'a ma całkę pierwszą; jest nią całkowita energia $H(x,v)=\frac{1}{2}<v,v>+V(x)$

Użyjemy lokalnych współrzędnych; w tych współrzędnych możemy zapisać iloczyn skalarny w przestrzeni stycznej prz pomocy macierzy symetrycznej $g^{{ij}}$ . Zatem

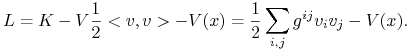$L=K-V\frac{1}{2}<v,v>-V(x)=\frac{1}{2}\sum _{{i,j}}g^{{ij}}v_{i}v_{j}-V(x).$

Oznaczając przez $<.,.>_{e}$ zwykły iloczyn skalarny w przestrzenie euklidesowej, możemy napisać

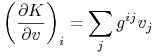$\left(\frac{\partial K}{\partial v}\right)_{i}=\sum _{j}g^{{ij}}v_{j}$

Zatem:

$<\frac{\partial K}{\partial v},v>_{e}=2K$

zaś

$<\frac{\partial L}{\partial v},v>_{e}-L=<\frac{\partial K}{\partial v},v>_{e}-L=2K-K+V=K+V=H$

Dzięki tej formule możemy łatwo policzyć pochodną funkcji $H$ wzdłuż rozwiązania:

$\frac{d}{dt}H(x(t),v(t))=\frac{d}{dt}<\frac{\partial L}{\partial v},v>_{e}=<\frac{d}{dt}\frac{\partial L}{\partial v},v>_{e}+<\frac{\partial L}{\partial v},\frac{dv}{dt}>_{e}-<\frac{\partial L}{\partial x},\dot{x}>_{e}-<\frac{\partial L}{\partial v},\dot{v}>_{e}$

Z równania Eulera-Lagrange'a ( i z faktu że $\dot{x}=v$ ) wynika że ta suma jest równa zero.

∎

Uwaga 11.2

Jeśli rozmaitość $M$ jest zwarta, to każda poziomica funkcji $H$ jest zwartą podrozmaitością $TM$ . Z twierdzenia o przedłużaniu trajektorii wynika że wówczas każde rozwiązanie równania Eulera- Legrange'a można przedłużyć do nieskończoności, zatem potok pola jest określony dla wszystkich $t\in\mathbb{R}$ .

Szczególnym przypadkiem jest potok geodezyjny, opisujący ruch swobodny na rozmaitości $M$ (w przestrzeni konfiguracji z ”więzami”):

Definicja 11.1

Potokiem geodezyjnym na rozmaitości Riemannowskiej $M$ nazywamy potok pola zadanego przez równanie Eulera-Lagrange'a z funkcją Lagrange'a równą

$L(x,v)=\frac{1}{2}<v,v>$

Ponieważ potok ten zachowuje dlugość wektora stycznego $v(t)$ , więc potok można rozpatrywać na podrozmaitościach stałej energii; w tym przypadku- są to podrozmaitości $TM$ odpowiadające ustalonej długości wektorów stycznych.

Następujące twierdzenie, wynikające z zasady wariacyjnej, uzasadnia nazwę:

Twierdzenie 11.3

Jeśli $x(t),v(t)$ jest trajektorią (rozwiązaniem) równania Eulera-Lagrange'a dla $V=0$ , to rzut trajektorii na $M$ jest geodezyjną w $M$ .

Potok geodezyjny ma naturalną gładką miarę niezmienniczą. Wyliczymy ją, przechodząc do odpowiedniego równania Hamiltonowskiego. Opiszemy to przejście (standardowe w mechanice klasycznej).

W przestrzeni stycznej $T_{x}M$ jest struktura iloczynu skalarnego, która pozwala utożsamic przestrzeń styczną z przestrzenią kostyczną $T^{*}_{x}M$ w oczywisty sposób: wektor $v$ jest utożsamiany z funkcjonałem liniowym $w\mapsto<v,w>$ . Używając lokalnych współrzędnych możemy zapisać $v=(v_{i})$ , wówczas

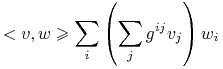$<v,w\geq\sum _{i}\left(\sum _{j}g^{{ij}}v_{j}\right)w_{i}$

( $g^{{ij}}$ zależa oczywiście od punktu $x$ ). Zatem wektorowi $v$ odpowiada element $T^{*}_{x}M$ , który w lokalnej bazie $dx_{i}$ ma współrzędne $\sum _{j}g^{{ij}}v_{j}$ . Ta ostatnia suma jest równa, jak wiemy, $\left(\frac{\partial K}{\partial v}\right)_{i}$ . W ten sposób określiliśmy przekształcenie Legendre'a $\mathcal{L}$ prowadzące z wiązki stycznej $TM$ do wiązki kostycznej $T^{*}M$ . Możemy więc użyć współrzędnych lokalnych $q_{i}$ w $M$ i odpowiadającym ich w opisany sposób współrzędnych $p_{i}$ w przestrzeni $T^{*}_{x}M$ do utworzenia lokalnych współrzędnych w $T^{*}M$ .

Załóżmy że trajektoria $(q(t),v(t))$ spełnia równanie Eulera-Lagrange'a. Sprawdźmy jakie równanie spełnia odpowiadająca trajektoria w przestrzeni $TM$ : $(q(t),p(t))$ .

Stwierdzenie 11.2

Jeśli $(q(t),v(t))$ spełnia równanie Eulera-Lagrange'a z funkcja Lagrange'a 11.5, to $(q(t),p(t))$ , uzyskane przez zamianę zmiennych transformatą Legendre'a- spełnia równanie Hamiltona 11.3 z funkcją $H$ równą całkowitej energii.

W nowych współrzędnych $(q,p)$ funkcja całkowitej energii $H$ ma postać $H(q,p)=\frac{1}{2}\sum _{{i,j}}g_{{ij}}p_{i}p_{j}+V(q)$ gdzie $g_{{ij}}$ jest macierzą odwrotną do $g^{{ij}}$ .

Mamy

$\dot{q}^{i}=v^{i}=\sum g_{{ij}}p_{j}=\frac{\partial H}{\partial p_{i}}$

Stąd pierwsze równanie Hamiltonowskie. Pozostaje wyznaczyć $\dot{p}$ . Skoro $p=\frac{\partial K}{\partial v}=\frac{\partial L}{\partial v}$ , to z równania Eulera-Lagrange'a wynika że $\dot{p}=\frac{\partial L}{\partial q}$ . Funkcję energii $H$ możemy zapisać inaczej jako $\frac{1}{2}<v,v>+V=<v,p>_{e}-L$ . Stąd $\frac{\partial H}{\partial q}=-\frac{\partial L}{\partial q}$ . uzupelnic

∎

Potok pola hamiltonowskiego otrzymanego z pola Lagrange'a przez opisaną zamianę zmiennych zachowuje- jak juz sprawdziliśmy- naturalna miarę, którą w lokalnych współrzędnych $(p,q)$ można zapisać $dpdq$ . Wracając do współrzędnych na rozmaitości $TM$ otrzymujemy miarę niezmienniczą na $TM$ ; jej postać wyliczamy poniżej.

Macierz iloczynu skalarnego $(g^{i}j)$ możemy zdiagonalizować, znajdując macierz $C=C_{q}$ (zależną oczywiscie od polozenia) taką że $C^{T}GC=I$ Jesli zmienimy wspolrzedne w $T^{*}M$ kładąc $p^{{\prime}}=C_{q}(p)$ , $q^{{\prime}}=q$ , to otrzymamy

$dqdp=dq^{{\prime}}dp^{{\prime}}({\rm det}C)^{{-1}}=dq^{{\prime}}dp^{{\prime}}\sqrt{{\rm det}G(q)}$

Ostatnia równość bierze się stąd że $C^{T}GC=I$ , zatem $({\rm det}C)^{2}{\rm det}G=$ . Jest to wiec produkt kanonicznej miary objetości na $M$ ( $dq\sqrt{{\rm det}G(q)}$ ) oraz miary objętości na $T_{q}M$ zadanej przez macierz $G$ (nowa baza $p^{{\prime}}$ jest bazą ortonormalną w przestrzeni $T_{q}M$ .

Na powierzchniach stałej energii $H$ otrzymujemy indukowaną gładką miarę niezmienniczą W szczególnym i najważniejszym dla nas przypadku potoku geodezyjnego powierzchnie stałej energii odpowiadają wiązkom sfer $\sum p_{i}^{{\prime}}^{2}=C$ .