Zagadnienia
12. Potok geodezyjny na rozmaitości o stałej ujemniej krzywiźnie- ważny przykład potoku Anosowa
12.1. Metryka hiperboliczna
Wprowadzimy bardzo ważne wanalizie zespolonej pojęcie płaszczyzny hiperbolicznej
Definicja 12.1
Niech
(czyli - gówna półpłaszczyzna)
W ![]() wprowadzamy metrykę (Riemannowską):
wprowadzamy metrykę (Riemannowską):
Inaczej mówiąc: w nowej metryce, długość ![]() wektora
wektora ![]() należącego do przestrzeni stycznej
należącego do przestrzeni stycznej ![]() jest równa
jest równa
![]() (przez
(przez ![]() oznaczyliśmy normę euklidesową, a przez
oznaczyliśmy normę euklidesową, a przez ![]() - hiperboliczną).
Jeszcze inaczej: w metryce euklidesowej iloczyn skalarny wektorów
- hiperboliczną).
Jeszcze inaczej: w metryce euklidesowej iloczyn skalarny wektorów ![]() stycznych w punkcie
stycznych w punkcie ![]() jest równy
jest równy
![]() . Iloczyn skalarny w nowej metryce jest równy
. Iloczyn skalarny w nowej metryce jest równy
Ćwiczenie 12.1
Sprawdzić że wszystkie homografie (przekształcenia Möbiusa) zachowujące ![]() są postaci:
są postaci:
Stwierdzenie 12.1
Wszystkie homografie zachowujące ![]() są izometriami w metryce hiperbolicznej w
są izometriami w metryce hiperbolicznej w ![]() .
.
Każde takie przekształcenie można zapisać jako złożenie trzech, postaci
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Wystarczy sprawdzić że te trzy przekształcenia są izometriami.
Sprawdzimy trzecie: mamy
. Wystarczy sprawdzić że te trzy przekształcenia są izometriami.
Sprawdzimy trzecie: mamy
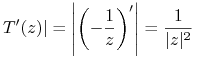 |
Należy sprawdzić że
Równość zachodzi, ponieważ ![]() ,
, ![]()
Ćwiczenie 12.2
Niech ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Wówczas istnieje izometria
. Wówczas istnieje izometria ![]() taka że
taka że ![]() ,
, ![]() .
.
Stwierdzenie 12.2
Geodezyjne w ![]() są to łuki (pół)okręgów prostopadłych do prostej
są to łuki (pół)okręgów prostopadłych do prostej ![]() . Geodezyjną jest też okrąg przechodzący przez punkt w nieskończoności, czyli - każda (pół)prosta prostopadła do prostej
. Geodezyjną jest też okrąg przechodzący przez punkt w nieskończoności, czyli - każda (pół)prosta prostopadła do prostej ![]() .
.
Definicja 12.2
Wprowadzamy metrykę w ![]() (czyli w wiązce wektorów stycznych o długości hiperbolicznej
(czyli w wiązce wektorów stycznych o długości hiperbolicznej ![]() ).
tu rysunek
).
tu rysunek
Niech ![]() . Jeśli
. Jeśli ![]() to miarą odległości między
to miarą odległości między ![]() ,
,![]() jest
jest ![]() - miara kąta między wektorami
- miara kąta między wektorami ![]() ,
,![]() .
Jeśli
.
Jeśli ![]() to istnieje dokładnie jedna geodezyjna
to istnieje dokładnie jedna geodezyjna ![]() przechodząca przez punkty
przechodząca przez punkty ![]() ,
, ![]() . Niech
. Niech ![]() będzie obrazem
będzie obrazem ![]() przy przesunięciu równoległym wzdłuż tej geodezyjnej.
Inaczej- mozna powiedziec tak:
Rozpatrujemy izometrie (przekształcenia Möbiusa) dla których geodezyjna
przy przesunięciu równoległym wzdłuż tej geodezyjnej.
Inaczej- mozna powiedziec tak:
Rozpatrujemy izometrie (przekształcenia Möbiusa) dla których geodezyjna ![]() jest niezmiennicza (jak je znaleźć?) i wybieramy przekształcenie
jest niezmiennicza (jak je znaleźć?) i wybieramy przekształcenie ![]() - taką spośród tych izometrii, która punkt
- taką spośród tych izometrii, która punkt ![]() przekształca na
przekształca na ![]() . Wektor
. Wektor ![]() jest równy
jest równy ![]() .
.
Odległość między ![]() ,
, ![]() definiujemy:
definiujemy:
12.2. Potok geodezyjny w 
Niech ![]() Potok geodezyjny
Potok geodezyjny ![]() można, jak wiemy opisac następujaco: znajdujemy jedyną geodezyjną
można, jak wiemy opisac następujaco: znajdujemy jedyną geodezyjną ![]() taką że
taką że ![]() ,
, ![]() . Po czasie
. Po czasie ![]() mamy
mamy ![]() gdzie
gdzie ![]() ,
, ![]() .
tu rysunek
.
tu rysunek
Rozpatrzmy zatem ![]() . Geodezyjna zawierająca punkt
. Geodezyjna zawierająca punkt ![]() , wypuszczona w kierunku
, wypuszczona w kierunku ![]() to oczywiście półprosta pionowa
to oczywiście półprosta pionowa ![]() . Użyliśmy parametryzacji
. Użyliśmy parametryzacji ![]() ponieważ ma to być parametryzacja odpowiadająca ruchowi ze stała prędkościa:
ponieważ ma to być parametryzacja odpowiadająca ruchowi ze stała prędkościa: ![]() . Mamy:
. Mamy:
Zatem: ![]() , gdzie wektor
, gdzie wektor ![]() jest to wektor
jest to wektor ![]() zaczepiony w punkcie
zaczepiony w punkcie ![]()
NIech teraz ![]() ,
, ![]() . Oczywiście mamy
. Oczywiście mamy
![]() gdzie wektor
gdzie wektor ![]() jest to wektor
jest to wektor ![]() zaczepiony w punkcie
zaczepiony w punkcie ![]()
Zobaczmy jak zmienia się z czasem odległość:
. Mamy:
(dlaczego?)
Podobnie
Ta obserwacja prowadzi do definicji:
Definicja 12.3
Horocykl to każda linia pozioma ![]() i każdy obraz tej linii przy przekształceniu Möbiusa zachowującym
i każdy obraz tej linii przy przekształceniu Möbiusa zachowującym ![]() .
.
tu rysunek
Widzimy że dla każdego ![]() istnieje dokładnie jedna geodezyjna wyznaczona przez ten punkt i wektor i dokładnie dwa horocykle takie że punkt
istnieje dokładnie jedna geodezyjna wyznaczona przez ten punkt i wektor i dokładnie dwa horocykle takie że punkt ![]() należy do horocyklu, zaś wektor
należy do horocyklu, zaś wektor ![]() jest normalny do horocyklu.
Nazwijmy je odpowiednio horocyklem wchodzącym i horocyklem wychodzącym wyznaczonymi przez
jest normalny do horocyklu.
Nazwijmy je odpowiednio horocyklem wchodzącym i horocyklem wychodzącym wyznaczonymi przez ![]()
tu dwa rysunki: geodezyjna, horocykl wchodzący i wychodzący- dla geodezyjnej pionowej i dla geodezyjnej ”typowej”
Niech ![]() . Rozpatrzmy horocykl wchodzący wyznaczony przez
. Rozpatrzmy horocykl wchodzący wyznaczony przez ![]() , W każdym punkcie horocyklu wybieramy wektor normalny do horocyklu , w ten sposób aby wybór był ciągły i aby wektor
, W każdym punkcie horocyklu wybieramy wektor normalny do horocyklu , w ten sposób aby wybór był ciągły i aby wektor ![]() był wybrany. Otrzymujemy jednowymiarową podrozmaitość
był wybrany. Otrzymujemy jednowymiarową podrozmaitość ![]() . Oznaczmy ją przez
. Oznaczmy ją przez ![]() . Podobnie, rozważmy horocykl wychodzący wyznaczony przez
. Podobnie, rozważmy horocykl wychodzący wyznaczony przez ![]() i wybierzmy ciągłą rodzine wektorów normalnych do niego, tak aby wektor
i wybierzmy ciągłą rodzine wektorów normalnych do niego, tak aby wektor ![]() należał do tej rodziny.
Tę podrozmaitość oznaczamy
należał do tej rodziny.
Tę podrozmaitość oznaczamy ![]() .
.
Wyliczenie(powyżej) zmiany odległości przy ![]() dla punktów (i odpowiednich wektorów) zachowuje się przy zastosowaniu izometrii; powyższy racunek prowadzi do Stwierdzenia (szczegóły pomijamy)
dla punktów (i odpowiednich wektorów) zachowuje się przy zastosowaniu izometrii; powyższy racunek prowadzi do Stwierdzenia (szczegóły pomijamy)
Stwierdzenie 12.3
Zbiór ![]() stanowi silną rozmaitość stabilną punktu
stanowi silną rozmaitość stabilną punktu ![]() ; dla każdego
; dla każdego ![]()
![]() gdy
gdy ![]() .
.
Zbiór ![]() jest silną rozmaitością niestabilną punktu
jest silną rozmaitością niestabilną punktu ![]() ; dla każdego
; dla każdego ![]()
![]() gdy
gdy ![]() .
.
Ćwiczenie 12.3
Uzupełnić brakujące szczególy; w szczególności wykazać że wskazany zbiór wyczerpuje cała rozmaitość stabilną (niestabilną); tzn jeżeli ![]() , to
, to ![]()
Oprócz silnej rozmaitości (nie)stabilnej mamy jeszcze słabą rozmaitość (nie)stabilną. Zauważmy że
jeśli ![]() jest punktem (w
jest punktem (w ![]() należącym do geodezyjnej wyznaczonej przez
należącym do geodezyjnej wyznaczonej przez ![]() , to
, to ![]() dla pewnego
dla pewnego ![]() , zatem
, zatem ![]() dla wszystkich
dla wszystkich ![]() .
Mamy więc
.
Mamy więc
Stwierdzenie 12.4
Słaba rozmaitość stabilna ![]() punktu
punktu ![]() jest sumą wszystkich silnych rozmaitości stabilnych punktów
jest sumą wszystkich silnych rozmaitości stabilnych punktów ![]() należących do geodezyjnej wyznaczonej przez
należących do geodezyjnej wyznaczonej przez ![]() .
.
Oczywiscie- symetryczne stwierdzenie mamy dla rozmaitości niestabilnej. Silne rozmaitości są jednowymiarowe, słabe - są dwuwymiarowe.
Przecięciem słabej rozmaitości stabilnej i niestabilnej przechodzącej przez ![]() jest geodezyjna wyznaczona przez
jest geodezyjna wyznaczona przez ![]() , a precyzyjniej- jej podniesienie do
, a precyzyjniej- jej podniesienie do ![]() .
.
Wniosek 12.1
Otrzymalismy w ten sposób globalną foliację stabilna i niestabilną dla potoku geodezyjnego na ![]() .
.
Każdą zwartą orientowalną powierzchnię ![]() można (topologicznie) utożsamiać z przestrzenią ilorazową
można (topologicznie) utożsamiać z przestrzenią ilorazową ![]() dla pewnej dyskretnej podgrupy grupy zachowujących orientację izometrii
dla pewnej dyskretnej podgrupy grupy zachowujących orientację izometrii ![]() (
(![]() jest wówczas grupą podstawową tej powierzchni).
Na rysunku (rysunek: osmiokąt hiperboliczny i dwuprecel i utożsamienia) przedstawiona jest realizacja ”dwuprecla” (czyli sfery z dwiema rączkami) jako hiperbolicznego ośmiokąta
jest wówczas grupą podstawową tej powierzchni).
Na rysunku (rysunek: osmiokąt hiperboliczny i dwuprecel i utożsamienia) przedstawiona jest realizacja ”dwuprecla” (czyli sfery z dwiema rączkami) jako hiperbolicznego ośmiokąta ![]() z odpowiednimi sklejeniami. Po dokonaniu wskazanych utożsamień boków ośmiokąta otrzymujemy (topologicznie) dwuprecel. W szczególności wszystkie wierzchołki ośmiokąta sklejają się w jeden punkt. wszystkie kąty tego ośmiokąta są równe
z odpowiednimi sklejeniami. Po dokonaniu wskazanych utożsamień boków ośmiokąta otrzymujemy (topologicznie) dwuprecel. W szczególności wszystkie wierzchołki ośmiokąta sklejają się w jeden punkt. wszystkie kąty tego ośmiokąta są równe ![]() . (zatem suma jest równa
. (zatem suma jest równa ![]() .
.
Rozpatrzmy izometrie odpowiadające tym utożsamieniom: bok ![]() jest utożsamiany z
jest utożsamiany z ![]() (i odpowiednio pozostałe kroki) przy pomocy hiperbolicznej homografii (przesunięcia wzdłuz geodezyjnej). Grupa
(i odpowiednio pozostałe kroki) przy pomocy hiperbolicznej homografii (przesunięcia wzdłuz geodezyjnej). Grupa ![]() generowana przez te homografie jest dyskretną podgrupą pełnej grupy izometrii. Działając elementami tej grupy na ośmiokąt
generowana przez te homografie jest dyskretną podgrupą pełnej grupy izometrii. Działając elementami tej grupy na ośmiokąt ![]() otrzymujemy ”parkietaż” dysku Poincare'go
otrzymujemy ”parkietaż” dysku Poincare'go ![]() . Ośmiokąt
. Ośmiokąt ![]() (i każda z jego kopii jest dziedziną fundamentalną dla działania grupy
(i każda z jego kopii jest dziedziną fundamentalną dla działania grupy ![]() .
.
Ćwiczenie 12.4
Jakie znaczenie mają w tej konstrukcji miary kątów ośmiokąta ![]() ?
?
Zatem powierzchnia ![]() jest homeomorficzna z przestrzenią ilorazową
jest homeomorficzna z przestrzenią ilorazową ![]() .
Ponieważ grupa
.
Ponieważ grupa ![]() działa przez izometrie, metryka hiperboliczna rzutuje się na metrykę riemannowską na
działa przez izometrie, metryka hiperboliczna rzutuje się na metrykę riemannowską na ![]() ; mazywamy ją też metryką hiperboliczną.
; mazywamy ją też metryką hiperboliczną.
Uwaga 12.1
Na jednej powierzchni istnieje wiele, nieizometrycznych metryk hiperbolicznych.
Ponieważ rzutowanie jest lokalną izometrią, obrazami ( przeciwobrazami) geodezyjnych przy rzutowaniu są geodezyjne.
Potok geodezyjny na rozmaitości ![]() jest więc obrazem potoku na
jest więc obrazem potoku na ![]() , czyli (izometrzycznie) na
, czyli (izometrzycznie) na ![]() .
.
Wykorzystując wykazane wcześniej istnienie globalnej foliacji stabilnej i niestabilnej dla potoku geodezyjnego i powyższą uwagę otrzymujemy
Twierdzenie 12.1
Niech ![]() bedzie zwartą rozmaitością otrzymaną jako przestrzeń ilorazowa
bedzie zwartą rozmaitością otrzymaną jako przestrzeń ilorazowa ![]() (gdzie
(gdzie ![]() jest dyskretną podgrupą grupy zachowujących orientację izometrii
jest dyskretną podgrupą grupy zachowujących orientację izometrii ![]() , z dziedziczoną z
, z dziedziczoną z ![]() metryką hiperboliczną.
Wówczas potok geodezyjny na
metryką hiperboliczną.
Wówczas potok geodezyjny na ![]() jest potokiem Anosowa.
jest potokiem Anosowa.
Wykażemy jeszcze
Twierdzenie 12.2
Jeśli ![]() jest dyskretną podgrupą izometrii
jest dyskretną podgrupą izometrii ![]() zachowujących orientację, taką że
zachowujących orientację, taką że ![]() jest zwarta, to orbity okresowe (czyli podniesienia zamkniętych geodezyjnych) są gęste w
jest zwarta, to orbity okresowe (czyli podniesienia zamkniętych geodezyjnych) są gęste w ![]() .
.
Wybierzmy punkt ![]() i wyznaczoną przez
i wyznaczoną przez ![]() geodezyjną
geodezyjną ![]() . Zatem
. Zatem ![]() . Wówczas krzywa
. Wówczas krzywa ![]() - przeciwobraz
- przeciwobraz ![]() przy rzutowaniu
przy rzutowaniu ![]() jest geodezyjną w
jest geodezyjną w ![]() ; niech
; niech ![]() . Niech
. Niech ![]() będą końcami tej geodezyjnej (rysunek); rozważmy otoczenia
będą końcami tej geodezyjnej (rysunek); rozważmy otoczenia ![]() i
i ![]() tych punktów otrzymane przez łuki geodezyjnych, prostopadłych do
tych punktów otrzymane przez łuki geodezyjnych, prostopadłych do ![]() .
Geodezyjną
.
Geodezyjną ![]() możemy pokryć kopiami dziedziny fundamentalnej
możemy pokryć kopiami dziedziny fundamentalnej ![]() (czyli obrazami
(czyli obrazami ![]() przy działąniu elementami grupy
przy działąniu elementami grupy ![]() ). Ponieważ wszystkie takie kopie
). Ponieważ wszystkie takie kopie ![]() mają tę samą średnicę hiperboliczną; te kopie które są blisko brzegu
mają tę samą średnicę hiperboliczną; te kopie które są blisko brzegu ![]() , mają małą średnicę euklidesową. Można więc znaleźć jakies
, mają małą średnicę euklidesową. Można więc znaleźć jakies ![]() i
i ![]() .
Mamy więc wyróżnione trzy obszary z naszego parkietażu, przecinające geodezyjną
.
Mamy więc wyróżnione trzy obszary z naszego parkietażu, przecinające geodezyjną ![]() :
: ![]() ,
,![]() ,
, ![]() , położone w tej kolejności ”wzdłuż” geodezyjnej
, położone w tej kolejności ”wzdłuż” geodezyjnej ![]() . Niech
. Niech ![]() będzie taką izometrią należącą do
będzie taką izometrią należącą do ![]() , że
, że ![]() . Wówczas
. Wówczas ![]() jest izometrią hiperboliczną; jeden jej punkt stały jest w
jest izometrią hiperboliczną; jeden jej punkt stały jest w ![]() , drugi w
, drugi w ![]() . Niech
. Niech ![]() będzie ”osią” tej izometrii. Wówczas
będzie ”osią” tej izometrii. Wówczas ![]() rzutuje się na zamkniętą geodezyjną na
rzutuje się na zamkniętą geodezyjną na ![]() . Ponieważ otoczenia
. Ponieważ otoczenia ![]() mogą być dowolnie małe, można w ten sposób znaleźć punkt
mogą być dowolnie małe, można w ten sposób znaleźć punkt ![]() blisko
blisko ![]() . Punkt
. Punkt ![]() pod działaniem potoku geodezyjnego ma okresową trajektorię.
pod działaniem potoku geodezyjnego ma okresową trajektorię.




