Zagadnienia

15.1 Definicja entropii
15.2 Związki z entropią metryczną
15.3 Związki ze stopniem przekształcenia

15. O entropii topologicznej

15.1. Definicja entropii

Ograniczymy się do zdefiniowania entropii topologicznej dla ciągłego przekształcenia zwartej przestrzeni metrycznej. Zatem- $X$ jest przestrzenią zwartą metryczną z metryką $d$ , $T:X\to X$ - ciągłym przekształceniem.

Definicja 15.1

Odległość $d_{n}$ między punktami $x,y\in X$ to

$d_{n}(x,y)={\rm max}_{{0\le i<n}}(d(T^{i}x,T^{i}y))$

Definicja 15.2

Mówimy że punkty $x,y,$ są $(n,\varepsilon)$ - rozdzielone, jeśli $d_{n}(x,y)>\varepsilon$ . Zbiór punktów $(n,\varepsilon)$ - rozdzielonych to zbiór w którym każde dwa różne elementy są $(n,\varepsilon)$ - rozdzielone.

Definicja 15.3

Mówimy że punkty $x_{1},\dots x_{k}$ stanowią $(n,\varepsilon)$ -sieć jeśli dla każdego $y\in X$ istnieje $x_{i}$ takie że $D_{n}(y,x_{i})<\varepsilon$ .

Oznaczmy przez $s(n,\varepsilon)$ maksymalną liczebność zbioru $(n,\varepsilon)$ - rozdzielonego, a przez $r(n,\varepsilon)$ - minimalną liczebność $(n\varepsilon)$ -sieci.

Definicja 15.4 (Definicja entropii topologicznej)

Entropia topologiczna $h(T)$ jest to

$\lim _{{\varepsilon\to 0}}\limsup _{{n\to\infty}}\frac{1}{n}\log r(n,\varepsilon)=\lim _{{\varepsilon\to 0}}\limsup _{{n\to\infty}}\frac{1}{n}\log s(n,\varepsilon)$

Ta definicja wymaga uzasadnienia: po pierwsze- w każdej z tych dwóch formuł trzeba sprawdzić czy istnieje granica $\lim _{{\varepsilon\to 0}}$ , po drugie- że obie formuły prowadzą do tego samego wyniku. Sprawdzenie jest zawarte w Stwierdzeniu - poniżej. Dowód pozostawiamy jako ćwiczenie.

Stwierdzenie 15.1

Mamy:

$r(n,\varepsilon)\le s(n,\varepsilon)$

$s(n,2\varepsilon)\le r(n,\varepsilon)$

Ponadto, dla $\varepsilon>\varepsilon^{{\prime}}$ mamy $s(n,\varepsilon^{{\prime}})>s(n,\varepsilon)$ , $r(n,\varepsilon^{{\prime}})>r(n,\varepsilon)$

Przykład 15.1 (Izometria)

Niech $T:X\to X$ będzie izometrią, na przykład- obrotem na okręgu. Wówczas $h(T)=0$ . Istotnie, ustalmy $\varepsilon$ i jakąś $\varepsilon$ sieć (w naszej notacji jest to $(1,\varepsilon)$ - sieć $S$ o liczebości $N=N(\varepsilon)$ . Ponieważ $T$ jest izometrią, ten sam zbiór $S$ jest też $(n\varepsilon)$ - siecią. Zatem liczebność minimalnej $(n,\varepsilon)$ sieci nie rośnie z $n$ . Stąd $h(T)=0$ .

Ćwiczenie 15.1 (Przekształcenie 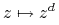$z\mapsto z^{d}$ )

Sprawdzić że entropia tego przekształcenie jest równa $\log d$ . Wskazówka: dla ustalonego $n$ możemy podzielić okrąg na $d^{n}$ łuków, z których każdy jest przekształcany (rozciągany) przez $T^{n}$ na cały okrąg. W każdym takim łuku wybieramy $\frac{1}{\varepsilon}$ równo odległych punktów. Te wszystkie punkty (jest ich razem $\frac{1}{\varepsilon}2^{n}$ ) stanowią zbiór $(n,\varepsilon)$ -rozdzielony.

Ćwiczenie 15.2 (Trudniejsza wersja)

Niech $M$ będzie Riemannowską zwartą rozmaitościa, a $T:M\to M$ - rozszerzającym przekształceniem, tzn istnieje $\lambda>1$ takie że $||DT_{x}(v)||\ge\lambda||v||$ . Uzasadnić że wówczas $T$ jest nakryciem; niech $d$ będzie stopniem tego nakrycia. Wykazać że $h(T)=\log d$ .

Ćwiczenie 15.3

Niech $T$ będzie hiperbolicznym automorfizmem torusa $\mathbb{T}^{2}$ . Wówczas macierz $A$ reprezentująca $T$ ma dwie rzeczywiste wartości własne $\lambda _{1}>1>\lambda _{2}$ . Wykazać że $h(T)=\log\lambda _{1}$ .

Stwierdzenie 15.2

Jeśli $(X,d_{1}),(Y,d_{2})$ są przestrzeniami metrycznymi zwartymi, $T:X\to X$ , $S:Y\to Y$ są sprzężone topologicznie, to $h(T)=h(S)$ .

Ustalmy $\varepsilon>0$ . Istnieje $\delta>0$ takie że $d_{1}(x,y)<\delta\Rightarrow d_{2}(h(x),h(y))<\varepsilon$ . Wynika stąd że jeśli $G$ jest zbiorem $(n,\varepsilon)$ rozdzielonym dla $S$ , to $h^{{-1}}(G)$ jest zbiorem $(n,\delta)$ - rozdzielonym dla $T$ . Zatem

$s_{T}(n,\delta)\ge s_{S}(n,\varepsilon)$

Stąd już łatwo wynika że $h(T)\ge h(S)$ .

∎

15.2. Związki z entropią metryczną

Następujące dwa twierdzenia podajemy bez dowodu:

Twierdzenie 15.1 (Twierdzenie Goodwyna)

Niech $X$ będzie zwartą przestrzenią metryczną, $T:X\to X$ - ciągłym przekształceniem, $\mu$ - miarą borelowską probabilistyczną na $X$ , niezmienniczą dla $T$ . Wówczas:

$h_{\mu}(T)\le h(T)$

Wzmocnieniem jest silniejsze twierdzenie

Twierdzenie 15.2 (Twierdzenie Goodmana)

Przy poprzednich założeniach, mamy

$h(T)=\sum _{\mu}h_{\mu}(T)$

gdzie supremum jest wzięte po wszystkich niezmienniczych borelowskich miarach probabilistycznych.

15.3. Związki ze stopniem przekształcenia

Definicja 15.5

Niech $M$ będzie zwartą, zorientowaną rozmaitością gładką, $T:M\to M$ - gładkim przekształceniem. Na $M$ mamy więc naturalną miarę Lebesge'a. Niech $x$ będzie wartością regularną (tw Sarda gwarantuje że jest to zbiór pełnej miary). Stopniem przekształcenia $t$ w $x$ nazywamy

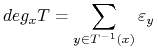$deg_{x}T=\sum _{{y\in T^{{-1}}(x)}}\varepsilon _{y}$

gdzie $\varepsilon _{y}$ jest równe $1$ lub $-1$ w zależności od tego czy $DT(y)$ zmienia czy zachowuje orientację.

Uwaga 15.1

Można sprawdzić że w istocie, stopień $deg_{x}T$ nie zależy od wyboru punktu $x$ - wartości regularnej. Zatem- możemy zdefiniowac $degT$ - jako wspólną wartość $deg_{x}T$ dla wszystkich wartości regularnych $x$ .

Twierdzenie 15.3 (Misiurewicz, Przytycki)

Jeśli $M$ jest gładką orientowalną rozmaitością, a $T:M\to M$ - przekzstałceniem klasy $C^{1}$ to $h(T)\ge\log|degT|$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do teorii Układów Dynamicznych