Zagadnienia
3. Strukturalna stabilność. Układy Morse'a-Smale'a na okręgu
3.1. Pojęcie strukturalnej stabilności dla przekształceń i dla pól wektorowych
Mówiąc nieformalnie, przekształcenie (lub pole wektorowe) chcemy nazwać strukturalnie stabilnym- w jakiejś klasie, jeśli po małym zaburzeniu - w obrębie tej klasy- przekształcenie (pole wektorowe) zachowa swoje własności, czyli dynamika nie zmieni się.
Poniżej formalizujemy tę definicję. Najpierw musimy wprowadzić jakieś formalne pojęcie odległości w przestrzeni przekształceń, dyfeomorfizmów i pól wektorowych.
3.1.1. Metryki i topologie w przestrzeniach przekształceń i w przestrzeniach pól wektorowych
O wszystkich rozmaitościach które tu rozpatrujemy, będziemy zakładali że są klasy ![]() i że są zanurzone w
i że są zanurzone w ![]() (dla pewnego
(dla pewnego ![]() ).
Niech
).
Niech ![]() będzie taką rozmaitościa,
będzie taką rozmaitościa, ![]() , załóżmy dodatkowo że
, załóżmy dodatkowo że ![]() jest zwarta.
Istnieje skończony atlas- rodzina map
jest zwarta.
Istnieje skończony atlas- rodzina map ![]() (można oczywiście założyć że
(można oczywiście założyć że ![]() jest wspólną dziedziną dla wszystkich map z atlasu. Wówczas, dla pewnego
jest wspólną dziedziną dla wszystkich map z atlasu. Wówczas, dla pewnego ![]() obrazy mniejszej kuli
obrazy mniejszej kuli ![]() przy
przy ![]() też pokrywają
też pokrywają ![]() .
Jesli
.
Jesli ![]() to możemy określić odległość
to możemy określić odległość ![]() i
i ![]() :
:
Sprawdzenie następującego faktu pozostawiamy jako zadanie:
Stwierdzenie 3.1
Tak zdefiniowana metryka zależy oczywiście od wyboru atlasu, ale topologia wyznaczona przez te metrykę nie zależy od atlasu, ani od wyboru ![]() .
.
Ponieważ każde pole wektorowe na rozmaitości ![]() zanurzonej w
zanurzonej w ![]() można traktować jak funkcję określoną na rozmaitości, o wartościach w
można traktować jak funkcję określoną na rozmaitości, o wartościach w ![]() , w ten sposób mamy zdefiniowaną topologię
, w ten sposób mamy zdefiniowaną topologię ![]() w przestrzeni pól wektorowych klasy
w przestrzeni pól wektorowych klasy ![]() na
na ![]() .
.
Podobnie, jeśli ![]() jest rozmaitością gładką zanurzoną w
jest rozmaitością gładką zanurzoną w ![]() , to mamy w ten sposób określoną topologię
, to mamy w ten sposób określoną topologię ![]() w przestrzeni przekształceń
w przestrzeni przekształceń ![]() .
.
Będziemy dalej rozpatrywali dyfeomorfizmy klasy ![]() ,
, ![]() .
.
Stwierdzenie 3.2
W przestrzeni wszystkich przekształceń ![]() klasy
klasy ![]() dyfeomorfizmy stanowią otwarty podzbiór.
dyfeomorfizmy stanowią otwarty podzbiór.
3.1.2. Równoważność i sprzężenie między polami wektorowymi i dyfeomorfizmami
Definicja 3.1
Niech ![]() będzie gładką zwartą rozmaitością.
Mówimy że dwa pola wektorowe
będzie gładką zwartą rozmaitością.
Mówimy że dwa pola wektorowe ![]() ,
, ![]() na rozmaitości
na rozmaitości ![]() są topologicznie równoważne jeśli istnieje homeomorfizm
są topologicznie równoważne jeśli istnieje homeomorfizm ![]() przekształcający trajektorie (krzywe całkowe) pola
przekształcający trajektorie (krzywe całkowe) pola ![]() na trajektorie pola
na trajektorie pola ![]() , z zachowaniem orientacji (ale niekoniecznie czasu!)
, z zachowaniem orientacji (ale niekoniecznie czasu!)
Definicja 3.2
Pola ![]() ,
, ![]() na
na ![]() są topologicznie sprzężone jeśli istnieje homeomorfizm
są topologicznie sprzężone jeśli istnieje homeomorfizm ![]() sprzęgający potoki tych pól. Dokładniej- niech
sprzęgający potoki tych pól. Dokładniej- niech ![]() będzie potokiem pola
będzie potokiem pola ![]() ,
, ![]() -potokiem pola
-potokiem pola ![]() . Sprzężenie oznacza że
. Sprzężenie oznacza że
Stwierdzenie 3.3
Jeśli ![]() jest topologiczną równoważnością między polami
jest topologiczną równoważnością między polami ![]() i
i ![]() to
to
-
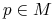 jest punktem stacjonarnym pola
jest punktem stacjonarnym pola 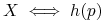 jest punktem stacjonarnym pola
jest punktem stacjonarnym pola 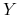 .
. -
trajektoria pola
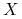 przechodząca przez punkt
przechodząca przez punkt 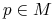 jest zamknięta wtedy i tylko wtedy gdy trajektoria pola
jest zamknięta wtedy i tylko wtedy gdy trajektoria pola 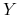 przechodząca przez punkt
przechodząca przez punkt 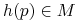 jest zamknięta.
jest zamknięta. -
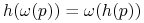
Ćwiczenie 3.1
Zbudować sprzężenie topologiczne między polami na płaszczyźnie:
Ćwiczenie 3.2
Pole wektorowe na płaszczyźnie
nie jest sprzężone i nie jest równowazne żadnemu z pól ![]() .
.
Definicja 3.3
Niech ![]() będzie gładką rozmaitością,
będzie gładką rozmaitością, ![]() - dyfeomorfizmy. Mówimy że
- dyfeomorfizmy. Mówimy że ![]() i
i ![]() są topologicznie sprzężone jeśli istnieje homeomorfizm
są topologicznie sprzężone jeśli istnieje homeomorfizm ![]() taki że
taki że ![]() .
.
3.1.3. Strukturalna stabilność
Definicja 3.4
Niech ![]() będzie zwartą rozmaitością;
będzie zwartą rozmaitością; ![]() - polem wektorowym klasy
- polem wektorowym klasy ![]() na
na ![]() . Mówimy że
. Mówimy że ![]() jest
jest ![]() - strukturalnie stabilne jeśli istnienie otoczenie
- strukturalnie stabilne jeśli istnienie otoczenie ![]() pola
pola ![]() w
w ![]() topologii w przestrzeni pól wektorowych na
topologii w przestrzeni pól wektorowych na ![]() takie że każde pole wektorowe
takie że każde pole wektorowe ![]() jest topologicznie równoważne polu
jest topologicznie równoważne polu ![]() .
.
Definicja 3.5
Niech ![]() będzie zwartą rozmaitością,
będzie zwartą rozmaitością, ![]() dyfeomorfizmem klasy
dyfeomorfizmem klasy ![]() . Mówimy że
. Mówimy że ![]() jest strukturalnie stabilne jeśli istnieje otoczenie
jest strukturalnie stabilne jeśli istnieje otoczenie ![]() w
w ![]() takie że każdy dyfeomorfizm
takie że każdy dyfeomorfizm ![]() jest topologicznie sprzężony z
jest topologicznie sprzężony z ![]() .
.
3.2. Strukturalnie stabilne dyfeomorfizmy okręgu
W tym rozdziale podamy pełną charakteryzację ![]() - strukturalnie stabilnych dyfeomorfizmów okręgu.
- strukturalnie stabilnych dyfeomorfizmów okręgu.
Definicja 3.6
Dyfeomorfizm ![]() klasy
klasy ![]() zachowujacy orientację
nazywamy dyfeomorfizmem Morse'a- Smale'a jeśli
zachowujacy orientację
nazywamy dyfeomorfizmem Morse'a- Smale'a jeśli ![]() oraz dla każdego
punktu okresowego
oraz dla każdego
punktu okresowego ![]() mamy
mamy ![]() (gdzie
(gdzie ![]() jest okresem, wspólnym dla wszystkich punktów okresowych).
(Punkt okresowy o tej własności nazywamy niezdegenerowanym.)
jest okresem, wspólnym dla wszystkich punktów okresowych).
(Punkt okresowy o tej własności nazywamy niezdegenerowanym.)
Twierdzenie 3.1 (O strukturalnie stabilnych dyfeomorfizmach okręgu)
-
Dyfeomorfizm
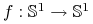 jest strukturalnie stabilny wtedy i tylko wtedy gdy jest dyfeomorfizmem Morse'a-Smale'a.
jest strukturalnie stabilny wtedy i tylko wtedy gdy jest dyfeomorfizmem Morse'a-Smale'a. -
Dyfeomorfizmy Morse'a Smale'a stanowią gęsty podzbiór przestrzeni dyfeomorfizmów
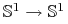 w
w 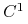 metryce.
metryce.
Najpierw wykażemy że dyfeomorfizm Morse'a-Smale'a jest strukturalnie stabilny. Niech ![]() .
Przechodząc do iteracji
.
Przechodząc do iteracji ![]() mamy
mamy ![]() . Ponieważ wszystkie punkty stałę dla
. Ponieważ wszystkie punkty stałę dla ![]() są niezdegenerowane, jest ich skonczenie wiele. Oznaczmy je
są niezdegenerowane, jest ich skonczenie wiele. Oznaczmy je ![]() . Oczywiście istnieje otoczenie punktów
. Oczywiście istnieje otoczenie punktów ![]() ,
, ![]() takie ze dla
takie ze dla ![]()
![]() , zas dla
, zas dla ![]()
![]() . Stąd widac że jeśli zaburzyć
. Stąd widac że jeśli zaburzyć ![]() do
do ![]() na tyle mało w
na tyle mało w ![]() że
że ![]() - odpowiednie podniesienie
- odpowiednie podniesienie ![]() jest
jest ![]() blisko
blisko ![]() ,to
,to ![]() ma tyle samo punktów stałych co
ma tyle samo punktów stałych co ![]() i są one tego samego typu (zródła lub ścieki).
Okrąg jest więc podzielony przez punkty okresowe
i są one tego samego typu (zródła lub ścieki).
Okrąg jest więc podzielony przez punkty okresowe ![]() na łuki miedzy odpowiadajacymi sobie wzajemnie punktami okresowymi (dla
na łuki miedzy odpowiadajacymi sobie wzajemnie punktami okresowymi (dla ![]() i tak samo dla
i tak samo dla ![]() ).
Wybierzmy jeden z tych łuków
).
Wybierzmy jeden z tych łuków ![]() i odpowiadający mu łuk
i odpowiadający mu łuk ![]() Pokażemy jak zbudowac homeomorfizm sprzęgający
Pokażemy jak zbudowac homeomorfizm sprzęgający ![]() i
i ![]() na odcinkach
na odcinkach ![]() i
i ![]() .
.
(tu rysunek)
Wybieramy dowolny punkt ![]() i dowolny punkt
i dowolny punkt ![]() .
Przekształcamy odcinek
.
Przekształcamy odcinek ![]() na
na ![]() jakimkolwiek homeomorfizmem
jakimkolwiek homeomorfizmem ![]() .
Ponieważ
.
Ponieważ ![]() , można przedłużyc
, można przedłużyc ![]() na cały odcinek
na cały odcinek ![]() kładąc
kładąc ![]() . Mamy więc na odcinku
. Mamy więc na odcinku ![]()
| (3.1) |
Przedłużamy teraz sprzężenie ![]() na całą orbitę odcinka
na całą orbitę odcinka ![]()
![]() tak aby otrzymać sprzężenie pomiędzy
tak aby otrzymać sprzężenie pomiędzy ![]() i
i ![]() . Jest tylko jeden sposób na przedłużenie
. Jest tylko jeden sposób na przedłużenie ![]() : trzeba położyć
: trzeba położyć
Ćwiczenie 3.3
Sprawdzić, używając równości (3.1) że tak zdefiniowane rozszerzenie ![]() rzeczywiscie jest sprzężeniem pomiędzy
rzeczywiscie jest sprzężeniem pomiędzy ![]() i
i ![]() .
.
Zatem wykazaliśmy strukturalną stabilność dyfeomorfizmów Morse'a-Smale'a.
Pokażemy teraz że jesli ![]() jest dyfeomorfizmem klasy
jest dyfeomorfizmem klasy ![]() i
i ![]() to można
to można ![]() zaburzyć dowolnie mało w metryce
zaburzyć dowolnie mało w metryce ![]() tak że zmieni się liczba obrotu.
tak że zmieni się liczba obrotu.
Uzyjemy sprzegającego z obrotem o kąt ![]() homeomorfizmu, danego przez twierdzenie Denjoy.
homeomorfizmu, danego przez twierdzenie Denjoy.
![]() . Rozpatrujemy teraz rodzinę dyfeomorfizmów
. Rozpatrujemy teraz rodzinę dyfeomorfizmów
(w poniesieniu odpowiada to wzięciu funkcji ![]() ).
Zauważmy że
).
Zauważmy że ![]() jest przekształceniem okręgu o dodatniej liczbie obrotu ( w podniesieniu mamy
jest przekształceniem okręgu o dodatniej liczbie obrotu ( w podniesieniu mamy
![]() ).
).
Zatem ![]() ma większa liczbę obrotu niż
ma większa liczbę obrotu niż ![]() . Stad i samo
. Stad i samo ![]() ma większą niż
ma większą niż ![]() liczbę obrotu.
liczbę obrotu.
Skorzystamy z następującego faktu:
Stwierdzenie 3.4
Każdy dyfeomorfizm okręgu klasy ![]() można przybliżyć w metryce
można przybliżyć w metryce ![]() dyfeomorfizmami klasy
dyfeomorfizmami klasy ![]() (a nawet
(a nawet ![]() ).
).
Z poprzedniego stwierdzenia wynika od razu ze każdy dyfeomorfizm klasy ![]() ktory jest
ktory jest ![]() strukturalnie stabilny musi mieć wymierną liczbę obrotu.
strukturalnie stabilny musi mieć wymierną liczbę obrotu.
Wykażemy teraz że dyfeomorfizmy Morse'a-Smale'a klasy ![]() stanowią gęsty podzbiór w metryce
stanowią gęsty podzbiór w metryce ![]() w przestrzeni
w przestrzeni ![]() dyfeomorfizmów okręgu.
dyfeomorfizmów okręgu.
Weźmy dowolny dyfeomorfizm ![]() klasy
klasy ![]() . W jego dowolnie małym otoczeniu możemy znaleźć dyfeomorfizm
. W jego dowolnie małym otoczeniu możemy znaleźć dyfeomorfizm ![]() klasy
klasy ![]() . Jeśli ten dyfeomorfizm ma wymierną liczbe obrotu, ustalamy go. Jeśli nie- to zaburzamy
. Jeśli ten dyfeomorfizm ma wymierną liczbe obrotu, ustalamy go. Jeśli nie- to zaburzamy ![]() w taki sam sposób jak powyżej, tworząc rodzinę
w taki sam sposób jak powyżej, tworząc rodzinę ![]() . Ponieważ, jak widzieliśmy, w ten sposób można zwiększyć liczbę obrotu i ponieważ liczba obrotu dla
. Ponieważ, jak widzieliśmy, w ten sposób można zwiększyć liczbę obrotu i ponieważ liczba obrotu dla ![]() jest ciąglą funkcją
jest ciąglą funkcją ![]() , istnieje dowolnie małe
, istnieje dowolnie małe ![]() takie że
takie że ![]() ma wymierną liczbę obrotu. Zatem- w dowolnie małym
ma wymierną liczbę obrotu. Zatem- w dowolnie małym ![]() otoczeniu funkcji
otoczeniu funkcji ![]() możemy wskazać dyfeomorfizm
możemy wskazać dyfeomorfizm ![]() klasy
klasy ![]() z wymierną liczbą obrotu. Ustalmy ten dyfeomorfizm, nazwijmy go
z wymierną liczbą obrotu. Ustalmy ten dyfeomorfizm, nazwijmy go ![]() .
.
Pokażemy że ![]() można zaburzyć dowolnie mało w metryce
można zaburzyć dowolnie mało w metryce ![]() (więc tym bardziej-w
(więc tym bardziej-w ![]() ) tak żeby wszystkie punkty okresowe stały się niezdegenerowane.
) tak żeby wszystkie punkty okresowe stały się niezdegenerowane.
Najpierw załóżmy że istnieje przynajmniej jeden punkt okresowy niezdegenerowany dla ![]() . Ten punkt dzieli
okrąg na
. Ten punkt dzieli
okrąg na ![]() łuków; w podniesieniu mamy odcinek długości
łuków; w podniesieniu mamy odcinek długości ![]() podzielony na
podzielony na ![]() odcinków. Ustalamy jeden z tych odcinków, nazwijmy go
odcinków. Ustalamy jeden z tych odcinków, nazwijmy go ![]() . Weźmy teraz nieco mniejszy odcinek
. Weźmy teraz nieco mniejszy odcinek ![]() taki że w
taki że w ![]() nie ma żadnych punktów okresowych dla
nie ma żadnych punktów okresowych dla ![]() (a dokładniej: podniesień punktów okresowych).
Taki odcinek można wybrać bo trajektoria okresowa do której należa punkty
(a dokładniej: podniesień punktów okresowych).
Taki odcinek można wybrać bo trajektoria okresowa do której należa punkty ![]() jest niezdegenerowana.
Zmniejszając odcinek
jest niezdegenerowana.
Zmniejszając odcinek ![]() możemy też założyć że istnieje
możemy też założyć że istnieje ![]() takie że jeśli
takie że jeśli ![]() jest dyfeomorfizmem
okręgu
jest dyfeomorfizmem
okręgu ![]() - bliskim
- bliskim ![]() w metryce
w metryce ![]() i
i ![]() ,
, ![]() to w odcinku
to w odcinku ![]() nie ma innych punktów stałych dla
nie ma innych punktów stałych dla ![]() .
Niech
.
Niech ![]() będzie gładką funkcją określoną w
będzie gładką funkcją określoną w ![]() taką że
taką że ![]() na odcinku
na odcinku ![]() ,
, ![]() w otoczeniu punktów
w otoczeniu punktów ![]() . Przedłużamy funkcję
. Przedłużamy funkcję ![]() do równej zero poza
do równej zero poza ![]() .
(rysunek
Określamy nową rodzinę funkcji (w podniesieniu )
.
(rysunek
Określamy nową rodzinę funkcji (w podniesieniu ) ![]() .
Dla małych
.
Dla małych ![]() funkcja
funkcja ![]() (odpowiednio
(odpowiednio ![]() ) jest
) jest ![]() - bliska
- bliska ![]() (odpowiednio-
(odpowiednio- ![]() ). Zatem jeśli
). Zatem jeśli ![]() jest punktem stałym dla
jest punktem stałym dla ![]() to albo
to albo ![]() , albo
, albo ![]() , albo
, albo ![]() .
Zauważamy teraz że
.
Zauważamy teraz że ![]() jest punktem okresowym zdegenerowanym dla
jest punktem okresowym zdegenerowanym dla ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy ![]() jest punktem krytycznym i miejscem zerowym dla funkcji
jest punktem krytycznym i miejscem zerowym dla funkcji ![]() .
Ponieważ każda trajektoria długości
.
Ponieważ każda trajektoria długości ![]() zawarta w
zawarta w ![]() (a wlaściwie: jej podniesienie)
przecina dokładnie raz odcinek
(a wlaściwie: jej podniesienie)
przecina dokładnie raz odcinek ![]() , a funkcja
, a funkcja ![]() pozostaje
niezmieniona poza tym odcinkiem, widzimy że na odcinku
pozostaje
niezmieniona poza tym odcinkiem, widzimy że na odcinku ![]() mamy
mamy ![]() . Zatem jeśli istnieją punkty okresowe
zdegenerowane dla
. Zatem jeśli istnieją punkty okresowe
zdegenerowane dla ![]() , to
, to ![]() jest wartością krytyczną
dla funkcji
jest wartością krytyczną
dla funkcji ![]() . Aby pokazać że dla wielu
. Aby pokazać że dla wielu ![]() to jest
niemożliwe, skorzystamy z prostej wersji twierdzenia Sarda:
to jest
niemożliwe, skorzystamy z prostej wersji twierdzenia Sarda:
Lemat 3.1 (Twierdzenie Sarda na prostej)
Niech ![]() będzie funkcją klasy
będzie funkcją klasy ![]() . Wówczas zbiór wartości krytycznych dla
. Wówczas zbiór wartości krytycznych dla ![]() ma miarę Lebesgue'a równą zero.
ma miarę Lebesgue'a równą zero.
Korzystając z tego lematu , możemy więc wybrać dowolnie małe ![]() , dla którego
, dla którego ![]() nie jest wartością krytyczną dla
nie jest wartością krytyczną dla ![]() . Zatem nasze
. Zatem nasze ![]() nie ma nezdegenerowanych punktów okresowych.
nie ma nezdegenerowanych punktów okresowych.
Dla zakończenia dowodu pozostaje upewnić się że zawsze można mało zaburzyć ![]() aby otrzymać przynajmniej jeden punkt okresowy niezdegenerowany.
aby otrzymać przynajmniej jeden punkt okresowy niezdegenerowany.
Przykład 3.1
Rozważmy przekształcenie ![]() dane wzorem
dane wzorem ![]() .
Jesli
.
Jesli ![]() to
to ![]() jest ściśle rosnąca i
jest ściśle rosnąca i ![]() . Zatem
. Zatem ![]() wyznacza dyfeomorfizm okręgu.
wyznacza dyfeomorfizm okręgu.
![]() ma
ma ![]() punktów stałych; są to punkty odpowiadające wartościom na prostej
punktów stałych; są to punkty odpowiadające wartościom na prostej ![]() .
Dla
.
Dla ![]() nieparzystych mamy ścieki, dla
nieparzystych mamy ścieki, dla ![]() parzystych-źródła.
parzystych-źródła.
Przykład 3.2
Teraz niech ![]() .
Tym razem mamy dwie orbity okresowe o okresie
.
Tym razem mamy dwie orbity okresowe o okresie ![]() ; punkty
; punkty ![]() stanowią orbitę odpychającą, zaś punkty
stanowią orbitę odpychającą, zaś punkty
![]() - orbitę przyciągającą.
- orbitę przyciągającą. ![]() .
.
3.3. Strukturalnie stabilne pola wektorowe na okręgu
Poniżej- ważna definicja strukturalniej stabilności
Definicja 3.7
Mówimy że pole wektorowe ![]() na zwartej gładkiej rozmaitości jest strukturalnie stabilne jeśli istnieje otoczenie
na zwartej gładkiej rozmaitości jest strukturalnie stabilne jeśli istnieje otoczenie ![]() pola
pola ![]() w metryce
w metryce ![]() , takie że dla każdego
, takie że dla każdego ![]() istnieje homeomorfizm
istnieje homeomorfizm ![]() przekształcający trajektorie pola
przekształcający trajektorie pola ![]() na trajektorie pola
na trajektorie pola ![]() .
.
Uwaga 3.1
Tu pojawia się konieczność precyzyjnego określenia ![]() topologii w przestrzeni pól wektorowych na zwartej głądkiej rozmaitości.
topologii w przestrzeni pól wektorowych na zwartej głądkiej rozmaitości.
W tym rozdziale ograniczamy się jednak do pól wektorowych na okręgu ![]() . Ustalmy orientację na
. Ustalmy orientację na ![]() ; w każdym punkcie
; w każdym punkcie ![]() mamy więc wyznaczony jednostkowy wektor styczny, dodatnio zorientowany
mamy więc wyznaczony jednostkowy wektor styczny, dodatnio zorientowany ![]() . Pole wektorowe jest więc wyznaczone przez funkcję
. Pole wektorowe jest więc wyznaczone przez funkcję ![]() (
(![]() ), lub- równoważnie - przez okresową funkcję
), lub- równoważnie - przez okresową funkcję ![]() .
Zauważmy że jeśli
.
Zauważmy że jeśli ![]() jest potokiem pola wektorowego na prostej
jest potokiem pola wektorowego na prostej ![]() , to
, to ![]() (gdzie
(gdzie ![]() jest rzutowaniem z prostej na okrąg) jest potokiem pola wektorowego na okręgu
jest rzutowaniem z prostej na okrąg) jest potokiem pola wektorowego na okręgu ![]() .
Następującą charakteryzację
.
Następującą charakteryzację ![]() strukturalnie stabilnych pól wektorowych na
strukturalnie stabilnych pól wektorowych na ![]() można udowodnić modyfikując (a właściwie- upraszczając) odpowiedni dowód dla dyfeomorfizmów.
można udowodnić modyfikując (a właściwie- upraszczając) odpowiedni dowód dla dyfeomorfizmów.
Stwierdzenie 3.5
Pole wektorowe ![]() klasy
klasy ![]() jest
jest ![]() -strukturalnie stabilne wtedy i tylko wtedy gdy wszystkie stacjonarne punkty pola
-strukturalnie stabilne wtedy i tylko wtedy gdy wszystkie stacjonarne punkty pola ![]() są niezdegenerowane (tzn. jeśli
są niezdegenerowane (tzn. jeśli ![]() , to
, to ![]() . Zbiór takich pól wektorowcyh na
. Zbiór takich pól wektorowcyh na ![]() jest otwarty i gęsty w
jest otwarty i gęsty w ![]() topologii.
topologii.





