Zagadnienia
6. Rozmaitości stabilne i niestabilne. Twierdzenia o ich istnieniu i własnościach
6.1. Hiperboliczne punkty stałe i stacjonarne
Definicja 6.1
Niech ![]() będzie przestrzenią liniową skończonego wymiaru nad
będzie przestrzenią liniową skończonego wymiaru nad ![]() (albo nad
(albo nad ![]() ), niech
), niech ![]() będzie odwracalnym przekształceniem liniowym. Mówimy że
będzie odwracalnym przekształceniem liniowym. Mówimy że ![]() jest przekształceniem hiperbolicznym jeśli wszystkie wartości własne
jest przekształceniem hiperbolicznym jeśli wszystkie wartości własne ![]() mają moduł różny od
mają moduł różny od ![]() .
.
Definicja 6.2
Niech ![]() będzie dyfeomorfizmem określonym na otoczeniu
będzie dyfeomorfizmem określonym na otoczeniu ![]() w
w ![]() , takim że
, takim że ![]() i różniczka
i różniczka ![]() jest hiperbolicznym przekształceniem liniowym. Wówczas mówimy że
jest hiperbolicznym przekształceniem liniowym. Wówczas mówimy że ![]() jest hiperbolicznym punktem stałym dla
jest hiperbolicznym punktem stałym dla ![]() .
Jeśli
.
Jeśli ![]() jest okresowy dla
jest okresowy dla ![]() ,
, ![]() i różniczka
i różniczka ![]() jest hiperbolicznym przekształceniem liniowym, to mówimy że
jest hiperbolicznym przekształceniem liniowym, to mówimy że ![]() jest hiperbolicznym punktem okresowym.
jest hiperbolicznym punktem okresowym.
Definicja 6.3
Jeśli ![]() jest dyfeomorfizmem rozmaitości
jest dyfeomorfizmem rozmaitości ![]() ,
, ![]() to mówimy że
to mówimy że ![]() jest punktem stałym hiperbolicznym jeśli dla mapy
jest punktem stałym hiperbolicznym jeśli dla mapy ![]() , określonej na otoczeniu zera, takiej że
, określonej na otoczeniu zera, takiej że ![]() , punkt
, punkt ![]() jest hiperbolicznym punktem stałym przekształcenia
jest hiperbolicznym punktem stałym przekształcenia ![]() (ta definicja nie zależy od wyboru mapy!)
(ta definicja nie zależy od wyboru mapy!)
Definicja 6.4
Niech ![]() będzie polem wektorowym klasy
będzie polem wektorowym klasy ![]() , określonym w pewnym otoczeniu
, określonym w pewnym otoczeniu ![]() w
w
![]() takim że
takim że ![]() i rózniczka
i rózniczka ![]() pola
pola ![]() w punkcie
w punkcie ![]() (rozumianego jako funkcja o wartościach w
(rozumianego jako funkcja o wartościach w
![]() ) nie ma wartości własnych o zerowej części rzeczywistej.
Taki punkt stacjonarny
) nie ma wartości własnych o zerowej części rzeczywistej.
Taki punkt stacjonarny ![]() nazywamy hiperbolicznym.
nazywamy hiperbolicznym.
Definicja 6.5
Niech ![]() będzie polem wektorowym klasy
będzie polem wektorowym klasy ![]() , określonym w pewnym otoczeniu
, określonym w pewnym otoczeniu ![]() (
(![]() - gładka rozmaitość).
- gładka rozmaitość). ![]() . Mówimy że
. Mówimy że ![]() jest punktem stacjonarnym hiperbolicznym dla pola
jest punktem stacjonarnym hiperbolicznym dla pola ![]() jeśli dla mapy
jeśli dla mapy ![]() określonej na otoczeniu zera, takiej że
określonej na otoczeniu zera, takiej że ![]() , punkt
, punkt ![]() jest punktem stacjonarnym hiperbolicznym dla pola
jest punktem stacjonarnym hiperbolicznym dla pola
![]() (ta definicja nie zależy od wyboru mapy).
(ta definicja nie zależy od wyboru mapy).
6.2. Twierdzenia Grobmana- Hartmana
To twierdzenie jest znane z kursu Jakościowej Teorii Równań Różniczkowych; przytaczamy je w wersji potrzebnej do naszych celów i podajemy szkic dowodu.
Twierdzenie 6.1 (Twierdzenie Grobmana-Hartmana o lokalnej stabilności)
-
Wersja dla dyfeomorfizmów: Niech
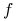 będzie dyfeomorfizmem określonym na otoczeniu
będzie dyfeomorfizmem określonym na otoczeniu 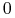 w
w 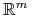 ,takim że
,takim że 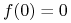 i różniczka
i różniczka 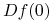 jest hiperbolicznym przekształceniem liniowym. Wówczas istnieje homeomorfizm
jest hiperbolicznym przekształceniem liniowym. Wówczas istnieje homeomorfizm 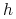 określony w pewnym otoczeniu zera
określony w pewnym otoczeniu zera 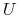 taki że dla
taki że dla 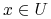 mamy:
mamy: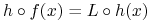
-
Wersja dla potoków: Niech
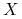 będzie polem wektorowym klasy
będzie polem wektorowym klasy 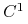 , określonym w pewnym otoczeniu zera w
, określonym w pewnym otoczeniu zera w
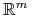 takim że
takim że 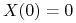 i rózniczka
i rózniczka 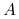 pola
pola 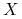 w punkcie
w punkcie 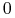 (rozumianego jako funkcja o wartościach w
(rozumianego jako funkcja o wartościach w
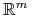 ) nie ma wartości własnych o zerowej części rzeczywistej. Wówczas istnieje homeomorfizm
) nie ma wartości własnych o zerowej części rzeczywistej. Wówczas istnieje homeomorfizm 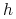 określony w pewnym otoczeniu zera
określony w pewnym otoczeniu zera 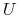 taki że dla
taki że dla 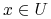 potok
potok 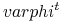 pola wektowego
pola wektowego 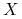 jest
sprzężony przez
jest
sprzężony przez 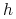 R z potokiem
R z potokiem 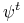 pola liniowego z macierzą
pola liniowego z macierzą 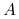 (czyli z potokiem
(czyli z potokiem 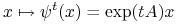 ).
).
Podamy najpierw szkic dowodu dla dyfeomorfizmów.
Lemat 6.1
Niech ![]() będzie przestrzenią Banacha.
Niech
będzie przestrzenią Banacha.
Niech ![]() będzie przekształceniem liniowym ciągłym
będzie przekształceniem liniowym ciągłym ![]() , takim że
, takim że ![]() , niech
, niech ![]() będzie odwracalnym przekształceniem liniowym takim że
będzie odwracalnym przekształceniem liniowym takim że ![]() . Wówczas
. Wówczas
-
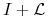 jest odwracalne i
jest odwracalne i 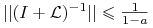
-
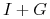 jest odwracalne i
jest odwracalne i 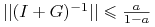
Lemat 6.2
Dla hiperbolicznego przekształcenia liniowego ![]() istnieje norma w
istnieje norma w ![]() taka że jeśli
taka że jeśli ![]() jest rozkładem na (niezmiennicze) podprzestrzenie odpowiadające wartosciom własnym mniejszym (większym) co do modułu od
jest rozkładem na (niezmiennicze) podprzestrzenie odpowiadające wartosciom własnym mniejszym (większym) co do modułu od ![]() , to
, to ![]() ,
, ![]()
Następujące Stwierdzenie jest kluczowym krokiem dowodu:
Stwierdzenie 6.1
Niech ![]() będzie hiperbolicznyn przekształceniem liniowym
Istnieje
będzie hiperbolicznyn przekształceniem liniowym
Istnieje ![]() takie że jeśli
takie że jeśli ![]() spełnia warunek Lipschitza ze stałą mniejszą niż
spełnia warunek Lipschitza ze stałą mniejszą niż ![]() , to
, to
![]() i
i ![]() są topologicznie sprzężone w
są topologicznie sprzężone w ![]() czyli istnieje homeomorfizm
czyli istnieje homeomorfizm ![]() taki że
taki że
Szukamy homeomorfizmu ![]() w postaci
w postaci ![]() , gdzie
, gdzie ![]() .
Żądamy więc aby
.
Żądamy więc aby
| (6.1) |
czyli
| (6.2) |
Sprawdzimy że równanie (6.2) ma dokładnie jedno rozwiązanie w ![]() .
Rozpatrzmy przekształcenie liniowe
.
Rozpatrzmy przekształcenie liniowe
![]() określone
określone ![]() .
.
Lemat 6.3
Przekształcenie ![]() jest odwracalne. Ponadto
jest odwracalne. Ponadto
Możemy zapisać
czyli jako złożenie dwóch operacji: najpierw ![]() , potem
, potem ![]() .
Wystarczy ozywiście sprawdzić że ta pierwsza operacja jest odwracalna, a w tym celu wystarczy sprawdzić że przekształcenie liniowe
.
Wystarczy ozywiście sprawdzić że ta pierwsza operacja jest odwracalna, a w tym celu wystarczy sprawdzić że przekształcenie liniowe ![]() ma normę mniejszą niż
ma normę mniejszą niż ![]() . Możemy zapisać
. Możemy zapisać ![]() (korzystając z rozkładu
(korzystając z rozkładu ![]() ), i rozłożyć w ten sposób przestrzeń
), i rozłożyć w ten sposób przestrzeń ![]() na sumę prostą
na sumę prostą ![]() . Nasze przekształcenie zachowuje ten rozkład. Funkcja
. Nasze przekształcenie zachowuje ten rozkład. Funkcja ![]() jest przekształcana na
jest przekształcana na ![]() To ostatnie przekształcenie jest odwracalne (odwrotne to oczywiście
To ostatnie przekształcenie jest odwracalne (odwrotne to oczywiście ![]() ) i ma normę mniejszą niż
) i ma normę mniejszą niż ![]() . Z lematu 6.1 wynika że
. Z lematu 6.1 wynika że ![]() jest odwracalne. Podobnie sprawdzamy że
jest odwracalne. Podobnie sprawdzamy że ![]() jest odwracalne.
jest odwracalne.
Szukane ![]() jest postaci
jest postaci
Zauważmy że, przy małym ![]() , przekształcenie
, przekształcenie ![]() jest kontrakcją.
Tak jest bo
jest kontrakcją.
Tak jest bo
Stąd wynika że istnieje dokładnie jeden punkt stały tego przekształcenia w ![]() .
Otrzymujemy zatem
.
Otrzymujemy zatem ![]() spełniające (6.1). Do końca dowodu potrzeba wykazać że
spełniające (6.1). Do końca dowodu potrzeba wykazać że ![]() jest homeomorfizmem.
Możemy w tym celu skorzystać z jedyności rozwiązania.
Zauważamy (należy to sprawdzić) że w ten sam sposób jak powyżej można uzyskać również jedyne rozwiązanie nieco ogólniejszego zagadnienia:
jest homeomorfizmem.
Możemy w tym celu skorzystać z jedyności rozwiązania.
Zauważamy (należy to sprawdzić) że w ten sam sposób jak powyżej można uzyskać również jedyne rozwiązanie nieco ogólniejszego zagadnienia:
(o ile ![]() ,
, ![]() spełniają warunek Lipschitza z odpowiednio małą stałą).
Zatem, jeśli
spełniają warunek Lipschitza z odpowiednio małą stałą).
Zatem, jeśli ![]() spełnia
spełnia
to
To złożenie ![]() jest oczywiście postaci
jest oczywiście postaci ![]() plus jakaś funkcja z
plus jakaś funkcja z ![]() , i - sprzęga
, i - sprzęga ![]() z samym sobą. Z jedyności rozwiązania wynika że
z samym sobą. Z jedyności rozwiązania wynika że
Tak samo sprawdzamy że ![]() . W takim razie
. W takim razie ![]() jest homeomorfizmem.
jest homeomorfizmem.
Dla zakończenia dowodu twierdzenia należy jeszcze wykazać
Lemat 6.4
Jeśli ![]() spełnia założenia twierdzenia to dla dowolnego
spełnia założenia twierdzenia to dla dowolnego ![]() istnieje przedłużenie
istnieje przedłużenie ![]() z pewnego otoczenia zera
z pewnego otoczenia zera ![]() na całe
na całe ![]() , postaci
, postaci ![]() , gdzie
, gdzie ![]() i stała Lipschitza
i stała Lipschitza ![]() nie przekracza
nie przekracza ![]() .
.
Dowód polega na zastosowaniu standardowej procedury: Weźmy funkcję ![]() klasy
klasy ![]() określoną w
określoną w ![]() taką że
taką że ![]() dla
dla ![]() ,
, ![]() dla
dla ![]() . Oczywiście
. Oczywiście ![]() spełna warunek Lipschitza z pewną stała
spełna warunek Lipschitza z pewną stała ![]() . Ponieważ
. Ponieważ ![]() to funkcja
to funkcja ![]() spełnia
spełnia ![]() ,
, ![]() ;
; ![]() jeśli
jeśli ![]() i
i ![]() jest odpowiednio bliskie zera.
jest odpowiednio bliskie zera.
Wówczas funkcja
jest szukanym rozszerzeniem.
∎Pozostaje udowodnić twierdzenie dla potoku pola wektorowego.
Wystarczy udowodnić twierdzenie dla pola wektorowego określonego w otoczeniu zera w ![]() .
Rozważmy więc równanie różniczkowe zadane przez
.
Rozważmy więc równanie różniczkowe zadane przez
gdzie ![]() i macierz
i macierz ![]() nie ma wartości własnych o zerowej części rzeczywistej.
nie ma wartości własnych o zerowej części rzeczywistej.
Podobnie jak poprzednio, modyfikujemy funkcje ![]() do
do ![]() . Funkcja
. Funkcja ![]() jest równa
jest równa ![]() na pewnym otoczeniu zera i równa
na pewnym otoczeniu zera i równa ![]() poza pewnym (większym) otoczeniem zera.
poza pewnym (większym) otoczeniem zera.
Niech ![]() będzie potokiem pola wektorowego wyznaczonego przez funkcje
będzie potokiem pola wektorowego wyznaczonego przez funkcje ![]() . Nierówność Gronwalla gwarantuje że rozwiązania równania przedłużają się do nieskończoności (dlaczego?), zatem potok jest dobrze określony dla wszystkich
. Nierówność Gronwalla gwarantuje że rozwiązania równania przedłużają się do nieskończoności (dlaczego?), zatem potok jest dobrze określony dla wszystkich ![]() .
.
Sprawdzimy (poniżej) że dyfeomorfizm ![]() spełnia założenia Stwierdzenia 6.1. Istnieje więc homeomorfizm
spełnia założenia Stwierdzenia 6.1. Istnieje więc homeomorfizm ![]() sprzęgający
sprzęgający ![]() z jego częscią liniową
z jego częscią liniową ![]() ;
; ![]() Ten homeomorfizm sprzęga również całe potoki, tzn.
Ten homeomorfizm sprzęga również całe potoki, tzn. ![]() . Aby to sprawdzić, zauważmy że jeśli zdefiniować
. Aby to sprawdzić, zauważmy że jeśli zdefiniować ![]() to
to ![]() jest również sprzężeniem między
jest również sprzężeniem między ![]() z jego częscią liniową
z jego częscią liniową ![]() .
.
Istotnie:
Ale ![]() jest, podobnie jak
jest, podobnie jak ![]() małym (tzn. ograniczonym) zaburzeniem identyczności (pamiętamy że teraz
małym (tzn. ograniczonym) zaburzeniem identyczności (pamiętamy że teraz ![]() jest ustalone):
jest ustalone):
Pierwszy składnik jest ograniczony bo różnica w nawiasie jest równa zero dla argumentów o dużym module. Drugi składnik jest ograniczony bo ![]() jest ograniczone.
Z jedyności sprzężenia w pierwszej, juz udowodnionej części twierdzenia, wynika że
jest ograniczone.
Z jedyności sprzężenia w pierwszej, juz udowodnionej części twierdzenia, wynika że ![]() .
.
Pozostaje więc do sprawdzenia że dyfeomorfizm ![]() spełnia założenia Stwierdzenia 6.1.
Zapisując
spełnia założenia Stwierdzenia 6.1.
Zapisując ![]() , mamy
, mamy
Wiec:
czyli
gdzie ![]() .
Jeśli
.
Jeśli ![]() jest lipschitzowskie z mała stała, to
jest lipschitzowskie z mała stała, to ![]() - też.
- też.
6.3. Twierdzenie Hadamarda-Perrona
Twierdzenie Grobmana -Hartmana gwarantuje istnienie lokalnych zbiorów stabilnych i niestabilnych- są to obrazy przy homeomorfizmie ![]() podprzestrzeni liniowych
podprzestrzeni liniowych ![]() i
i ![]() . Możemy więc wywnioskować że są to topologiczne podrozmaitości.
W istocie- są to podrozmaitości różniczkowalne, tej samej klasy co wyjściowe przekształcenie.
. Możemy więc wywnioskować że są to topologiczne podrozmaitości.
W istocie- są to podrozmaitości różniczkowalne, tej samej klasy co wyjściowe przekształcenie.
Definicja 6.6
Niech ![]() będzie dyfeomorfizmem klasy
będzie dyfeomorfizmem klasy ![]() , określonym na otoczeniu punktu
, określonym na otoczeniu punktu ![]() . Zakładamy że
. Zakładamy że ![]() i że różniczka
i że różniczka ![]() jest hiperbolicznym przekształceniem liniowym.
Dla
jest hiperbolicznym przekształceniem liniowym.
Dla ![]() określamy
określamy
Zbiory te nazywamy- odpowiednio- stabilną i niestabilną lokalną rozmaitością punktu ![]() ,
,
Twierdzenie ponizej uzasadnia nazwę
Twierdzenie 6.2 (Twierdzenie Hadamarda-Perrona)
Niech ![]() będzie dyfeomorfizmem klasy
będzie dyfeomorfizmem klasy ![]() , określonym na otoczeniu punktu
, określonym na otoczeniu punktu ![]() . Zakładamy że
. Zakładamy że ![]() i że różniczka
i że różniczka ![]() jest hiperbolicznym przekształceniem liniowym.
Wówczas, dla małego
jest hiperbolicznym przekształceniem liniowym.
Wówczas, dla małego ![]() , zbiory
, zbiory ![]() i
i ![]() są różniczkowalnymi podrozmaitościami klasy
są różniczkowalnymi podrozmaitościami klasy ![]() .
Przestrzenią styczną do
.
Przestrzenią styczną do ![]() w punkcie
w punkcie ![]() jest
jest ![]() , przestrzenią styczną do
, przestrzenią styczną do ![]() w punkcie
w punkcie ![]() jest
jest ![]() .
.
Ponadto, dla ![]() mamy
mamy ![]() gdy
gdy ![]() ; dla
; dla ![]() mamy
mamy ![]() gdy
gdy ![]()
6.4. Globalne rozmaitości stabilne i niestabilne
Niech teraz ![]() będzie dyfeomorfizmem gładkiej
będzie dyfeomorfizmem gładkiej ![]() - wymiarowej rozmaitości
- wymiarowej rozmaitości ![]() i niech
i niech ![]() będzie punktem stałym hiperbolicznym.
Wówczas istnieją lokalne rozmaitości- stabilna i niestabilna- punktu
będzie punktem stałym hiperbolicznym.
Wówczas istnieją lokalne rozmaitości- stabilna i niestabilna- punktu ![]() . Są to obrazy przy parametryzacji odpowiednich
rozmaitości skonstruowanych dla przedstawienia
. Są to obrazy przy parametryzacji odpowiednich
rozmaitości skonstruowanych dla przedstawienia ![]() w mapie:
w mapie: ![]() .
Są to więc
.
Są to więc ![]() - podrozmaitości
- podrozmaitości ![]() .
.
Definicja 6.7
Globalną rozmaitością stabilną punktu stałego hiperbolicznego nazywamy zbiór
Zatem:
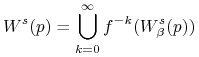 |
Wykażemy
Twierdzenie 6.3
Jeśli ![]() jest hiperbolicznym punktem stałym dla dyfeomorfizmu
jest hiperbolicznym punktem stałym dla dyfeomorfizmu ![]() klasy
klasy ![]() na rozmaitości
na rozmaitości ![]() , to
, to
![]() jest immersyjną podrozmaitością
jest immersyjną podrozmaitością ![]() , klasy
, klasy ![]() .
.
Niech ![]() bedzie parametryzacją otoczenia
bedzie parametryzacją otoczenia ![]() w
w ![]() (już wiemy że
(już wiemy że ![]() jest podrozmaitością).
jest podrozmaitością).
![]() jest zatem określone na otwartym podzbiorze
jest zatem określone na otwartym podzbiorze ![]() ; można założyć że
; można założyć że ![]() .
Różniczka
.
Różniczka ![]() ma rząd
ma rząd ![]() .
Rozpatrzmy
.
Rozpatrzmy
| (6.3) |
Różniczka ![]() ma wszystkie wartości własne mniejsze co do modułu od
ma wszystkie wartości własne mniejsze co do modułu od ![]() (dlaczego?).
Wówczas niekoniecznie norma różniczki
(dlaczego?).
Wówczas niekoniecznie norma różniczki ![]() jest mniejsza niż
jest mniejsza niż ![]() (klatki Jordana!) ale można zmienić normę
w
(klatki Jordana!) ale można zmienić normę
w ![]() , aby to uzyskać (taka zmiana normy była juz w dowodzie twierdzenia Grobmana-Hartmana).
Wówczas istnieje otoczenie zera
, aby to uzyskać (taka zmiana normy była juz w dowodzie twierdzenia Grobmana-Hartmana).
Wówczas istnieje otoczenie zera ![]() takie że dla każdego
takie że dla każdego ![]()
![]() .
.
Ćwiczenie 6.1
Istnieje rozszerzenie przekształcenia ![]() do
do ![]() określonego na całym
określonego na całym ![]() takie że
takie że
![]() jest dyfeomorfizmem
jest dyfeomorfizmem ![]() i
i ![]() .
.
Używając ![]() budujemy immersję
budujemy immersję ![]() , to znaczy różniczkowalne przekształcenie róznowartościowe i takie że w każdym punkcie różniczka ma maksymalny, równy
, to znaczy różniczkowalne przekształcenie róznowartościowe i takie że w każdym punkcie różniczka ma maksymalny, równy ![]() rząd:
rząd:
Ponieważ dla każdego ![]() istnieje
istnieje ![]() takie że
takie że ![]() , rozszerzenie
, rozszerzenie ![]() jest określone dla wszystkich
jest określone dla wszystkich ![]() . Poprawność definicji wynika z określenia
. Poprawność definicji wynika z określenia ![]() (6.3).
(6.3).
Zdefiniujemy teraz rozmaitości stabilne i niestabilne dla elementów krytycznych (tzn. punktów stacjonarnych i orbit zamkniętych) pól wektorowych.
Niech ![]() będzie polem klasy
będzie polem klasy ![]() na gładkiej zwartej rozmaitości
na gładkiej zwartej rozmaitości ![]() , niech
, niech ![]() bedzie potokiem tego pola.
Niech
bedzie potokiem tego pola.
Niech ![]() będzie hiperbolicznym punktem stacjonarnym
będzie hiperbolicznym punktem stacjonarnym ![]() .
.
Definicja 6.8
Globalną rozmaitością stabilną (niestabilną) dla ![]() nazywamy zbiór
nazywamy zbiór
(odpowiednio dla ![]()
![]() ).
).
Twierdzenie 6.4
Przy powyższych założeniach, ![]() ,
, ![]() są immersyjnymi podorozaitościami
są immersyjnymi podorozaitościami ![]() , tej samej klasy co pole wektorowe
, tej samej klasy co pole wektorowe ![]() .
.
Dowód wynika z wykazanego już faktu dla dyfeomorfizmów i z następującego faktu (pozostawiamy udowodnienie jako zadanie)
Ćwiczenie 6.2
Przy założeniach jak powyżej- niech ![]() będzie ”dyfeomorfizmem po czasie
będzie ”dyfeomorfizmem po czasie ![]() dla pola
dla pola ![]() . (Wówczas oczywiście
. (Wówczas oczywiście ![]() i
i ![]() jest punktem stałym hiperbolicznym dla
jest punktem stałym hiperbolicznym dla ![]() ).
Wtedy
).
Wtedy
(i tak samo dla ![]() );
przez
);
przez ![]() oznaczyliśmy globalną rozmaitość stabilną punktu
oznaczyliśmy globalną rozmaitość stabilną punktu ![]() dla
dla ![]() .
.




