Zagadnienia

9.1 Podstawowe definicje i fakty
9.2 Twierdzenie ergodyczne
9.3 Przykłady przekształceń ergodycznych

9. Przekształcenia zachowujące miarę

9.1. Podstawowe definicje i fakty

Rozpatrujemy przestrzeń z miarą probabilistyczną $(X,\mathcal{F},\mu)$ ( $\mathcal{F}$ jest $\sigma$ caiłem zbiorów mierzalnych).

Definicja 9.1

Mówimy że przekształcenie $T:X\to X$ jest mierzalne względem $\sigma$ -ciała $\mathcal{F}$ jeśli dla każdego zbioru $A\in\mathcal{F}$ zbiór $T^{{-1}}(A)$ też należy do $\sigma$ -ciała $\mathcal{F}$ .

Definicja 9.2

Mówimy że mierzalne przekształcenie zachowuje miarę $\mu$ jeśli dla każdego $A\in\mathcal{F}$ mamy

$\mu(T^{{-1}}(A)=\mu(A)$

(9.1)

tu będą przykłady: $z^{2}$ , namiot, $2-z^{2}$ , ułamki łancuchowe

Uwaga 9.1

Jeśli dodatkowo $T$ jest odwracalne i $T^{{-1}}$ jest mierzalne, to warunek 9.1 możemy zapisać

$\mu(T(A)=\mu(A)$

Twierdzenie 9.1 (Twierdzenie Poincare'go o powracaniu)

Niech $(X,\mathcal{F},\mu)$ będzie przestrzenią probablistyczną $T:X\to X$ - zachowuje miarę $\mu$ , $A\in\mathcal{F}$ . Wówczas dla $\mu$ -prawie każdego $x\in A$ istnieje nieskończenie wiele czasów $n$ takich że $T^{n}(x)\in A$ .

Zbiór

$B=\{ x\in A:\exists m>0:\forall n\ge m~~T^{n}(x)\not\in A$

jest mierzalny (dlaczego?). Pokażemy że $\mu(B)=0$ . Wystarczy pokazać że $\mu(C)=0$ gdzie

$C=\{ x\in A:\forall n\ge 1~~T^{n}(x)\not\in A$

Zauważamy że zbiory $C,T^{{-1}}(C),\dots,T^{{-n}}(C)\dots$ są parami rozłaczne. Jest ich nieskończenie wiele, miara $X$ jest skończona, Zatemu wszystkie te zbiory muszą mieć miarę zero.

∎

Podamy teraz ważną definicję:

Definicja 9.3 (Ergodyczność)

Przekształcenie mierzalne przestrzeni z miarą $X$ nazywamy ergodycznym jeśli dla każdego $A$ zbioru mierzalnego mamy

$\mu(A\div T^{{-1}}(A))=0\implies\mu(A)=0~~{\rm lub}~~\mu(X\setminus A)=0$

Uwaga 9.2

W tej definicji ergodyczności nie zakłądamy ani niezmienniczości miary $\mu$ dla przekształcenia $T$ ani skończoności miary $\mu$ . Jeśli $T$ dodatkowo spełnia implikację $\mu(A)=0\implies\mu(T^{{-1}}(A)=0$ , w szczególności jeśli $T$ zachowuje miarę $\mu$ to definicję ergodyczności można równoważnie zapisać (taką definicję spotyka się na ogół)

Definicja 9.4 (Ergodyczność miary niezmienniczej)

Przekształcenie mierzalne $T$ przestrzeni z miarą $X$ , zachowujące tę miarę jest ergodyczne jeśli dla każdego $A$ zbioru mierzalnego mamy

$A=T^{{-1}}(A)\implies\mu(A)=0~~{\rm lub}~~\mu(X\setminus A)=0$

Zdefiniujemy teraz $\sigma$ -ciało zbiorów ”prawie” niezmienniczych

$\mathcal{G}=\{ A\in\mathcal{F}:\mu(A\div T^{{-1}}(A))=0$

Mamy łatwe

Stwierdzenie 9.1

Jeśli funkcja $\phi:X\to\mathbb{R}$ jest mierzalna względem $\sigma$ -ciała $\mathcal{G}$ to $\phi$ jest prawie na pewno stała na trajektoriach:

$\mu\{ x:\phi(Tx)=\phi(x)\}=1$

. Załóżmy przeciwnie, że $D=\{ x:\phi(Tx)\neq\phi(x)\}$ ma dodatnią miarę. Wówczas istnieje takie $a\in\mathbb{Q}$ że zbiór $D_{a}=\{ x\in D:\phi(x)<a~{\rm i}~\phi(Tx)>a\}$ ma dodatnią miarę (albo dodatnią miarę ma zbiór $D_{a}$ zdefiniowany przez przeciwne nierówności). Ale $D_{a}$ nie przecina się z $T^{{-1}}(D_{a})$ (wystarczy spojrzeć na definicję zbioru $D_{a}$ ); z drugiej strony $D_{a}$ jest elementem $\sigma$ ciała $\mathcal{G}$ . Wynika stąd że $\mu(D_{a})=0$ , wbrew przypuszczeniu (zbiory z $\sigma$ -ciała $\mathcal{G}$ różnią się przecież od swojego przeciwobrazu o zbiór miary zero).

∎

Zanotujmy jeszcze oczywiste ale ważne fakty:

Stwierdzenie 9.2

Jesłi $T:X\to X$ jest przekształceniem zachowujacym miarę, to $T$ jest ergodyczne wtedy i tylko wtedy gdy $\sigma$ - ciało $\mathcal{G}$ jest trywialne (składa się wyłącznie ze zbiorów miary $0$ i zbiorów miary $1$ ).

Wniosek 9.1

Jeśli $T:X\to X$ jest ergodyczne, to każda funkcja mierzalna $\phi:X\to\mathbb{R}$ która jest $T$ - niezmiennicza (tzn $\phi\circ T=\phi$ prawie wszędzie) jest stałą prawie wszędzie.

Gdzies troszke dalej w forma zadania moze, trzeba umiescic różne warunki równoważne na ergodyczność

9.2. Twierdzenie ergodyczne

Twierdzenie Ergodyczne jest jednym z najważniejszych wyników w teorii przekształceń zachowujących miarę. Rozważmy funkcję mierzalną $\phi:X\to\mathbb{R}$ (czyli - w języku rachunku prawdopodobieństwa- zmienną losową). Mamy wówczas ciąg funkcji mierzalnych (zmiennych losowych)

$\phi,\phi\circ T,\phi\circ T^{2},\dots,\phi\circ T^{n},\dots$

(9.2)

(mamy więc jakąs funkcję (obserwablę) określoną na naszej przestrzeni $X$ i wyliczamy jej wartości wzdłuż trajektorii).

Otrzymujemy w ten sposób ciąg zmiennych losowych o tym samym rozkłądzie (dlaczego?), ale oczywiscie nie niezależnych. Twierdzenie Ergodyczne jest odpowiednikiem Prawa Wielkich Liczb, dla takiego właśnie ciągu jednakowo rozlożonych i całkowalnych ale zależnych (przez sposób w jaki zostały zdefiniowane) zmiennych losowych.

Twierdzenie 9.2 (Twierdzenie Ergodyczne)

Niech $T:X\to X$ będzie przekształceniem zachowującym miarę probabilistyczną $\mu$ określoną na $\sigma$ ciele $\mathcal{F}$ podzbiorów $X$ . Niech $\phi:X\to\mathbb{R}$ będzie funkcją całkowalną względem miary $\mu$ ( $\phi\in L^{1}(\mu)$ ). Wówczas mamy

${{\phi+\phi\circ T+\phi\circ T^{2}+\dots+\phi\circ T^{{n-1}}}\over{n}}\to E(\phi|\mathcal{G})$

(9.3)

(gdzie $E(\phi|\mathcal{G}$ oznacza warunkową wartość oczekiwaną względem $\sigma$ - ciała $\mathcal{G}$ ). Zbieżność jest tutaj prawie wszędzie i w $L^{1}$ .

Uwaga 9.3

Zauważmy że (jak wynika ze Stwierdzenia 9.1) funkcja $E(\phi|\mathcal{G}$ jest (prawie wszędzie) $T$ - niezmiennicza. Zatem w twierdzieniu ergodycznym otzymujemy zbieżność do funcji $T$ - niezmienniczej, oczywiscie o tej samej całce co $\phi$ .

Wniosek 9.2

Jeśli dodatkowo założymy że $T$ jest ergodyczne, mamy

${{\phi+\phi\circ T+\phi\circ T^{2}+\dots+\phi\circ T^{{n-1}}}\over{n}}\to E(\phi)$

(9.4)

prawie wszędzie (zatem dla ergodycznego przekształcenia $T$ teza twierdzenia jest dokładnym odpowiednikiem Prawa Wielkich Liczb).

Wniosek 9.3 (Częstość odwiedzin)

Jesli $T:X\to X$ jest ergodyczne, $A\in\mathcal{F}$ to z Twierdzenia Ergodycznego, zastosowanego dla $\phi=\xi _{A}$ otrzymujemy

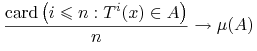${{{\rm card}\left(i\le n:T^{i}(x)\in A\right)}\over n}\to\mu(A)$

(9.5)

prawie wszędzie.

Dowód Twierdzenia Ergodycznego

Najpierw udowodnimy następujący Lemat:

Lemat 9.1 (Maksymalne Twierdzenie Ergodyczne)

Niech $f\in L^{{1}}(\mu)$ . Zdefiniujmy zbiór $A$ następująco:

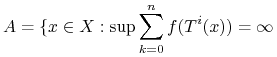$A=\{ x\in X:\sup\sum _{{k=0}}^{n}f(T^{i}(x))=\infty$

Wówczas

$\int _{A}f\ge 0$

Określamy

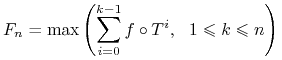$F_{n}=\max\left(\sum _{{i=0}}^{{k-1}}f\circ T^{i},~~1\le k\le n\right)$

(9.6)

Zauważmy że

$F^{{n+1}}(x)-F^{n}(Tx)=f(x)-\min\left(0,F_{n}(Tx)\right)$

(9.7)

Wynika stąd po pierwsze że ciąg $F^{{n+1}}(x)-F^{n}(Tx)$ jest nierosnący, a po drugie- że dla $x\in A$ mamy

$F_{{n+1}}(x)-F_{n}(Tx)\to f(x)$

(9.8)

a stąd:

$0\le\int _{A}\left(F_{{n+1}}-F_{n}\right)d\mu=\int _{A}\left(F_{{n+1}}-F_{n}\circ T\right)\to\int _{A}fd\mu$

(9.9)

Równość wynika stąd że z niezmienniczości miary $\mu$ mamy $\int _{{f^{{-1}}(A)}}F_{n}\circ T=\int _{A}F_{n}$ , a dzięki temu że zbiór $A$ jest niezmienniczy ( $A$ ( $f^{{-1}}(A)=A$ ), możemy następnie $f^{{-1}}(A)$ zastąpić przez $A$ .

Ostatnie przejscie do granicy jest uprawnione, bo ciąg funkcji $F_{{n+1}}-F_{n}\circ T$ jest nierosnący, i zbieżny na zbiorze $A$ do całkowalnej funkcji $f$ . Formuła LABEL:max kończy dowód Maksymalnego Twierdzenia Ergodycznego.

∎

Założmy teraz że $E(f|\mathcal{G})<0$ prawie wszędzie. Skoro $A$ jest niezmienniczy, to oczywiście $A\in\mathcal{G}$ , zatem

$\int _{A}f=\int _{A}E(f|\mathcal{G})<0$

Zatem: jeśli $E(f|\mathcal{G})<0$ prawie wszędzie, to z Maksymalnego Twierdzenia Ergodycznego wynika że $\mu(A)=0$ . Poza zbiorem $A$ mamy zaś oczywiście:

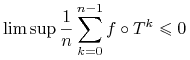$\limsup{1\over n}\sum _{{k=0}}^{{n-1}}f\circ T^{k}\le 0$

(9.10)

Zastosujemy tę obserwację do funkcji

$f=\phi-E(\phi|\mathcal{G})-\varepsilon$

( $\varepsilon$ jest tu dowolną liczbą dodatnią). Oczywiście $E(f|\mathcal{G})=-\varepsilon<0$

Mamy zatem

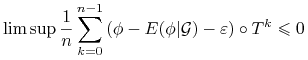$\limsup{1\over n}\sum _{{k=0}}^{{n-1}}\left(\phi-E(\phi|\mathcal{G})-\varepsilon\right)\circ T^{k}\le 0$

(9.11)

Stwierdzenie refniezm pozwala teraz zauważyć że funkcja $E(\phi|\mathcal{G})$ jest $T$ - niezmiennicza, zatem nierówność 9.11 możemy (prawie wszędzie) przepisac:

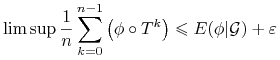$\limsup{1\over n}\sum _{{k=0}}^{{n-1}}\left(\phi\circ T^{k}\right)\le E(\phi|\mathcal{G})+\varepsilon$

(9.12)

Dla zakończenia dowodu wystarczy teraz zauważyć że $\varepsilon$ jest dowolne, zatem

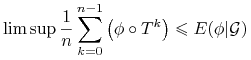$\limsup{1\over n}\sum _{{k=0}}^{{n-1}}\left(\phi\circ T^{k}\right)\le E(\phi|\mathcal{G})$

prawie wszędzie (wystarczy wybrać ciąg epsylonów zbieżny do zera), zaś zamieniając $\phi$ na $-\phi$ otrzymujemy:

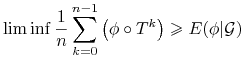$\liminf{1\over n}\sum _{{k=0}}^{{n-1}}\left(\phi\circ T^{k}\right)\ge E(\phi|\mathcal{G})$

Pozostaje do sprawdzenia że zbieżność jest także w $L^{1}$

∎

Sformułujemy teraz kilka warunków równoważnych ergodyczności; pozostawimy je jako zadanie:

Ćwiczenie 9.1 (Warunki równoważne ergodyczności)

Niech $T:X\to X$ będzie przekształceniem zachowującym miarę $\mu$ . Wykazać równoważność następujących warunków:

1. 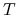$T$ jest ergodyczne
2. każda funkcja 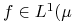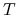$f\in L^{1}(\mu$ , $T$ - niezmiennicza jest stała prawie wszędzie.
2'. każda funkcja 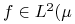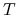$f\in L^{2}(\mu$ , $T$ - niezmiennicza jest stała prawie wszędzie.
3. dla każdej funkcji 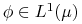$\phi\in L^{{1}}(\mu)$ mamy

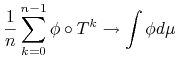
${1\over n}\sum _{{k=0}}^{{n-1}}\phi\circ T^{k}\to\int\phi d\mu$
3'. dla każdego zbioru 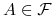$A\in\mathcal{F}$ mamy

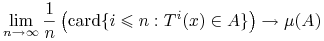
$\lim _{{n\to\infty}}{1\over n}\left({\rm card}\{ i\le n:T^{i}(x)\in A\}\right)\to\mu(A)$

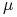$\mu$ - prawie wszędzie.
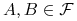
4. dla dowolnych zbiorów $A,B\in\mathcal{F}$

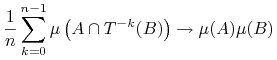
${1\over n}\sum _{{k=0}}^{{n-1}}\mu\left(A\cap T^{{-k}}(B)\right)\to\mu(A)\mu(B)$

Następne ćwiczenie pokazuje że dla tego samego przekształcenia miary ergodyczne niezmiennicze są dla siebie ”wzajemnie niewidoczne”.

Ćwiczenie 9.2

NIech $T:X\to X$ będzie przekształceniem mierzalnym względem $\sigma$ -ciała $\mathcal{F}$ . Wykazać że jeśli $\mu _{1}$ , $\mu _{2}$ są dwiema różnymi miarami określonymi na $\mathcal{F}$ , to $\mu _{1}$ , $\mu _{2}$ są wzajemnie singularne.

Wskazówka:

Skoro miary są rózne, to istnieje $A\in\mathcal{F}$ taki że $\mu _{1}(A)\neq\mu _{2}(A)$ . Skorzystać z własności $3^{{\prime}}$ z poprzedniego zadania.

9.3. Przykłady przekształceń ergodycznych

obrot na okręgu, przesunięcia na torusie, automorfizmy torusa, układy symboliczne

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.