Zagadnienia

1.1 Podstawowe definicje
1.2 Proces Wienera (ruch Browna)
1.3 Charakteryzacje procesu Wienera
1.4 Uwagi i uzupełnienia
- 1.4.1 Konstrukcja Procesu Wienera
- 1.4.2 Nieróżniczkowalność trajektorii
1.5 Zadania

1. Procesy stochastyczne. Proces Wienera

Podczas pierwszego wykładu określimy czym jest proces stochastyczny oraz zdefiniujemy proces Wienera – najważniejszy przykład procesu o ciągłych trajektoriach.

1.1. Podstawowe definicje

Zaczniemy od podania ważnych definicji używanych podczas całego wykładu.

Definicja 1.1

Niech $(\Omega,{\mathcal{F}},{\mathbb{P}})$ będzie przestrzenią probabilistyczną, $(E,{\mathcal{E}})$ przestrzenią mierzalną, zaś $T$ dowolnym zbiorem. Procesem stochastycznym o wartościach w $E$ , określonym na zbiorze $T$ , nazywamy rodzinę zmiennych losowych $X=(X_{{t}})_{{t\in T}}$ , przyjmujących wartości w zbiorze $E$ .

Uwaga 1.1

W czasie wszystkich dalszych wykładów $T$ będzie podzbiorem ${\mathbb{R}}$ (najczęściej przedziałem, niekoniecznie ograniczonym), zaś $E={\mathbb{R}}$ lub ${\mathbb{R}}^{{d}}$ . Parametr $t$ można wówczas interpretować jako czas.

Definicja 1.2

Trajektorią procesu $X$ nazywamy funkcję (losową!) $t\rightarrow X_{{t}}(\omega)$ , określoną na zbiorze $T$ o wartościach w $E$ .

Definicja 1.3

Powiemy, że proces $X=(X_{{t}})_{{t\in T}}$ , $T\subset{\mathbb{R}}$ ma przyrosty niezależne jeśli dla dowolnych indeksów $t_{{0}}\leq t_{{1}}\leq\ldots\leq t_{{n}}$ ze zbioru $T$ , zmienne losowe $X_{{t_{{0}}}},X_{{t_{{1}}}}-X_{{t_{{0}}}},X_{{t_{{2}}}}-X_{{t_{{1}}}},\ldots,X_{{t_{{n}}}}-X_{{t_{{n-1}}}}$ są niezależne.

Definicja 1.4

Mówimy, że proces stochastyczny $(X_{{t}})_{{t\geq 0}}$ ma przyrosty stacjonarne, jeśli rozkład $X_{{t}}-X_{{s}}$ zależy tylko od $t-s$ , czyli

$\forall _{{t>s\geq 0}}\ X_{{t}}-X_{{s}}\sim X_{{t-s}}-X_{{0}}.$

1.2. Proces Wienera (ruch Browna)

Definicja 1.5

Procesem Wienera (ruchem Browna) nazywamy proces stochastyczny $W=(W_{{t}})_{{t\geq 0}}$ taki, że

		$\displaystyle W_{{0}}=0\mbox{ p.n.};$
		$\displaystyle W\mbox{ ma przyrosty niezależne};$
		$\displaystyle\mbox{Dla $0\leq s<t$ zmienna $W_{{t}}-W_{{s}}$ ma rozkład normalny ${\mathcal{N}}(0,t-s)$};$
		Trajektorie $W$ są ciągłe z prawdopodobieństwem 1.

Uwaga 1.2

Warunek (W3) oznacza, że istnieje zbiór $A$ taki, że ${\mathbb{P}}(A)=1$ oraz dla wszystkich $\omega\in A$ , $t\rightarrow W_{{t}}(\omega)$ jest funkcją ciągłą na $[0,\infty)$ . Czasami w definicji procesu Wienera zakłada się, że wszystkie trajektorie są ciągłe oraz $W_{0}\equiv 0$ .

1.3. Charakteryzacje procesu Wienera

Najpierw podamy twierdzenie, które znacznie ułatwia sprawdzanie, że dany proces jest procesem Wienera. Musimy wpierw podać ważną definicję.

Definicja 1.6

Proces $X=(X_{{t}})_{{t\in T}}$ nazywamy gaussowskim, jeśli wszystkie skończenie wymiarowe rozkłady $X$ są gaussowskie, tzn. wektor $(X_{{t_{{1}}}},\ldots,X_{{t_{{n}}}})$ ma rozkład gaussowski dla dowolnych $t_{{1}},\ldots,t_{{n}}\in T$ .

Przykład 1.1

Następujące procesy są procesami gaussowskimi:

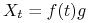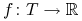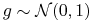$X_{{t}}=f(t)g$ , gdzie $f\colon T\rightarrow{\mathbb{R}}$ dowolne oraz $g\sim{\mathcal{N}}(0,1)$ ,
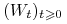proces Wienera $(W_{{t}})_{{t\geq 0}}$ ,
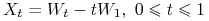most Browna $X_{{t}}=W_{{t}}-tW_{{1}},\ 0\leq t\leq 1$ .

Przykład 1.2

Procesy $(W_{t}^{2})_{{t\geq 0}}$ , $(\exp(W_{t}))_{{t\geq 0}}$ nie są gaussowskie.

Twierdzenie 1.1

Proces $(X_{{t}})_{{t\geq 0}}$ jest procesem Wienera wtedy i tylko wtedy, gdy jest procesem gaussowskim, o ciągłych trajektoriach p.n. takim, że ${\mathbb{E}}X_{t}=0$ oraz $\mathrm{Cov}(X_{t},X_{s})=\min\{ t,s\}$ .

$\Rightarrow$ : Mamy ${\mathbb{E}}X_{t}={\mathbb{E}}(X_{t}-X_{0})=0$ oraz $\mathrm{Var}(X_{t})=\mathrm{Var}(X_{t}-X_{0})=t$ na mocy (W0) i (W2). Ponadto z niezależności przyrostów, dla $t\geq s$ , $\mathrm{Cov}(X_{t},X_{s})=\mathrm{Cov}(X_{t}-X_{s},X_{s})+\mathrm{Var}(X_{s})=0+s=\min\{ t,s\}$ .

$\Leftarrow$ : Zauważmy, że $\mathrm{Var}(X_{0})=0={\mathbb{E}}X_{0}$ , więc spełniony jest warunek (W0). Dla $t>s$ , zmienna $W_{t}-W_{s}$ ma rozkład normalny ze średnią $0$ i wariancją $\mathrm{Var}(X_{t}-X_{s})=\mathrm{Var}(X_{t})+\mathrm{Var}(X_{s})-2\mathrm{Cov}(X_{t},X_{s})=t-s$ , więc zachodzi (W2). By sprawdzić niezależność przyrostów ustalmy $0\leq t_{0}\leq t_{1}\leq\ldots\leq t_{n}$ . Zauważmy, że wektor $(X_{{t_{0}}},X_{{t_{{1}}}}-X_{{t_{{0}}}},X_{{t_{{2}}}}-X_{{t_{{1}}}},\ldots,X_{{t_{{n}}}}-X_{{t_{{n-1}}}})$ ma rozkład gaussowski, więc jego współrzędne są niezależne wtedy i tylko wtedy, gdy są nieskorelowane. Mamy jednak dla $s_{1}\leq s_{2}\leq s_{3}\leq s_{4}$ ,

$\mathrm{Cov}(X_{{s_{1}}},X_{{s_{3}}}-X_{{s_{2}}})=\mathrm{Cov}(X_{{s_{1}}},X_{{s_{3}}})-\mathrm{Cov}(X_{{s_{1}}},X_{{s_{2}}})=s_{1}-s_{1}=0$

oraz

$\mathrm{Cov}(X_{{s_{2}}}-X_{{s_{1}}},X_{{s_{4}}}-X_{{s_{3}}})=\mathrm{Cov}(X_{{s_{2}}},X_{{s_{4}}}-X_{{s_{3}}})-\mathrm{Cov}(X_{{s_{1}}},X_{{s_{4}}}-X_{{s_{3}}})=0.$

∎

Kolejne twierdzenie pokazuje, że (z dokładnością do drobnych technicznych założeń oraz normalizacji) proces Wienera jest jedynym procesem o ciągłych trajektoriach oraz niezależnych i stacjonarnych przyrostach.

Twierdzenie 1.2

Załóżmy, że proces $(X_{{t}})_{{t\geq 0}}$ spełnia warunki (W0), (W1), (W3) (z $W$ zastąpionym przez $X$ ) oraz

		$\displaystyle X\mbox{ ma przyrosty stacjonarne};$
		$\displaystyle{\mathbb{E}}X_{{1}}=0,\ \mathrm{Var}(X_{{1}})=1;$
		$\displaystyle{\mathbb{E}}X_{{t}}^{{4}}<\infty\mbox{ dla wszystkich }t>0.$

Wówczas $X_{{t}}$ jest procesem Wienera.

Określmy dla $t\geq 0$ , $a(t)={\mathbb{E}}X_{t}$ oraz $b(t)=\mathrm{Var}(X_{t})$ . Zauważmy, że na mocy niezależności i stacjonarności przyrostów,

	$\displaystyle b(t+s)$	$\displaystyle=\mathrm{Var}(X_{{t+s}}-X_{t}+X_{t})=\mathrm{Var}(X_{{t+s}}-X_{t})+\mathrm{Var}(X_{t})$
		$\displaystyle=\mathrm{Var}(X_{s})+\mathrm{Var}(X_{t})=b(t)+b(s).$

Ponadto oczywiście $b(t)\geq 0$ , zatem funkcja $b(t)$ jest addytywna i niemalejąca na $[0,\infty)$ , więc $b(t)=ct$ dla pewnego $c\geq 0$ , co wobec (W2b) daje $\mathrm{Var}(X_{t})=b(t)=t$ . Analogicznie sprawdzamy, że $a(t+s)=a(t)+a(s)$ , wiemy też, że $a(0)=1$ , stąd wnioskujemy, że ${\mathbb{E}}X_{t}=a(t)=0$ dla $t$ wymiernych. Weźmy $t>0$ i wybierzmy dążący do $t$ ciąg liczb wymiernych $(t_{n})$ . Na mocy (W2c), ${\mathbb{E}}X_{t}^{2}<\infty$ , wiemy też, że ${\mathbb{E}}X_{{t_{n}}}^{2}=\mathrm{Var}(X_{{t_{n}}})=t_{n}$ , zatem $({\mathbb{E}}|X_{{t_{n}}}-X_{t}|^{2})^{{1/2}}\leq M$ dla pewnej stałej $M$ . Z ciągłości trajektorii $X_{{t_{n}}}\rightarrow X_{t}$ prawie na pewno, czyli również według prawdopodobieństwa. Zatem dla $\varepsilon>0$ ,

	$\displaystyle\|{\mathbb{E}}X_{t}\|$	$\displaystyle=\|{\mathbb{E}}X_{t}-{\mathbb{E}}X_{{t_{n}}}\|\leq{\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|\leq\varepsilon+{\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|{\mathrm{I}}_{{\{\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon\}}}$
		$\displaystyle\leq\varepsilon+({\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|^{2})^{{1/2}}{\mathbb{P}}(\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon)^{{1/2}}$
		$\displaystyle\leq\varepsilon+M{\mathbb{P}}(\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon)^{{1/2}}\leq 2\varepsilon$

dla dostatecznie dużych $n$ . Stąd ${\mathbb{E}}X_{t}=0$ . Wykazaliśmy więc, że $X_{t}$ ma średnią zero i wariancję $t$ .

Ustalmy $t>s\geq 0$ , chcemy pokazać, że $X_{t}-X_{s}$ ma rozkład normalny ${\mathcal{N}}(0,t-s)$ . Zauważmy, że

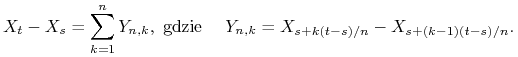$X_{{t}}-X_{s}=\sum _{{k=1}}^{{n}}Y_{{n,k}},\mbox{ gdzie }\quad Y_{{n,k}}=X_{{s+k(t-s)/n}}-X_{{s+(k-1)(t-s)/n}}.$

Zmienne $(Y_{{n,k}})_{{1\leq k\leq n}}$ tworzą układ trójkątny, możemy więc skorzystać z Centralnego Twierdzenia Granicznego i wykazać, że $\sum _{{k=1}}^{n}Y_{{n,k}}$ zbiega do ${\mathcal{N}}(0,t-s)$ według rozkładu. Mamy

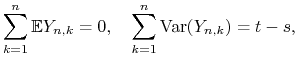$\sum _{{k=1}}^{n}{\mathbb{E}}Y_{{n,k}}=0,\quad\sum _{{k=1}}^{n}\mathrm{Var}(Y_{{n,k}})=t-s,$

wystarczy więc sprawdzić warunek Lindeberga. Dla $\varepsilon>0$ ,

	$\displaystyle L_{n}(\varepsilon)$	$\displaystyle=\sum _{{k=1}}^{n}{\mathbb{E}}\|Y_{{n,k}}\|^{2}{\mathrm{I}}_{{\{\|Y_{{n,k}}\|\geq\varepsilon\}}}\leq{\mathbb{E}}\Big[\Big(\sum _{{k=1}}^{n}\|Y_{{n,k}}\|^{2}\Big){\mathrm{I}}_{{\{\max _{{k\leq n}}\|Y_{{n,k}}\|\geq\varepsilon\}}}\Big]$
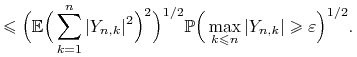		$\displaystyle\leq\Big({\mathbb{E}}\Big(\sum _{{k=1}}^{n}\|Y_{{n,k}}\|^{2}\Big)^{2}\Big)^{{1/2}}{\mathbb{P}}\Big(\max _{{k\leq n}}\|Y_{{n,k}}\|\geq\varepsilon\Big)^{{1/2}}.$

Zauważmy, że zmienne $(Y_{{n,k}})$ dla ustalonego $n$ są niezależne i mają średnią zero, zatem

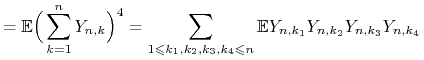	$\displaystyle{\mathbb{E}}(X_{t}-X_{s})^{4}$	$\displaystyle={\mathbb{E}}\Big(\sum _{{k=1}}^{{n}}Y_{{n,k}}\Big)^{4}=\sum _{{1\leq k_{1},k_{2},k_{3},k_{4}\leq n}}{\mathbb{E}}Y_{{n,k_{1}}}Y_{{n,k_{2}}}Y_{{n,k_{3}}}Y_{{n,k_{4}}}$
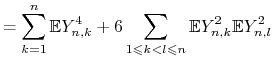		$\displaystyle=\sum _{{k=1}}^{n}{\mathbb{E}}Y_{{n,k}}^{4}+6\sum _{{1\leq k<l\leq n}}{\mathbb{E}}Y_{{n,k}}^{2}{\mathbb{E}}Y_{{n,l}}^{2}$
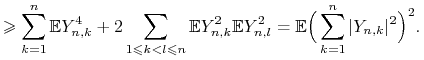		$\displaystyle\geq\sum _{{k=1}}^{n}{\mathbb{E}}Y_{{n,k}}^{4}+2\sum _{{1\leq k<l\leq n}}{\mathbb{E}}Y_{{n,k}}^{2}{\mathbb{E}}Y_{{n,l}}^{2}={\mathbb{E}}\Big(\sum _{{k=1}}^{n}\|Y_{{n,k}}\|^{2}\Big)^{2}.$

Z ciągłości trajektorii $X$ wynika, że ${\mathbb{P}}(\max _{{k\leq n}}|Y_{{n,k}}|\geq\varepsilon)\rightarrow 0$ przy $n\rightarrow\infty$ , zatem spełniony jest warunek Lindeberga $\lim _{{n\rightarrow\infty}}L_{n}(\varepsilon)=0$ .

∎

Uwaga 1.3

Warunek (W2c) nie jest konieczny - zob. Twierdzenie 5 z paragrafu 13.1 książki [3].

Okazuje się, że również nie trzeba zakładać skończoności wariancji ani nawet istnienia wartości średniej $W_{{1}}$ - warunek (W2b) ma charakter czysto normalizacyjny. Dokładniej zachodzi następujące twierdzenie.

Twierdzenie 1.3

Załóżmy, że proces stochastyczny $X=(X_{{t}})_{{t\geq 0}}$ spełnia warunki (W0),(W1), (W2a) i (W3). Wówczas istnieją stałe $a,b\in{\mathbb{R}}$ i proces Wienera $W$ takie, że $X_{{t}}=aW_{{t}}+bt$ dla wszystkich $t\geq 0$ .

1.4. Uwagi i uzupełnienia

1.4.1. Konstrukcja Procesu Wienera

Podczas następnych wykładów podamy dość abstrakcyjną konstrukcję procesu Wienera opartą o ogólniejsze twierdzenia dotyczące istnienia i ciągłości trajektorii procesów stochastycznych. Alternatywna, bardziej bezpośrednia konstrukcja (wymagająca pewnej znajomości analizy funkcjonalnej) procesu Wienera jest zawarta w Ćwiczeniach 1.10-1.12.

1.4.2. Nieróżniczkowalność trajektorii

Trajektorie procesu Wienera mają wiele ciekawych własności, jedną z nich jest to, że prawdopodobieństwem 1 są funkcjami ciągłymi, nieróżniczkowalnymi w żadnym punkcie.

Twierdzenie 1.4

Prawie wszystkie trajektorie procesu Wienera $(W_{{t}})_{{t\geq 0}}$ są funkcjami nieróżniczkowalnymi w żadnym punkcie, tzn.

${\mathbb{P}}\Big(\exists _{{t_{{0}}\geq 0}}\ t\rightarrow W_{{t}}(\omega)\mbox{ jest różniczkowalne w }t_{{0}}\Big)=0.$

1.5. Zadania

Ćwiczenie 1.1

Znajdź rozkład zmiennej $5W_{1}-W_{3}+W_{7}$ .

Ćwiczenie 1.2

Dla jakich parametrów $a$ i $b$ , zmienne $aW_{1}-W_{2}$ oraz $W_{3}+bW_{5}$ są niezależne?

Ćwiczenie 1.3

Udowodnij, że $\lim _{{t\rightarrow\infty}}\frac{W_{{t}}}{t}=0$ p.n.

Ćwiczenie 1.4

Znajdź rozkład wektora losowego $(W_{{t_{{1}}}},W_{{t_{{2}}}},\ldots,W_{{t_{{n}}}})$ dla $0<t_{{1}}<t_{{2}}<\ldots<t_{{n}}$ .

Ćwiczenie 1.5

Udowodnij, że z prawdopodobieństwem $1$ trajektorie procesu Wienera są nieograniczone.

Ćwiczenie 1.6

Udowodnij, że z prawdopodobieństwem $1$ trajektorie procesu Wienera nie są jednostajnie ciągłe na ${\mathbb{R}}_{+}$ .

Ćwiczenie 1.7

Udowodnij, że następujące procesy też są procesami Wienera:
i) $X_{{t}}=-W_{{t}}$ (odbicie);
ii) $Y_{{t}}=c^{{-1/2}}W_{{ct}},c>0$ (przeskalowanie czasu);
iii) $Z_{{t}}=tW_{{1/t}}$ dla $t>0$ oraz $Z_{{0}}=0$ (inwersja czasu);
iv) $U_{{t}}=W_{{T+t}}-W_{{T}},T\geq 0$ ;
v) $V_{{t}}=W_{{t}}$ dla $t\leq T$ , $V_{{t}}=2W_{{T}}-W_{{t}}$ dla $t>T$ , gdzie $T\geq 0$ .

Ćwiczenie 1.8

Niech $\pi _{{n}}=\{ t_{{0}}^{{(n)}},t_{{1}}^{{(n)}},\ldots,t_{{k_{n}}}^{{(n)}}\}$ , gdzie $a=t_{{0}}^{{(n)}}<t_{{1}}^{{(n)}}<\ldots<t_{{k_{n}}}^{{(n)}}=b$ będzie ciągiem podziałów odcinka $[a,b]$ oraz $\|\pi _{{n}}\|=\max _{{k}}|t_{{k}}^{{(n)}}-t_{{k-1}}^{{(n)}}|$ oznacza średnicę $\pi _{{n}}$ . Udowodnij, że

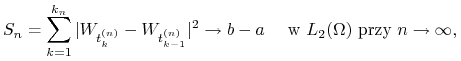$S_{{n}}=\sum _{{k=1}}^{{k_{{n}}}}|W_{{t_{{k}}^{{(n)}}}}-W_{{t_{{k-1}}^{{(n)}}}}|^{{2}}\rightarrow b-a\quad\mbox{ w }L_{{2}}(\Omega)\mbox{ przy }n\rightarrow\infty,$

jeśli $\|\pi _{{n}}\|\rightarrow 0$ oraz $S_{{n}}\rightarrow b-a$ p.n., jeśli $\sum _{{n}}\|\pi _{{n}}\|<\infty$ .

Ćwiczenie 1.9

Udowodnij, że prawie wszystkie trajektorie procesu Wienera mają nieskończone wahanie na każdym przedziale.

Ćwiczenie 1.10

Niech $f_{i}(t)$ będzie dowolną bazą $L_{{2}}[0,1]$ , $h_{i}(t)=\int _{0}^{t}f_{i}(s)ds$ oraz niech $g_{i}$ będzie ciągiem niezależnych zmiennych ${\cal N}(0,1)$ . Wykaż, że szereg $X_{t}=\sum _{{i}}g_{i}h_{i}(t)$ jest zbieżny w $L^{2}$ dla dowolnego $t\in[0,1]$ oraz $X_{t}$ ma te same rozkłady skończenie wymiarowe co proces Wienera.

Ćwiczenie 1.11

Niech $I(0)=\{ 1\},I(n)=\{ 1,\ldots,2^{{n-1}}\},n=1,2,\ldots$ . Układem Haara nazywamy rodzinę funkcji $(h_{{n,k}})_{{n=0,1,\ldots,k\in I(n)}}$ określonych na $[0,1]$ wzorami $h_{{0,1}}(t)\equiv 1$ oraz dla $n=1,2,\ldots,k\in I(n)$ ,

$h_{{n,k}}(t)=\left\{\begin{array}[]{ll}2^{{\frac{n-1}{2}}}&(2k-2)2^{{-n}}\leq t<(2k-1)2^{{-n}},\\ -2^{{\frac{n-1}{2}}}&(2k-1)2^{{-n}}\leq t<2k2^{{-n}},\\ 0&\mbox{w pozostałych przypadkach.}\end{array}\right.$

Układem Schaudera nazywamy rodzinę funkcji $(S_{{n,k}})_{{n=0,1,\ldots,k\in I(n)}}$ określonych na $[0,1]$ wzorem $S_{{n,k}}(t)=\int _{{0}}^{{t}}h_{{n,k}}(s)ds$ . Niech $(g_{{n,k}})_{{n=0,1,\ldots,k\in I(n)}}$ będzie rodziną niezależnych zmiennych losowych o rozkładzie ${\mathcal{N}}(0,1)$ , połóżmy

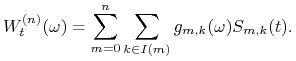$W_{{t}}^{{(n)}}(\omega)=\sum _{{m=0}}^{{n}}\sum _{{k\in I(m)}}g_{{m,k}}(\omega)S_{{m,k}}(t).$

Wykaż, że dla prawie wszystkich $\omega\in\Omega$ ciąg funkcji $(W_{{t}}^{{(n)}}(\omega))$ zbiega jednostajnie na $[0,1]$ do pewnej funkcji ciągłej $W_{{t}}(\omega)$ . Jeśli określimy np. $W_{{t}}(\omega)=0$ dla pozostałych $\omega$ to tak zdefiniowany proces stochastyczny jest procesem Wienera na $[0,1]$ .

Ćwiczenie 1.12

Niech $(W_{{t}})_{{t\in[0,1]}}$ będzie procesem Wienera na $[0,1]$ . Wykaż, że $((1+t)W_{{\frac{1}{1+t}}}-W_{{1}})_{{t\geq 0}}$ jest procesem Wienera na całej półprostej.

Ćwiczenie 1.13

Udowodnij Twierdzenie 1.4.

Wskazówka:

Wykaż wpierw, że jeśli funkcja $f$ jest różniczkowalna w jakimś punkcie przedziału $[0,1)$ , to

$\exists _{{M<\infty}}\ \exists _{{m<\infty}}\ \forall _{{n\geq m}}\ \exists _{{0\leq j\leq n-3}}\ \forall _{{k=0,1,2}}\ \Big|f\Big(\frac{j+k+1}{n}\Big)-f\Big(\frac{j+k}{n}\Big)\Big|\leq\frac{5M}{n}.$

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

	$\displaystyle\|{\mathbb{E}}X_{t}\|$	$\displaystyle=\|{\mathbb{E}}X_{t}-{\mathbb{E}}X_{{t_{n}}}\|\leq{\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|\leq\varepsilon+{\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|{\mathrm{I}}_{{\{\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon\}}}$
		$\displaystyle\leq\varepsilon+({\mathbb{E}}\|X_{t}-X_{{t_{n}}}\|^{2})^{{1/2}}{\mathbb{P}}(\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon)^{{1/2}}$
		$\displaystyle\leq\varepsilon+M{\mathbb{P}}(\|X_{t}-X_{{t_{n}}}\|\geq\varepsilon)^{{1/2}}\leq 2\varepsilon$