Zagadnienia
12. Dalsze własności całki stochastycznej
Podczas tego wykładu wykażemy szereg ważnych własności całki stochastycznej, które pozwolą nam później udowodnić wzór Itô.
12.1. Zbieżność zmajoryzowana dla całek stochastycznych
Zacznijmy od wersji stochastycznej twierdzenia Lebesgue'a o zbieżności zmajoryzowanej.
Twierdzenie 12.1
Załóżmy, że ![]() oraz
oraz ![]() są procesami
prognozowalnymi takimi, że
są procesami
prognozowalnymi takimi, że ![]() dla wszystkich
dla wszystkich
![]() . Jeśli dla wszystkich
. Jeśli dla wszystkich ![]() i
i ![]() ,
, ![]() dla pewnego procesu
dla pewnego procesu ![]() ,
to
,
to ![]() oraz
oraz
Proces ![]() jest prognozowalny jako granica procesów prognozowalnych. Ponadto dla
jest prognozowalny jako granica procesów prognozowalnych. Ponadto dla ![]() ,
,
więc ![]() . Bez straty ogólności możemy też założyć, że
. Bez straty ogólności możemy też założyć, że ![]() .
.
Niech ![]() takie, że
takie, że ![]() oraz
oraz
![]() . Ponieważ
. Ponieważ
![]() , więc
, więc
![]() . Z twierdzenia Lebesgue'a o zbieżności
zmajoryzowanej łatwo wykazać, że
. Z twierdzenia Lebesgue'a o zbieżności
zmajoryzowanej łatwo wykazać, że ![]() w
w ![]() . Stąd dla ustalonego
. Stąd dla ustalonego ![]() ,
,
czyli
Zbieżność w ![]() implikuje zbieżność według prawdopodobieństwa, by zakończyć dowód
wystarczy skorzystać z Lematu 11.1.
implikuje zbieżność według prawdopodobieństwa, by zakończyć dowód
wystarczy skorzystać z Lematu 11.1.
12.2. Całkowanie przez podstawienie
Definicja 12.1
Mówimy, że proces ![]() jest lokalnie ograniczony, jeśli istnieją momenty zatrzymania
jest lokalnie ograniczony, jeśli istnieją momenty zatrzymania
![]() takie, że procesy
takie, że procesy ![]() są ograniczone.
są ograniczone.
Uwaga 12.1
Każdy proces ciągły, adaptowalny jest lokalnie ograniczony.
Kolejne twierdzenie podaje wzór na całkowanie przez podstawienie.
Twierdzenie 12.2
a) Załóżmy, że ![]() ,
, ![]() ,
, ![]() jest procesem
prognozowalnym ograniczonym
oraz
jest procesem
prognozowalnym ograniczonym
oraz ![]() . Wówczas
. Wówczas ![]() oraz
oraz
![]() .
.
b)Załóżmy, że ![]() ,
, ![]() ,
, ![]() jest
procesem prognozowalnym lokalnie
ograniczonym oraz
jest
procesem prognozowalnym lokalnie
ograniczonym oraz ![]() . Wówczas
. Wówczas ![]() oraz
oraz
![]() .
.
a) Załóżmy wpierw, że ![]() jest procesem elementarnym postaci
jest procesem elementarnym postaci
![Y=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{j=0}}^{{n-1}}\xi _{j}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}},](wyklady/was/mi/mi1780.png) |
gdzie ![]() , zaś
, zaś ![]() są ograniczonymi zmiennymi
są ograniczonymi zmiennymi ![]() -mierzalnymi.
Wówczas
-mierzalnymi.
Wówczas
![\displaystyle=\sum _{{j}}\xi _{j}\Big(\int _{{0}}^{t}{\mathrm{I}}_{{[0,t_{{j+1}}]}}XdN-\int _{{0}}^{t}{\mathrm{I}}_{{[0,t_{j}]}}XdN\Big)](wyklady/was/mi/mi1658.png) |
|||
![\displaystyle=\sum _{{j}}\xi _{j}\int _{{0}}^{t}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}XdN=\sum _{{j}}\int _{{0}}^{t}\xi _{j}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}XdN](wyklady/was/mi/mi1747.png) |
|||
![\displaystyle=\int _{{0}}^{t}\sum _{j}\xi _{j}{\mathrm{I}}_{{(t_{j},t_{{j+1}}]}}XdN=\int _{0}^{t}YXdN.](wyklady/was/mi/mi1709.png) |
Jeśli ![]() jest dowolnym ograniczonym procesem prognozowalnym, to
jest dowolnym ograniczonym procesem prognozowalnym, to
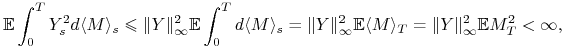 |
więc ![]() . Nietrudno też sprawdzić, że
. Nietrudno też sprawdzić, że ![]() .
Możemy znaleźć procesy elementarne
.
Możemy znaleźć procesy elementarne ![]() zbieżne do
zbieżne do ![]() w
w ![]() , co więcej możemy założyć, że
, co więcej możemy założyć, że ![]() .
Zauważmy, że
.
Zauważmy, że
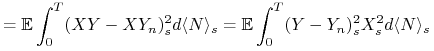 |
|||
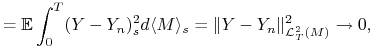 |
więc ![]() w
w ![]() . Stąd dla
. Stąd dla ![]() ,
,
b) Mamy ![]() , zatem
rozpatrując
, zatem
rozpatrując ![]() zamiast
zamiast ![]() możemy zakładać,że
możemy zakładać,że ![]() .
Niech
.
Niech ![]() takie, że
takie, że ![]() jest ograniczone,
jest ograniczone, ![]() oraz
oraz ![]() . Zauważmy, że
. Zauważmy, że
zatem na mocy części a),
Biorąc ![]() dostajemy tezę.
dostajemy tezę.
12.3. Całkowanie przez części
Sformułujemy teraz pierwsze twierdzenie o całkowaniu przez części.
Twierdzenie 12.3
Niech ![]() , wówczas
, wówczas
| (12.1) |
Stosując twierdzenie do ![]() dostajemy natychmiast.
dostajemy natychmiast.
Wniosek 12.1
Jeśli ![]() , to
, to
Wniosek 12.2
Niech ![]() ,
, ![]() oraz
oraz ![]() , wówczas
, wówczas
Dowód Twierdzenia 12.3
Całki ![]() i
i ![]() są dobrze określone, gdyż procesy
są dobrze określone, gdyż procesy ![]() i
i ![]() są ciągłe,
zatem lokalnie ograniczone.
są ciągłe,
zatem lokalnie ograniczone.
Możemy założyć, iż ![]() , gdyż
, gdyż ![]() ,
,
zatem
Wystarczy udowodnić, że teza zachodzi dla ![]() , tzn.
, tzn.
| (12.2) |
Jeśli bowiem zastosujemy (12.2) dla ![]() i
i ![]() , odejmiemy stronami i podzielimy
przez 4, to dostaniemy (12.1).
, odejmiemy stronami i podzielimy
przez 4, to dostaniemy (12.1).
Wiemy (zob. Uwaga 11.1), że (12.2) zachodzi przy dodatkowym założeniu
ograniczoności ![]() .
W ogólnym przypadku określamy
.
W ogólnym przypadku określamy
wtedy ![]() . Ponadto
. Ponadto ![]() jest ograniczonym martyngałem lokalnym, zatem
ograniczonym martyngałem, więc
jest ograniczonym martyngałem lokalnym, zatem
ograniczonym martyngałem, więc
Przechodząc z ![]() dostajemy (12.2).
dostajemy (12.2).
Definicja 12.2
Przez ![]() oznaczamy procesy ciągłe, adaptowalne, których trajektorie mają
wahanie skończone na każdym przedziale
oznaczamy procesy ciągłe, adaptowalne, których trajektorie mają
wahanie skończone na każdym przedziale ![]() dla
dla ![]() .
.
Udowodnimy teraz kolejne twierdzenie o całkowaniu przez części.
Stwierdzenie 12.1
Załóżmy, że ![]() , wówczas
, wówczas
Jak w dowodzie Twierdzenia 12.3 możemy założyć, że ![]() .
.
Załóżmy wpierw, że ![]() i
i ![]() są ograniczone. Zauważmy, że
są ograniczone. Zauważmy, że
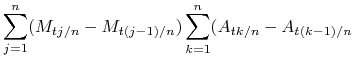 |
|||
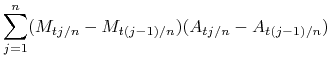 |
|||
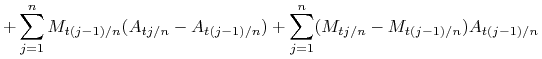 |
|||
Składnik ![]() dąży prawie na pewno do
dąży prawie na pewno do ![]() (definicja całki Riemanna-Stieltjesa).
Nietrudno sprawdzić, że procesy elementarne
(definicja całki Riemanna-Stieltjesa).
Nietrudno sprawdzić, że procesy elementarne
![A_{{n}}=\sum _{{j=1}}^{n}A_{{t(j-1)/n}}{\mathrm{I}}_{{(t(j-1)/n,tj/n]}}](wyklady/was/mi/mi1640.png) |
zbiegają w ![]() do
do ![]() , stąd
, stąd ![]() zbiega w
zbiega w ![]() do
do ![]() .
Zauważmy też, że
.
Zauważmy też, że
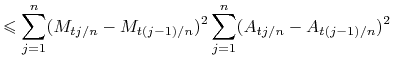 |
|||
![\displaystyle\leq\sum _{{j=1}}^{n}(M_{{tj/n}}-M_{{t(j-1)/n}})^{2}\sup _{{1\leq j\leq n}}|A_{{tj/n}}-A_{{t(j-1)/n}}|{\rm Wah}_{{[0,t]}}(A).](wyklady/was/mi/mi1755.png) |
Pierwszy czynnik powyżej dąży do ![]() w
w ![]() (w szczególności jest więc
ograniczony w
(w szczególności jest więc
ograniczony w ![]() ), drugi zaś dąży do zera p.n. (proces
), drugi zaś dąży do zera p.n. (proces ![]() jest ciągły),
stąd
jest ciągły),
stąd ![]() dąży do
dąży do ![]() według prawdopodobieństwa. Zatem
według prawdopodobieństwa. Zatem
Jeśli ![]() i
i ![]() nie są ograniczone, to określamy
nie są ograniczone, to określamy
Mamy ![]() ,
, ![]() , więc z poprzednio rozważonego
przypadku
, więc z poprzednio rozważonego
przypadku
przechodząc z ![]() dostajemy tezę.
dostajemy tezę.
Ostatnie twierdzenie o całkowaniu przez części jest nietrudną konsekwencją definicji całki Riemanna-Stieltjesa.
Stwierdzenie 12.2
Załóżmy, że ![]() , wówczas
, wówczas
12.4. Ciągłe semimartyngały
Definicja 12.3
Proces ![]() nazywamy ciągłym semimartyngałem, jeśli da się przedstawić
w postaci
nazywamy ciągłym semimartyngałem, jeśli da się przedstawić
w postaci ![]() , gdzie
, gdzie ![]() jest zmienną
jest zmienną ![]() -mierzalna,
-mierzalna, ![]() ,
,
![]() oraz
oraz ![]() .
.
Uwaga 12.2
Rozkład semimartyngału jest jednoznaczny (modulo procesy nieodróżnialne).
Jeśli ![]() , to
, to ![]() jest ciągłym martyngałem lokalnym, startującym
z zera o ograniczonym wahaniu na
jest ciągłym martyngałem lokalnym, startującym
z zera o ograniczonym wahaniu na ![]() dla
dla ![]() , zatem jest stale równy 0.
, zatem jest stale równy 0.
Przykład 12.1
Proces Itô, tzn. proces postaci ![]() , gdzie
, gdzie ![]() ,
,
![]() prognozowalny taki, że
prognozowalny taki, że ![]() p.n. dla
p.n. dla ![]() jest semimartyngałem.
jest semimartyngałem.
Przykład 12.2
Z twierdzenia Dooba-Meyera wynika, że kwadrat martyngału jest semimartyngałem.
Definicja 12.4
Jeśli ![]() jest ciągłym semimartyngałem, to określamy
jest ciągłym semimartyngałem, to określamy ![]() ,
gdzie pierwsza całka to całka stochastyczna, a druga całka Stieltjesa.
,
gdzie pierwsza całka to całka stochastyczna, a druga całka Stieltjesa.
Twierdzenie 12.4
Jeśli ![]() oraz
oraz ![]() są ciągłymi semimartyngałami, to
są ciągłymi semimartyngałami, to
![]() też jest semimartyngałem oraz
też jest semimartyngałem oraz
Mamy
![]() i stosujemy twierdzenia o całkowaniu przez części
(Twierdzenie 12.3, Stwierdzenia 12.1 i 12.2).
i stosujemy twierdzenia o całkowaniu przez części
(Twierdzenie 12.3, Stwierdzenia 12.1 i 12.2).
Dla semimartyngałów wygodnie jest też wprowadzić następującą definicję:
Definicja 12.5
Jeśli ![]() ,
, ![]() są ciągłymi semimartyngałami, to przyjmujemy
są ciągłymi semimartyngałami, to przyjmujemy
![]() .
.
12.5. Zadania
Ćwiczenie 12.1
Udowodnij Stwierdzenie 12.2.
Ćwiczenie 12.2
Korzystając ze wzoru na całkowanie przez części przedstaw
![]() jako wyrażenie nie zawierające całek stochastycznych.
jako wyrażenie nie zawierające całek stochastycznych.
Ćwiczenie 12.3
Załóżmy, że ![]() jest procesem ciągłym, a
jest procesem ciągłym, a ![]() ciągłym martyngałem lokalnym. Wykaż, że
jeśli
ciągłym martyngałem lokalnym. Wykaż, że
jeśli ![]() ,
,
![]() jest ciągiem podziałów
jest ciągiem podziałów ![]() takim, że
takim, że ![]() oraz
oraz
![]() , to
, to
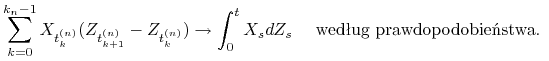 |
Ćwiczenie 12.4
Niech ![]() będzie ciągiem podziałów
będzie ciągiem podziałów ![]() takim, że
takim, że ![]() oraz
oraz
![]() . Wykaż, że dla dowolnych ciągłych semimartyngałów
. Wykaż, że dla dowolnych ciągłych semimartyngałów ![]() i
i ![]() ,
,
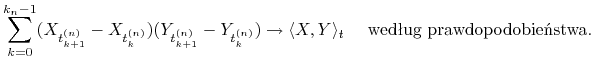 |




