Zagadnienia

11.1 Podstawowe definicje. Przykłady
11.2 Podział (Imputacja), Rdzeń
11.3 Rdzeń dla gier zrównoważonych

11. Gry Koalicyjne I

11.1. Podstawowe definicje. Przykłady

Używa się też nazw: Gry w postaci koalicyjnej, Gry kooperacyjne (Coalitional Games, Games in coalitional form, Cooperative games). Będziemy używali skrótu GK lub CG.

Są to n-osobowe gry w których gracze mogą tworzyć koalicje–podzbiory zbioru wszystkich n graczy. Każdej koalicji przypiszemy wartość. Będziemy żądać by każdy uczestnik koalicji miał wypłatę nie mniejszą niz gdyby nie brał udziału w koalicji. Podstawowym zagadnieniem będzie podział wypłaty (wartości) tzw. wielkiej koalicji pomiędzy wszystkich jej członków. Taki podział będzie utożsamiany z wynikiem, rozwiązaniem gry. Będziemy w szczególnosci poszukiwać podziałów mających własności równowagi, analogicznie do równowagi w grach strategicznych i ekstensywnych. Będziemy wymagać by równowaga miała pewne własności stabilności, analogicznie jak w przypadku RN, gdzie realizowała się w postaci optymalności wypłat przy ustalonych strategiach przeciwników.

Graczami mogą być osoby, grupy osób, firmy, zwiazki zawodowe, miasta, państwa, elementy projektów gospodarczych, naukowych, składniki produkcji itp.

Okazuje się że jest wiele koncepcji równowagi w grach koalicyjnych, nie ma jednej powszechnie uznanej, tak jak w grach strategicznych. Omówimy podstawowe: rdzeń, wartość Shapley'a, nukleous, a w dalszym rozdziałach rozwiązanie przetargowe Nasha. Krótko wzmiankujemy zbiory stabilne i rozwiązanie przetargu Kalai'a-Smorodinsky'ego.

Definicja 11.3 (Gra koalicyjna z wypłatami ubocznymi)

Gra koalicyjna z wypłatami ubocznymi jest to para $<N,v>$ , gdzie $N=\{ 1,...n\}$ jest zbiorem graczy, a $v:2^{N}\rightarrow R$ , zwana funkcją charakterystyczną gry, spełnia warunek $v(\emptyset)=0$ .

Definicja 11.4

Koalicja jest to dowolny podzbiór $S\in N$ . $N$ nazywamy wielką koalicją. Liczbę $v(S)$ nazywamy wartościa lub siłą koalicji $S$ .

Liczba $v(S)$ jest wypłatą jaką może uzyskać $S$ niezależnie od działań, akcji, koalicji pozostałych graczy. Zakładamy że istnieje medium–np. pieniądze, które ma jednakowa wartość dla wszystkich graczy i które gracze moga wymieniać bez ograniczeń między sobą–dopuszczamy wypłaty uboczne (transferable utilities, side payments).

Na ogół będziemy rozważać gry superaddytywne, czyli takie w których wartość sumy dwóch rozłącznych koalicji jest nie mniejsza niż suma ich wartości: łączenie się koalicji jest opłacalne (dokładniej–nie jest nieopłacalne). Jeżeli nie będzie explicite powiedziane inaczej, będziemy w dalszym ciągu zakładać superaddytywność GK.

Definicja 11.5

GK jest superaddytywna jeżeli

$S,T\in 2^{N}:\ S\cap T=\emptyset\Rightarrow v(S\cup T)\ge v(S)+v(T).$

Przykład 11.5

Zagadnienie bankructwa. Niech $N$ –zbiór wierzycieli (creditors, obligees), $d_{i}$ –wierzytelność (credibility) gracza $i$ , $M<\sum _{{i\in N}}d_{i}$ –masa upadłościowa, $v_{1}(S):=max\{ 0,M-\sum _{{i\notin S}}d_{i}\}$ –funkcja określająca ile zostałoby koalicji $S$ po spłaceniu wszystkich graczy spoza $S$ , $v_{2}(S):=min\{ M,\sum _{{i\in S}}d_{i}\}$ –funkcja określająca ile może uzyskać koalicja $S$ jeśli pierwsza i bez uwzględniania innych chce zrealizować swoją wierzytelność. $<N,v_{1}>$ jest superaddytywna, $<N,v_{2}>$ nie.

Liczbę $v(S)$ nazywamy łączną wypłatą wszystkich graczy w $S$ . Poszukujemy formalizacji pytania i odpowiedzi na pytanie jakie koalicje powinny zostać utworzone i jak podzielić $v(S)$ pomiędzy uczestników koalicji $S$ . $v(S)$ jest wypłatą którą może łącznie uzyskać $S$ , bez względu na to co zrobią gracze spoza $S$ .

Na mocy superaddytywności wartość $v(N)$ jest nie mniejsza niż suma wszystkich wartości uzyskanych przez dowolny rozłączny zbiór koalicji które moga utworzyć gracze.

Będziemy zakładać że gracze utworzą wielką koalicję, a więc łacznie uzyskają $v(N)$ .

Przykład 11.6 (Bankructwo (The Bankruptcy Game))

Firma która zbankrutowała jest dłużna trzem wierzycielom A, B, C nastepujace sumy: A 10, B 20, C 30. Wartość bankruta to 36. Zdefiniujemy wartość każdej koalicji $S$ jako sumę jaką może uzyskać gdy wszyscy gracze z $\bar{S}:=N\backslash S$ otrzymają całą sumę która żądają, a zero wpp., i.e. gdy $\bar{S}$ żąda 36 lub więcej. Tak więc (zauważmy że własność superaddytywności jest spełniona):

$v(A)=v(B)=0,\ v(C)=6,\ v(A\cup B)=6,\ v(A\cup C)=16,\ v(B\cup C)=26,\ v(N)=36$

(11.5)

Możemy jednakże inaczej zdefiniować wartość każdej koalicji $S$ , jako sumę jaką dostaje przy umowie ”pierwszy bierze wszystko” (”the first takes all”): koalicja $S$ uzyskuje sumę wszystkich wierzytelności żądań czlonków koalicji $S$ , lub 36 jeśli ta suma jest mie mniejsza niż 36 (superaddytywność nie zachodzi):

$v(A)=10,\ v(B)=20,\ v(C)=30,\ v(A\cup B)=30,\ v(A\cup C)=36,\ v(B\cup C)=36,\ v(N)=36.$

(11.6)

Oto inna funkcja charakterystyczna (potrzeba conajmniej dwóch wierzycieli aby odzyskać ich dług):

$v(A)=v(B)=v(C)=0,\ v(A\cup B)=30,\ v(A\cup C)=30,\ v(B\cup C)=36,\ v(N)=36.$

(11.7)

Przykład 11.7

$N=\{ Parlament\equiv P,Senat\equiv S,Prezydent\equiv Pr\}.$ Niech $M_{S}\subset S$ oznacza większość w koalicji $S$ : $|M_{S}|\ge\big[\frac{1}{2}|S|+1\big].$ GK $<N,v>$ zdefiniowana poniżej jest superaddytywna.

$\displaystyle v(S)=\left\{\begin{array}[]{ll}1,&\mbox{gdy S ma większość w P, S i Pr, lub conajmniej 2/3 w P i S}\\ 0,&wpp.\end{array}\right.$

(11.8)

11.2. Podział (Imputacja), Rdzeń

Wprowadzamy w GK dodatkową strukturę, która pozwala na zdefiniowanie rozwiązania i stabilności. GK z taką strukturą to GK z wypłatami ubocznymi (CG with transfer utilities, CGwTU).

Zakładamy że gracze tworza wielką koalicję. Ma ona wartość $v(N)$ . Będziemy chcieli podzielić $v(N)$ pomiędzy $n$ graczy.

Definicja 11.13

Wektor $x=(x_{1},x_{2},...,x_{n})\in\Re^{n}$ nazywamy wektorem wypłat $<N,v>$ .

Wektor wypłat $x$ nazywamy racjonalnym grupowo (lub alokacją) jeżeli

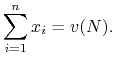$\sum _{{i=1}}^{{n}}x_{i}=v(N).$

Wektor wypłat $x$ nazywamy racjonalnym indywidualnie jeżeli

$x_{i}\ge v(\{ i\})\ \ \forall i=1,...,n.$

Wektor wypłat $x$ nazywamy racjonalnym koalicyjnie jeżeli

$\forall S\ \sum _{{j\in S}}\ x_{j}\ge v(S).$

Racjonalność grupowa oznacza efektywność wykorzystania wartości wielkiej koalicji.

Racjonalność indywidualna–że żaden gracz nie zgodzi się na mniej niż gdyby utworzył koalicję jednoosobową.

Racjonalność koalicyjna oznacza stabilność, patrz niżej.

Definicja 11.14 (Podział (Imputacja))

Wektor wypłat $x$ nazywamy podziałem (imputacją) jeżeli jest grupowo i indywidualnie racjonalny.

Podział (imputacja) jest więc indywidualnie racjonalną alokacją.

Lemat 11.2

W superaddytywych GK zbiór podziałów jest niepusty.

Zdefiniujmy wektor wypłat:

$\displaystyle x_{i}=\left\{\begin{array}[]{ll}v(\{ i\}),&gdy\ \ i=1,...n-1\\ v(N)-\sum _{{j=1}}^{{n-1}}v(\{ j\}),&gdy\ \ i=n,\end{array}\right.$

(11.10)

Jest to podział, gdyż z superaddytywności $x_{n}\ge v(\{ n\})$ .

∎

Przykład 11.18

$N=\{ 1,2,3\},v(N)=5,v(1)=1,v(2)=1,v(3)=2,v(1\cup 2)=2,v(1\cup 3)=3,v(2\cup 3)=4.$ Zbiór podziałów: $\{ x:x_{1}+x_{2}+x_{3}=5,\ x_{1}\ge 1,x_{2}\ge 1,\ x_{3}\ge 2\}$ .

Definicja 11.15

Mówimy że podział $x=(x_{1},...,x_{n})$ jest stabilny jeżeli dla każdej koalicji $S$

$\sum _{{i\in S}}x_{i}\ge v(S).$

Wpp. mówimy że podział $x$ jest niestabilny.

Stabilność podziału oznacza że jest on koalicyjnie racjonalny.

Definicja 11.16 (Rdzeń)

Zbiór $C(v)\equiv C$ stabilnych podziałów nazywamy rdzeniem GK $<N,v>$ .

$C:=\{ x:\sum _{{i\in N}}x_{i}=v(N)\ \ \wedge\ \ \forall S\subset N\ \ \sum _{{i\in S}}x_{i}\ge v(S)\}$

Interpretacja: żaden podzbiór graczy z $N$ nie ma powodu aby opuścić wielką koalicję by otrzymać jako koalicja wyższą łączną wypłatę.

Rdzeń może się składać z wielu (w szczególności z continuum) punktów, może być też nieintuicyjny lub pusty. Ta ostatnia ”wada” powoduje że rdzeń nie może spełniać takiej roli w GK jak RN w GS. Istnieje jednakże ważna klasa GK, opisująca klasyczny modele rynku, dla której rdzeń jest niepusty. Są to tzw. gry zrównoważone, patrz niżej. W następnej części omówimy inną definicję rozwiązania (wartość Shapley'a) , która będzie zawsze istniała, i to dokładnie jedna. Z drugiej strony rdzeń ma definicyjną własność stabilności, która nie jest rozważana przy omawianiu indeksu Shapley'a.

Uwaga 11.2

Rdzeń, jako zbiór wektorów o współrzędnych spełniających nierówności nieostre, jest domkniety i wypukły.

Przykład 11.19

W grze Bankructwo (11.5) w jej 1–ym wariancie rdzeń ma postać

$C=\{(x_{1},x_{2},x_{3}):x_{1}+x_{2}+x_{3}=36,\\ x_{3}\le 30,\ x_{2}\le 20,\ 6\le x_{1}\le 10\}.$

Zauważmy że ”intuicyjnie sprawiedliwa” imputacja: podział proporcjonalny do długu, $(6,12,18)$ , należy do rdzenia.

Przykład 11.20 (Podział 1 $ )

$v(1,2,3)=1=v(1,2)=v(1,3)=v(2,3),\ \ v(1)=v(2)=v(3)=0.$ $C=\{ x:x_{1}+x_{2}+x_{3}=1,\ x_{i}\ge 0,\ \ x_{i}+x_{j}\ge 1,\ \ i,j=1,2,3,\ i\neq j\}=\emptyset$

Zauważmy że $C=\emptyset$ także dla $v(i,j)=a>2/3$ . To że rdzeń jest tu zbiorem pustym odpowiada brakowi ”stabilnego rozwiązania” gry–gracz który nie należy do koalicji w której są dwaj pozostali, może zawsze złożyć ”kontrpropozycję” dla jednego z nich.

Definicja 11.17

GK jest istotna jeżeli

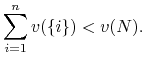$\sum _{{i=1}}^{{n}}v(\{ i\})<v(N).$

W przeciwnym przypadku, czyli gdy $\sum _{{i=1}}^{{n}}v(\{ i\})=v(N),$ GK jest nieistotna. (superaddytywność wyklucza przeciwną (ostrą) nierówność).

Wniosek 11.3

GK jest nieistotna $\Rightarrow$ jedynym podziałem jest $x_{i}=v(\{ i\}),\ i=1,...n$ , oraz $\forall S\subset N\ v(S)=\sum _{{i\in S}}v(\{ i\}).$

Definicja 11.18

GK jest grą o stałej sumie jeżeli

$\forall S\subset N\quad v(S)+v(\bar{S})=v(N).$

GK jest grą o sumie zero jeżeli $v(N)=0$ .

Twierdzenie 11.3

Rdzeń $C(v)$ istotnej GK o stałej sumie jest pusty.

Niech $x$ będzie dowolnym podziałem. Mamy $\sum _{{i=1}}^{{n}}v(\{ i\})<v(N)$ (istotność), a więc $\exists k:x_{k}>v(\{ k\})$ [wpp. $v(N)=\sum _{{i=1}}^{{n}}x_{i}\le\sum _{{i=1}}^{{N}}v(\{ i\})<v(N)$ ]. Ponieważ GK jest grą o stałej sumie, więc $v(N-\{ k\})+v(\{ k\})=v(N)$ . Tak więc dla koalicji $S:=N-\{ k\}$

$\sum _{{i\neq k}}x_{i}=\sum _{{i\in N}}x_{i}-x_{k}<v(N)-v(\{ k\})=v(N-\{ k\})=v(S),$

a więc $x\notin C(v)$ .

∎

Przykład 11.21

Gra Właściciel i Pracownicy

Właściciel $w$ i $m$ pracowników: $1\le m\le p:=|P|$ wytwarza $f(m)$ produktu, gdzie $P$ jest zbiorem wszystkich pracowników. Zakładamy że funkcja $f:\Re^{+}\rightarrow\Re^{+}$ jest wklęsła, niemalejąca, oraz $f(0)=0$ . Oznaczmy $N=\{ w\}\cup P$ - zbiór wszystkich graczy. Definujemy funkcję charakterystyczną

$\displaystyle v(S)=\left\{\begin{array}[]{ll}f(|S\cap P|),&gdy\ \ w\in S,\\ 0,&wpp.\end{array}\right.$

(11.11)

Oznaczmy $x=(x_{0},x_{1},...,x_{p})$ –wektor wypłat GK $<N,v>$ , gdzie $x_{0}$ jest wypłatą właściciela, $x_{1},...,x_{p}$ – wypłatami pracowników.

Stwierdzenie 11.1

Rdzeń Gry Właściciel i Pracownicy ma postać:

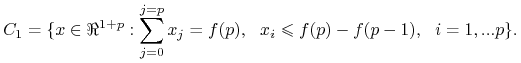$C_{1}=\{ x\in\Re^{{1+p}}:\sum _{{j=0}}^{{j=p}}x_{j}=f(p),\ \ x_{i}\le f(p)-f(p-1),\ \ i=1,...p\}.$

Z definicji rdzeń to zbiór $C=\{(x_{0},...,x_{p})\in\Re^{{p+1}}\}$ takich że:

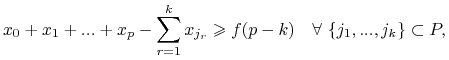$x_{0}+x_{1}+...+x_{p}-\sum _{{r=1}}^{k}x_{{j_{r}}}\ge f(p-k)\ \ \ \forall\ \{ j_{1},...,j_{k}\}\subset P,$

$x_{0}+x_{1}+...+x_{p}=f(p),$

gdzie pierwszy zestaw równań to warunki na rdzeń dla koalicji bez $1\le k\le p-1$ pracowników. Kombinując je z ostatnim równaniem mamy

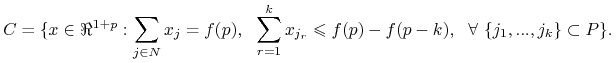$C=\{ x\in\Re^{{1+p}}:\sum _{{j\in N}}x_{j}=f(p),\ \ \sum _{{r=1}}^{k}x_{{j_{r}}}\le f(p)-f(p-k),\ \ \forall\ \{ j_{1},...,j_{k}\}\subset P\}.$

W szczególności dla koalicji bez jednego pracownika:

$x_{0}+x_{1}+...+x_{p}-x_{j}\ge f(p-1)\ \ \ \forall j=1,...,p,$

co implikuje $x_{j}\le f(p)-f(p-1),\ \ j=1,...,p.$ Pokażę że $C_{1}=C$ .

$C\subset C_{1}$ : Niech $x\in C$ . Pisząc nierówność z powyższych warunków na $C\$ $p$ razy, dla każdego z graczy (czyli za każdym razem dla $k=1$ ) otrzymujemy $p$ nierówności

$x_{{j}}\le f(p)-f(p-1),\ \ \forall\ j\in P,$

a zatem $x\in C_{1}$ .

$C_{1}\subset C$ : Niech $x\in C_{1}$ . Mamy

$\forall\ \{ j_{1},...,j_{k}\}\subset P\ \ x_{{j_{1}}}\le f(p)-f(p-1),\ ...,\ x_{{j_{k}}}\le f(p)-f(p-1)\}.$

Dodając te nierówności otrzymujemy

$x_{{j_{1}}}+x_{{j_{2}}}+...+x_{{j_{k}}}\le k[f(p)-f(p-1)]\le f(p)-f(p-k),$

czyli $x\in C$ . Drugą nierówność dowodzimy indukcyjnie. Dla $k=1$ mamy tożsamość. Niech nierówność będzie prawdziwa dla $k$ . Do jej obu stron dodajemy $f(p)-f(p-1)$ .

$(k+1)[f(p)-f(p-1)]\le 2f(p)-f(p-k)-f(p-1)\le f(p)-f(p-(k+1)).$

Druga nierówność wynika z wklęsłości $f$ , co widać przepisując ją w postaci

$f(p)-f(p-1)\le f(p-k)-f(p-(k+1)).$

∎

Przykład 11.22

Gra Rynek Rękawiczek (The Glove Market)

$m$ graczy ma po 1 lewej rękawiczce każdy, $n$ innych graczy – po 1 prawej, $\ m<n$ . Oznaczamy $M,N$ – zbiory tych graczy. Definiujemy funkcję charakterystyczną

$v(S)=min\{|S\cap M|,|S\cap N|\}.$

$v(S)$ jest liczbą par $(l,p)$ w koalicji $S$ . W szczególności $v(M\cup N)=m.$ Rdzeń GK jest jednoelementowy:

$C=\{(x_{1},...,x_{m},x_{{m+1}},...,x_{{m+n}}):x_{i}=1\ if\ i\in M,\ x_{i}=0\ if\ i\in N\}.$

$\$

1. Łatwo sprawdzić że zdefiniowany punkt należy do rdzenia.

2. Niech któryś z ”prawych” graczy, np. o numerze $j\ge m+1$ , ma w $C$ wypłatę $x_{j}>0$ . Wtedy dla koalicji $S:=M\cup N\backslash\{ j\}$ mamy

$\sum _{{i\in S}}x_{i}=\sum _{{i\in M\cup N}}x_{i}-x_{j}=v(M\cup N)-x_{j}<v(M\cup N).$

Ale $v(S)=v(M\cup N)$ –liczba par rekawiczek w wielkiej koalicji. Tak więc $\sum _{{i\in S}}x_{i}<v(S)$ , czyli $x\notin C$ .

3. Niech któryś z ”lewych” graczy, o numerze $j\le m$ , ma w $C$ wypłatę $x_{j}<1$ . Rozważmy koalicję złożoną z $j$ i jednego z ”prawych”, o numerze $r$ i wypłacie $x_{r}$ . Musi więc być $x_{j}+x_{r}\ge 1$ (bo $v(rl)=1$ ). Ponieważ $x_{j}<1$ więc $x_{r}>0,$ sprzeczność, bo poprzednio wykazaliśmy że w rdzeniu wszystkie $x_{r}$ sa zerami. Tak więc dla ”lewych” $x_{j}\ge 1$ . Ponieważ $\sum _{{j\in M\cup N}}x_{j}=v(M\cup N)=m=\sum _{{j\in M}}x_{j},$ więc dla ”lewych” zachodzi $x_{j}=1$ .

∎

Rdzeń tej gry jest ”nieintuicyjny”. Strona będąca ”nawet w minimalnym nadmiarze” ma w $C$ wypłaty zerowe–wartość rynkowa prawych rękawiczek jest zerowa. Okazuje się że drugie ważne pojęcie rozwiązania GK: wartość Shapley'a, nie ma tego typu ”bulwersującej” własności. Suma wartości Shapley'a (patrz następny wykład) dla $m=10^{6},n=10^{6}+1$ wynosi $0,500428$ dla właścicieli lewych rękawiczek, $0,499572$ dla prawych.

11.3. Rdzeń dla gier zrównoważonych

Istnieje ważna klasa GK, mająca zastosowanie w ekonomii matematycznej (klasyczny model rynku), dla której rdzeń jest niepusty. Są to tzw. gry zrównoważone (balanced games).